文献情報
- タイトル:Nonnegative/Binary matrix factorization for image classification using quantum annealing
- 著者:Hinako Asaoka & Kazue Kudo
- 書誌情報:https://doi.org/10.1038/s41598-023-43729-z
概要
非負二値行列因子分解(NBMF)は、元々量子アニーリングを用いて学習される生成モデルとして提案された手法です。以前の研究ではNBMFを用いた顔画像の再構築といった課題が扱われてきました。しかし、NBMFを他の機械学習課題に応用したり、他の機械学習手法と比較したりする試みはほとんど行われていませんでした。そこで本論文ではNBMFの応用として多クラス画像分類モデルを提案し、手書き数字画像データの分類問題に対して、提案手法と古典的な機械学習手法を比較して、その有効性を評価しました。その結果、データ量、特徴数、エポック数が少ないという特定の条件下で、NBMFがニューラルネットワークなどの従来手法よりも高い分類精度を示すことが明らかになりました。さらに、量子アニーリングマシンを用いることで、学習にかかる計算時間を大幅に削減できることも示されました。これらの結果から、特定の条件下において、機械学習に量子アニーリング技術を活用することの有効性と利点が明らかとなりました。
背景
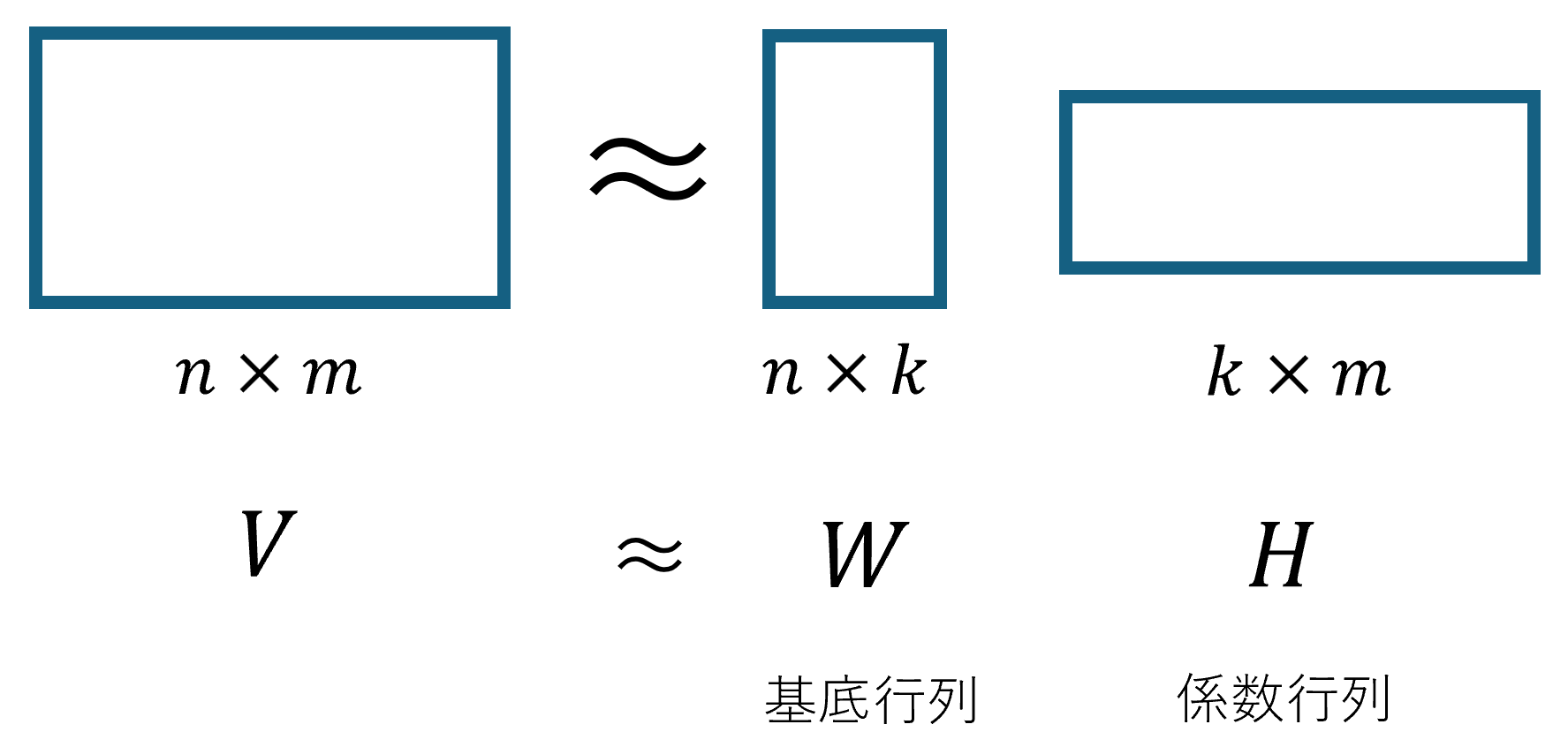
非負二値行列因子分解とは、あるデータを表す$n \times m$行列$V$を基底行列$W$と係数行列$H$に分解する手法です(図1)。基底行列とはデータの特徴を表す非負値の$n \times k$行列であり、列数$k$は抽出される特徴の数を表します。係数行列とは、元の行列を再構成する際に、基底行列のどの特徴を組み合わせるかを示す二値の$k \times m$行列です。
非負二値行列因子分解をD-Waveマシンに適用した研究として、顔画像の再構成を目的としたものがあります[1]。この研究の解説記事は本サイト内で公開されています[2]。以下では、非負二値行列因子分解を用いた顔画像の再構成について、その概要を簡単に説明します。顔画像の再構成において、入力データは$m$枚の顔画像です。1枚の画像の画素数を$n$とすると顔画像データは$n \times m$の行列$V$として表すことができます。この行列$V$を非負二値行列因子分解によって基底行列$W$と係数行列$H$に分解します。この分解によって、元の$m$枚の顔画像を、あらかじめ抽出された$k$枚の特徴的な顔画像の組み合わせとして表現することができます。イメージとしては、$m$人の顔を表す画像から共通する特徴を抽出して$k$枚の顔画像を作り、その$k$枚の顔画像の中から必要な特徴を選び出して足し合わせることで元の顔画像を再構成するというものです。[1]の論文における結果の一例を図2に示します。図の左上にある画像が元の顔画像(行列$V$に含まれる画像の1つ)であり、その下に示された画像が再構成された画像、すなわち基底行列$W$と係数行列$H$の積によって得られた画像です。右側に並んだ35枚の画像は、基底行列を構成する顔画像、すなわち基底行列$W$の各列に対応する画像です。この例では、緑枠で示された3枚の画像を組み合わせることで、元の顔画像が再構成されていることが分かります。
![[1]の論文に示されている結果の画像](/T-Wave/wp-content/uploads/2025/07/9ea7473ebcffdff615de0d5a04fb0f59-1.png)
https://doi.org/10.1371/journal.pone.0206653
次に、非負二値行列因子分解の具体的な手法について説明します。非負二値行列因子分解の目標は、与えられた行列$V$に対して、基底行列$W$と係数行列$H$の積との誤差が最小となるような$W$と$H$を求めることです。これは、以下の式で表される両辺の差を最小にすることを目指します。
$$
\tag{1}
V \approx W H
$$
(1)式で表される式の両辺の差を小さくするため、$W$と$H$をそれぞれ以下の式で交互に更新していきます。
$$
\tag{2}
W \coloneqq \arg\min_{X \in \mathbb{R}_{+n \times k}}
\bigl( \| V – X H \|_F + \alpha \| X \|_F \bigr)
$$
$$
\tag{3}
H \coloneqq \arg\min_{X \in \{0,1\}^{k \times m}}
\bigl\| V – W X \bigr\|_F
$$
ここで、(2)式と(3)式に現れる$\| \cdot \|_F$はフロベニウスノルムと呼ばれ、行列の全成分の二乗和の平方根を表します。
まず、(2)式を解くための射影勾配法について説明します。射影勾配法とは、解の値に制約がある場合に用いられる勾配法の一種です。通常の勾配法では、勾配と学習率に基づいて変数の値を調整し、最大値または最小値を求めます。この時の変数の更新式は以下のようになります。
$$
\tag{4}
x_{n+1} = x_n – \gamma \frac{df}{dx_n} \quad (\gamma: \text{学習率})
$$
ここで、変数に入る値に非負値などの制約があるとします。(4)式で求められた値が制約に違反する可能性があるため、これを防ぐために(4)式を以下の式のように修正します。今回は変数に対して非負制約がある場合を仮定します。
$$
\tag{5}
x_{n+1} = P\left[ x_n – \gamma \frac{df}{dx_n} \right] \quad (\gamma: \text{学習率})
$$
$$
\tag{6}
P\left[ x \right] =
\begin{cases}
0 & x < 0 \\
x & x \geq 0
\end{cases}
$$
(4)式で求められる値を射影することで、更新された変数は必ず制約を満たします。これが射影勾配法です。この射影勾配法を用いて(2)式を解くために、まず(2)式をベクトルの形で表します。(2)式について、$W$の行ベクトルを$x$の転置、$V$の行ベクトルを$v$の転置として、以下の損失関数を考えます。
$$
\tag{7}
f_W\left(\boldsymbol{x}\right) = \| \boldsymbol{v} – H^{\mathsf{T}} \boldsymbol{x} \|^2 + \alpha \| \boldsymbol{x} \|^2
$$
(7)式の右辺の第一項は(1)式の両辺の差を表し、第二項は正則化項と呼ばれ、$x$の値が大きくなりすぎないように設定されています。(7)式を最小化するような$x$を求めることで、(2)式の$W$を更新したことになります。(7)式の最小化に射影勾配法を用いるため、勾配を求めます。まず, 以下のように式変形を行います。
$$
\tag{8}
\begin{aligned}
f_W\left(\boldsymbol{x}\right)
&= \| \boldsymbol{v} – H^{\mathsf{T}} \boldsymbol{x} \|^2 + \alpha \| \boldsymbol{x} \|^2 \\
&= \bigl(\boldsymbol{v} – H^{\mathsf{T}} \boldsymbol{x}\bigr)^{\mathsf{T}} \bigl(\boldsymbol{v} – H^{\mathsf{T}} \boldsymbol{x}\bigr) + \alpha\, \boldsymbol{x}^{\mathsf{T}} \boldsymbol{x} \\
&= \boldsymbol{v}^{\mathsf{T}} \boldsymbol{v}
– \boldsymbol{v}^{\mathsf{T}} H^{\mathsf{T}} \boldsymbol{x}
– \bigl(H^{\mathsf{T}} \boldsymbol{x}\bigr)^{\mathsf{T}} \boldsymbol{v}
+ \bigl(H^{\mathsf{T}} \boldsymbol{x}\bigr)^{\mathsf{T}} \bigl(H^{\mathsf{T}} \boldsymbol{x}\bigr)
+ \alpha\, \boldsymbol{x}^{\mathsf{T}} \boldsymbol{x} \\
&= \boldsymbol{v}^{\mathsf{T}} \boldsymbol{v}
– 2 \boldsymbol{v}^{\mathsf{T}} H^{\mathsf{T}} \boldsymbol{x}
+ \boldsymbol{x}^{\mathsf{T}} H H^{\mathsf{T}} \boldsymbol{x}
+ \alpha\, \boldsymbol{x}^{\mathsf{T}} \boldsymbol{x}
\end{aligned}
$$
$$
\bigl(\because \bigl(H^{\mathsf{T}} \boldsymbol{x}\bigr)^{\mathsf{T}} = \boldsymbol{x}^{\mathsf{T}} H,\quad
\boldsymbol{x}^{\mathsf{T}} H \boldsymbol{v} = \boldsymbol{v}^{\mathsf{T}} H^{\mathsf{T}} \boldsymbol{x} \bigr)
$$
式(8)より勾配を求めると、以下のようになります。
$$
\tag{9}
\boldsymbol{\nabla} f_W
= – H \bigl( \boldsymbol{v} – H^{\mathsf{T}} \boldsymbol{x} \bigr) + \alpha \boldsymbol{x}
$$
$$
\bigl(
\because\
\boldsymbol{\nabla}_{\boldsymbol{x}}\, \boldsymbol{v}^{\mathsf{T}} \boldsymbol{v} = 0,\quad
\boldsymbol{\nabla}_{\boldsymbol{x}}\, \boldsymbol{a}^{\mathsf{T}} \boldsymbol{x} = \boldsymbol{a},\quad
\boldsymbol{\nabla}_{\boldsymbol{x}}\bigl(\boldsymbol{x}^{\mathsf{T}} A \boldsymbol{x}\bigr) = 2A \boldsymbol{x},\quad
\boldsymbol{\nabla}_{\boldsymbol{x}}\bigl(\boldsymbol{x}^{\mathsf{T}} \boldsymbol{x}\bigr) = 2\boldsymbol{x}
\bigr)
$$
この勾配から変数$x$についての更新式を求めますが、今回変数$x$に入る値には「0以上1以下の実数」という制約が設けられています。これは、後に扱う多クラス画像分類問題に用いられる画像がグレースケール画像であることに起因しています。このことを踏まえ、変数の値が0以上1以下となるような射影を考えて、$x$の更新式を以下のように定めます。
$$
\tag{10}
\boldsymbol{x}^{t+1} = P \left[ \boldsymbol{x}^{t} – \gamma_t \boldsymbol{\nabla} f_W \bigl( \boldsymbol{x}^t \bigl) \right]
$$
$$
\tag{11}
P\left[x\right] =
\begin{cases}
0 & x \leq 0 \\
x & 0 < x < 1 \\
1 & x \geq 1
\end{cases}
$$
このようにすることで、制約を満たしつつ変数$x$の更新を行うことができます。これらの式から射影勾配法を用いることで$W$の更新、すなわち(2)式を解くことが可能になります。
次に$H$の更新、すなわち(3)式を解くことを考えます。(3)式における変数である$X$は二値行列であるため、これは組み合わせ最適化問題として捉えられます。具体的には、(3)式はQUBO形式として表現でき、QUBO形式で表された問題はD-Waveマシンなどの量子アニーリングマシンを用いて解くことが可能です。QUBOは「Quadratic Unconstrained Binary Optimization(二次制約なし二値最適化)」の略で、以下の式で表される形式を指します。
$$
\tag{12}
QUBO \bigl( \boldsymbol{q} \bigl) = \sum_{i \leq j} Q_{ij} q_i q_j
$$
(3)式を(12)式のような形に変形するため、まず行列ではなくベクトルの形式で表現します。$H$と$V$の特定の列ベクトルをそれぞれ$q$,$v$とすると(3)式は以下のように変形できます。
$$
\tag{13}
\begin{aligned}
f_H \bigl( \boldsymbol{q} \bigr)
&= \sum_r \bigl( v_r – \sum_i W_{ri} q_i \bigr)^2 \\
&= \sum_r \Bigl\{ v_r^2 – 2 v_r \sum_i W_{ri} q_i + \bigl( \sum_i W_{ri} q_i \bigr)^2 \Bigr\}
\end{aligned}
$$
(13)式を以下の(14)式と(15)式を用いてさらに変形すると、(16)式が得られます。ただし、$v_r^2$は$q$に依存しない定数のため省略しました。
$$
\tag{14}
\begin{aligned}
\bigl( \sum_i W_{ri} q_i \bigr)^2
&= \sum_i \sum_j W_{ri} W_{rj} q_i q_j \\
&= \sum_{i < j} W_{ri} W_{rj} q_i q_j + \sum_{i > j} W_{ri} W_{rj} q_i q_j + \sum_{i = j} W_{ri}^2 q_i^2 \\
&= 2 \sum_{i < j} W_{ri} W_{rj} q_i q_j + \sum_i W_{ri}^2 q_i^2
\end{aligned}
$$
$$
\tag{15}
q_i^2 = q_i \quad \bigl( \because q_i \in \{ 0, 1 \} \bigr)
$$
$$
\tag{16}
f_H \bigl( \boldsymbol{q} \bigr)
= \sum_i \Bigl( \sum_r W_{ri} \bigl( W_{ri} – 2 v_r \bigr) \Bigr) q_i
+ 2 \sum_{i < j} \Bigl( \sum_r W_{ri} W_{rj} \Bigr) q_i q_j
$$
(16)式はQUBO形式であるため、$H$を更新するという問題を量子アニーリングで解けるようになります。
以上の定式化により、射影勾配法と量子アニーリングをそれぞれ用いて$W$と$H$を交互に更新していくことで、(1)式の両辺の誤差が小さい$W$と$H$を求めることができます。すなわち、元のデータ$V$を非負二値行列因子分解によって$W$と$H$に分解することが可能になります。
提案手法
本論文では、非負二値行列因子分解(NBMF)を用いて多クラス画像分類を行う方法を提案します。具体的には、画像分類モデルの学習をNBMFによって実現します。
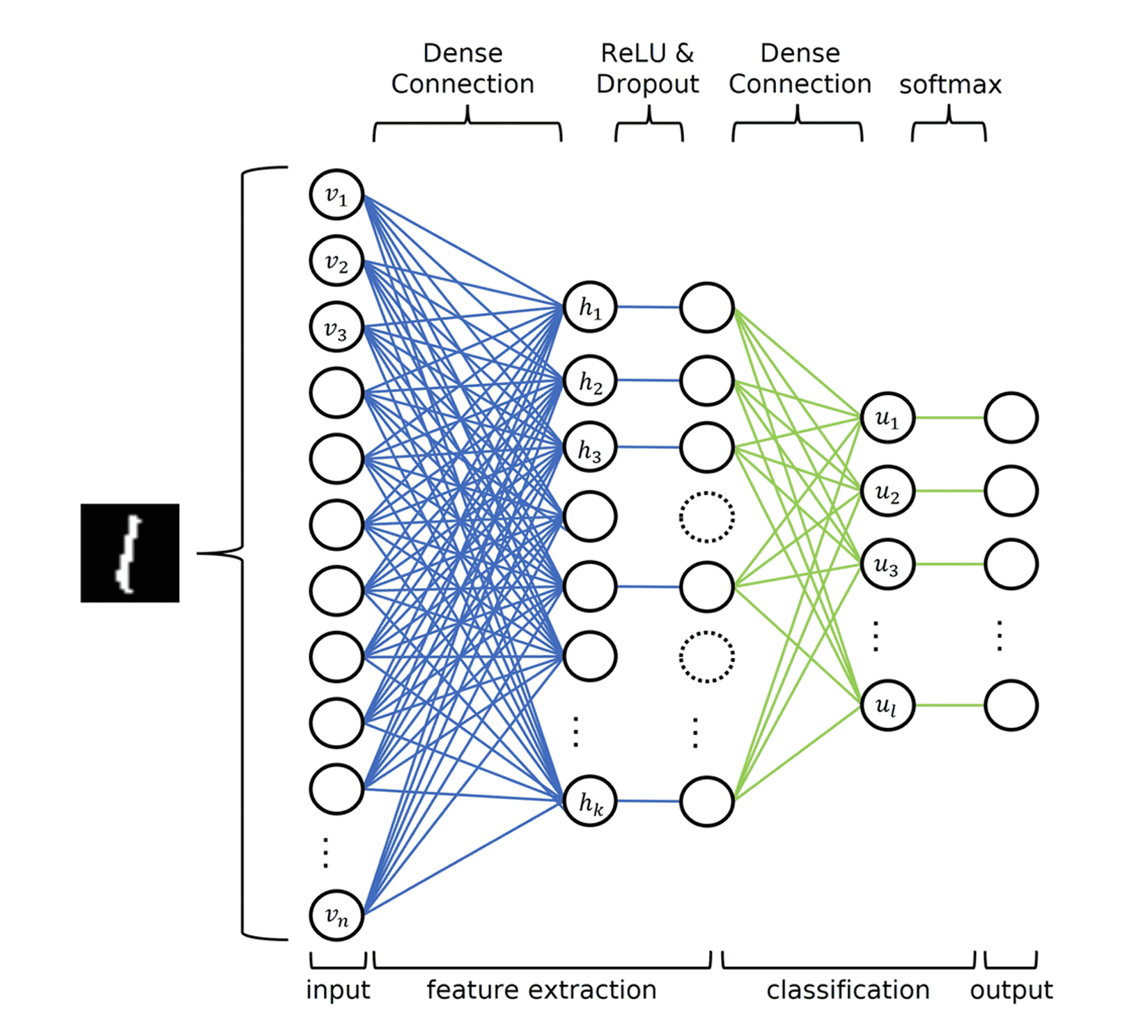
まず、画像分類モデルを全結合ニューラルネットワーク(FCNN)から定義します。FCNNは図3に示すように、入力層、隠れ層、出力層という構造を持っています。それぞれの層の役割は以下の通りです。
- 入力層:画像データなどの特徴量を表現します。
- 隠れ層:学習された特徴表現を表します。
- 出力層:分類結果を表します。
NBMFによる画像分類モデルではFCNNの入力層と出力層を組み合わせた構造をNBMFで実現します。つまり、NBMFにおける入力行列$V$に、FCNNの入力層と出力層にあたる画像データとクラス情報を与え、その行列$V$をNBMFによって分解することでモデルを学習します。
https://doi.org/10.1038/s41598-023-43729-z
ここで、行列$V$と、分解によって得られる$W$、$H$が表すものについて説明します。図4にNBMFによる学習の概要を示します。以下に、$V$と、$W$と$H$についての説明を示します。
- $V$:入力行列を表します。入力としては、画像データと、その画像のクラス情報が含まれます。
- $W$と$H$:$V$を分解した結果です。非負二値行列因子分解の説明でも述べた通り、$W$はデータの特徴を、$H$は$V$を構成する際に$W$のどの列を組み合わせるかを決定する係数を表します。
また、$W$は$W_1$と$W_2$の2つに分けられます。これは、それぞれが表す情報が異なるためです。後ほど、$W$に含まれる情報について詳しく説明しますが、以下では$W_1$と$W_2$のそれぞれについて簡単に説明します。
- $W_1$:画像の視覚的な特徴を表します。
- $W_2$:クラス情報の特徴を表します。すなわち、$W_2$は、同じ列の$W_1$が持つ視覚的情報を持つ画像が、どのクラスに属する傾向があるのかという情報を含んでいます。
次にそれぞれの行列の行数と列数を表す文字について説明します。
- $V$の行数および$W$の行数$(n+l)$:$n$は画像1枚の画素数、$l$はラベルの数を表します。
- $V$の列数および$H$の列数$m$:$m$は入力する画像の枚数を表します。
- $W$の列数および$H$の行数$k$:特徴次元数、すなわち入力画像をいくつの特徴によって表現するかを表します。
クラス情報の表現方法ですが、画像を表す列の末尾に、one-hotベクトルに一定の重み係数$g$を掛けたものを追加することで表現しています。例えば、手書き数字の分類で数字が10種類ある場合を考えます。このとき、10個の要素を持つ0ベクトルを用意し、クラス情報に基づいて該当する位置のみを$g$にすることで、それぞれのクラスを区別して表現できます。数字が「1」の画像であれば2番目の要素を$g$にし、それ以外を0にします。同様に、数字が「7」の画像であれば8番目の要素を$g$にし、それ以外を0にします。
以上のように入力データをWとHに分解することで、画像とそのクラスの情報を学習します。

https://doi.org/10.1038/s41598-023-43729-z
ここでは、非負二値行列因子分解(NBMF)によって学習された$W$を用いてテストデータを分類する方法を説明します。図5に分類方法の概要を示します。テストデータの分類は、学習済みの$W$行列を$W_1$と$W_2$に分けて使用し、以下の手順で行われます。
- テストデータ$V_{test}$を$W_1$を用いて分解し、$H_{test}$を得ます。
- $W_2$に$H_{test}$を乗算して、$U_{test}$を得ます。
- 得られた$U_{test}$にソフトマックス関数を適用し、最大の成分値を持つインデックスを予測されたクラスとします。

https://doi.org/10.1038/s41598-023-43729-z
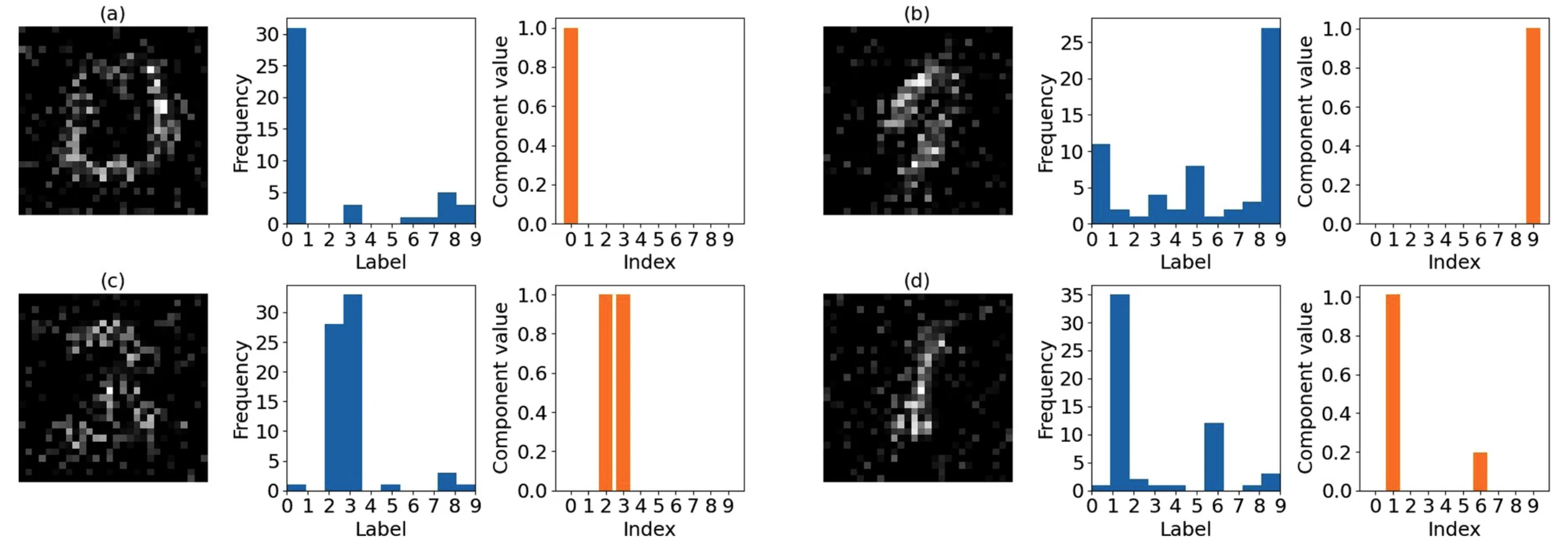
次に、$W$に含まれる情報について詳しく説明します。図6は、MNISTの手書き数字画像300枚を特徴数40という条件で学習させた際の$W$に含まれる情報の一部を示しています。図の(a)から(d)は$W_1$の列ベクトルが表す画像です。これらは、元の画像を表現するための「基底画像」のようなものだと考えられます。つまり、これらの画像の組み合わせによって、元の画像を再構成できるということです。また、図中のオレンジ色の棒グラフは、その画像に対応する$W_2$の列ベクトルの値を示しています。一方、青色のヒストグラムは、その画像がそれぞれの数字を再構成する際に用いられた回数を表しています。(a)の画像を見ると「0」に近いような画像となっているのが分かります。実際、ヒストグラムや棒グラフを見ると、「0」を再構成する際によく用いられていることが分かります。すなわち、(a)の画像では「0」の画像の特徴を学習しているということが分かります。同様に、(b)の画像では「9」の画像の特徴を、(c)の画像では「2」と「3」の画像の特徴を、(d)の画像では主に「1」の画像の特徴を学習していることが分かります。このように、$W_1$は視覚的な特徴の要素を、$W_2$はそれらの特徴がどのクラスに関連しているかの情報を学習しています。
https://doi.org/10.1038/s41598-023-43729-z
次に、本論文で新たに提案する$W$の更新方法について説明します。先行研究では勾配降下法を用いて$W$の更新を行っていましたが、この方法にはいくつか問題点がありました。具体的には、勾配が大きい場合にはパラメータの変化が大きくなりすぎたり、勾配が小さい場合にはパラメータの変化が小さくなりすぎたりし、局所解に陥りやすいという課題です。そこで本論文では、新たにRMSPropという手法を提案します。RMSPropは勾配降下法の一種で、勾配の大きさに応じてパラメータごとの学習率を自動で調整するものです。この方法を用いることで、勾配が激しく変動する場合であっても安定した更新が可能になります。
RMSPropの具体的な手法について説明します。RMSPropでは、関数の勾配に応じて$x$の更新幅を変化させるため、「勾配の二乗平均$h$」という概念を導入します。$h$を表す式を以下に示します。
$$
\tag{17}
h_i^{t+1} = \beta h_i^t + \bigl( 1 – \beta \bigr) g_i^2
$$
ここで、$\beta$は以前の情報をどれだけ残すかを表す定数で、$g$は勾配を表しています。(17)式は、時刻$t+1$における勾配の二乗平均が、時刻$t$までの勾配の二乗平均に$\beta$の重みをつけたものと、時刻$t$における勾配の二乗に$(1-\beta)$の重みをつけたものの和によって表現されることを意味します。これにより、勾配の二乗の移動平均を定義しています。この勾配の二乗平均を用いて、(10)式で表される$x$の更新式を以下のように書き換えます。
$$
\tag{18}
\boldsymbol{x}^{t+1}
= P \biggl[
\boldsymbol{x}^t
– \eta \frac{1}{\sqrt{\boldsymbol{h}^t + \epsilon}} \nabla f_W
\biggr]
$$
$\boldsymbol{x}$には制約がある状態を考えるため、RMSPropにおいても射影を考慮します。したがって、$P[ \cdot ]$の部分は(11)式と同様の内容になります。また, $\eta$は学習率、$\epsilon$は計算誤差を防ぐための小さな値です。このように(10)式の勾配の係数に$\frac{1}{\sqrt{\boldsymbol{h}^t + \epsilon}}$を乗算することで勾配が大きいときは更新の幅を小さく、逆に勾配が小さいときは更新の幅を大きくすることができます。
実験
本実験では、MNISTの手書き数字画像の分類問題を解決するため、以下の5つの手法を用いてその精度と計算時間を比較します。この際、学習データ数、特徴次元数、エポック数の3つをパラメータとして設定し、それぞれのパラメータについて実験を行いました。使用した手法は以下の通りです。
- 古典的機械学習手法:
- 全結合ニューラルネットワーク(FCNN)
- 非負値行列因子分解(NMF)
- アニーリング手法:
- D-Waveマシン
- Fixstars Amplify Annealing Engine(AE)
- シミュレーテッド・アニーリング(SA)
以下に、それぞれの手法について簡単に説明していきます。
-
- 全結合ニューラルネットワーク(FCNN)
FCNNは、入力層、隠れ層、出力層の前後でニューロンが接続されたネットワークです。入力層から隠れ層を通して出力層へ情報を伝播させることで特徴を学習します。隠れ層ではReLU関数によって活性化され、出力層はソフトマックス関数によって活性化されます。過学習を防ぐため、隠れ層には20%のランダムドロップアウトを設定しています。
-
- 非負値行列因子分解(NMF)
NMFは、非負二値行列因子分解(NBMF)とは異なり、係数行列$H$に二値制約は課されません。そのため、$H$行列の成分は二値ではなく、正の実数値となります。目的関数はNBMFと同様に行列$V$と$WH$の差を最小化することです。NMFでの$W$と$H$の更新には、乗法更新法[3]と座標降下法[4]を使用します。乗法更新法は、要素の更新に乗法および除法のみを用いることで非負性を担保する方法です。また、座標降下法は、一度にすべての変数を最適化するのではなく、更新する行列に大きく影響を与える一部の要素に絞って最適化していく手法です。
-
- D-Waveマシン
D-Waveマシンは、量子ビットを搭載した量子アニーリングマシンです。目的関数の最小化には、変数を量子ビットに埋め込む必要があります。本実験では、この埋め込み処理にD-Waveソフトウェア開発キット(SDK)に実装された自動関数を用いました。アニーリング結果の読み出し回数は50回とし、その中で目的関数が最も低い解を選択しました。
-
- Fixstar Amplify Annealing Engine(AE)
AEは、Fixstars社が開発したソフトウェアエンジンです。その仕組みは、SAを並列化したようなものです。本実験において、アニーリングスケジュールと温度の値はソルバーが自動的に決定し、アニーリング結果の読み出し時間は1000ミリ秒としました。
-
- シミュレーテッド・アニーリング(SA)
SAは量子揺らぎではなく熱揺らぎを用いて最適化を行うソルバーです。この熱揺らぎは、温度のパラメータによって制御されます。本実験ではSAの実装にPythonパッケージのPyQUBOを用いました。アニーリングスケジュールと温度の値はソルバーが自動的に決定し、アニーリング結果の読み出し回数は50回としました。
NBMFを用いたのはアニーリング手法の3つで、エポック数は10回としました。また、全結合ニューラルネットワークにおけるエポック数も10回としましたが、これでは本来の性能を十分に発揮できない可能性があるため、エポック数をパラメータとした実験も行いました。分類性能については、各分類モデルについて初期値をランダムに設定し、10エポック学習を3回行いました。そして、3回の試行それぞれの最高精度を記録し、その平均値を取りました。また、最終エポックでの交差エントロピー誤差も計算し、その平均値も取得しました。これら2種類の平均値をそれぞれ分類性能としています。
交差エントロピー誤差は、以下の式で表現される値です。
$$
\tag{19}
H\bigl(p, q\bigr)
= – \sum_{x} p\bigl(x\bigr) \log_e \bigl( q\bigl(x\bigr) \bigr)
$$
ただし、$p$は真の確率分布、$q$は推定した確率分布です。$p$と$q$の確率分布が似ているときに交差エントロピー誤差は小さくなり、似ていないときに大きくなります。今回、最終結果にソフトマックス関数を適用しているため、結果は確率分布のように扱うことができます。
最後に実験に用いたデータセットと各種定数の値を説明します。実験に用いたデータセットはMNISTです。MNISTは、サイズが$28 \times 28$のグレースケールの手書き数字画像で構成されています。MNISTには10クラスで合計6万枚の画像が含まれていますが、本実験ではこのデータセットからランダムに訓練用とテスト用の画像を選択しました。テスト用の画像の枚数は500枚で固定し、訓練用の枚数は実験ごとに変化させました。各種定数については以下の通り設定しました。
-
- $W$の更新時の正則化項:
$$
α=1.0×10^{(-4)}
$$
-
- RMSPropでの過去の情報への重み:
$$
β=0.99
$$
-
- 学習率:
$$
η=0.01
$$
-
- 計算誤差防止用の値:
$$
ϵ=1.0×10^{(-7)}
$$
-
- 入力行列$V$に追加する、クラス情報を表すone-hotベクトルへの係数:
$$
g=9
$$
結果
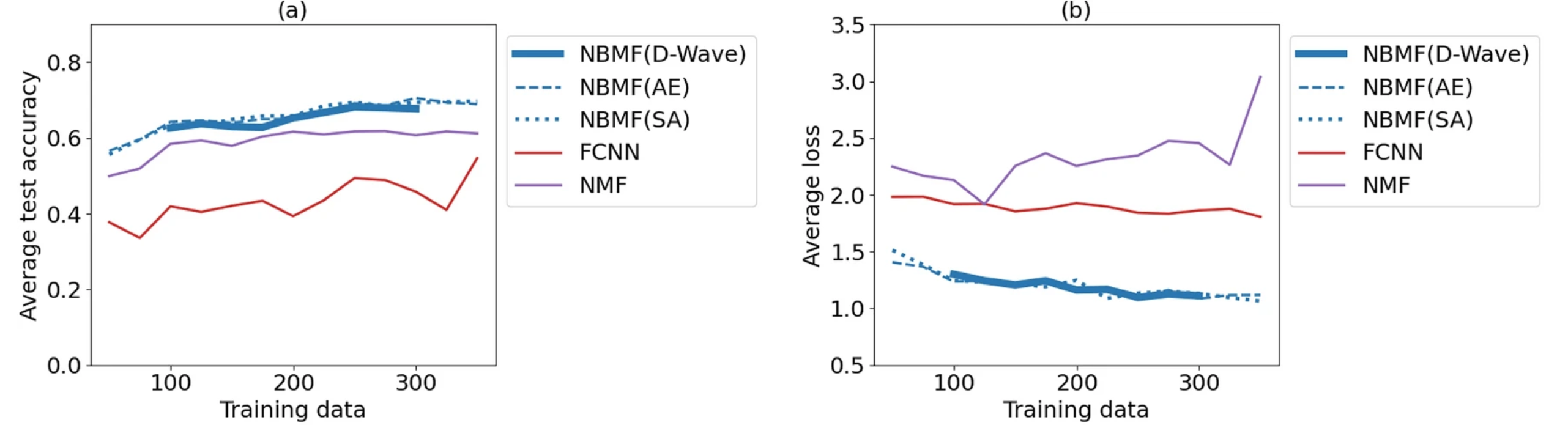
まず、学習データ数をパラメータとして変化させた場合の結果を図7に示します。この実験では、特徴数を40、エポック数を10と設定しました。(a)のグラフは学習データ数に対する精度の平均値を、(b)のグラフは学習データ数に対する交差エントロピー誤差の平均値を示しています。(a)のグラフからは、NBMFが他の2つの機械学習手法(FCNN、NMF)に比べて、少ない学習データ量において最も高い分類精度を示していることが分かります。また、(b)のグラフからは、NBMFの交差エントロピー誤差は最も低い値を示しており、学習の安定度は高いことが見て取れます。NBMFの3つのソルバー(D-Waveマシン、AE、SA)による値の違いは、この条件下ではほとんど見られませんでした。
https://doi.org/10.1038/s41598-023-43729-z
次に、特徴次元数をパラメータとして変化させた場合の結果を図8に示します。この実験では、学習データ数を150、エポック数を10と設定しました。(a)と(b)のグラフの縦軸は図7と同様で、横軸は特徴次元数を表します。(a)のグラフからは、NBMFが特徴次元数40を超えたあたりから安定した精度を保つことが分かります。一方、FCNNは特徴次元数が増加するにしたがって精度も向上しますが、NMFは逆に特徴次元数の増加とともに精度は低下するという傾向が見られました。また、(b)のグラフからは、NBMFが最も低く安定した交差エントロピー誤差を示していることが分かります。ここでも、NBMFの3つのソルバーによる値の違いはあまり見られませんでした。
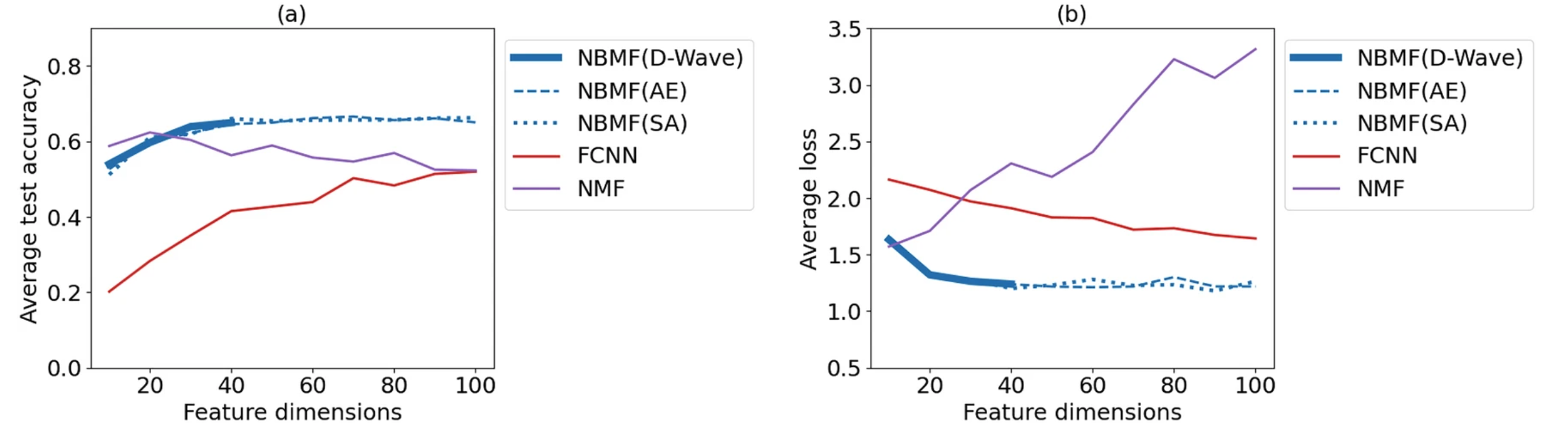
https://doi.org/10.1038/s41598-023-43729-z
続いて、エポック数をパラメータとして変化させた場合の結果を図9に示します。この実験では、学習データ数を300、特徴次元数を40と設定しました。(a)と(b)のグラフの縦軸は図7および図8と同様で、横軸はエポック数を表す片対数グラフです。グラフからは、NBMFはエポック数が10を超えると安定した精度と交差エントロピー誤差を保ち、それ以降も安定していることが分かります。一方で、FCNNはエポック数の増加とともに精度が向上し、交差エントロピー誤差が減少する傾向にあります。特に100エポック以上では結果が安定し、さらに精度と交差エントロピー誤差の点でFCNNがNBMFを上回ることが明らかになりました。
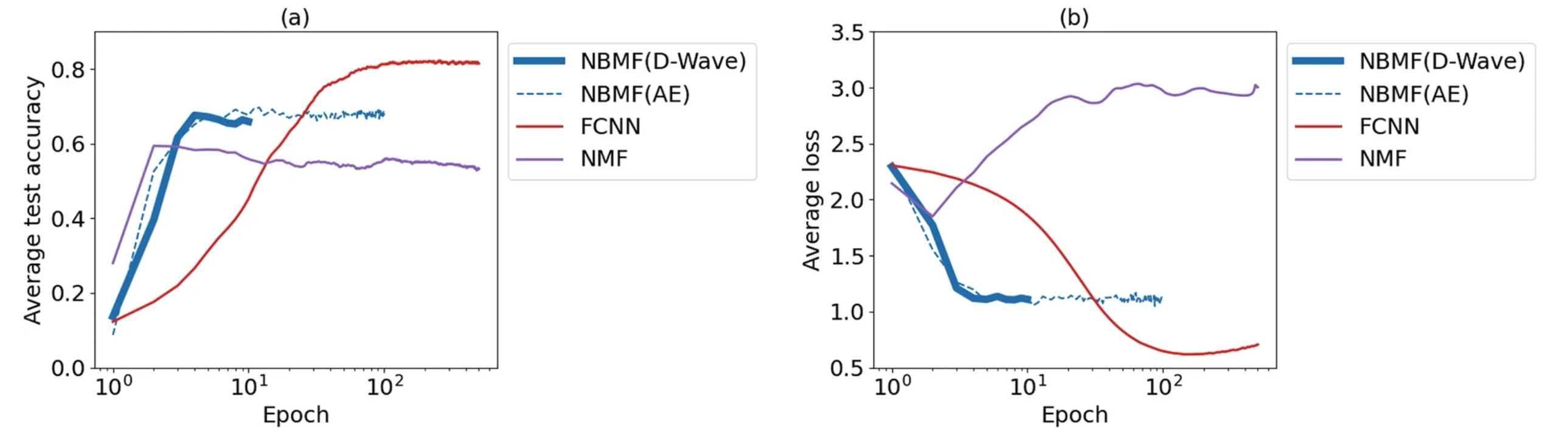
https://doi.org/10.1038/s41598-023-43729-z
3つの結果から共通して言えることは、NBMFは少ないデータ数、少ない特徴次元数、少ないエポック数において、他の機械学習手法を上回る分類性能を示すという点です。また、これら3つの結果から、NMFでは学習データ数、特徴次元数、エポック数の増加とともに、分類精度は横ばいもしくは減少し、交差エントロピー誤差が増加していることが分かりました。このような結果となった原因については、後ほど考察します。
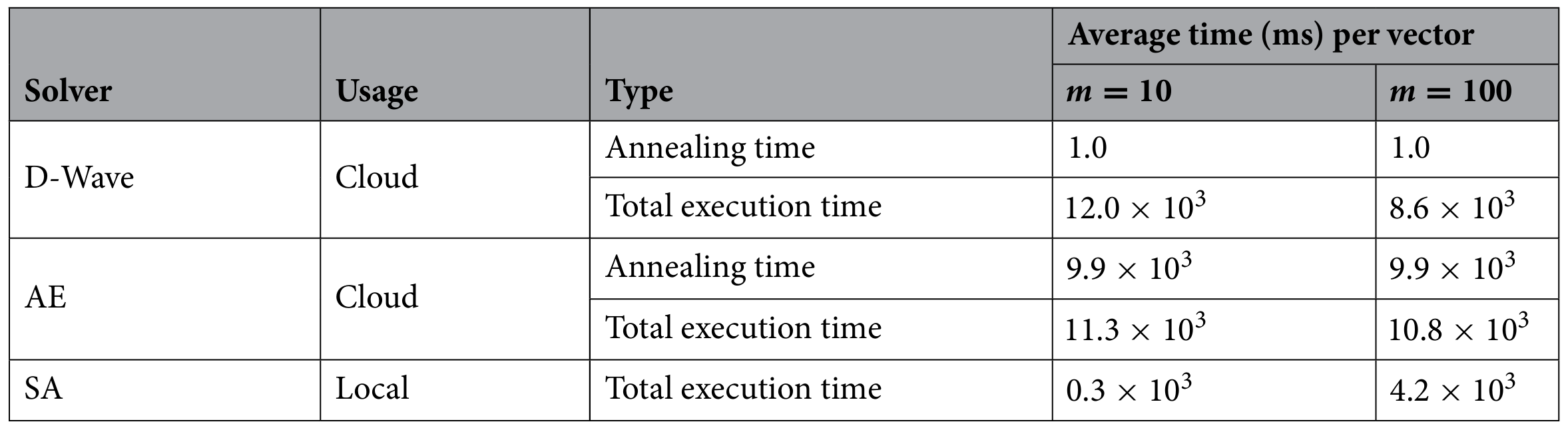
最後に、NBMFの3つのソルバーにおける計算時間を比較しました。D-Waveマシン、AE、SAの3つのソルバーそれぞれでアニーリングにかかった時間をまとめたものが表1です。表から、実行時間が最も短かったのはSAでした。これは、SAがローカルで動作し、通信時間や待機時間が発生しないためです。しかし、アニーリング処理そのものの時間ではD-Waveマシンが最短でした。
https://doi.org/10.1038/s41598-023-43729-z
考察と今後の課題
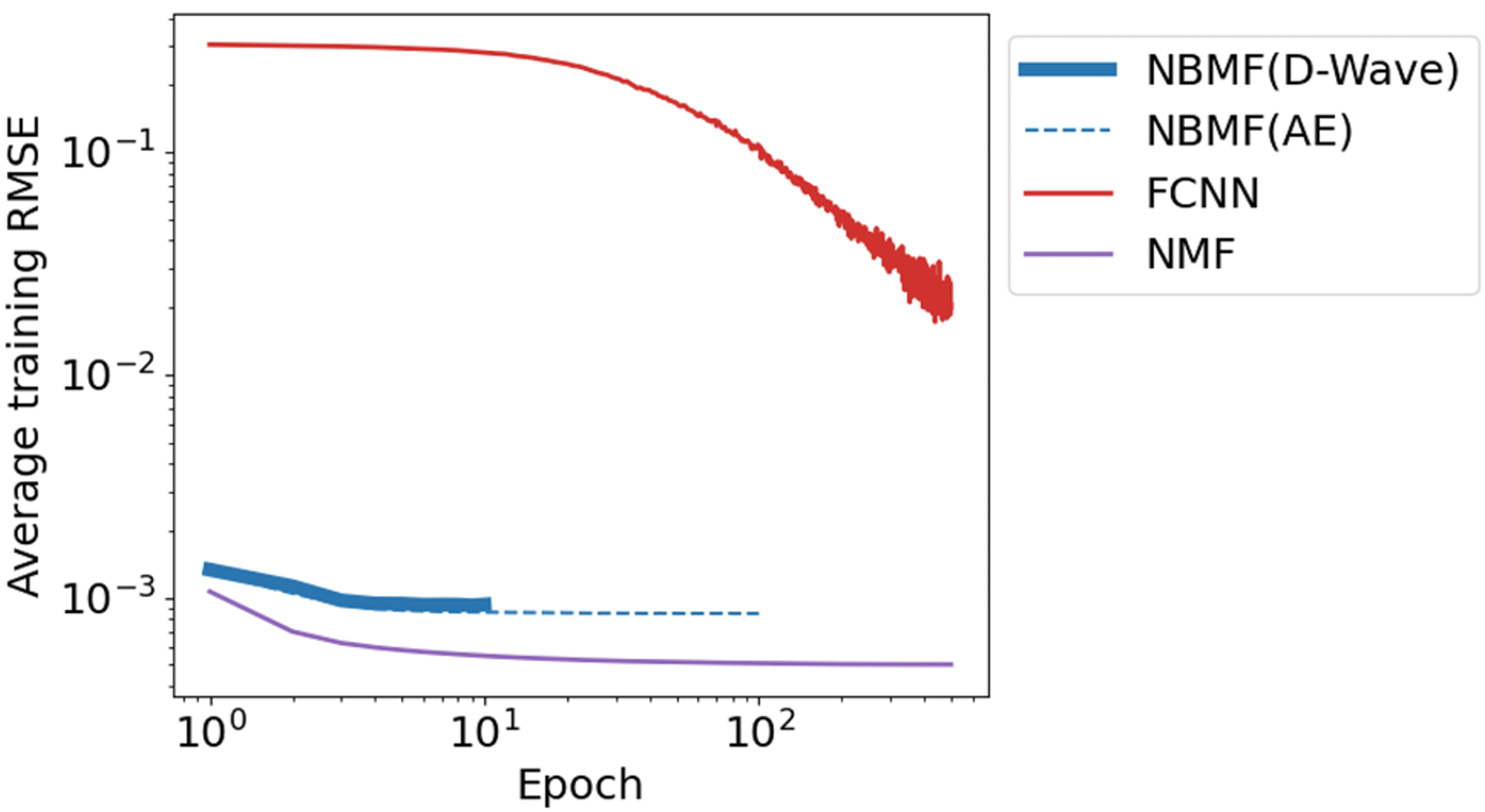
ここでは、非負値行列因子分解(NMF)の分類精度が低かった理由について考察します。実験結果のグラフから、NMFは学習データ数、特徴次元数、エポック数が増加しても精度がほとんど向上しませんでした。さらに、交差エントロピー誤差については、これらのパラメータが増加すると減少するのではなく、むしろ増加する傾向が見られました。これは、NMFが学習データに過剰に適合(過学習)しているため、新しいデータに対する汎化性能が低くなってしまったことを示唆しています。この点について、学習中の二乗平均平方根誤差(RMSE)の点からも考察します。ここでいうRMSEとは、入力行列$V$と$WH$との誤差の二乗の平均値を取り、その平方根を取ったものです。図10に、それぞれの手法におけるエポック数を変化させた場合のRMSEの変化を表すグラフを示しました。
https://doi.org/10.1038/s41598-023-43729-z
グラフから、NMFは3つの手法の中でRMSEの値が最も低いことが分かります。これは、NMFが学習データの再現という点では最も優れていることを意味します。それにも関わらず分類精度が低いのは、NMFがデータの再現に偏りすぎて過学習が生じたためであると考えられます。
今後の主要な課題として、分類モデルの汎用性の向上と量子コンピュータとの通信時間の2点が挙げられます。今回実験に用いたMNISTの数字分類タスクは、古典的な解学習手法ではほぼ100%の精度で達成されており、現在の研究では医用画像診断のような、より難易度の高い実世界の課題に取り組まれています。一方、本論文で提案した分類手法は、MNISTに対しても最大70%程度の精度にとどまっており、実世界への応用には不十分な性能です。これは、NBMFが学習データの再現に重点を置いているため、過学習に陥りやすいことが主な原因であると考えられます。したがって、今後は、より柔軟で複雑な画像の特徴を捉えられるような汎用的モデルへの改良を目指します。また、量子コンピュータとの通信時間も重要な課題です。量子アニーリングマシンを学習に使用する利点は計算時間の短縮ですが、通信時間や待機時間による遅延がボトルネックとなります。実際、本実験でD-Waveマシンがすべてのソルバーの中で結果を返すのに最も時間がかかりました。これはクラウドベースのマシンであることから避けられない問題ですが、通信時間は利用する場所やネットワーク条件によっては短縮できる可能性があります。
結論
本論文では非負二値行列因子分解(NBMF)を多クラス画像分類モデルとして提案しました。そして、MNISTの数字画像分類タスクを用いて、全結合ニューラルネットワーク(FCNN)および非負値行列因子分解(NMF)と分類精度を比較しました。その結果、NBMFは、学習データが少ない場合や短時間での学習が求められる場合といった特定の条件下において、他の手法よりも優れた性能を示すことが明らかになりました。また、NBMFの最適化に用いるアニーリング手法については、通信時間や待機時間という課題は残るものの、アニーリング処理そのものはD-Waveマシンが最速であるという点が判明しました。これらの結果から、特定の状況下においては、量子アニーリングによる機械学習は古典的手法よりも優れているといえます。
参考文献
[1] O’Malley, D., Vesselinov, V. V., Alexandrov, B. S. & Alexandrov, L. B. Nonnegative/binary matrix factorization with a d-wave quantum annealer. PLoS ONE 13, 1–12. https://doi.org/10.1371/journal.pone.0206653 (2018).
[2] 非負値行列分解 “Nonnegative/binary matrix factorization with a D-Wave quantum annealer” by Daniel O’Malley, et al. (2017), /T-Wave/?p=397
[3] Lee, D. D. & Seung, H. S. Algorithms for Non-negative Matrix Factorization. https://dl.acm.org/doi/10.1007/s11704-024-31063-0 (2000).
[4] Wright, S.J. Coordinate descent algorithms. Math. Program. 151, 3–34. https://doi.org/10.1007/s10107-015-0892-3 (2015).
あとがき
本論文では、非負二値行列因子分解(NBMF)を画像分類に応用し、その有効性を既存手法と比較しました。結果として、データ量、特徴数、エポック数が少ないという条件下では、NBMFがニューラルネットワークなどの従来手法を上回る分類精度を示しました。これは、量子アニーリングを活用した機械学習モデルが、限られたリソースや時間内で高いパフォーマンスを発揮できる可能性を示しています。一方で、現状のNBMFでは、MNISTのような比較的単純なタスクであっても最大70%程度の精度にとどまっており、性能面での課題も残されています。今後はNBMFの汎用性を高め、より複雑なデータやタスクへの適用を目指した研究の進展が期待されます。
本記事の作成者
山田竜雅