今回は、量子アニーリングソリューションコンテストに参加した際の発表内容を紹介します。筆者はチームT-QARD-QAPOとして参加し、ポートフォリオ最適化に関するアプリを構想し、発表しました。
はじめに
今回構想したアプリの概要
- ターゲット:個人投資家
- 提供するサービス:
ユーザーが「現実的」かつ「納得」のいくポートフォリオを構築できるように支援する
従来のポートフォリオ最適化の問題点
- 投資比率が細かすぎて資金が少額な個人投資家には再現が困難である
- パフォーマンスだけを最適化の指標にしていて納得の行く投資が困難である
問題点1
銘柄ごとに株価にばらつきがあり、投資比率が細かく設定された最適ポートフォリオを構築するのには、かなりの資金量が必要です。そのため、資金量に限りのある個人投資家が、最適なポートフォリオを再現することは困難です。
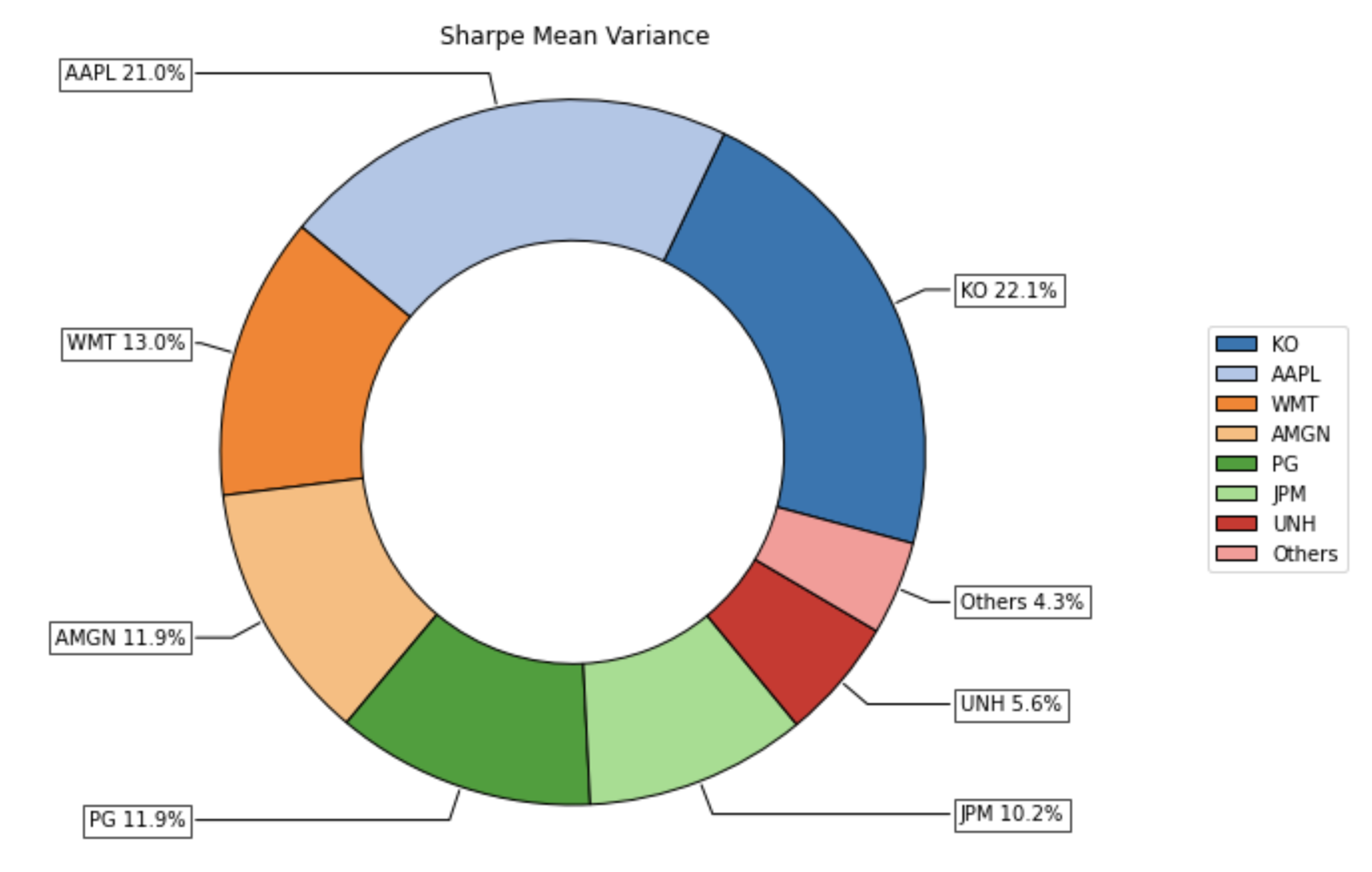
古典的な手法で求めた最適ポートフォリオの例 (Pythonのポートフォリオ最適化ライブラリRiskfolio-Libを使用)
問題点1の解決策
- 投資予算金額を制約条件に含める
- どの銘柄をポートフォリオに組み入れるのかを金額ではなく株数で示す
問題点2
一般的に、ポートフォリオ最適化ではリターンの最大化とリスクの最小化のみに着目して考えています。しかし、各投資家には、各々に「好き・応援したい」や「将来性を信じている」などの理由で選好している分野・銘柄があり、各々の投資したい対象が異なっています。
問題点2の解決策
- 個人の興味や好みを反映できるアルゴリズムを用いる
→量子ポートフォリオ最適化のコスト関数に組み込むのではなく、アルゴリズムとして古典の部分に実装することで変数を増やさず実行可能な形にする。
これは構想にとどまり、まだ実装できていません。
手法
ポートフォリオ最適化とは
ポートフォリオ最適化とは、リスクとリターンを考慮して、最適な資産の組み合わせ(ポートフォリオ)を見つけることです。ポートフォリオ最適化には様々な理論がありますが、今回は現代ポートフォリオ理論に基づいたポートフォリオ最適化を行いました。
現代ポートフォリオ理論とは
現代ポートフォリオ理論(Modern Portfolio Theory)、別名、現代投資理論の説明を以下に示します。
1950年代に米国のハリー・マーコウィツ氏が構築した分散投資理論を基盤とする。資産運用において価格変動リスクを抑えながら一定のリターンを期待するうえでは、ポートフォリオとして多数の銘柄や複数の資産に分散投資するのが有効であり、ポートフォリオ全体の価格変動リスクは、組入銘柄の個々の価格変動リスクおよびその組入比率に加え、任意の2銘柄間の値動きの連動性を表す相関係数で決まることが示された。同氏は投資理論における先駆的な功績により、1990年のノーベル経済学賞を受賞している。
ただ同理論は、銘柄の価格変動リスクは過去から将来にわたって変わらないものとするなど現実にそぐわない仮定を前提にして成り立っている。このため、2008年のリーマン・ショック後には多くの金融資産間の相関係数が高まると同時に、価格変動リスクも増大したため、同理論が提唱するリスクを低減しながらリターンを向上する分散投資効果が期待できなかったとして、理論の限界を示す指摘もある。
引用元:野村證券 証券用語解説集
ポートフォリオ最適化の定式化
リターンの最大化とリスク(共分散)の最小化を最適なポートフォリオの尺度としました。
リターンを表すコスト関数は
[latex]\displaystyle C_{return} = -\sum_{i} w_i x_i \tag{1}[/latex]
-
-
-
- [latex]w_i[/latex] : 各銘柄のリターン
- [latex]x_i[/latex] : バイナリ変数(各銘柄を買うのか買わないのか)
-
-
となります。
また、リスクを最小化するコスト関数は
[latex]\displaystyle C_{risk} = \sum_{i,j} W_{i,j} x_i x_j \tag{2}[/latex]
-
-
-
- [latex]W_{i,j}[/latex] : 各銘柄間の共分散
- [latex]x_i, x_j[/latex] : バイナリ変数(各銘柄を買うのか買わないのか)
-
-
となります。
[latex](1),(2)[/latex]のコスト関数を適当な係数[latex]A[/latex]を付けて足し合わせたものが、今回用いるコスト関数です。
[latex]\displaystyle -A\sum_{i} w_i x_i + \sum_{i,j} W_{i,j} x_i x_j \tag{3}[/latex]
係数[latex]A[/latex]はリターンの最大化とリスクの最小化のどちらに重きを置くのかにより調整する必要があります。
プログラムの実装
この章では、先ほど定式化した問題をPythonを用いて実装します。ここでは、プログラムを紹介するのみにとどめ、実行結果については次章で示します。
株価データの取得
まず、pandas_datareaderを用いて、yahoo financeから株価データを取得します。
今回はアメリカの代表的な株価指数であるDOW30 Indexに採用されている30銘柄の2018年のデータを用いてポートフォリオ最適化を行います。
import pandas_datareader.data as web
import datetime
start = datetime.datetime(2018, 1, 2)
end = datetime.datetime(2018, 12, 31)
DOW30 = ['AAPL','AMGN','AXP','BA','CAT','CRM','CSCO','CVX','DIS','GS','HD','HON', 'IBM','INTC','JNJ','JPM','KO','MCD','MMM','MRK','MSFT','NKE', 'PG','TRV','UNH','V','VZ','WBA','WMT']
stockcodes = DOW30+DOW30
data = web.DataReader(DOW30, 'yahoo', start, end)
df_price_DOW30 = data['Adj Close']
データの加工
先程取得した株価データから、各銘柄の一日当たりの幾何平均リターンと共分散行列を求めます。
※補足(幾何平均とは)
一般的に用いられる平均を算術平均(arithmetic mean)といい、算術平均[latex]\bar{X}[/latex]は、
[latex]\bar{X}=\dfrac{X_1+X_2+X_3+ \cdots +X_n}{n}[/latex]
で表されます。一方で、幾何平均(geometric mean)とは、対象とする集合のデータを掛け合わせて基準となる値が算出され、幾何平均[latex]X_G[/latex]は、
[latex]X_G=\sqrt[n]{X_1 \times X_2 \times X_3 \times \cdots \times X_n}[/latex]
で表されます。計算方法から相乗平均と呼ばれることもあり、主に増減率や成長率などの平均を求めるのに使用されます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats.mstats import gmean
df_price0 = pd.merge(df_price, df_price, on='Date')
rates = []
for sc in stockcodes:
df = df_price.loc[:,sc]
return_rate = np.zeros(len(df.values))
for k in range(len(df.values)-1):
return_rate[k+1] = (df[k+1] - df[k])/df[k]
rates.append(return_rate)
N = len(stockcodes)
list_price_start = np.zeros(N)
for n in range(N):
list_price_start[n] = df_price.loc['2018-01-02',stockcodes][n]
list_price_end = np.zeros(N)
for n in range(N):
list_price_end[n] = df_price.loc['2018-12-31',stockcodes][n]
#幾何平均w_1を求める
for k in range(N):
for n in range(len(rates[1])):
rates[k][n] = rates[k][n]+1
w_1 = np.zeros(N)
for k in range(N):
w_1[k] = gmean(rates[k])
w = np.zeros(N)
for n in range(N):
w[n] = w_1[n]-1
for k in range(N):
for n in range(len(rates[1])):
rates[k][n] = rates[k][n]-1
コスト関数を準備する
先程求めた各銘柄の一日当たりの幾何平均リターンと共分散行列をもとに、PyQUBOを使って最適化のためのコスト関数を準備します。
from pyqubo import Array, Constraint, Placeholder, solve_qubo
x = Array.create('x', shape=N, vartype='BINARY')# BINARY変数
K = 1000 #投資額
constr = (((np.dot(x,list_price_start))-0.9*K)/10)**2 #予算制約
#リターンに関するコスト
cost = 0
for i in range(N):
cost = cost - w[i]*x[i]
#リスクに関するコスト
cost2 = 0
for i in range(N):
for j in range(N):
cost2 = cost2 +x[i]*x[j]*np.sum((rates[i]-w[i])*(rates[j]-w[j]))/len(rates[i])
#コスト関数
cost_func = 2*cost + cost2 + Placeholder('a')*Constraint(constr, label='Kconstr')
model = cost_func.compile()
max_coeff = np.max(abs(w))
#制約の強さを調整する
feed_dict = {'a': 17.0*max_coeff}
qubo, offset = model.to_qubo(feed_dict=feed_dict)
最適化を実行する
今回は、SQA(Simulated Quantum Annealing)ライブラリーであるOpenJijを利用して最適化を実行します。
from openjij import SQASampler
sampler = SQASampler(num_sweeps=3000)
R = 300
sampleset = sampler.sample_qubo(qubo,num_reads=R)
print(sampleset.record)
各銘柄の出現頻度
量子アニーリングによって導かれるポートフォリオは一通りではありません。そのため、何かしら工夫をしてポートフォリを1つに確定したいと考えました。そこで、各銘柄の出現頻度を偏差値で評価し、出現頻度の高い銘柄でポートフォリオを構築することにしました。ただし、今回実装したプログラムでは偏差値で評価する意味がありません。単に、出現回数をカウントするだけで十分です。ただ、今後の展開のためにここでは偏差値で評価しています。
仮定
ここで行っている銘柄選別は以下の仮定によるものです。
「量子アニーリングによって求めた解の中には、良い銘柄ほど多く含まれる」
例:A,B,C,D,Eの5銘柄から2銘柄選ぶ最適化を5回行ったときの結果が以下のようだったとします。ここで、0は銘柄が選ばれなかったことを意味し、1は選ばれたことを意味します。
| 銘柄 | 結果1 | 結果2 | 結果3 | 結果4 | 結果5 |
|---|---|---|---|---|---|
| a | 0 | 1 | 0 | 0 | 1 |
| b | 1 | 1 | 1 | 1 | 0 |
| c | 0 | 0 | 0 | 1 | 0 |
| d | 0 | 0 | 0 | 0 | 0 |
| e | 1 | 0 | 1 | 0 | 1 |
このとき、銘柄Dは一度も選ばれていないのでポートフォリオにとって悪い銘柄だと判断し、5回中4回選ばれている銘柄Bはポートフォリオにとって良い銘柄だと判断します。
出現頻度を求める
record_avg = np.mean(record_count)
record_std = np.std(record_count)
DV = np.zeros(N)
for n in range(N):
DV[n] = (record_count[n] - record_avg)/record_std*10 + 50
DV
実行結果を確認する
先程の最適化の結果をもとにポートフォリオを構築します。ここでは、最もエネルギーが低い状態となったポートフォリオ(list_min)と最も出現頻度が高い銘柄で構成したポートフォリオ(list_DV)の2通りのポートフォリオを構築し、そのリターンとリスクを比較・評価します。
#list_minを求める
x_min = min(sampleset.record.energy)
for n in range(R):
if sampleset.record.energy[n] == x_min:
list_min = sampleset.record.sample[n]
list_min_tiker = []
for n in range(N):
if list_min[n] == 1:
list_min_tiker.append(stockcodes[n])
#list_DV を求める
DV_best = sorted(DV, reverse=True)[:15]
list_DV = np.zeros(N)
list_DV_tiker = []
for k in range(N):
if np.dot(list_DV,list_price_start)< K-200:
for n in range(N):
if DV[n] == DV_best[k]:
list_DV[n] = 1
list_DV_tiker.append(stockcodes[n])
print(list_min_tiker)
print(list_DV_tiker)
実行結果を評価する
求めたポートフォリオのリターンとリスク及び初期投資額を表示させます。
#最低コストに基づくポートフォリオ
cost2_return = 0
for i in range(N):
for j in range(N):
cost2_return = cost2_return +list_min[i]*list_min[j]*np.sum((rates[i]-w[i])*(rates[j]-w[j]))/len(rates[i])
total_return = np.dot(list_price_end,list_opt)/np.dot(list_price_start,list_opt)
ratio = total_return/(cost2_return)
assets = np.dot(list_price_start,list_min)
print('Return(%):')
print((total_return-1)*100)
print('Risk:')
print((cost2_return))
print("Ratio:")
print(ratio)
print('Total Assets:')
print(assets)
#出現頻度に基づくポートフォリオ
cost2_return = 0
for i in range(N):
for j in range(N):
cost2_return = cost2_return +list_DV[i]*list_DV[j]*np.sum((rates[i]-w[i])*(rates[j]-w[j]))/len(rates[i])
total_return = np.dot(list_price_end,list_DV)/np.dot(list_price_start,list_DV)
ratio = total_return/(cost2_return)
assets = np.dot(list_price_start,list_DV)
print('Return(%):')
print((total_return-1)*100)
print('Risk:')
print((cost2_return))
print("Ratio:")
print(ratio)
print('Total Assets:')
print(assets)
資産推移の可視化
求めたポートフォリオの資産推移を可視化して、どのような価格変動をしているのかを確かめます。
最もエネルギーが低い状態となったポートフォリオの資産推移を”min_energy”と表し、最も出現頻度が高い銘柄で構成したポートフォリオの資産推移を”appearance_ratio”と表します。
w_assets = pd.DataFrame(np.vstack([list_min, list_DV]).T, index=df_price1.columns, columns=['min_energy', 'appearance_ratio'])
#資産の推移
pf_value = df_price1.dot(w_assets)
#期初の値で規格化
pf_value.min_energy = pf_value.min_energy / pf_value.min_energy[0]
pf_value.appearance_ratio = pf_value.appearance_ratio / pf_value.appearance_ratio[0]
#資産推移をグラフで表示する
pf_value.plot(figsize=(9, 6))
結果・バックテスト
今回、ポートフォリオ最適化によって求めた2種類のポートフォリオが、最適化の対象銘柄のもととなる指数(DOW30 Index)を上回ることができたのかを検証しました。以下には、2020年(上昇相場)と2018年(下落相場)のデータに基づくポートフォリオ最適化の実行結果とそのポートフォリオのバックテストの結果を示しています。実験は2回行い、実行結果①、実行結果②として結果を示しています。
※補足(バックテストとは)
バックテストとは、ポートフォリオの有効性(ポートフォリオを求める手法の有効性)を検証するために、過去の実際のデータをポートフォリオに適用して、その結果(リターン・リスクなど)を確かめることです。このとき、様々な時間軸でバックテストを行うことで、より精度の高い検証が行えます。
2020年のデータに基づく実行結果
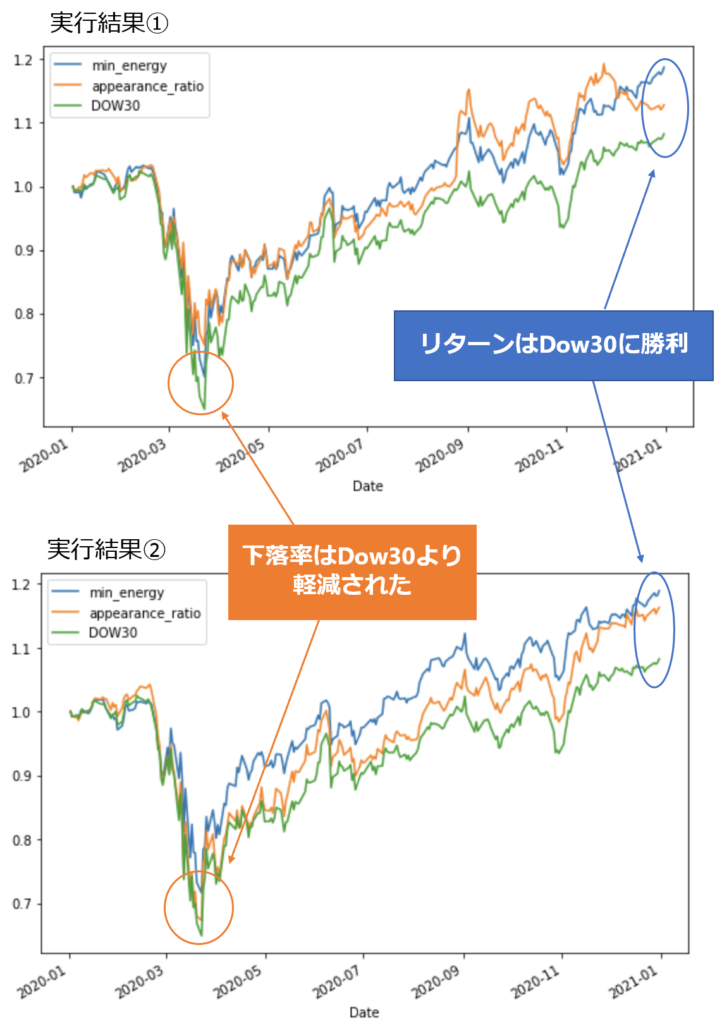
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
| 実行結果① | 実行結果② | |||
|---|---|---|---|---|
| 最低コスト | 出現頻度 | 最低コスト | 出現頻度 | |
| リターン | 18.75 | 12.82 | 18.91 | 16.29 |
| リスク | 0.03107 | 0.01861 | 0.04001 | 0.03042 |
| 初期投資額 | 902.9 | 810.7 | 1439.0 | 865.4 |
2020年のデータに基づくポートフォリオのバックテスト
2021年のデータを適用した結果
実行結果①
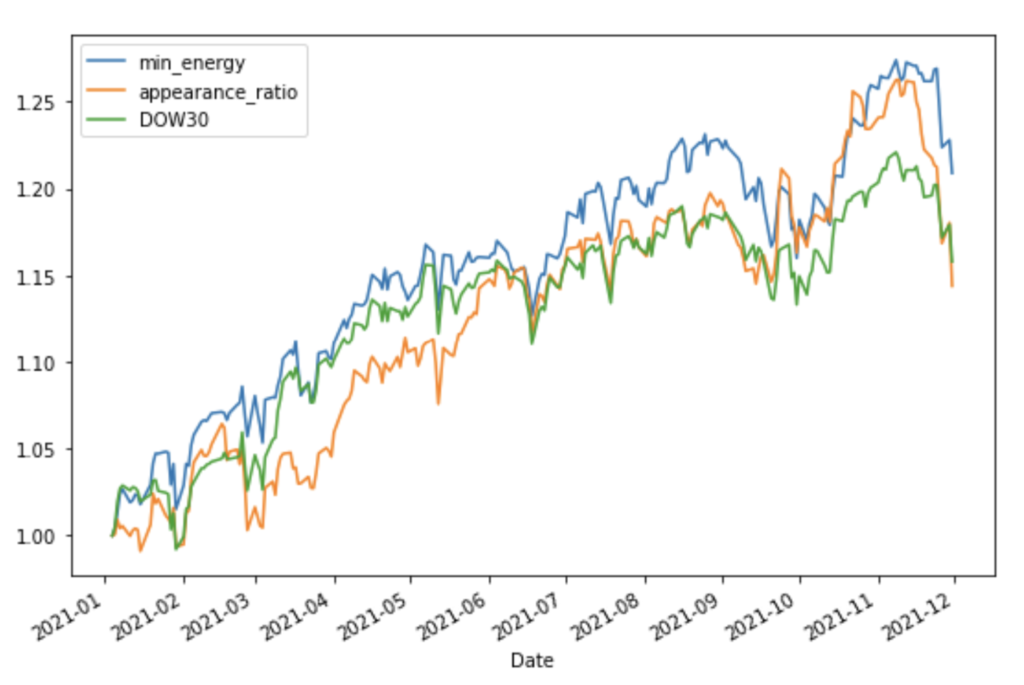
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
実行結果②
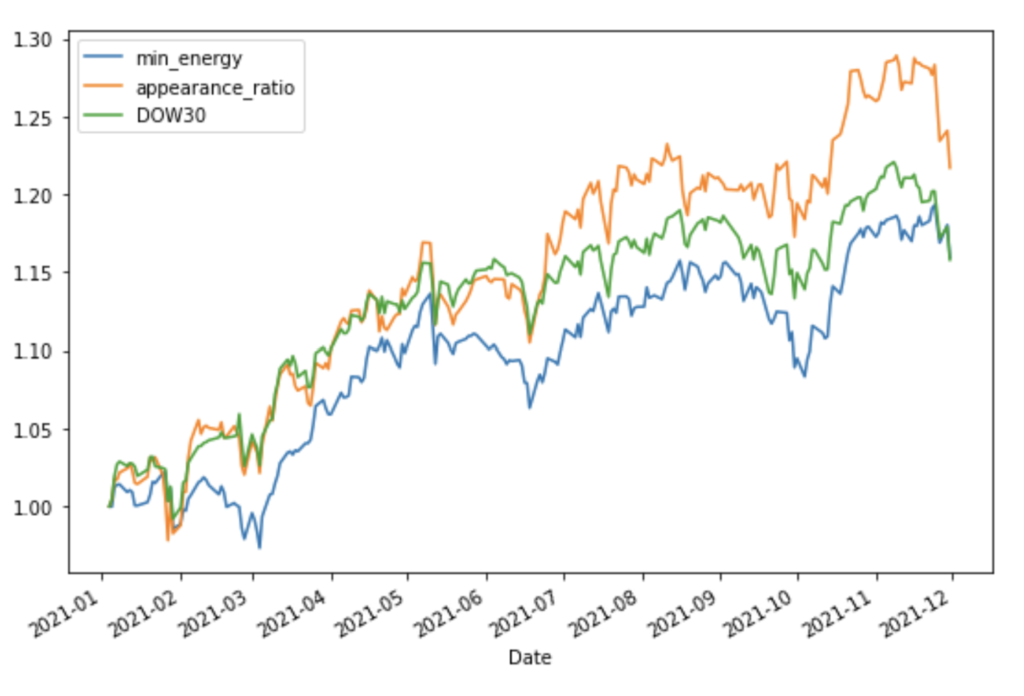
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
- 2021年のデータに適用した場合、Dow30 Index と同等もしくは、やや良い結果となりました。
- 最低コストに基づくと出現頻度に基づくポートフォリオとでは、実行毎に優劣が入れ替わり評価できませんでした。
2018年のデータに基づく実行結果
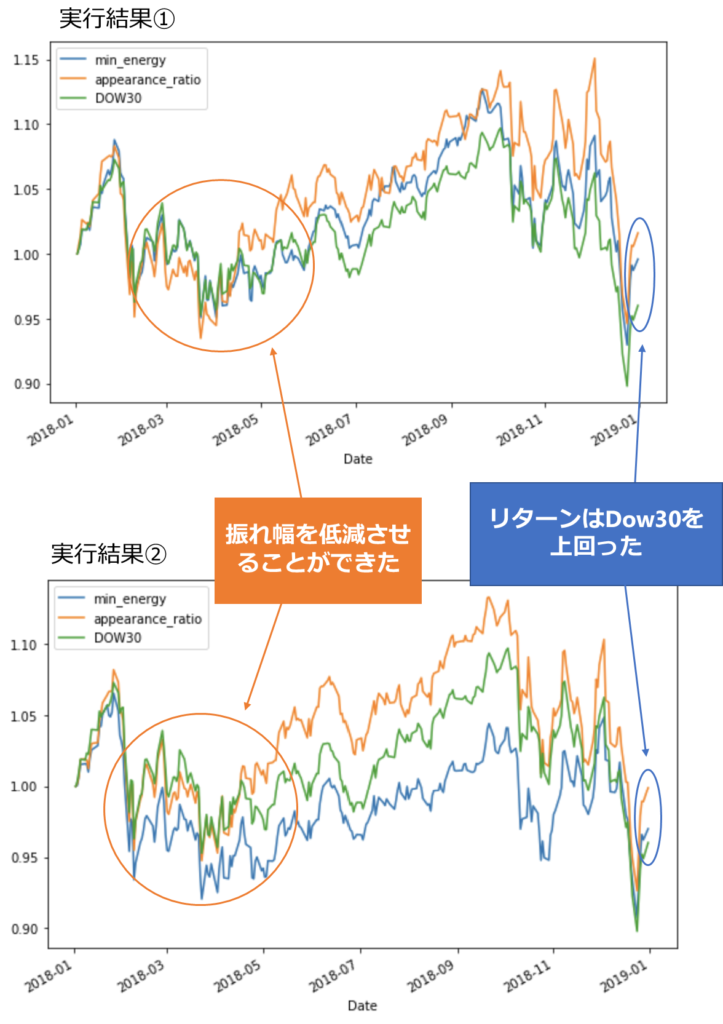
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
| 実行結果① | 実行結果② | |||
|---|---|---|---|---|
| 最低コスト | 出現頻度 | 最低コスト | 出現頻度 | |
| リターン | -0.414 | 1.60 | -3.01 | -0.10 |
| リスク | 0.01977 | 0.00731 | 0.01459 | 0.01380 |
| 初期投資額 | 1172.6 | 890.8 | 1203.2 | 893.6 |
2018年のデータに基づくポートフォリオのバックテスト
2019年のデータを適用した結果
実行結果①
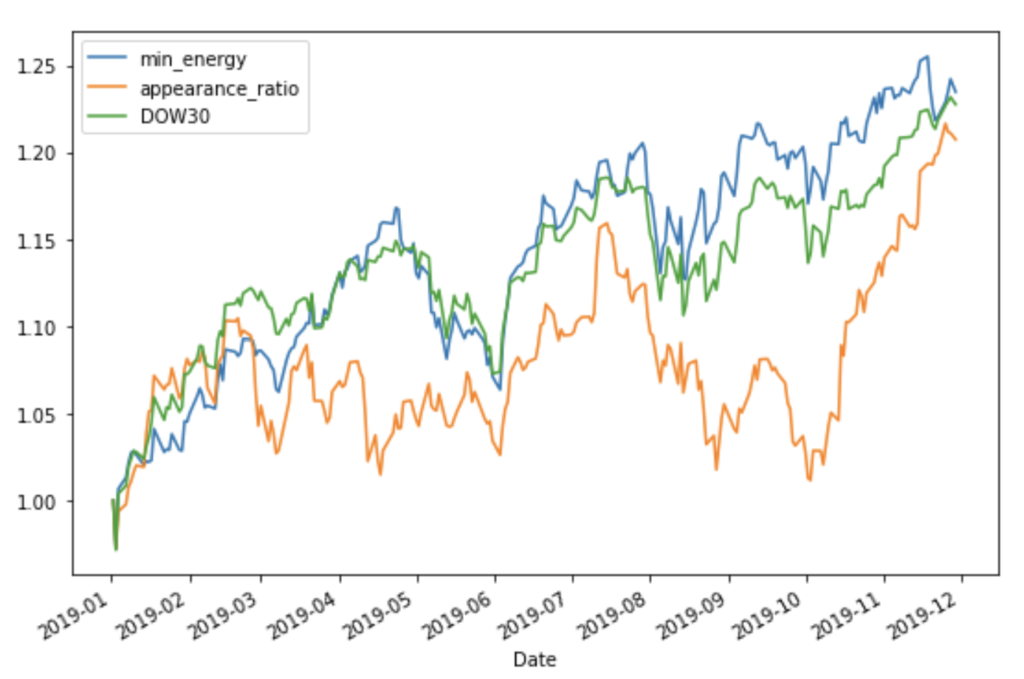
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
実行結果②
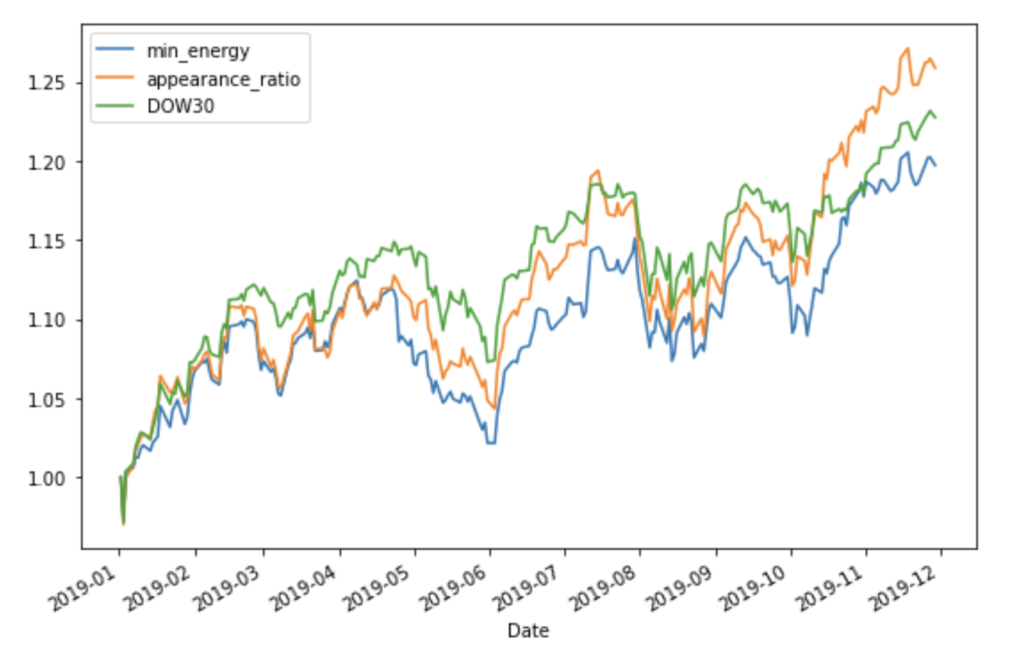
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
- Dow30 Index と同等もしくは、やや良い結果となりました。
- 最低コストに基づくポートフォリオと出現頻度に基づくポートフォリオとでは実行毎に優劣が入れ替わり、優劣を評価できませんでした。
2020年のデータを適用した結果
実行結果①

資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
実行結果②
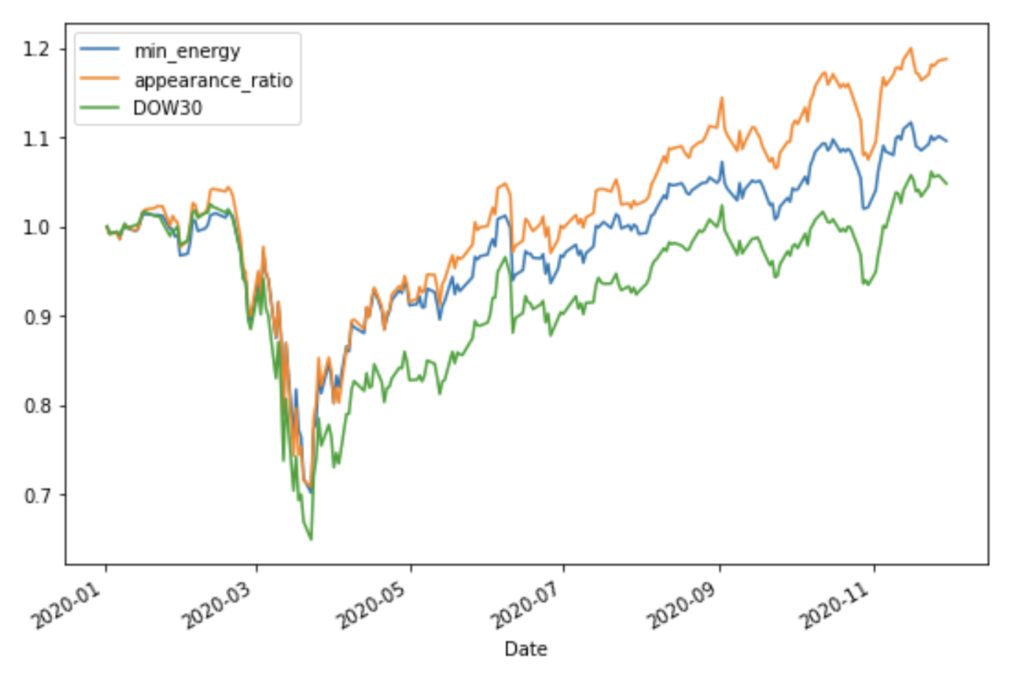
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
- Dow30 Index よりも、かなり良い結果となりました。
- 最低コストに基づくよりも、出現頻度に基づくが優位な傾向にあります。
- 出現頻度に基づくは実行毎の結果が安定していました。
2021年のデータを適用した結果
実行結果①
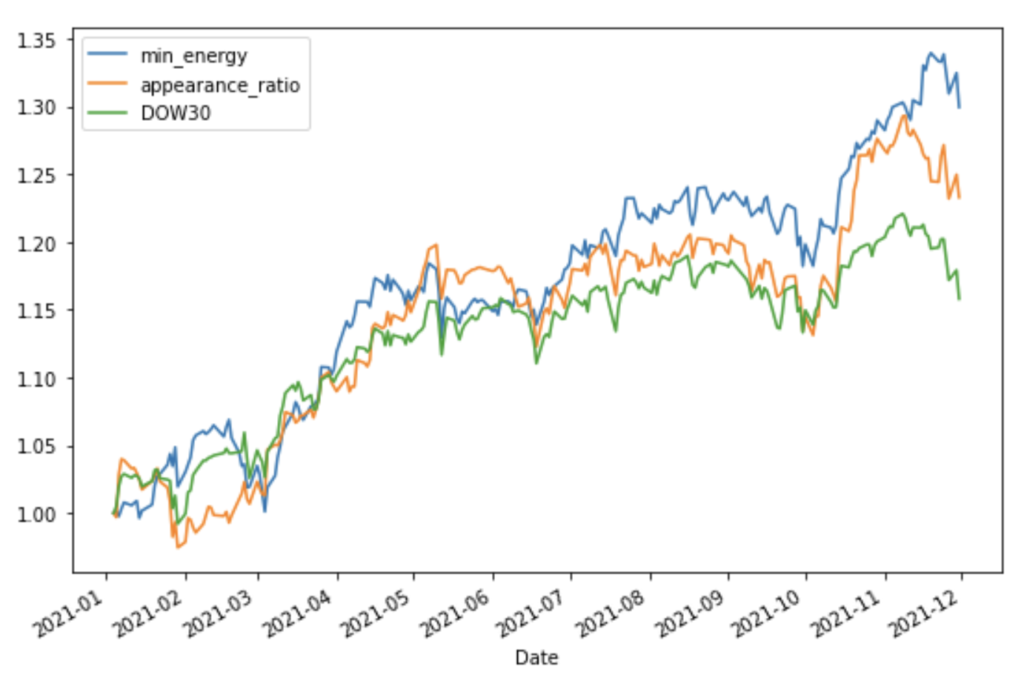
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
実行結果②
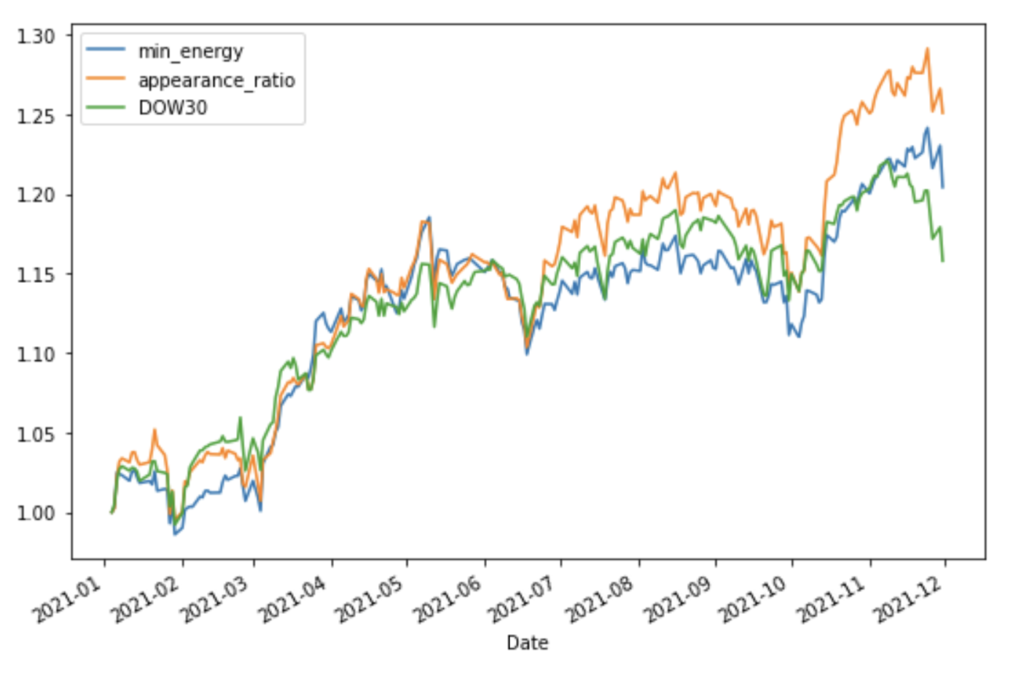
資産推移のグラフ(縦軸は初期値1で規格化された資産価格を表します)
- Dow30 Index よりも、かなり良い結果となりました。
- 最低コストに基づくポートフォリオと出現頻度に基づくポートフォリオとでは実行毎に優劣が入れ替わり評価できませんでした。
まとめ
- コストが最小になるポートフォリオは、結果が安定しませんでしたが、出現頻度で評価したポートフォリオは安定してDow30Indexを上回りました。
- 別の年のデータに適用した場合でも、出現頻度で評価したポートフォリオは、Dow30Indexと同等もしくは、上回りました。
- 別の年のデータに適用した場合において、大きくDow30Indexに負けることはほとんどありませんでした。
今後の課題
- 各銘柄間の共分散をリスクの尺度にしているため、同一銘柄が複数回選ばれることがありませんでした。ですので、銘柄ごとに株価が異なることを考慮して、同一銘柄が複数回選ばれるようにリスクを設定したいです。
- 個人の選好を反映させるアルゴリズムを実装できていませんので、今後実装したいです。
最後に
参考文献・サイト
本記事の担当者
長手晟也
[mathjax]