文献情報

タイトル: Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models
著者: Marcello
Benedetti, John Realpe-Gómez, Rupak Biswas and Alejandro Perdomo-Ortiz
書誌情報: Phys. Rev. X
7, 041052 (2017)
DOI : 10.1103/PhysRevX.7.041052

概要

ボルツマン機械学習では対数尤度関数を最大化するために、ギブス・ボルツマン分布からのサンプリングによる平均値を計算する必要があります。その方法の一つとして、マルコフ連鎖モンテカルロ法 (MCMC)が使われています。しかし、MCMCは初期状態から平衡状態への緩和に長時間の計算を要する場合があります。また、緩和した後も平均値を精度良く求めるための十分なサンプリング数の確保に時間がかかるといった課題もあります^[1]。そこで本論文では、D-Waveマシンから得られる出力の分布がギブス・ボルツマン分布に近いことを利用して、平均値の計算にD-Waveマシンを用います。本手法により、手書き数字画像の生成・復元が可能であることに加え、ランダムなイジング模型も学習可能であることを示します。

背景・課題

ボルツマン機械学習とは

$ N $次元のベクトルで表される$ D組 $のデータ$ \sigma^{(d)} $が、経験分布に従って出力されているとします。D-Waveマシンから得られる解候補の分布はギブス・ボルツマン分布に近いことが知られているので、ギブス・ボルツマン分布がデータの経験分布に近づくようにパラメータを調整します。

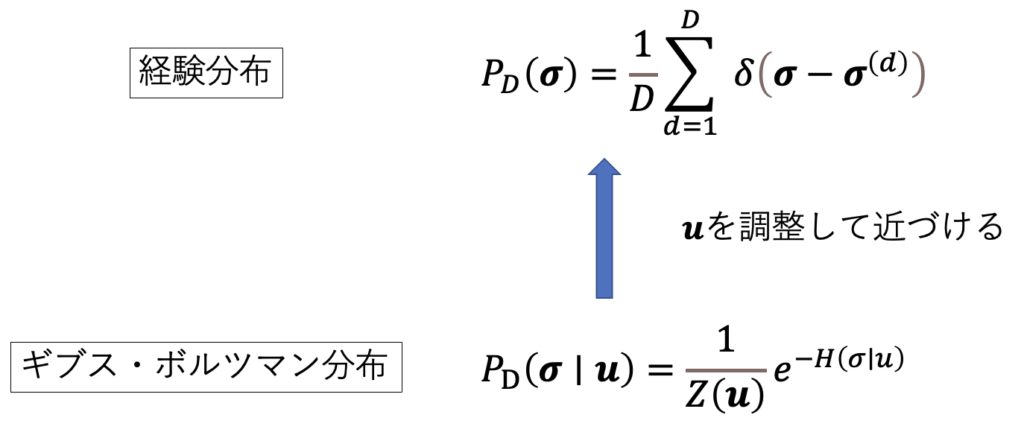
続いて、学習方法について説明します。パラメータを更新する際、ギブス・ボルツマン分布がどれくらい経験分布に近づいたのかを知る必要があります。そこで、２つの確率分布の類似度を表す尺度として、カルバック・ライブラー (KL)情報量が用いられます。確率分布$ P(\sigma), Q(\sigma) $とすると、KL情報量は次のように表されます。

\begin{equation}
D_{K L}(P \mid Q)=\sum_{\sigma} P(\boldsymbol{\sigma}) \log
\left(\frac{P(\boldsymbol{\sigma})}{Q(\boldsymbol{\sigma})}\right)
\end{equation}

KL情報量$ D_{K L}(P \mid Q) $ は常に負でない値を持ち、 $ P = Q $ の場合のみ $D_{K L}(P \mid Q) = 0$となります。 2つの確率分布が差異が大きい場合は、KL情報量は大きい値をとります。ここで、$ P(\sigma) $に経験分布、$Q(\sigma)$にボルツマン分布を代入すると、次のようになります。

\begin{equation}
D_{K L}\left(P_{D}(\boldsymbol{\sigma}) \mid P(\boldsymbol{\sigma} \mid
\boldsymbol{u})\right)=\sum_{\sigma} P_{D}(\boldsymbol{\sigma}) \log P_{D}(\boldsymbol{\sigma})-\sum_{\sigma}
P_{D}(\boldsymbol{\sigma}) \log P(\boldsymbol{\sigma} \mid \boldsymbol{u})
\end{equation}

パラメータに関する部分は第２項のみなので、$ D_{KL} $を最小化するには、第２項を最大化すればよいということになります。第２項を$ L(u) $とし、$P_{D}(\sigma)$に経験分布を代入すると、

\begin{equation}
L(\boldsymbol{u})=\frac{1}{D} \sum_{d=1}^{D} \log
P\left(\boldsymbol{\sigma}=\boldsymbol{\sigma}^{(d)} \mid \boldsymbol{u}\right)
\end{equation}

となります。この$ L(u) $を対数尤度関数といいます。$ L(u) $を最大化するために用いる手法が勾配法です。

\begin{equation}
\boldsymbol{u}[t+1]=\boldsymbol{u}[t]+\eta \frac{\partial L(\boldsymbol{u})}{\partial
\boldsymbol{u}}
\end{equation}

この式を用いてパラメータを更新していきます。対数尤度関数$ L(u) $の偏微分は次式で求められます。

\begin{equation}
\frac{\partial L(\boldsymbol{u})}{\partial \boldsymbol{u}}=-\frac{1}{D} \sum_{d=1}^{D}
\frac{\partial H \left(\boldsymbol{\sigma}=\boldsymbol{\sigma}^{(d)} \mid \boldsymbol{u}\right)}{\partial
\boldsymbol{u}}+\left\langle\frac{\partial H(\boldsymbol{\sigma} \mid \boldsymbol{u})}{\partial
\boldsymbol{u}}\right\rangle_{\boldsymbol{u}}
\end{equation}

ここで、第2項はギブス･ボルツマン分布からのサンプリングによる平均値⟨･･･⟩_𝒖を持つので一般には計算が難しく、MCMCなどの手法が用いられます。しかし、上述したようにMCMCはサンプリングに時間がかかってしまいます。そこで、D-Waveマシンを用いてサンプリングを行い、平均値を計算します。

方法

画像の生成・復元

図2(a)
はボルツマン機械学習の全体像です。パラメータをD-Waveマシンに入力すると、ギブス・ボルツマン分布に従う出力が得られます。これと画像データを比較して勾配法を行い、パラメータを更新していきます。具体的には次のように学習を行います。本論文では、2つの確率分布の類似度を表すために、KL情報量ではなく量子相対エントロピー$S$を用います。$S$の値が小さいほど、2つの確率分布は似ていることを表します。

\begin{equation}
S\left(\rho_{\mathcal{D}} \| \rho\right)=Tr \rho_{\mathcal{D}} \ln \rho_{\mathcal{D}}-Tr
\rho_{\mathcal{D}} \ln \rho
\end{equation}

ただし、$ \rho_{D} $ はデータの経験分布を表す密度行列、$ \rho $ はギブス・ボルツマン分布を表す密度行列である。

$ S $を最小化するために、次の勾配法を用いてパラメータを更新し、これを繰り返します。

\begin{equation}
\begin{aligned}
&J_{i j}^{(k l)}(t+1)=J_{i j}^{(k l)}(t)+\eta \frac{\partial
S}{\partial J_{i j}^{(k l)}} \\
&h_{i}^{(k)}(t+1)=h_{i}^{(k)}(t)+\eta \frac{\partial S}{\partial
h_{i}^{(k)}}
\end{aligned}
\end{equation}

ここで、$ k, l $ は各データのインデックスを示しています。以上が、画像データを学習する方法です。

続いて、画像データに欠損箇所がある場合の復元方法について説明します。全体像は 図2 (b) のようになります。まず、欠損した部分以外を局所磁場で固定します。それと同時に、図2 (a) で学習済みのパラメータ (相互作用)
をD-Waveマシンに入力します。例えば、欠損した「2」の画像は次のようになります (図3)。

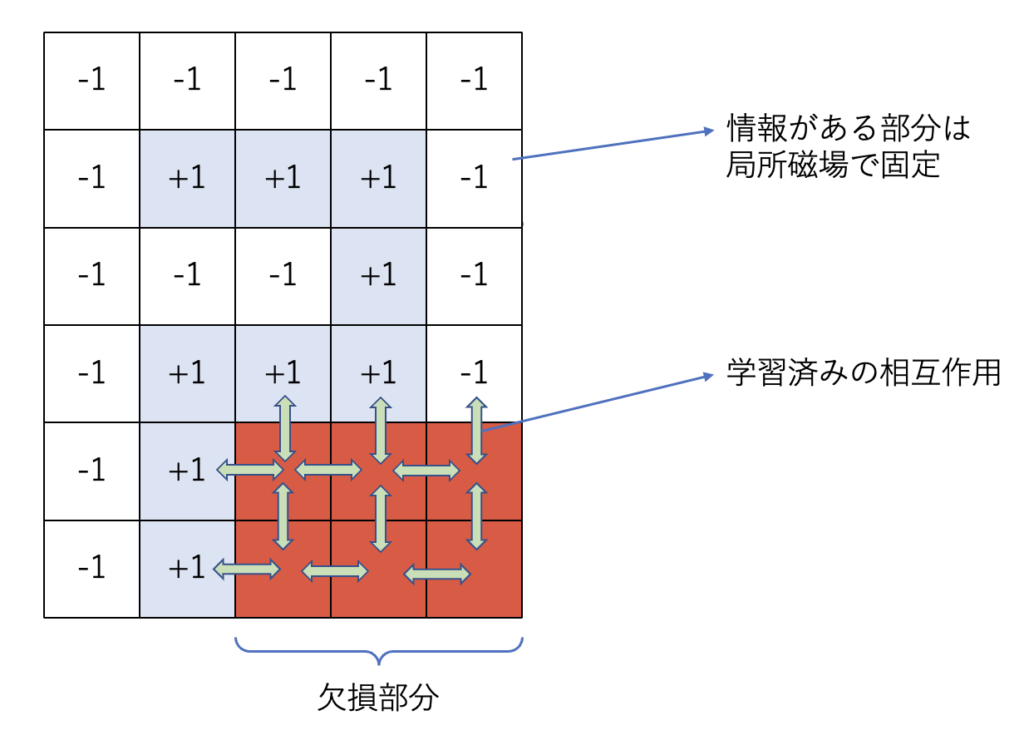
既知のデータおよび学習済みの相互作用によって、欠損箇所のスピン値 ($ \pm 1 $) が決定し、復元することができます。

実験・結果

本論文では、3種類のデータセットで実験を行いました。

(1) 手書き数字の学習 – OptDigits

まず、手書き数字の小さい画像を学習できるか検証します。使用可能な変数に制限があるため、画像のトリミングを行なっています。また、しきい値を4として$ \pm 1 $ の2変数に変換をしています (図4)。

続いて、提案手法を用いて学習を行います。それに加え、学習性能を検証するために画像の復元を行います。結果は次のようになります。

図5 (a) はテストセットの画像です。この画像に対して、ランダムに50%の情報を欠損させたのが(b)です。1回学習すると図5 (c)
のように数字とは認識し難い画像が復元されていることが分かります。ここから学習回数を増やしていくと、(d)-(f)のように復元されます。(a)と(f)を比較すると、おおよそ復元できていることが確認できます。また、これ以上学習を繰り返すと、D-Waveマシンのダイナミックレンジを超えてしまうパラメータがあるため、6000回で学習を停止しています。

今回用いた手書き数字のデータには欠損箇所によっては、復元先が一意的に定まらない場合があります。

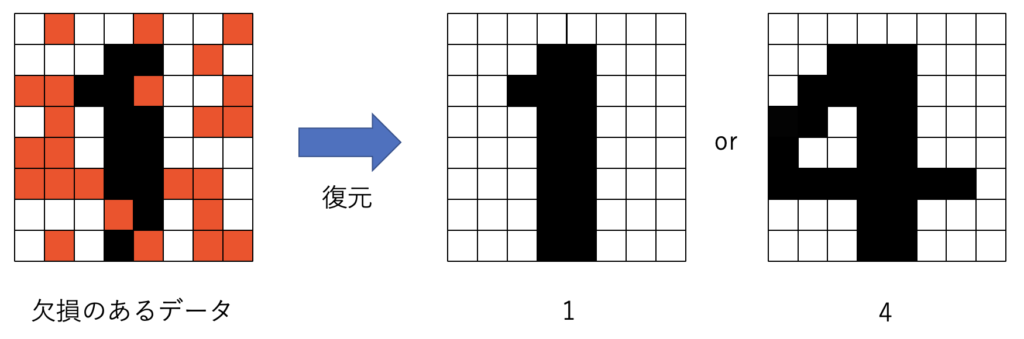
そこで、次の検証では復元が成功しているのかを明確にするために、復元先が一意的に定まるようなデータを用いていきます。

(2) 正解が明確なデータの学習 – BAS

BASデータセットは、$ 7 \times 6 $ の画像で構成され、それぞれの行(列)に黒(-1)または白(+1)がランダムに塗られています。

結果の見方は、OptDigitsの場合と同様です。BASデータセットでも学習回数を増やすことにより、高い精度で復元出来ていることが確認できました。最後に、ランダムなイジング模型でも正しく学習出来るのか検証します。

(3) SK模型の学習

SK模型とは、すべてのスピン間に対して同じ確率分布に従った相互作用を与えるイジング模型です。本論文では、$ N=15 $, $ h_{i}=0 $, 逆温度 $\beta=1$, 平均 $ \mu=0 $, 標準偏差 $ \sigma=2/\sqrt{N} $として、$D=150$のトレーニングセットを作成しました。ここでは学習方法として、厳密勾配を用いる方法、シミュレーテッド・アニーリング (SA) 、量子アニーリング (QA)
の３つの方法を用います。QAに関しては、画像の復元と同様にD-Waveマシンを用いて学習を行います。また、学習速度を比較するための尺度として、次の平均対数尤度を用います。

\begin{equation}
\begin{aligned}
\Lambda_{\mathrm{av}}(\delta) &= \frac{1}{L} \sum_{\ell=1}^{L} \log
Q\left(\mathbf{s}^{(\ell)}\right) \\
&= -\beta \frac{1}{L} \sum_{\ell=1}^{L}
E\left(\mathbf{s}^{(\ell)}\right)-\log Z(\beta)
\end{aligned}
\end{equation}

以下に結果を示します。

緑の帯がトレーニングセットの値なので、これに一致すれば学習が成功したと言えます。学習率が同じ場合 (図8 (a)) では、厳密勾配を用いた方がSAよりも速く学習出来ていることが分かりました。一方、学習率を変えた場合(図8 (b))
では、厳密勾配よりもQAの方が速く学習できていることが分かりました。

結論

今回はMCMC の代わりに D-Wave マシンを用いてサンプリングを行うボルツマン機械学習の手法を提案しました。実験の結果、提案手法により手書き数字やランダムなイジング模型を学習できることが確認できました。また、SK模型については厳密勾配やSAよりもD-Waveマシンを使った方が速く学習できることが分かりました。

編集者あとがき

本論文を解説することで、QAとボルツマン機械学習の両方を勉強することが出来ました。最適化のために作られたD-Waveマシンが最適でない解を返してしまうという短所が、機械学習の分野で活きるというストーリーがとても面白かったです。論文に関しては、MCMCといった従来のサンプリング手法と比べ、どれくらいD-Waveマシンを用いた手法が優れているのか示されていれば良かったです。

参考文献

[1]量子アニーリングの基礎, 西森秀稔, 大関真之, 2018

本記事の担当者

鹿内怜央 (メンタリング: 丸山尚貴、羽場廉一郎)