文献情報

• タイトル：On neural network kernels and the storage capacity problem
• 著者：Jacob A. Zavatone-Veth, Cengiz Pehlevan
• 書誌情報：https://doi.org/10.1162/neco_a_01494

概要

本記事で紹介する論文は，ニューラルネットワーク（NN）の性能と活性化関数の関係にまつわる2つの研究の流れの間の関連性を指摘するものです．

1つ目の研究の流れは，記憶容量の問題の統計力学的解析です．
記憶容量とは，二値分類モデルが記憶できるランダムなデータの最大数（パラメータあたり）です．
記憶容量はモデルの表現能力の指標の一つであり，記憶容量が大きいほど，モデルは複雑な関数を表現することができると言えます．
記憶容量の問題は古くから統計力学的手法により研究されてきました．
近年では，活性化関数の選択が2層NNの記憶容量に与える影響を調べた研究 [1] があります．

2つ目の研究の流れは，無限幅NNとGauss過程あるいはカーネル法との関連に関するものです．
深層NNは様々なタスクにおいて非常に高い性能を発揮することが経験的にわかっていますが，その高い性能を理論的に説明することはまだ完全にはできていません．
無限幅NNをGauss過程として特徴づけるこの研究の流れは，NNの高い性能に対してより深い洞察を与える理論として注目されています．

これらの研究は独立に発展してきており，両者の関連性は今まで特に意識されていませんでしたが，本論文は，両者には深いつながりがあることを指摘します．無限幅2層NNの記憶容量を与える公式と，無限幅2層NNをカーネル法としてみたときのカーネルの値を与える公式に共通して現れる量に注目することで，記憶容量に関する結果をカーネルの性質として直観的に理解することが可能となりました．また，これらの異なる研究の流れの関連性がわかったことで，統計力学的手法の，NNの研究に対する応用が促進されることが期待されます．

背景

記憶容量の統計力学的解析

記憶容量の研究は1980年代のGardnerらの研究 [2,3] に遡ります．
Gardnerらは，パーセプトロンが記憶できるランダムなデータの個数をレプリカ法により計算しました．
レプリカ法は，スピングラス理論で開発された手法であり，大自由度のランダムな系の振る舞いを解析することができる強力な手法です．
データの個数を$P$，パラメータの数$N$として，$\alpha\coloneqq P/N<2$なら高い確率でパーセプトロンはデータを記憶でき，$\alpha > 2$なら高い確率でデータを記憶できないということがわかりました．
よって，パーセプトロンの記憶容量は$\alpha_c=2$であるということがわかりました．
Gardnerらの計算は，東北大学 大関真之教授のYouTube講義 [4] で紹介されています．

パーセプトロンの記憶容量が$\alpha_c=2$であるという事実は，Gardnerらの解析以前からCoverの定理 [5] として知られていましたが，Gardnerらの手法は，パーセプトロンに限らない様々なモデルに対して適用できる汎用性を持っているという点で優れています．

Gardnerらの枠組みに従って，レプリカ法で2層NNの記憶容量を計算する研究が1990年代に盛んに行われました．
木構造で活性化関数が符号関数の2層NNのパラメータあたりの記憶容量は，隠れ層の幅を$K$として，無限幅極限$K\to\infty$で発散することが明らかとなりました [6,7]．漸近的には，$\alpha_c\sim\frac{16}{\pi}\sqrt{\log K}$となります [8]．
また，全結合で活性化関数が符号関数の場合も，$K\to\infty$で記憶容量が発散することがわかりました．漸近的には$\alpha_c\sim\frac{16}{\pi-2}\sqrt{\log K}$となり，木構造の場合よりもパラメータあたりの記憶容量が定数倍大きくなっています [9]．
これは次のように直観的に説明できます．結合が木構造の場合は，それぞれの重みが異なる入力成分につながっているため，それぞれの重みは自分が担当している入力成分をすべて記憶しようとします．
一方で全結合の場合は，異なる重みが同じ入力成分につながっているため，それぞれの重みが異なる入力パターンを覚えるように「分業」することができます．
これによってそれぞれの重みの負担が減り，記憶容量が大きくなると考えられます．

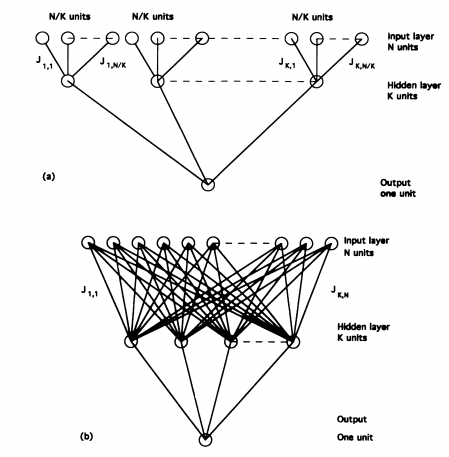
図1：2層NNのアーキテクチャ． (a) は木構造， (b) は全結合．図は [7] より

2層NNの記憶容量は，活性化関数$f$から定まる以下の関数の振る舞いで特徴づけられます．
$$
K_f(q) = \mathbb{E}\left[ f(x)f(y) \mid \begin{pmatrix}x \ y\end{pmatrix} \sim \mathcal{N}\left( \begin{pmatrix}0 \ 0\end{pmatrix}, \begin{pmatrix}1 & q \ q & 1\end{pmatrix} \right) \right]
\tag{1}
$$
この式の意味はすなわち次のとおりです．平均$0$，分散$1$，共分散$q$である2変量Gauss分布に従って2つの実数$x,y$をサンプルします．$q=0$ならば$x,y$は独立に値を取ります．$q$が$1$に近いほど，$x,y$は近い値を取ります．そして，サンプルされた$x,y$について，それらに$f$を適用した値の積$f(x)f(y)$の平均値が$K_f(q)$です．これは出力$f(x),f(y)$の類似度を表します．

直観的には，似ているものを区別する能力が高いほど，モデルの分類能力が高くなり，記憶容量が大きくなりそうです．言い換えると，$q$が$1$に近いときに$K_f(q)$の値が小さければ，活性化関数$f$が似ている入力を引き離す能力が高いと言え，記憶容量が大きくなりそうです．

いくつかの具体的な活性化関数$f$に対して，$1$に近い$q$に対する$K_f(q)$の値を見てみましょう．下図は，$q=0.99$の2変量Gauss分布に従ってサンプルされた入力$(x,y)$（左上）に対して，$(f(x),f(y))$の散布図を表示したものです．$f$としては，誤差関数$\operatorname{erf}，\operatorname{ReLU}，符号関数\operatorname{sgn}$を用いました．
どの活性化関数を用いても，$f$を適用することで入力の相関が少し小さくなっていることがわかります．$\operatorname{erf}$と$\operatorname{ReLU}$を比較すると，$\operatorname{ReLU}$のほうが若干$K_f(q)$の値が小さくなっています．
また，$\operatorname{sgn}$が最も相関を小さくする効果が大きいことがわかります．

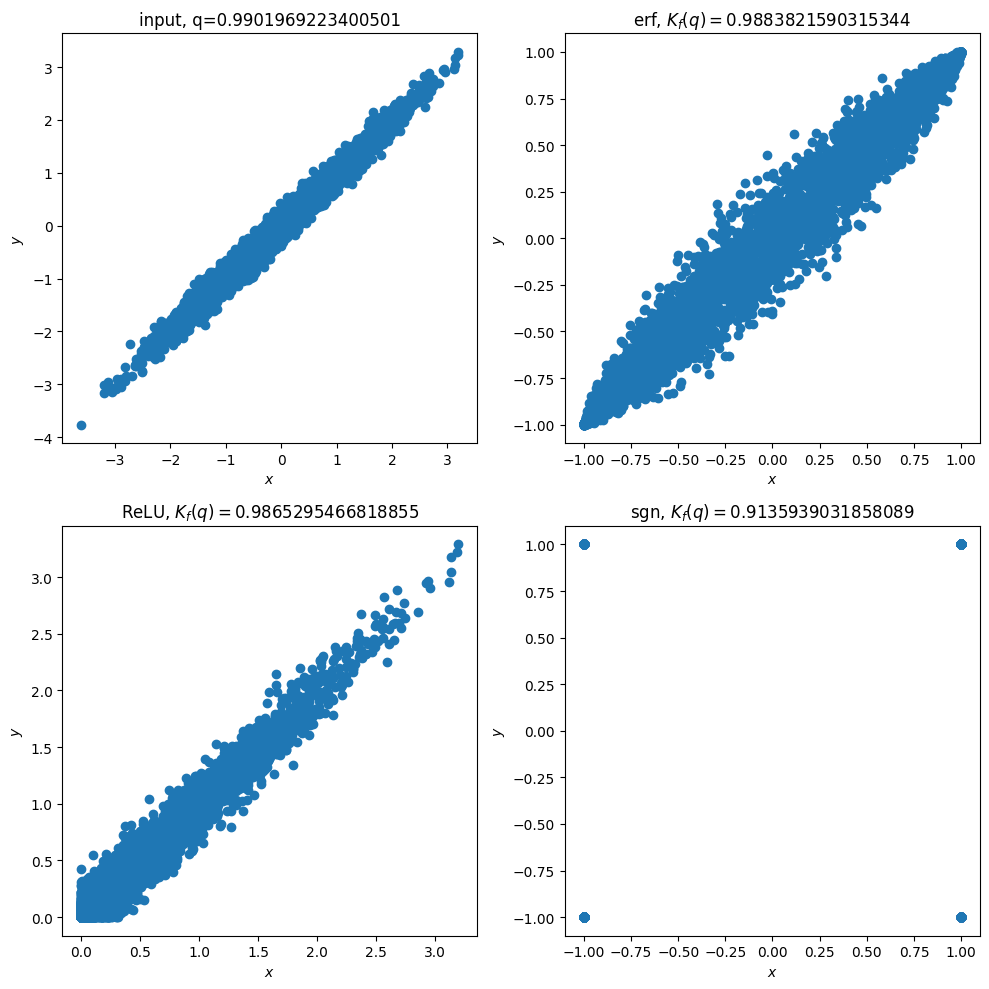
図2：いくつかの活性化関数 $f$ に対する $K_f(q)$ の値 ($q=0.99$)

次に，記憶容量の値を見てみましょう．[1] で報告されているパラメータあたりの記憶容量$\alpha_c$の値は，$f=\operatorname{ReLU}$に対して$\alpha_c\approx 2.934$，$f=\operatorname{erf}$に対して$\alpha_c\approx 2.451$です．また，$f=\operatorname{sgn}$に対しては，すでに述べたように記憶容量が発散するので$\alpha_c=\infty$です．

これらの例では，$q$が$1$に近いときに$K_f(q)$の値が小さいほど記憶容量$\alpha_c$が大きいという関係が成り立っていることがわかります．実は，この関係は常に成り立ち，木構造の2層NNの記憶容量は$\frac{d}{dq} K_f(q) \Big|_{q=1}$に比例することがわかっています [1]．

本節のまとめ

本節では，2層NNの記憶容量の統計力学的解析という研究の流れについて概説しました．
一般の活性化関数を持つ木構造2層NNの記憶容量を解析した研究によると，式(1)で定まる値$K_f(q)$が$q=1$付近で小さいときに記憶容量が大きくなることがわかりました．これは，活性化関数$f$が似ている入力を引き離す能力が高いほど，モデルの分類能力が高くなるという解釈ができることを述べました．

無限幅NNとGauss過程の対応

本節ではまずGauss過程とカーネル法について簡単に説明し，次に無限幅NNとGauss過程の関係について述べます．

Gauss過程とは，簡単に言うと無限次元ベクトルあるいは関数をランダムにサンプルできるGauss分布です．
機械学習でよく用いられる，例えばGauss分布やPoisson分布などの確率分布は，実数や有限次元ベクトルをサンプルする確率分布ですが，それを拡張したものになります．

Gauss過程の正確な定義は次のようになります．
関数$f: \mathcal{X} \to \mathbb{R}$ がGauss過程 $\mathcal{GP}(m,K)$ に従うとは，任意の有限個の入力の組 $\bm{x}=(x_1,\dots,x_n)^\top$ に対して，出力$(f(x_1),\dots,f(x_n))^\top$が多変量Gauss分布$\mathcal{N}(\bm{m}’, K’)$に従うことを言います．
ここで，平均を与える関数$m: \mathcal{X} \to \mathbb{R}$と共分散を与える関数$K:\mathcal{X}\times\mathcal{X}\to\mathbb{R}$を用いて，多変量Gauss分布の平均を$\bm{m}’=(m(x_1),\dots,m(x_n))^\top$，共分散行列の成分を$K’_{ij}=K(x_i,x_j)$と定めます．
関数$K$はカーネルとも呼ばれます．
$m,K$に選ぶ関数を色々変えることで，さまざまな形の関数を表現できます．以下の図3では，$\mathcal{X}=\mathbb{R},m=0$と3種類のカーネル$K$に対して，Gauss過程からサンプルされた関数をいくつか表示しています．
左の図はRBFカーネルというカーネルを用いたもので，滑らかな関数が得られています．真ん中の図で用いたカーネルを用いると，ギザギザした関数が得られます．右の図では2次の多項式カーネルを用い，2次関数が得られています．

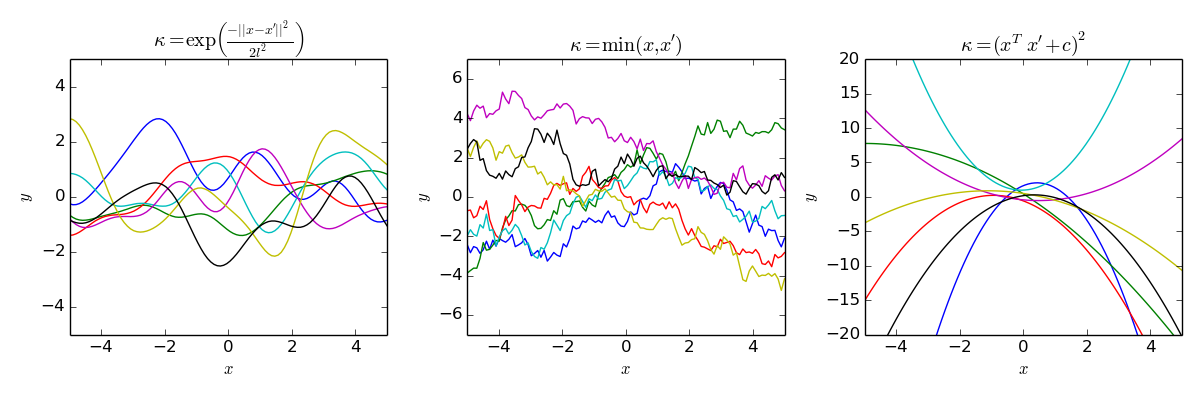
図3：いろいろなカーネルのGauss過程．出典 https://en.wikipedia.org/wiki/Gaussian_process

カーネル$K$の意味について詳しく考えてみましょう．
$K(x_i,x_j)$は，入力$x_i,x_j$に対する出力$f(x_i),f(x_j)$の類似度を測っているとみなせます．
カーネルの値が大きいほど，共分散が大きく，2つの出力は近い値を取ります．
一方で，カーネルの値が$0$に近いほど，共分散が$0$に近くなり，2つの出力はばらばらに独立な値を取ります．

Gauss過程を用いると，不確実性を考慮した回帰が行えます．
機械学習において，回帰問題は，データセット${(\bm{x}_i,y_i) \mid i=1,\dots,N}$が与えられたとき，このデータセットを出力する確率が最も高いような関数を見つける問題です．
すなわち，未知の関数$f$を用いて$y=f(\bm{x})+\epsilon$（$\epsilon$はノイズ）という式で$y$が生成されているとしたときに，与えられたデータセットから$f$を推定する問題です．
Gauss過程を用いた回帰はGauss過程回帰と呼ばれます．
Gauss過程回帰の説明は本記事では省略します．
また，Gauss過程回帰は，強力な回帰の手法であるカーネル法と深い関係にあります．
Gauss過程はカーネル法を拡張して不確実性を扱えるようにしたものと捉えられます．

無限幅NNの話に移ります．
一般にNNは多数の自由度を含み，その挙動を正確に捉えることは非常に難しい課題です．
しかし，幅を無限に大きくする極限では，様々な近似を施すことができ，理論的に扱いやすくなります．
近年，深層NNの複雑な挙動を理解するための理論的枠組として，無限幅NNの解析が大きな注目を浴びています．

無限幅NNの著しい性質の一つは，無限幅NNがGauss過程とみなせるという点です [12]．
2層のNNに対して，具体的に数式で見ていきましょう．
入力次元$d$，隠れ層の幅$N$，活性化関数$f$を持つ全結合2層NNを考えます．
重みとバイアスはGauss分布に従って独立に初期化します．
入力$\bm{x}\in\mathbb{R}^d$に対する出力$y(\bm{x})\in\mathbb{R}$は以下の式で表されます．
$$
y(\bm{x}) = \sum_{i=1}^N w_i^1 f(z_i(\bm{x})) + b^1 \
z_i(\bm{x}) = \sum_{j=1}^d w_{ij}^0 x_j + b^0_i
$$
重み$w_{ij}^0$は独立にサンプルされているので，${z_i}_{i=1,\dots,N}$は独立な確率変数です．
$y(\bm{x})$は独立な$N$個の確率変数の和であり，$N\to\infty$で中心極限定理により$y(\bm{x})$はGauss分布に従います．
すなわち，どのような$\bm{x}$に対しても出力はGauss分布に従うので，NNの初期化時には，$y(\bm{x})$はGauss過程であると言えます．
3層以上の深層NNでも，同様の議論により出力がGauss過程に従うことが示されます．

このNNとGauss過程の対応は，NN-GP（Neural Network-Gaussian Process）対応と呼ばれます．
層を深くするほど，対応するGauss過程のカーネルが複雑になるため，より複雑な関数を表現できるようになります．
このことを示したのが以下の図です．図4は，入力次元と出力次元が1のNNの重みをGauss分布に従って初期化したときの入出力の関係を表したものです．層を増すごとに，変化に富んだ複雑な関数が実現されていることがわかります．

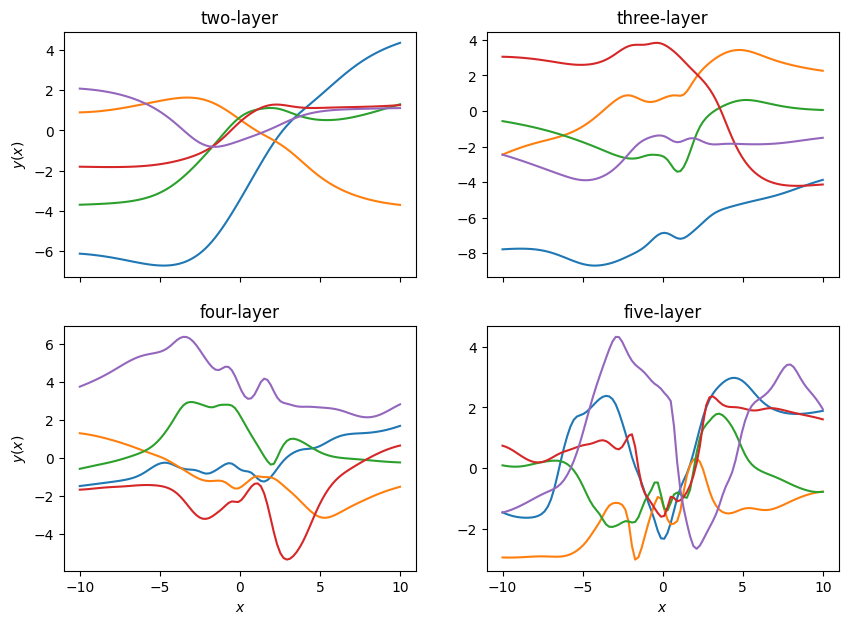
図4：2層から5層のNNに対応するGauss過程からのサンプル

無限幅2層NNに対応するカーネルを具体的に求めてみましょう．
簡単のため，バイアス$b^0,b^1$を無視し，重み$w^0,w^1$が従うGauss分布の平均を$0$，分散を$1$とします．
すると，カーネルは
$$
K(\bm{x},\bm{x}’)=\mathbb{E}[y(\bm{x})y(\bm{x}’)]=\mathbb{E}[f(z_1(\bm{x}))f(z_1(\bm{x}’))]
$$
となります．
さらに，$w^0$がGauss分布に従うことにより，$z_1(\bm{x})$もGauss分布に従います．
特に，$|\bm{x}|^2=d,q=\bm{x}^\top \bm{x}’/d$とすると，
$$
K(\bm{x},\bm{x}’)= \mathbb{E}\left[ f(z)f(z’) \mid \begin{pmatrix}z \ z’\end{pmatrix} \sim \mathcal{N}\left( \begin{pmatrix}0 \ 0\end{pmatrix}, \begin{pmatrix}1 & q \ q & 1\end{pmatrix} \right) \right]
\tag{2}
$$
と書くことができます．

この式は次のように理解することができます．$q$は2つの入力$\bm{x},\bm{x}’$の類似度を測っています．$q$が$1$に近いほど2つの入力は似ています．そして，$z_1(\bm{x}),z_1(\bm{x}’)$の類似度（正確には，積の期待値）も$q$になります．
$K(\bm{x},\bm{x}’)$は，2つの入力$\bm{x},\bm{x}’$に対する出力$y(\bm{x}),y(\bm{x}’)$の共分散すなわち類似度です．
共分散が小さいほど，出力はばらばらな値を取ることを思い出しましょう．
特に，$q$が$1$に近いときに，$K(\bm{x},\bm{x}’)$の値が小さければ，より変化に富んだ複雑な関数を表現することができるようになります．

本節のまとめ

本節では，Gauss過程について簡単に概要を述べ，NNがGauss過程とみなせるというNN-GP対応について説明しました．そして，2層NNに対応するGauss過程のカーネルは式(2)で与えられることを示しました．最後に，似た入力に対するカーネルの値が小さいほど，NNは急激に変化する複雑な関数を表現できることを説明しました．

2つの研究の共通点と相違点

記憶容量の統計力学的解析と，NN-GP対応という，2つの研究の流れを紹介しました．
これらの研究の共通点は明らかでしょう．式(1)と式(2)は全く同じであり，この値を通してこれらの研究の間の関係を理解することができます．

2層NNの記憶容量の研究では，式(1)の$q=1$付近での値が小さいほど，NNが同じ入力を引き離す能力が高く，記憶容量が大きくなるという結果が得られました．
一方，NN-GP対応の研究では，式(2)の$q=1$付近での値が小さいほど，似た入力に対する共分散を小さくすることができ，より変化に富んだ複雑な関数を表現できることがわかりました．

このように，記憶容量とNNの表現力は直接つながっているのです．この関係は，本記事で紹介している論文によって最初に指摘されました．

一方で，いくつかの相違点も述べておく必要があります．
記憶容量の統計力学的解析は，2層以下のアーキテクチャにとどまっており，3層以上の解析は難しいというのが現状です．また，入力次元も無限大に大きくする設定でのみ計算されています．
他方，NN-GP対応は3層以上の深層NNでも成り立ち，また入力次元も有限にとどめたまま解析が可能です．NN-GP対応の議論のほうが，より現実に近い設定を扱っていると言えます．

結論

本記事では，機械学習モデルの記憶容量の統計力学的解析という研究の流れと，NN-GP対応という研究の流れを説明しました．そして，これらの研究を無限幅2層NNに適用したときに共通に現れる$K_f(q)$という量を通じて，記憶容量の問題が，NNをGauss過程とみなしたときのカーネルの挙動として理解できることを説明しました．

この論文で指摘された，記憶容量とNN-GP対応の関係をきっかけに，統計力学と機械学習理論の間での知見や手法の共有が進むことが期待されます．

あとがき

余談として，筆者が現在取り組んでいる研究を紹介します．以下の内容の一部は，日本物理学会2024年春季大会で「一般の活性化関数を持つ全結合2層ニューラルネットワークの記憶容量」と題して発表しました．

2層NNの記憶容量は，以下の3つの場合に求められていることを本記事で説明しました：

• 活性化関数が符号関数で，アーキテクチャが木構造
• 活性化関数が符号関数で，アーキテクチャが全結合
• 活性化関数が一般の関数で，アーキテクチャが木構造

次の自然なステップは，活性化関数が一般の関数で，アーキテクチャが全結合の場合の解析です．
2層NNの中では，この設定がもっとも現実に近いものであり，2層NNの中では実用的な立場から最も興味のあるものであると筆者は考えます．
そこで，筆者はこの設定における記憶容量の計算に取り組み，以下のような結果を得ました．

• 木構造の場合と同様に，無限幅極限で記憶容量は有限にとどまる
• 活性化関数が符号関数で全結合の場合と同様に，重みが分業することにより記憶容量が木構造の場合と比べて大きくなる
• 記憶容量の値は，$\frac{\langle f’^2 \rangle – \langle f’ \rangle^2}{\langle f^2 \rangle – \langle f \rangle^2 – \langle f’ \rangle^2}$と書ける．ここで，$\langle \cdot \rangle$は標準正規分布に関する期待値である．（木構造の場合には$\frac{\langle f’^2 \rangle}{\langle f^2 \rangle – \langle f \rangle^2}$と書ける）

このように，記憶容量の値は木構造の場合と異なっており，NN-GPカーネルとの直接の関連を見出すのは難しいです．しかし，NNの重みを独立に初期化するのではなく，同じ層の重みに負の相関を持たせて初期化したNNを考えることで，本記事で述べたような，記憶容量の値とNN-GPカーネルの値の関連を論じることができると考えます（このような重みの初期化のスキームに実用的な意義があるかはわかりません）．

また，3層以上のNNの記憶容量の解析と，そのNN-GPカーネルとの関係が，実用的にも理論的にも最も興味のある設定です．2層NNと同じように3層以上のNNをレプリカ法で解析できるかどうかは筆者には不明（少なくとも非常に大変であることが予想される）ですが，将来的に解決されることを期待しています．

参考文献

• [1] Zavatone-Veth, J. A., & Pehlevan, C. (2021). Activation function dependence of the storage capacity of treelike neural networks. Physical Review E, 103(2). https://doi.org/10.1103/PhysRevE.103.L020301
• [2] Gardner, E. (1988). The space of interactions in neural network models. Journal of Physics A: General Physics, 21(1). https://doi.org/10.1088/0305-4470/21/1/030
• [3] Gardner, E., & Derrida, B. (1988). Optimal storage properties of neural network models. Journal of Physics A: Mathematical and General, 21(1), 271–284. https://doi.org/10.1088/0305-4470/21/1/031
• [4] 大関真之の雑談方程式 – これって人生変えちゃう授業かも – (2021). 情報科学としての数理情報学【2021年度・東北大学】. https://www.youtube.com/playlist?list=PLsBJ3psEqyr8Vo4Ez-xVKkesc8ba9ezu_ (2024年2月13日閲覧)
• [5] Cover, T. M. (1965). Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition. In IEEE Transactions on Electronic Computers: Vol. EC-14 (Issue 3). https://doi.org/10.1109/PGEC.1965.264137
• [6] Engel, A., Köhler, H. M., Tschepke, F., Vollmayr, H., & Zippelius, A. (1992). Storage capacity and learning algorithms for two-layer neural networks. Physical Review A, 45(10). https://doi.org/10.1103/PhysRevA.45.7590
• [7] Barkai, E., Hansel, D., & Sompolinsky, H. (1992). Broken symmetries in multilayered perceptrons. Physical Review A, 45(6). https://doi.org/10.1103/PhysRevA.45.4146
• [8] Monasson, R., & Zecchina, R. (1995). Weight space structure and internal representations: A direct approach to learning and generalization in multilayer neural networks. Physical Review Letters, 75(12). https://doi.org/10.1103/PhysRevLett.75.2432
• [9] Xiong, Y., Kwon, C., & Oh, J. H. (1998). The storage capacity of a fully-connected committee machine. Advances in Neural Information Processing Systems.
• [10] Baldassi, C., Malatesta, E. M., & Zecchina, R. (2019). Properties of the Geometry of Solutions and Capacity of Multilayer Neural Networks with Rectified Linear Unit Activations. Physical Review Letters, 123(17). https://doi.org/10.1103/PhysRevLett.123.170602
• [11] Zavatone-Veth, J. A., & Pehlevan, C. (2021). Activation function dependence of the storage capacity of treelike neural networks. Physical Review E, 103(2). https://doi.org/10.1103/PhysRevE.103.L020301
• [12] Lee, J., Bahri, Y., Novak, R., Schoenholz, S. S., Pennington, J., & Sohl-Dickstein, J. (2018). Deep neural networks as Gaussian processes. 6th International Conference on Learning Representations, ICLR 2018 – Conference Track Proceedings.