文献情報
- タイトル:Traffic Signal Optimization in Large-Scale Urban Road Networks: An Adaptive-Predictive Controller Using Ising Models
- 著者:Inoue, D. et al.
- 書誌情報:IEEE Access, vol. 12, pp. 188739-188754, (2024).
- DOI: 10.1109/ACCESS.2024.3514162.
概要
渋滞を解消するような交通信号機の最適化は、ドライバーのストレス軽減やCO2削減量の削減という点において重要です。現在の日本では、定周期制御と交通感応制御という2つの方法を併用しています。交通感応制御ではリアルタイムに交通情報を取得し信号の状態を決定するため、高速な計算が求められており、量子アニーリングの活用が期待されています。量子アニーリングを活用したR. Shikanai らの先行研究では、曖昧なパラメタが存在し、モデル予測制御も導入されていません。本研究ではそのような曖昧なパラメータを除去し、モデル予測制御を組み込んだイジングモデルを提案します。シミュレーションはオープンソースのSUMOを使用し、札幌のマップと正方格子で実験を行いました。その結果、従来型の制御方法に比べて本手法は渋滞を緩和し、CO2排出量を25%削減することを確認しました。また、問題サイズが大きいほど本手法の効果が現れることが分かりました。マップ内に流入する車両数を変化させた実験では、急激に渋滞となる相転移が確認されましたが、サイズが大きい場合に限りその影響を抑えることができました。ソルバーの比較では、計算性能と計算速度のトレードオフを加味すると、QAが最も実用的であると考えられます。
先行研究
D-Waveマシンを利用した交通信号機の最適化に関する論文がいくつか存在します。それらとの違いを、著者はTable1のようにまとめています。注目したいのは、[3]との比較です。本論文では、適用可能な交差点は最大で十字路(多叉路は不可)であるものの、予測制御を行った点で[3]とは大きく異なります。SUMOを使用して実用可能性について検証する点は同様となっています。
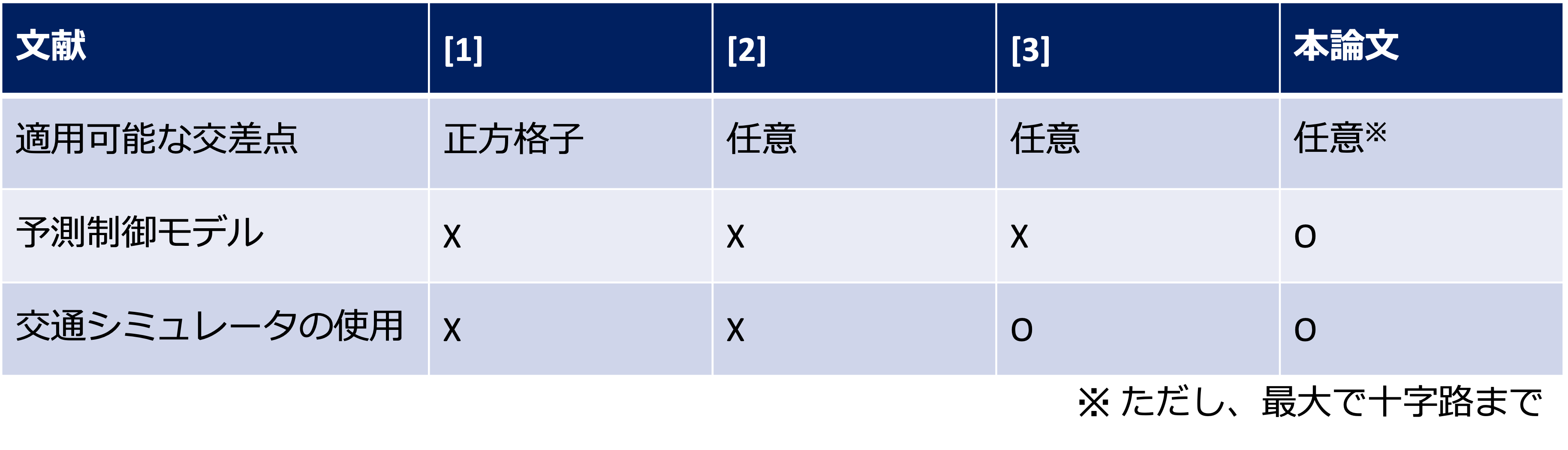
表1: 先行研究との比較 ([参考] https://arxiv.org/abs/2406.03690)
- [1] H. Hussain, M. B. Javaid, F. S. Khan, A. Dalal, and A. Khalique,‘‘Optimal control of traffic signals using quantum annealing,’’ Quantum Inf. Process., vol. 19, no. 9, p. 312, Aug. 2020.
- [2] A. Marchesin, B. Montrucchio, M. Graziano, A. Boella, and G. Mondo, ‘‘Improving urban traffic mobility via a versatile quantum annealing model,’’ IEEE Trans. Quantum Eng., vol. 4, pp. 1–13, 2023.
- [3] R. Shikanai, M. Ohzeki, and K. Tanaka, ‘‘Traffic signal optimization using quantum annealing on real map,’’ 2023, arXiv:2308.14462.
定式化
決定変数は、$\sigma_{i} = \pm 1$として、それぞれ交差点の2状態を表します。例えば、図1のように、$\sigma_{i} = +1$のとき東西方向が青信号、$\sigma_{i} = -1$のとき南北方向が青信号とします。今回は適用可能な交差点が「任意」であるため、$\sigma_{i} = +1$のとき南北方向が青信号でも構いません。
一方、$\sigma_{i}$の値によって、どの方向が通行可能になるのかを表すパラメタを準備しておくと便利です。そこで、$j \to i$方向に対して、$s_{ij}$という定数を以下のように定義します。
$$
\sigma_{i}s_{ij}= \begin{cases}+1 & \text {道路$(i,j)方向が進行可能$} \\ -1 & \text {道路$(i,j)方向が進行不可能$} \end{cases}
$$
例えば、図1のように、$\sigma_{i}=+1$で東西方向が青信号と定義していると、$s_{ij}=+1$と定まります。一方、$\sigma_{j}=-1$で南北方向が青信号と定義する場合は、$s_{kj}=+1$と定まります。このように、各$\sigma$において、「状態Aの時どちらの方向を青にするのか、状態Bの時どちらの方向を青にするのか」が定まれば、$s$というパラメータが自ずと決定されます。
図1: 決定変数の定義 ([引用] https://inspirehep.net/literature/2795460)
$$
\begin{align*}
x_{i}(t) &:= \text{(交差点$i$における方向Aの車両数) – (交差点$i$における方向Bの車両数)} \\
&:= 2\sum_{j\in N_{i}} \eta_{ij} s_{ij} q_{ij} \\
\end{align*}
\tag{1}
$$
ここで、$N_{i}$は交差点$i$に隣接する交差点の集合、$\eta_{ij}$は道路$(i, j)$の重みパラメタで、$q_{ij}$は道路$(i, j)$の車両数(詳細は後述)です。これにより、$x_{i}(t)>0$なら方向Aが混んでいるので、方向Aが青信号になるような$\sigma_{i}$にしよう、という方針が立てられるようになりました。
ここからは、未来の車両数を予測して$\vec{\sigma}$を決定できるような、予測制御モデルを組み込んでいきます。
まず、先程の$q_{ij}$を以下のように定義します。
$$
% \begin{align*}
q_{ij}(t) := \{\text{($道路(i,j)$に流入する割合[台/秒]) – ($道路(i,j)$から流出する割合[台/秒])}\}\times t \\ + \text{(元々、$道路(i,j)$にいた車両数)}
% \end{align*}
$$
これを時間$t$で微分すると、
$$
% \begin{align*}
\frac{d}{dt}q_{ij}(t) := \text{($道路(i,j)$に流入する割合[台/秒]) – ($道路(i,j)$から流出する割合[台/秒])}
% \end{align*}
\tag{2}
$$
となります。次に、流入・流出する割合を図2のように定義します。
図2: 道路$(i,j)$における流入・流出する割合 ([引用] https://inspirehep.net/literature/2795460)
$$
\begin{aligned}
& \frac{1}{2} a_{i j}^0\left(\sigma_j+1\right)+\frac{1}{2} a_{i j}^1\left(-\sigma_j+1\right)=\frac{1}{2}\left(\bar{a}_{i j}+a_{i j}^{\Delta} \sigma_j\right)
\end{aligned}
$$
ここで、$(\bar{a}_{i j}, a_{i j}^{\Delta})=(a_{ij}^0+a_{ij}^1, a_{ij}^0-a_{ij}^1)$としています。$a_{ij}^0$や$a_{ij}^1$は事前にシミュレーションして算出することを想定していますが、リアルタイムに計測することで急激な車両変化に対応することも可能になっています。流出割合も同様に定義します。
$$
\begin{aligned}
\frac{1}{2} o_{i j}^g\left(s_{i j} \sigma_i+1\right)+\frac{1}{2} o_{i j}^r\left(-s_{i j} \sigma_i+1\right)=\frac{1}{2}\left(\bar{o}_{i j}+o_{i j}^{\Delta} s_{i j} \sigma_i\right)
\end{aligned}
$$
$o_{ij}^r$は、右折/左折信号などを想定しています。これを式(2)に代入すると、以下のようになります。
$$
% \begin{align*}
\frac{d}{dt}q_{ij}(t) = \frac{1}{2}\left(\bar{a}_{i j}+a_{i j}^{\Delta} \sigma_j – \bar{o}_{i j}-o_{i j}^{\Delta} s_{i j} \sigma_i\right)
% \end{align*}
\tag{3}
$$
次に、式(1)に対して時間$t$で微分し、式(3)を代入すると、
$$
\begin{align*}
\frac{d}{dt}x_{i}(t) &= 2\sum_{j\in N_{i}} \eta_{ij} s_{ij} \frac{d}{dt}q_{ij} \\
&= \sum_{j\in N_{i}} \eta_{ij} s_{ij} \left(\bar{a}_{i j}+a_{i j}^{\Delta} \sigma_j – \bar{o}_{i j}-o_{i j}^{\Delta} s_{i j} \sigma_i\right) \\
&= -\sum_{j\in N_{i}}\eta_{ij}o_{i j}^{\Delta}\sigma_{i} + \sum_{j\in N_{i}}\eta_{ij}s_{ij}a_{i j}^{\Delta}\sigma_{j} + \sum_{j\in N_{i}}\eta_{ij}s_{ij}(\bar{a}_{i j} – \bar{o}_{i j}) \\
&= A_{ii}\sigma_{i} + \sum_{j\in N_{i}}A_{ij}\sigma_{j} + b_{i} \\
\end{align*}
$$
となります。$x_{i}$をベクトルで表記すると、以下のように表記できます。
$$
\begin{align*}
\frac{d}{dt}\vec{x}(t)
&= A\vec{\sigma}(t) + \vec{b} \\
\end{align*}
$$
ここで、$\tau$は信号機の切り替えを行うまでの時間$\tau$を導入します(例えば、60秒)。つまり、$t \le t’ \le t+\tau$の時間帯では、$\vec{\sigma}(t)$の状態が維持されるということです。この事実を利用すると、以下の差分方程式が得られます。
$$
\begin{align*}
\vec{x}(t+\tau) – \vec{x}(t)
&= \int_{t}^{t+\tau}\frac{d}{dt}\vec{x}(t’) dt’\\
&= \int_{t}^{t+\tau} (A\vec{\sigma}(t) + \vec{b}) dt’\\
&= (A\vec{\sigma}(t) + \vec{b}) ((t+\tau) – t)\\
&= (A\vec{\sigma}(t) + \vec{b})\times \tau \\
\end{align*}
$$
従って、
$$
\begin{align*}
\vec{x}(t+\tau)
&= \vec{x}(t) + A\tau\vec{\sigma}(t) + \vec{b}\tau\\
&= \vec{x}(t) + \tilde{A}\vec{\sigma}(t) + \tilde{b}\\
\end{align*}
$$
となります。このベクトルの内積を取ると、イジングモデルが得られます。しかし、本論文では、$\tau$よりも更に先の$2\tau, 3\tau, …$にも対応できるように一般化した以下のイジングモデルを提案しています。
$$
\begin{aligned}
& C\left(\sigma\left(\left[t, \ldots, t+\left(k_{\mathrm{h}}-1\right) \tau\right]\right)\right) \\
& \quad=\sum_{k=1}^{k_{\mathrm{h}}} \vec{x}(t+k \tau)^{\top} Q \vec{x}(t+k \tau),
\end{aligned}
\tag{4}
$$
ここで、$k_{h}$は何手先まで見通すかを表す整数値で、$Q$は交差点ごとの重みパラメタです。全ての交差点を平等に扱う場合は、$Q=I_{N}$(単位行列)とします。最後に、式(4)について式変形を行い、局所磁場項と相互作用項を明示的に表記していきましょう。まず、以下のように$\sigma, x$を拡張します。
$$
\begin{aligned}
\boldsymbol{\sigma}(t) & =\left[\vec{\sigma}(t)^{\top} \cdots \vec{\sigma}\left(t+\left(k_{\mathrm{h}}-1\right) \tau\right)^{\top}\right]^{\top} \in\{ \pm 1\}^{N k_{\mathrm{h}}}, \\
\mathbf{x}(t) & =\left[\vec{x}(t)^{\top} \cdots \vec{x}\left(t+\left(k_{\mathrm{h}}-1\right) \tau\right)^{\top}\right]^{\top} \in \mathbb{R}^{N k_{\mathrm{h}}} .
\end{aligned}
$$
さらに、以下のように行列とベクトルを定義します。
$$
\begin{aligned}
\mathbf{I} & =\left[\begin{array}{cccc}
I_N & I_N & \cdots & I_N
\end{array}\right]^{\top} \in \mathbb{R}^{N k_{\mathrm{h}} \times N}, \\
\mathbf{A} & =\left[\begin{array}{ccccc}
\tilde{A} & 0 & \cdots & \cdots & 0 \\
\tilde{A} & \tilde{A} & \ddots & & \vdots \\
\vdots & \ddots & \ddots & \ddots & \vdots \\
\tilde{A} & \tilde{A} & \cdots & \tilde{A} & 0 \\
\tilde{A} & \tilde{A} & \cdots & \tilde{A} & \tilde{A}
\end{array}\right]^{\top} \in \mathbb{R}^{N k_{\mathrm{h}} \times N k_{\mathrm{h}}}, \\
\mathbf{b} & =\left[\begin{array}{cccc}
\vec{\tilde{b}}^{\top} & 2 \vec{\tilde{b}}^{\top} & \cdots & k_{\mathrm{h}} \vec{\tilde{b}}^{\top}
\end{array}\right]^{\top} \in \mathbb{R}^{N k_{\mathrm{h}}} .
\end{aligned}
$$
これにより、差分方程式も以下のように拡張が可能です。
$$
\begin{aligned}
&\mathbf{x}(t+\tau)=\mathbf{I} x(t)+\mathbf{A} \boldsymbol{\sigma}(t)+\mathbf{b} .\\
\end{aligned}
$$
従って、イジングモデルは次のように局所磁場項と相互作用項、そして定数項に分けられます。
$$
\begin{aligned}
C & \left(\sigma\left(\left[t, \ldots, t+\left(k_{\mathrm{h}}-1\right) \tau\right]\right)\right) \\
& =\mathbf{x}(t+\tau)^{\top} \mathbf{Q} \mathbf{x}(t+\tau) \\
& =[\mathbf{I} x(t)+\mathbf{A} \boldsymbol{\sigma}(t)+\mathbf{b}]^{\top} \mathbf{Q}[\mathbf{I} x(t)+\mathbf{A} \boldsymbol{\sigma}(t)+\mathbf{b}] \\
& =\boldsymbol{\sigma}(t)^{\top} \mathbf{A}^{\top} \mathbf{Q A} \boldsymbol{\sigma}(t)+2[\mathbf{I} x(t)+\mathbf{b}]^{\top} \mathbf{Q A} \boldsymbol{\sigma}(t)+\boldsymbol{c},
\end{aligned}
$$
このイジングモデルを、シミュレーテッド・アニーリング(SA)や量子アニーリング(QA)で解くことにより、CO2排出量といった様々な指標について評価していきます。
実験
評価指標
本論文におけるイジングモデルは、$\vec{x}$の内積で表されました。つまり、各交差点で南北方向や東西方向の混雑度が同じくらいになって欲しい、というのが目的となっています。この混雑度の平準化は交通状況を直接的に評価している訳ではないため、以下の指標について評価を行います。
- Mean velocity: 道路ネットワーク内の全車両の平均速度
- Waiting vehicle ratio: 道路ネットワーク内の全車両に対する停止車両の割合
- CO2 emissions: シミュレータによって算出されるCO2排出量の総量
- Sum of squared vehicle bias: イジングモデルのエネルギー
比較する手法
比較する手法は以下の4つです。
- Local switching control : 局所的に以下の条件分岐で制御を行います。つまり、各交差点で(周りの交差点を気にせずに)進行できる車両が最も多い方向を青にします。
$$
\begin{cases}\sigma_i(t) \leftarrow+1 & \text { if } x_i(t)>0 \\ \sigma_i(t) \leftarrow \sigma_i(t-\tau) & \text { if } x_i(t)=0 \\ \sigma_i(t) \leftarrow-1 & \text { if } x_i(t)<0\end{cases}
$$ - Random control: 各交差点で、50%の確率で青信号、赤信号を切り替えます。
- Pattern control: あらかじめ決められた制御パターン(例えば、青信号40秒 ↔ 赤信号30秒)を繰り返します。初期状態については、以下の2つを考えます。
- Random pattern: 各交差点で初期状態をランダムに決定する。
- Coordinated pattern: 全ての交差点で同じ進行方向にする。(例えば、全ての交差点で東西方向を青信号にしておく)
札幌でのシミュレーション
まず、札幌においてシミュレーションを行います。道路ネットワークをOpenStreetMapに重ねて描画したのが図3です。いくつかのT字路を含んだ正方格子のようなネットワークになっています。
本シミュレーションでは、$\tau=60, k_{h}=1$と設定しています。
車両位置や目的地は一様分布で決定し、経路はSUMOのduarouterというツールで計算を行います。duarouterでは、道路の長さや制限速度、信号機の周期情報から最短経路が算出されます。
図3: 札幌の道路ネットワーク ([引用] https://inspirehep.net/literature/2795460)
本手法は、AMPIC(Adaptive Model Predictive Ising Controller)と名付けられています。図4は札幌における各評価指標の結果です。これより、全ての指標においてAMPICが他を上回ったことが分かります。そして、部分最適の”local”がそれに追従するような結果になっています。
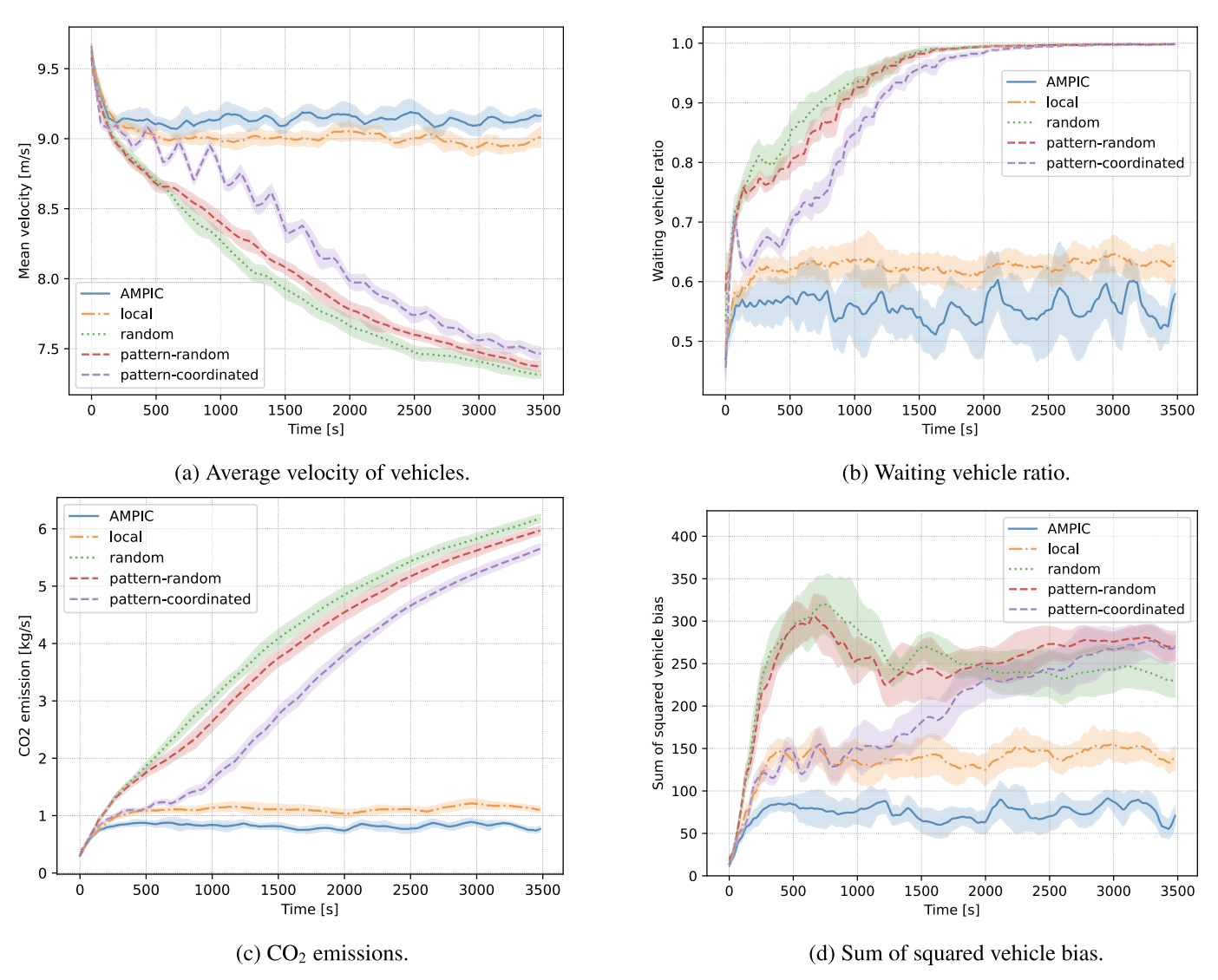
図4: 札幌における結果 ([引用] https://arxiv.org/abs/2406.03690)
AMPICであっても、ある一定以上の車両数に達すると渋滞発生が避けられず、手法の差異はなくなることが確認できます。
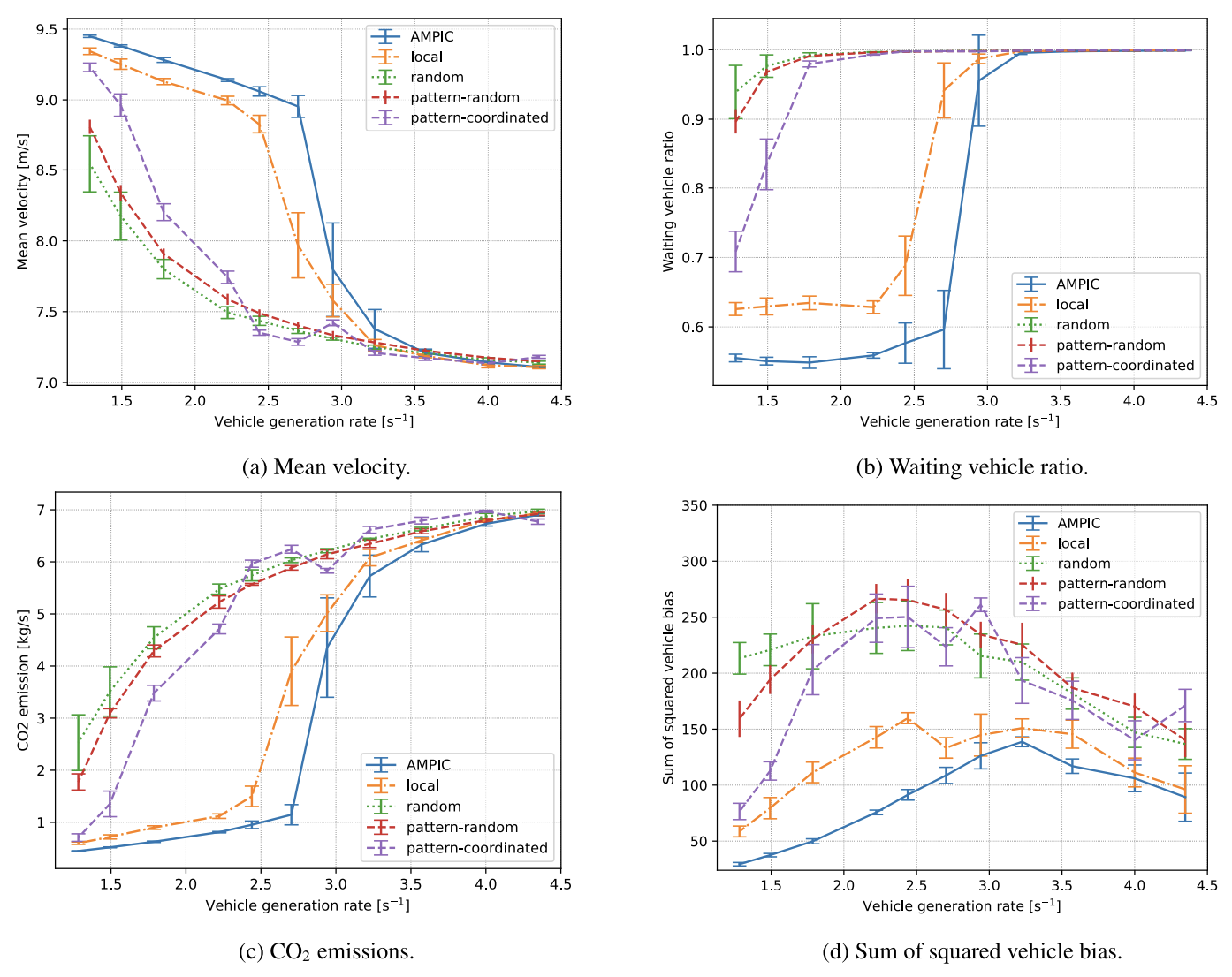
図5: 車両数を変化させた場合の結果 ([引用] https://arxiv.org/abs/2406.03690)
次に, $N \times N$の正方格子のマップを対象に、$N$の大きさを変化させて同様の実験を行います。図6(a)~(c)は, AMPICの結果です。横軸$\tilde{p}$は、マップの車両密度を公平にするために、車両発生率を$\sqrt{N}$で割ってスケーリングしています。つまり、$N$が大きいほど、たくさんの車両を発生させています。この結果から、マップサイズが大きいほど、AMPIC(全体最適化)の効果が現れやすくなることが分かります。これは、サイズが大きいほど組合せ数が多くなるためだと考えられます。
“local”手法に対するAMPICの結果(相対誤差)が図6(d)~(f)です。$\tilde{p}<0.3$の領域で、手法による差が顕著に現れています。そして、$\tilde{p} \approx 0.4$で急激な差が生じるのは、”local”でのみ渋滞が発生しているからです。それ以降の領域では、本手法も同様に渋滞が発生するため差が消滅していしまいます。
図6: 正方格子におけるAMPICの実験 ([引用] https://arxiv.org/abs/2406.03690)
続いて、何手先を見るのかを表す$k_{h}$を$1 \sim 10$で変化させて実験を行います。$10 \times 10$の正方格子で実験を行った結果が図7です。$k_{h}=6$までは順調に改善することを確認しましたが、それ以上では予測精度の悪化により交通状況の改善はわずかになることが分かります。
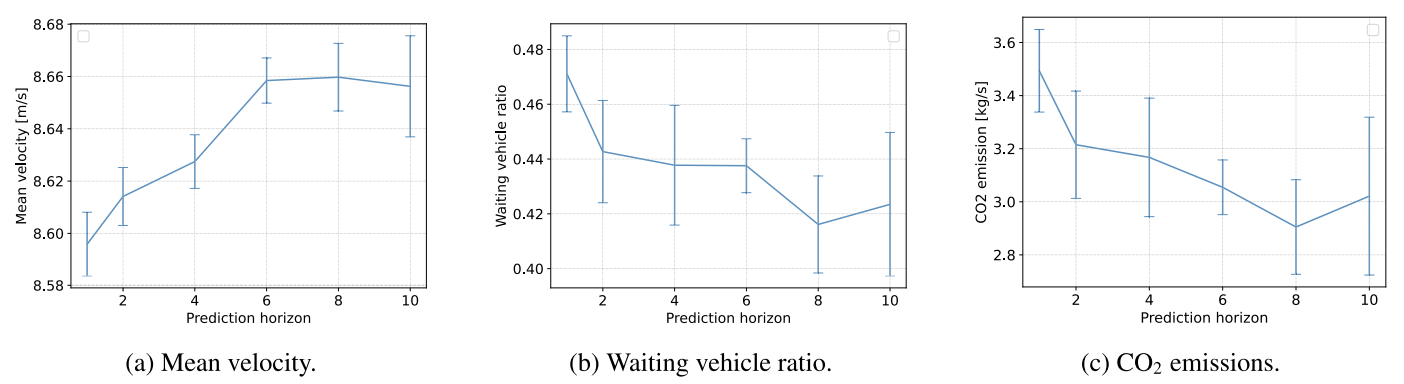
図7: $k_{h}$を変化させた場合の結果 ([引用] https://arxiv.org/abs/2406.03690)
最後に、計算手法による比較を行った結果が表2です。手法の詳細は以下の通りです。
- Greedy: 各ステップでエネルギーが最も低くなる変数をフリップしていく手法
- SA: シミュレーテッド・アニーリング (D-Wave neal)
- QA: 量子アニーリング (D-Wave Advantage)
交通状況に関する評価指標(表の上から3つ)において, SAが最も優位であることが分かります。一方、計算時間はQA(qpu_access_timeを計測)が圧勝しています。これらの結果から、計算性能と計算時間のトレードオフを考慮するとQAが最も実用的であると考えられます。ただし、SAは実行するマシンの性能により結果は変動すると述べられています。

表2: 各手法による比較 ([引用] https://arxiv.org/abs/2406.03690)
考察
図6では、ある一定の車両数を超えると一気に”渋滞状態”となる相転移が確認されました。通常の相転移は、サイズが大きいほど相転移の挙動が鋭く現れますが、今回はそれとは逆の結果となっています。つまり、大規模サイズほど本手法の効果が現れ、結果として転移が緩やかに生じたのだと考えられます。
あとがき
QAを利用した信号機最適化問題に関する論文はいくつか存在しますが、予測制御モデルをコスト関数に組み込んだのは画期的でした。一方で、図7のように、現時点のデータから予測された車両数でそこまで良い結果が得られるのは不思議でした。なぜなら、イジングモデルを設計するために必要な「道路の流出入割合」は、信号機の状態変化により大幅に変化すると考えられるからです。実用上では、最適化するタイミングで道路の車両数を計測して計算する、という逐次的な最適化が、急激な交通量変化に対応できるという点で優れていると思います。
本記事の担当者
鹿内怜央