バッチサイズが大きいとなぜ汎化性能が下がるのか？

Table of Contents

文献情報

タイトル: ON LARGE-BATCH TRAINING FOR DEEP LEARNING: GENERALIZATION GAP AND SHARP MINIMA
著者: Keskar, N. S. et al.
書誌情報: arXiv:1609.04836
出版年: 2017

概要

深層学習では計算効率を高めるために大規模バッチ学習（LB）が盛んに使われますが、経験的に「テスト精度が下がる」という問題が知られています。本論文では、その原因を「損失関数の谷の形状」という観点から探り、数値実験を通してLBが鋭い谷に、小規模バッチ（SB）が平坦な谷に収束しやすいことを示します。さらに、両者の利点を活かすために提案された「ウォームスタート」の効果を紹介し、汎化性能をめぐる新たな理解と今後の課題について考察します。

背景

深層学習は、損失関数 $f(x)$ の値を最小化するパラメータ$x$を見つける問題です。この最小化のために、確率的勾配降下法（Stochastic Gradient Descent, SGD）が広く用いられています。SGDは、学習データ全体ではなく、ランダムに抽出した一部の小さなデータセット（ミニバッチ）を使って勾配を計算し、モデルのパラメータを更新する手法です。具体的には、各ステップ$k$で以下の更新式に従ってパラメータ$x$を更新します。

$$
x_{k+1} = x_k – \alpha_k \left( \frac{1}{|B_k|} \sum_{i \in B_k} \nabla f_i(x_k) \right) \quad
$$

ここで、記号 $\nabla$ (ナブラ)は勾配（gradient）を意味し、$\alpha_k$はステップサイズ(学習率)、$i$はデータ番号を表しています。この勾配法を繰り返すことで損失関数の谷底（最小値）を探します。しかし、SGDは一つ前の更新結果を使って次の更新を行う逐次的な計算であるため、並列化による大幅な高速化が難しく、特に大規模なモデルでは学習に非常に長い時間がかかってしまうという課題があります。バッチサイズを大きくする大規模バッチ(Large Batch, LB)学習では、1エポックにおけるパラメータ更新の回数が少ないため、小規模バッチ(Small Batch, SB)学習よりも比較的計算効率が高いとされています。しかし、バッチサイズが大きいと、モデルの汎化性能(未知のデータに対する性能)が低下してしまうという、トレードオフの関係があることが経験的に知られていました。本論文では、この「ラージバッチ学習における汎化性能の低下」という問題について、損失関数の幾何学的な形状という観点からその原因を解明します。

表1: バッチサイズによる特徴

バッチサイズ	計算効率	汎化性能
大規模(LB)	◯	✕
小規模(SB)	△	◯

汎化性能低下の原因

大規模バッチにより汎化性能が低下する原因はいくつか考えられてきましたが、本論文の著者らは「大規模バッチ(LB)法は損失関数の鋭い谷の最小解(Sharp Minimum)に収束する傾向がある」という考えを支持しています。図1に損失関数における鋭い谷と平坦な谷の概念図を示します。図のように、学習データで得られた関数(Training Function)と、テストデータで得られた関数(Testing Function)はわずかにズレていると考えられます。もし、学習で得られたパラメータがSharp Minimumであれば、Testing Functionで評価した際に評価値が急激に悪化し、これが汎化性能の低下を招きます。一方、パラメータがFlat Minimumであれば、Testing Functionで評価しても評価値はそれほど悪化せず、テストデータに対しても精度の高い結果が得られると考えられます。次のセクションでは、LB法で得られた解がSharp Minimumであることを数値実験により示していきます。

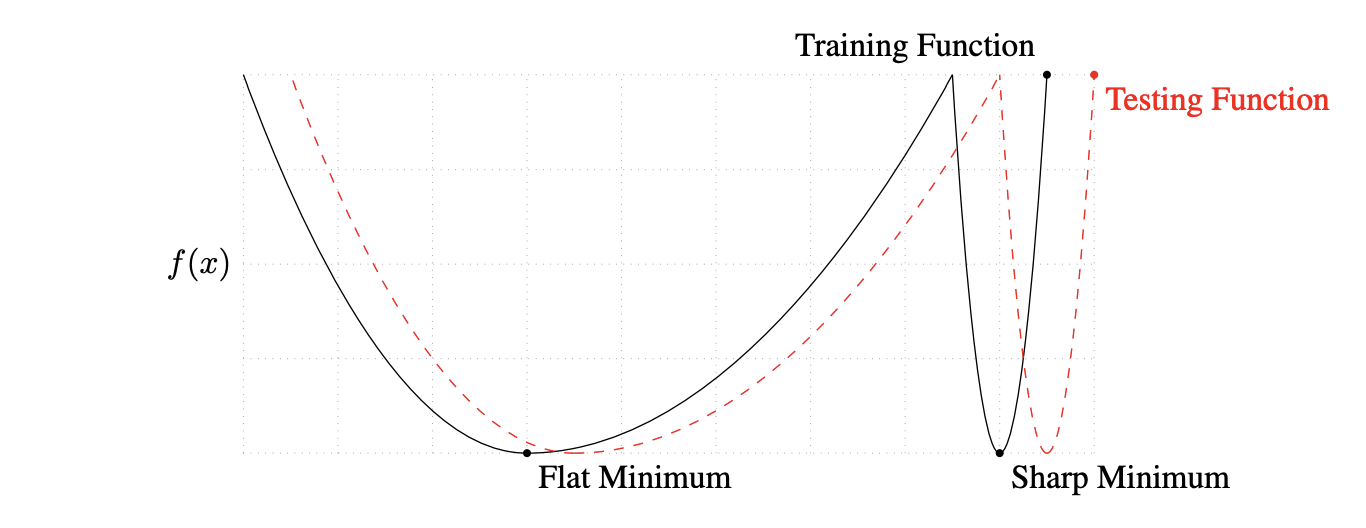
図1: 損失関数における鋭い谷と平坦な谷の概念図 (引用: https://arxiv.org/abs/1609.04836)

数値実験

ここでは、LB法で得られた解がSharp Minimumであることを示すために数値実験を行います。

SBとLBの汎化性能の評価

まず、LB法により汎化性能が低下することを示します。実験で使用する深層学習のネットワークは表2のとおりです。

表2: ネットワーク構成 (引用: https://arxiv.org/abs/1609.04836)

名前	ネットワークタイプ	データセット
$F_1$	全結合	MNIST
$F_2$	全結合	TIMIT
$C_1$	（浅い）畳み込み	CIFAR-10
$C_2$	（深い）畳み込み	CIFAR-10
$C_3$	（浅い）畳み込み	CIFAR-100
$C_4$	（深い）畳み込み	CIFAR-100

すべての実験において、LB法では学習データの10%をバッチサイズとして使用し、SB法では256個のデータをバッチサイズとしました。両手法でADAM(勾配法の計算方法の一種)を使用しました。すべての実験で異なる開始点(一様分布でランダム)から5回実施し、平均と標準偏差を表3に示します。学習データに対する精度はSB, LBともに高い値を示しています。一方、テストデータに関してはLBはSBよりも精度が低くなっており、汎化性能の低下が確認できます。このように、テストデータに対して極端に性能が悪化することをGeneralization Gapと呼びます。本論文の著者らは、Generalization Gapの原因は過学習によるものではないことを強調しています。通常、過学習ではピークに達した後、精度は減少していきますが、図2のように学習時の曲線は飽和していることが確認できます。

表3: 各ネットワークにおける小規模バッチ（SB）と大規模バッチ（LB）の性能
(引用: https://arxiv.org/abs/1609.04836)

名前	学習精度 (SB)	学習精度 (LB)	テスト精度 (SB)	テスト精度 (LB)
$F_1$	$99.66\% \pm 0.05\%$	$99.92\% \pm 0.01\%$	$98.03\% \pm 0.07\%$	$97.81\% \pm 0.07\%$
$F_2$	$99.99\% \pm 0.03\%$	$98.35\% \pm 2.08\%$	$64.02\% \pm 0.2\%$	$59.45\% \pm 1.05\%$
$C_1$	$99.89\% \pm 0.02\%$	$99.66\% \pm 0.2\%$	$80.04\% \pm 0.12\%$	$77.26\% \pm 0.42\%$
$C_2$	$99.99\% \pm 0.04\%$	$99.99\% \pm 0.01\%$	$89.24\% \pm 0.12\%$	$87.26\% \pm 0.07\%$
$C_3$	$99.56\% \pm 0.44\%$	$99.88\% \pm 0.30\%$	$49.58\% \pm 0.39\%$	$46.45\% \pm 0.43\%$
$C_4$	$99.10\% \pm 1.23\%$	$99.57\% \pm 1.84\%$	$63.08\% \pm 0.5\%$	$57.81\% \pm 0.17\%$

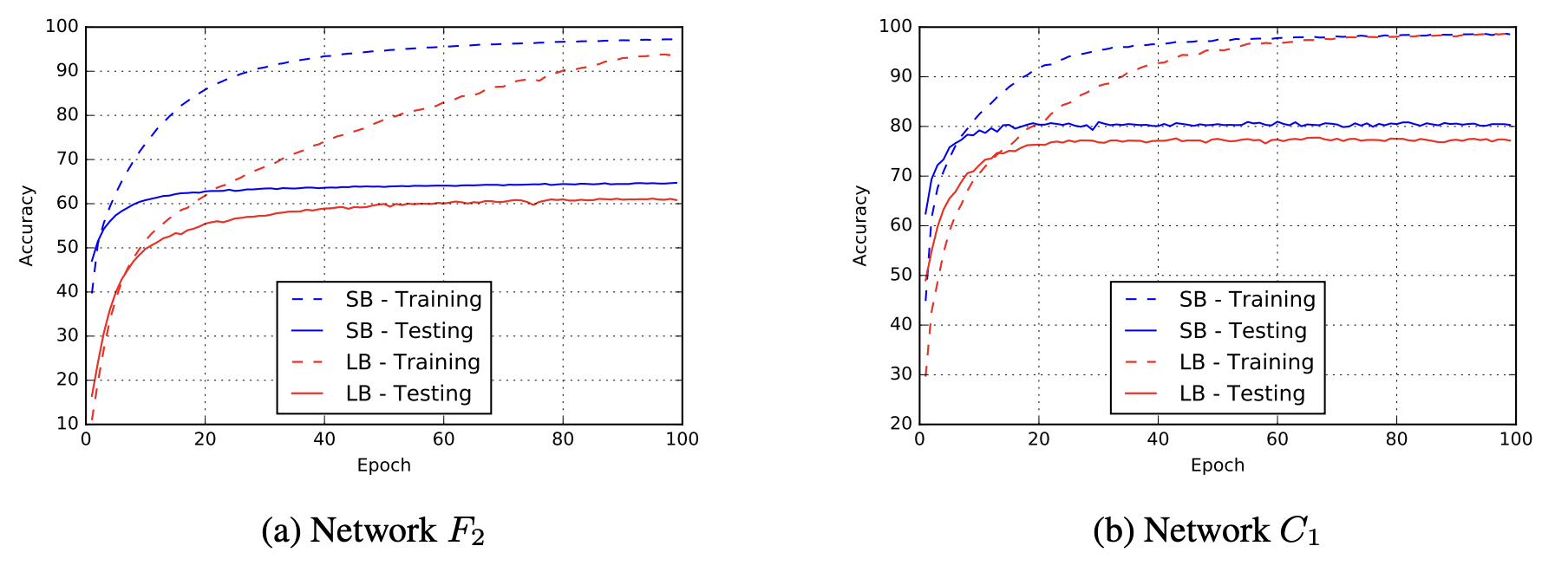
図2: 各エポックにおけるSBとLBの学習精度 (引用: https://arxiv.org/abs/1609.04836)

損失関数の断面図

本章では、前章で得られた解がどのように谷に位置しているのか可視化を行います。ここで、$x$は多次元であるため、そのままでは可視化することが困難です。そこで、SBとLBで得られた解をそれぞれ$x^{*}_{s}, x^{*}_{l}$とし、$f(\alpha x^{*}_{l} + ( 1-\alpha) x^{*}_{s})$をプロットすることで損失関数の断面図をプロットします。ここで、$\alpha \in [-1, 2]$の範囲を動きます。3次元の例を図3に示します。$\alpha x^{*}_{l} + ( 1-\alpha) x^{*}_{s}$は図の、$x^{*}_{s}, x^{*}_{l}$を結ぶ赤線で表現されており、この線における損失関数の断面図をプロットしたのが図4です。$\alpha=1$のLB解の付近では確かに鋭い谷になっており、$\alpha=0$のSB解の付近では平坦な谷になっていることが確認できます。

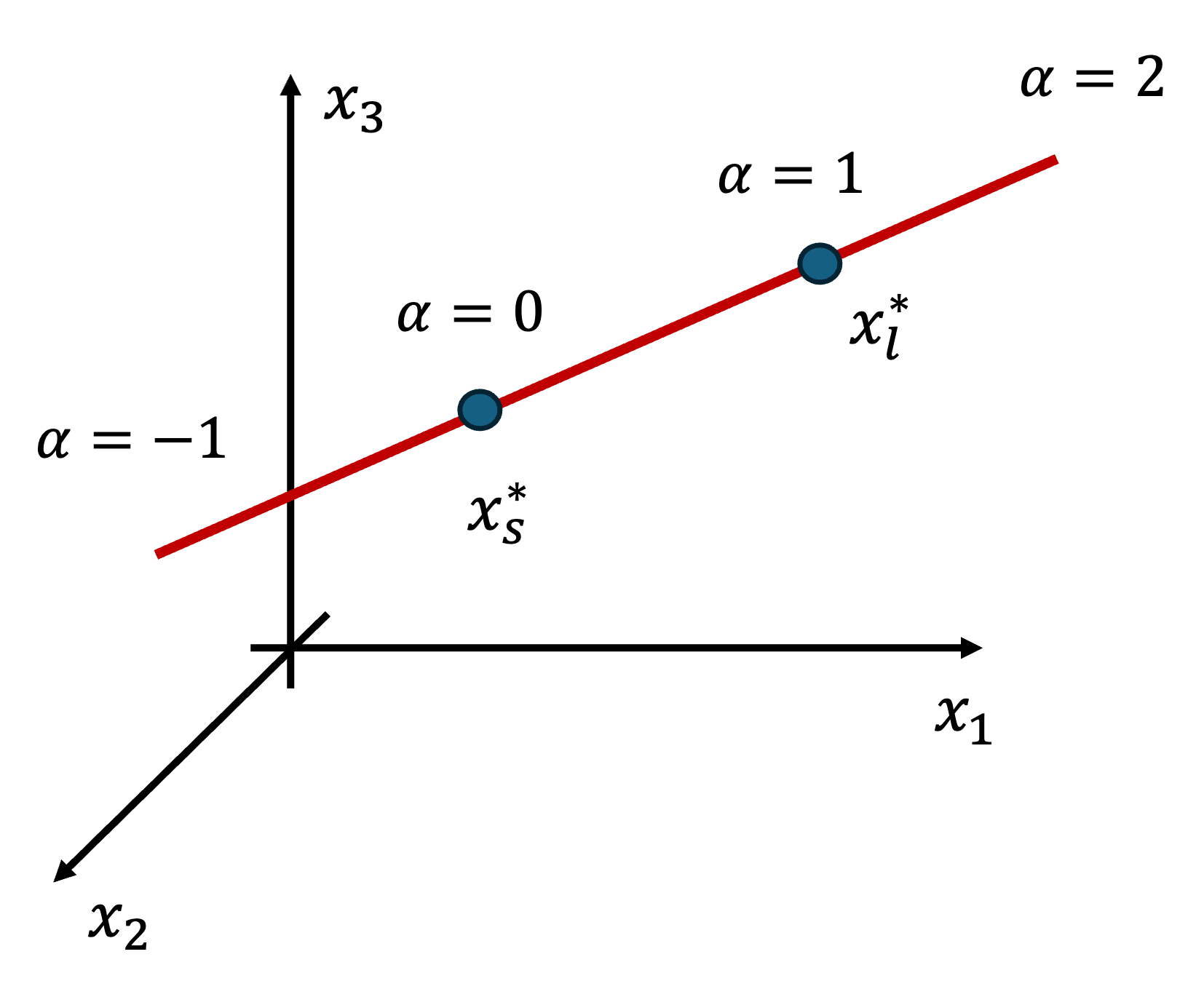
図3: 断面図の可視化の概要

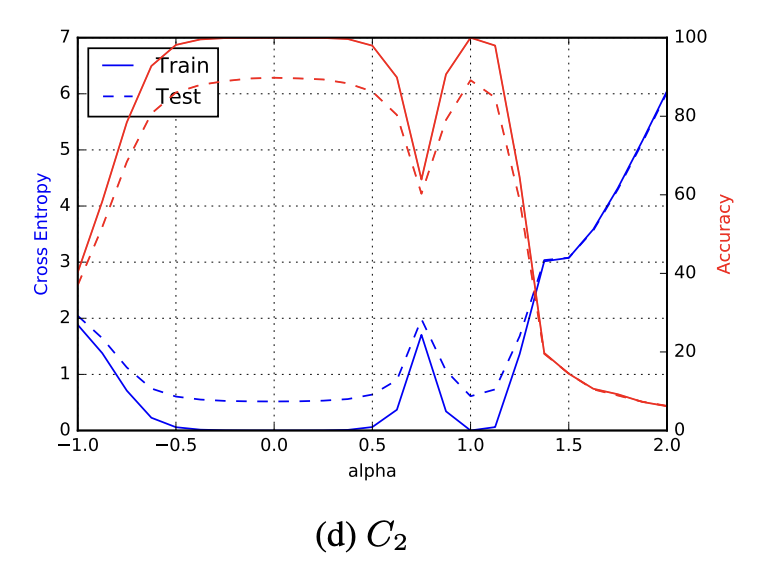
図4: 損失関数の断面図 (引用: https://arxiv.org/abs/1609.04836)

「谷の鋭さ」指標の導入

次に、「谷の鋭さ」を定量的に評価するための指標を導入します。通常、ヘッセ行列 $\nabla ^2 f(x)$の固有値と固有ベクトルを計算することで、$f(x)$の曲率(曲がり具合)を計算できるため、解が位置する谷の形状を評価できます。しかし、深層学習の損失関数は非凸であり非常に高次元であるため、ヘッセ行列を計算することが困難です。そこで、本論文では「谷の鋭さ」に関する以下の指標を提案しています。

指標:

$x \in \mathbb{R}^n$、$\epsilon > 0$、および$A \in \mathbb{R}^{n \times p}$が与えられたとき、$x$地点における$f$の鋭さを次のように定義します：

$$
% \begin{align*}
\phi_{x,f}(\epsilon, A) := \frac{\left(\max_{y \in \mathcal{C}_\epsilon} f(x+Ay)\right) – f(x)}{1+f(x)} \times 100
% \end{align*}
\tag{1}
$$

ここで、制約集合 $\mathcal{C}_\epsilon$ は次のように定義されます：

$$
% \begin{align*}
\mathcal{C}_\epsilon = \{ z \in \mathbb{R}^p : -\epsilon(|(A^+x)_i| + 1) \le z_i \le \epsilon(|(A^+x)_i| + 1) \quad \forall i \in \{1, 2, \dots, p\} \}
% \end{align*}
\tag{2}
$$

各式の説明は以下の通りです。

式(1): これは、解$x$から少し動いたときに($Ay$の分だけ動く)、関数の値がどれだけ急激に増加するかを計算しています。この値が大きいほど「鋭い谷」の底にいることを意味します。$A$は鋭さを計測する方向を格納した行列です。分母の+1は$f(x)$が0の時でも計算できるようにするためだと考えられます。
式(2): これは、式(1)で解の周りを探索する「範囲」を定義しています。$p$は探索する方向の次元数です。$\epsilon$がこの範囲の大きさを決めるパラメータで、大きいほど広い範囲を探索することを意味します。$A^{+}$は$A$の擬似逆行列です($A$が正方行列でないため)。$A^{+}x$とすることで高次元である$x$を$p$次元に射影し、各方向で鋭さを計測します。(ちなみに、次元削減をするだけなら$A^{+}$である必要はないですが、「$x$の大きさに応じた探索範囲」を定める、というスケーリングの役割も果たしています。)

それでは、これらの指標を用いた結果を表4・5に示します。表4では全空間に対して計測(つまり、$A=I_{n}$)を行い、2つの異なる範囲$\epsilon$の結果を示しています。表5ではランダムに100方向を選択し、同様の計測を行っています。これら2つの結果から、ランダム選択探索の場合に比べて全空間探索の方がSBとLBの差が大きく、また、全空間探索の標準偏差もLBが非常に大きいことが分かります。つまり、鋭い谷に位置していると考えられていたLB解ですが、周辺のほとんどは平坦な谷になっており、わずかな一部の急峻な方向が、この指標を大きくしていることが分かりました。次のセクションでは、どの程度のバッチサイズが適切であるのかについて実験を行います。さらに、なぜSB解が平坦に谷に落ちやすいのかについても議論します。

表4: 全空間における最小化点の鋭さ
(引用: https://arxiv.org/abs/1609.04836)

	ε=10^-3		ε=5 · 10^-4
	SB	LB	SB	LB
F₁	1.23 ± 0.83	205.14 ± 69.52	0.61 ± 0.27	42.90 ± 17.14
F₂	1.39 ± 0.02	310.64 ± 38.46	0.90 ± 0.05	93.15 ± 6.81
C₁	28.58 ± 3.13	707.23 ± 43.04	7.08 ± 0.88	227.31 ± 23.23
C₂	8.68 ± 1.32	925.32 ± 38.29	2.07 ± 0.86	175.31 ± 18.28
C₃	29.85 ± 5.98	258.75 ± 8.96	8.56 ± 0.99	105.11 ± 13.22
C₄	12.83 ± 3.84	421.84 ± 36.97	4.07 ± 0.87	109.35 ± 16.57

表5: 100次元のランダム部分空間における最小化点の鋭さ
(引用: https://arxiv.org/abs/1609.04836)

	ε=10^-3		ε=5 · 10^-4
	SB	LB	SB	LB
F₁	0.11 ± 0.00	9.22 ± 0.56	0.05 ± 0.00	9.17 ± 0.14
F₂	0.29 ± 0.02	23.63 ± 0.54	0.05 ± 0.00	6.28 ± 0.19
C₁	2.18 ± 0.23	137.25 ± 21.60	0.71 ± 0.15	29.50 ± 7.48
C₂	0.95 ± 0.34	25.09 ± 2.61	0.31 ± 0.08	5.82 ± 0.52
C₃	17.02 ± 2.20	36.03 ± 31.26	4.03 ± 1.45	86.96 ± 27.39
C₄	6.05 ± 1.13	72.99 ± 10.96	1.89 ± 0.33	19.85 ± 4.12

バッチサイズのしきい値と原因

問題のバッチサイズを増やすと、ある閾値からモデルの品質が低下することが知られています。図3では、２つのネットワークについて、バッチサイズを増やしたときのテスト精度と、解の鋭さについてプロットしています。$F_{2}$では約15000で、$C_{1}$では約500で急激に精度が減少し、それとは反対に谷の鋭さは上昇していることが確認できます。

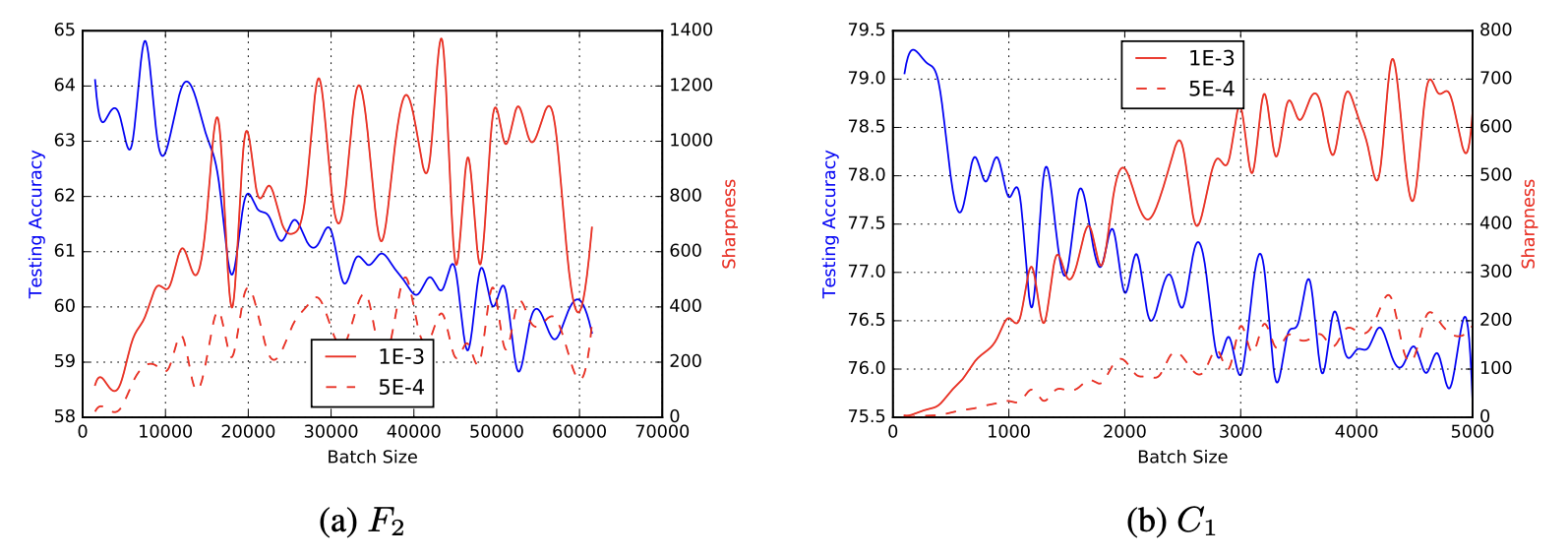
図5: バッチサイズにおけるテスト精度と谷の鋭さ

ここまでの実験から、SBによる学習の方が汎化性能が高いため、LBよりも優位だと考えるかもしれません。しかし、冒頭で説明したように、計算効率の面ではLBの方が優れています。そこで、次の実験では最初の数エポックをSBで学習し、その後LBで学習を行います(これをウォームスタートや、ピギーバックと呼んでいます)。結果は図6の通りです。横軸は、最初のSBで学習したエポック数を示しています。例えば、横軸20のラインは、「SB法で20エポック学習させた時点のモデル」の結果を意味します。青線の結果は、LBを実行する前のSBのみによる学習結果であり、ウォームスタートにより青線から赤線まで精度が向上したということを示しています。

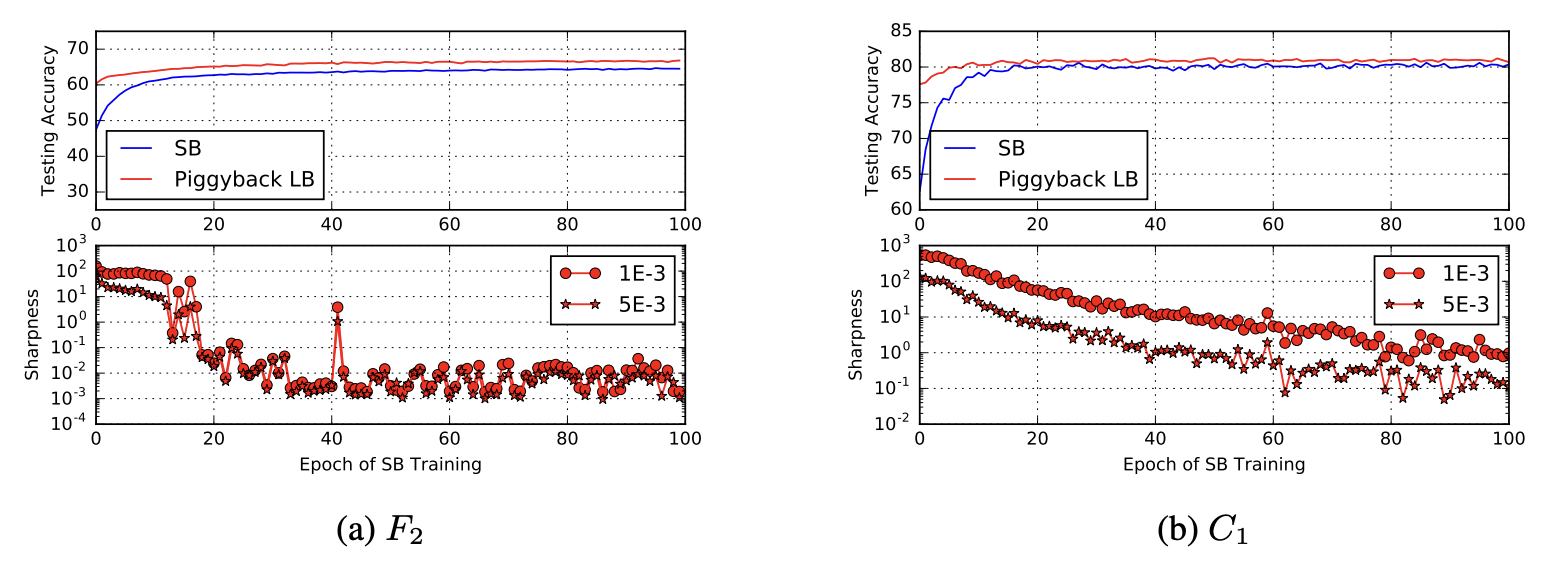
図6: ウォームスタートの実験 (引用: https://arxiv.org/abs/1609.04836)

ここで、ウォームスタートでSBを数エポックしか使用しない場合、LBによって汎化性能は向上しないことが分かっています。汎化性能が向上するのは、SBが探索を終えて平坦な最小化点を発見した後にLBを実行した場合だと考えられます。また、最小解とSB解、LB解の距離を計測すると、SB解はLB解より3~10倍遠い位置まで移動していることが分かっています。これらの結果から、SBでは勾配計算においてノイズが大きいため、鋭い谷にハマらず広範囲を探索できており、LBではノイズが小さいため、すぐ近くの鋭い谷に収束してしまうと考えられます。この考察を裏付けるための結果が図7です。横軸がクロスエントロピーになっており、右に行くほど学習が進んでいる状態を表します。(a)(b)ともに、学習が進むにつれ、LBはより鋭い谷へ、SBはより平坦な谷へ移動していることが分かります。

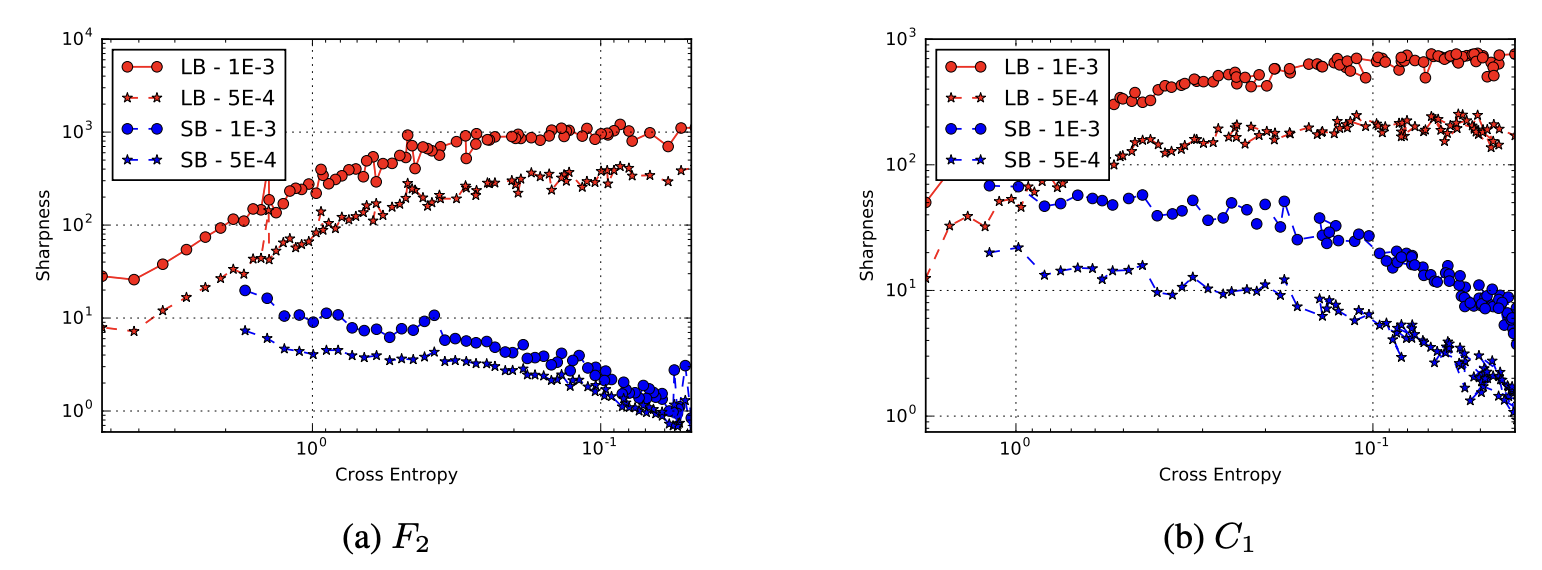
図7: クロスエントロピー(損失)に対する谷の鋭さ (引用: https://arxiv.org/abs/1609.04836)

考察・結論

本論文では、LBによる解が鋭い谷に位置することを数値実験により示しました。また、最初にSBを実行し、そのあとにLBを実行するといった、LBの計算効率を活かした手法の提案も行いました。しかし、現状では以下の課題が存在します。

LB法が深層学習の学習関数の鋭い最小化点に典型的に収束することを証明できるか？
『平坦な最小化点』と『鋭い最小化点』は、それぞれどれくらいの割合で存在するのか？
LB法の特性に適したニューラルネットワークアーキテクチャを設計できるか？
LB法が成功するようにネットワークを初期化できるか？
アルゴリズム的または正則化的な手段を通じて、LB法を鋭い最小化点から遠ざけることは可能か？

あとがき

最近では、D-Waveの量子アニーラが平坦な谷に落ちやすいことが注目されています。この現象についても理論的な証明は未だなされていませんが、本論文のSBと同様に、ノイズの影響によって鋭い谷に落ち込むことなく最小解を探索しているためではないかと示唆されます。さらに、SBからLBへ切り替える手法は、発想としてシミュレーテッド・アニーリングに極めて近く、機械学習分野と最適化計算分野が密接に関連していることを改めて感じさせます。

本記事の担当者

鹿内怜央

Post Views: 56