文献情報
- タイトル:Convergence Acceleration of Markov Chain Monte Calro-based Gradient Descent by Deep Unfolding
- 著者:Ryo Hagiwara, Satoshi Takabe
- 書誌情報(DOI):https://doi.org/10.7566/JPSJ.93.063801
概要
組合せ最適化問題の中には制約を持つ組合せ最適化問題が多く存在します。そのような制約付き最適化問題の解法として大関法と呼ばれる手法が知られています。大関法は、量子アニーリングやマルコフ連鎖モンテカルロ法のようなボルツマン分布からのサンプラーと勾配法を組み合わせた手法であり、サンプリングと勾配法によるボルツマン分布の更新を反復的に繰り返すアルゴリズムです。大関法によって得られる解の精度は、分布の更新の際に用いられるステップサイズと呼ばれるパラメータに大きく依存する一方、反復ごとのステップサイズの適切な調整は困難です。その問題に対処するために、本論文では深層展開と呼ばれる深層学習技術を大関法に適用しています。深層展開は、微分可能な処理によって構成される反復アルゴリズムの内部パラメータを深層学習によって最適化する技術です。大関法のステップサイズを深層展開によって最適化することにより、ステップサイズを一定値に固定した大関法に比べて解の収束が加速することを、幾つかの等式制約付き最適化問題を用いた数値実験により確認しています。この研究により、制約付き組合せ最適化問題のソルバーに対する深層展開の適用可能性が示されています。
背景
ここでは、大関法および深層展開の概要を説明します。大関法については本サイト内で解説記事が公開されている [1] ため、ここでは手法の理解に必要な説明に留めます。
大関法
大関法は、量子アニーリング(QA:Quantum Annealing)を用いて等式制約付き最適化問題を効率的に解くために、Ohzeki によって開発された手法です [2]。等式制約付き最適化問題は以下のように一般的に表現することができます。
$$
\tag{1}
\begin{aligned}
\min_{{\bm x}\in\{0,1\}^n} \quad & f_0({\bm x}) \\
{\rm s.t.} \quad & f_k({\bm x})=C_k \quad(k=1,\dots,m),
\end{aligned}
$$
ここで、目的関数 $f_0({\bm x})$ は変数 ${\bm x}\in\{0,1\}^n$ の1次または2次の関数であり、制約項 $f_k\ (k=1,\dots,m)$ は1次の関数です。QA は2次制約なし2値最適化問題(QUBO:Quadratic Unconstrained Binary Optimization)のみを解くことができるため、上述の問題を直接的に解くことはできません。等式制約を目的関数に含める形で表現する際には、以下のように罰金法を用いることが一般的です。
$$
\tag{2}
\begin{aligned}
L({\bm x};\lambda) = f_0({\bm x})+\lambda\sum_{k=1}^{m}\left(f_k({\bm x})-C_k\right)^2
\end{aligned}
$$
大関法では、上述のコスト関数 $L({\bm x};\lambda) $ に対応する分配関数 $Z=\exp\left(-\beta L({\bm x};\lambda)\right)$ に対してハバード・ストラトノヴィッチ変換を適用し、その過程で生じる補助変数 ${\bm \nu}\in R^{m}$ を以下の規則に基づき更新します。
$$
\tag{3}
\begin{aligned}
\nu_k^{(t+1)}=\nu_{k}^{(t)}+\eta_t \left(C_k – \langle f_k ({\bm x})\rangle_{Q({\bm \nu}^{(t)})}\right) \quad (t=0,1,\dots),
\end{aligned}
$$
ここで、ブラケット$\langle \cdot \rangle_{Q({\bm \nu}^{(t)})}$ は以下のボルツマン分布 $Q({\bm \nu}^{(t)})$ 上の期待値を表します。
$$
\tag{4}
\begin{aligned}
Q({\bm \nu}^{(t)})=\frac{1}{Z({\bm \nu}^{(t)})}\exp \left( -\beta\left(H({\bm x},{\bm \nu}^{(t)})\right)\right),
\end{aligned}
$$
ここで、$Z({\bm \nu}^{(t)})=\sum_{\{\bm x\}}\exp \left( -\beta\left(H({\bm x},{\bm \nu}^{(t)})\right)\right)$ です。また、ハミルトニアン $H({\bm x},{\bm \nu}^{(t)})$ は以下のように定義されます。
$$
\tag{5}
\begin{aligned}
H({\bm x},{\bm \nu}^{(t)})=f_0({\bm x})-\sum_{k=1}^{m}\nu_{k}^{(t)}f_k({\bm x})
\end{aligned}
$$
QA では、このハミルトニアンの最小化問題 ${\rm min}_{\bm x}H({\bm x},{\bm \nu}^{(t)})$ の解をサンプルセット $\{{\bm x}^{(t)}_1,{\bm x}^{(t)}_2,\dots,{\bm x}^{(t)}_S\}$ として取得し、そのサンプル平均 ${\bm x}^{(t)}_{\rm ave}=\frac{1}{S}\sum_{s=1}^{S}{\bm x}^{(t)}_{s}$ を用いることで更新則の $\langle f_k ({\bm x})\rangle_{Q({\bm \nu}^{(t)})}=f_k ({\bm x}^{(t)}_{\rm ave})$ を計算することができます。式 (2) の罰金法によるコスト関数では $f_k({\bm x})$ の2次項に起因する変数同士の2次相互作用が多く発生し、疎なハードウェアグラフを持つ QA マシンでは扱いにくいという問題点があります。一方、大関法におけるハミルトニアン $H({\bm x},{\bm \nu}^{(t)})$ は制約項が1次項であるため、QA マシンで扱いやすい形式になっています。
ただし、期待値 $\langle f_k ({\bm x})\rangle_{Q({\bm \nu}^{(t)})}$ はボルツマン分布 $Q({\bm \nu}^{(t)})$ からのサンプリングができれば計算できるため、QA ではなくマルコフ連鎖モンテカルロ法(MCMC:Markov-Chain Monte-Carlo)を用いることも可能であり、本論文では大関法を MCMC と勾配法を組み合わせた手法として利用しています。
しかし、式 (3) の更新則によって $\bm \nu$ について最大化する関数は困難な非凸関数であるため、大関法の収束速度と解精度はステップサイズ $\{\eta_t\}_{t}^{T-1}$ に大きく依存します。大関法の元論文 [2] では固定のステップサイズが用いられていましたが、反復ごとに調整されたステップサイズが適用されることが望ましいです。そこで、本論文ではステップサイズ $\{\eta_t\}_{t}^{T-1}$ の最適化に深層展開を適用しています。
深層展開
概要
深層展開は、勾配法をはじめとする微分可能な処理によって構成される反復アルゴリズムの内部パラメータを深層学習技術によって最適化する手法です。深層展開の概念図を以下に示します。
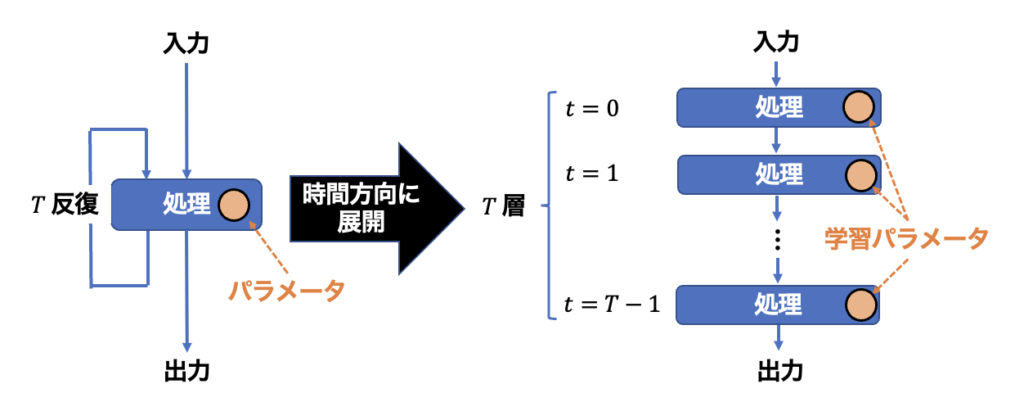
図 1:深層展開の概念図。
上図が示すように、深層展開では、何らかの処理を決められた回数(ここでは $T$ 回)繰り返すようなアルゴリズムを時間方向に展開します。そして、$t=1 \sim T$ 反復における内部パラメータを$T$層のニューラルネットワークとみなして学習します。学習の結果として、反復アルゴリズムの収束性の向上が期待されます。また、学習結果として得られるパラメータのスケジュールには解釈性があり、対象としている反復アルゴリズムでの最適なスケジューリング戦略の考察に役立てることができる場合があります。
勾配法への適用例
ここでは、勾配法を例として深層展開の適用方法を述べます [3]。勾配法によって微分可能な目的関数 $f({\bm x}):\ {\mathbb R}^n \rightarrow {\mathbb R}$ の最小化問題を解くことを考えます。このとき、勾配法の更新則は次のように記述することができます。
$$
\tag{6}
\begin{aligned}
{\bm x}^{(t+1)} = {\bm x}^{(t)} – \eta_t \nabla f({\bm x}^{(t)}), \ (t=0,1,\dots ,T-1),
\end{aligned}
$$
ここで、ステップサイズ $\{\eta_t\}_{t=0}^{T-1}$ は勾配 $\nabla f({\bm x})$ による更新の大きさを決めるハイパーパラメータです。勾配法の収束性は、このステップサイズのスケジュールに大きく依存します。そこで、このステップサイズ $\{\eta_t\}_{t=0}^{T-1}$ を学習パラメータとし、深層展開によって最適化することにします。図 1 の概念図と見比べると、勾配法における処理と学習パラメータはそれぞれ下図のように対応します。
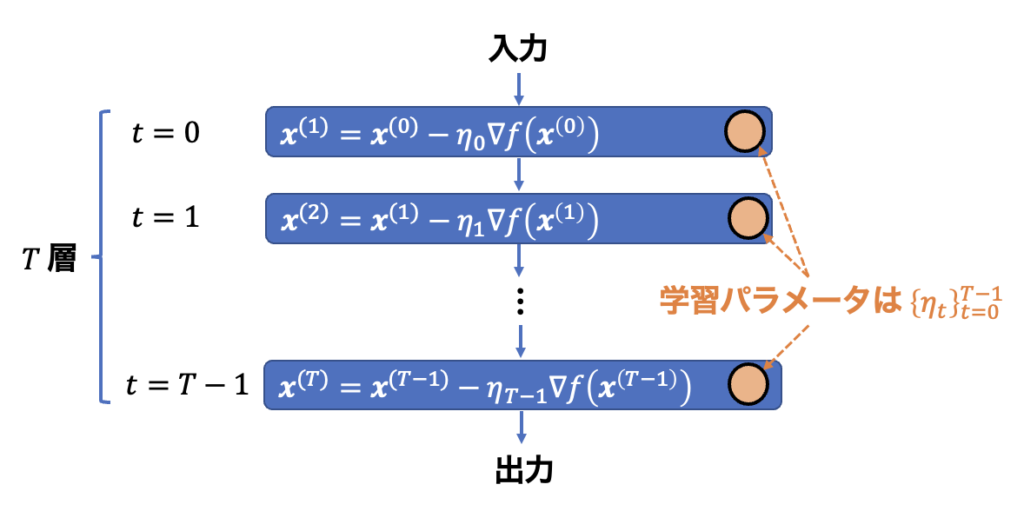
図 2:深層展開の勾配法への適用例。
対象とする問題
深層展開では、学習ベースでパラメータを最適化するため、学習のための訓練データセットと、学習結果を評価する検証データセットが用意されている必要があります。ここで言うデータとは、対象のアルゴリズムで解こうとしている問題のことです。よって、深層展開では、ある単一の最小化問題を解く、というよりも、ある構造を持つ最適化問題に対する平均性能を高めることを目的としています。例えば、勾配法で最小化する目的関数 $f({\bm x})$ が以下のように記述される場合を考えます。
$$
\tag{7}
\begin{aligned}
f({\bm x}) = \frac{1}{2}\left\| {\bm y}-A{\bm x}\right\|_{2}^{2}
\end{aligned}
$$
ここで、行列 $A\in\mathbb{R}^{m\times n}$ は定数行列です。そして、ベクトル ${\bm y}\in \mathbb{R}^{m}$ は確率 $N({\bm 0}, {\bm I})$ に従って生成されるものとします。このとき、ランダムな 1 つの ${\bm y}$ に対する $f({\bm x})$ の最小化問題が1つのデータとなります。${\bm y}$ をランダムに多数生成することでデータセットを作成し、深層展開によって勾配法のステップサイズ $\{\eta_t\}_{t=0}^{T-1}$ を学習した場合、そのステップサイズは「行列 $A$ の元でのランダムな最小二乗問題」に対して最適化されたものとなります。
また、訓練データとして$f({\bm x})$ の最適解 ${\bm x}$ を与えて学習する場合と、最適解を与えずに学習する場合とがあり、前者は「教師あり学習」と呼ばれ、後者は「教師なし学習」と呼ばれます。
学習の流れ
次に、深層展開による学習の流れを示します。学習プロセスは大まかに以下の 5 ステップに分けることができます。なお、ここでは勾配法を例として説明していますが、他の反復アルゴリズムであっても基本的には同様の学習プロセスが適用されます。
- 訓練データセットからデータを 1 つ取り出す
- 暫定的なステップサイズ $\{\eta_t\}_{t=0}^{T-1}$ によって勾配法を実行し、解 ${\bm x}$ を得る
- 解 ${\bm x}$ から損失関数 $L$ を評価する
- 損失関数の学習パラメータによる勾配 $\{\frac{\partial L}{\partial \eta_t}\}_{t=0}^{T-1}$ を求める
- 学習パラメータ $\{\eta_t\}_{t=0}^{T-1}$ を最適化する(ステップ 1. に戻る)
まず、ステップ 1. では、訓練データセットからデータを1つ取り出します。次に、ステップ 2. では、暫定的なステップサイズ $\{\eta_t\}_{t=0}^{T-1}$ を用いて $T$ 反復の勾配法を実行し、解 ${\bm x}$ を得ます。そして、ステップ 3. では、解 ${\bm x}$ をもとに学習がどれだけ成功しているかを損失関数 $L$ で評価します。損失関数は、教師あり学習の場合には最適解 ${\bm x}^{\ast}$ に対する誤差が用いられます。一方で、教師なし学習の場合には、問題設定に応じた指標が用いられます。今回の勾配法の例であれば、解 ${\bm x}$ に対する目的関数値 $f({\bm x})$ が用いられることがあります。続いて、ステップ 4. では、損失関数 $L$ の学習パラメータ $\{\eta_t\}_{t=0}^{T-1}$ による勾配 $\{\frac{\partial L}{\partial \eta_t}\}_{t=0}^{T-1}$ を求めます。この計算には誤差逆伝播法が用いられることが一般的です。そして、ステップ 5. では、$\{\frac{\partial L}{\partial \eta_t}\}_{t=0}^{T-1}$ を用いて学習パラメータ $\{\eta_t\}_{t=0}^{T-1}$ を最適化します。この最適化には Adam などの最適化アルゴリズムが用いられます。
以上のステップ 1. ~ 5. が、1 つの訓練データを用いた学習の流れになります。ステップ 5. で最適化されたステップサイズを用いて、新たな訓練データに対して再度ステップ 1. ~ 5. を繰り返すことで学習が進行します。損失関数が十分に小さくなったり、これ以上の改善が見込めなくなったりした時に学習を打ち切り、最終的な学習パラメータ $\{\eta_t\}_{t=0}^{T-1}$ を出力とします。
手法
3.1. 節で述べたように、大関法の収束速度はステップサイズに大きく依存しますが、その調整は困難です。その問題に対処するために、本論文ではステップサイズの最適化に深層展開を適用しています。論文中では、この提案手法をDUOM(Deep Unfolded Ohzeki Method)と読んでいます。図 2 に対応させる形で DUOM のイメージを表現したものを以下に示します。
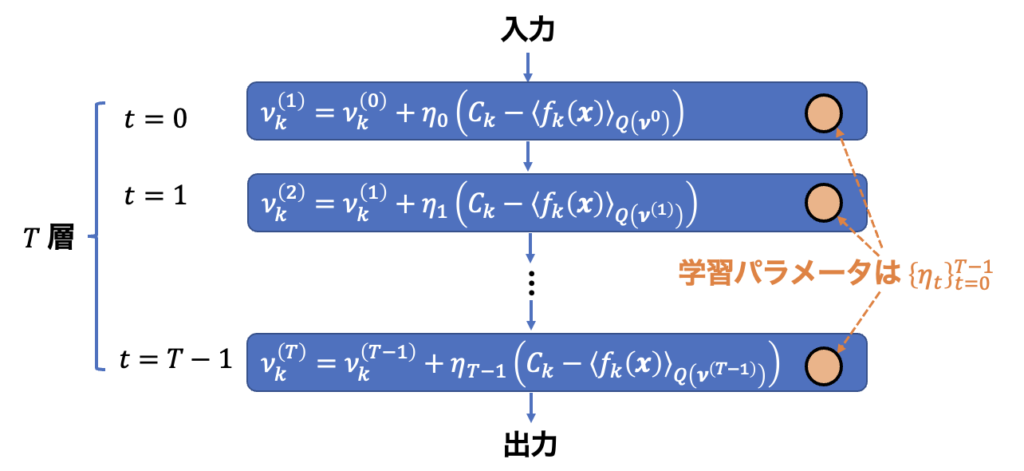
図 3:大関法への深層展開の適用(図 1 との対応関係)。
パラメータ $\{\eta_t\}_{t=0}^{T-1}$ の学習のためには損失関数 $L$ を定義する必要があります。本論文では、現実的な状況を想定し、対象とする等式制約付き組合せ最適化問題の最適解は与えられないものとします(教師なし学習)。したがって、損失関数として最適解に対する誤差を用いることはできません。そこで、本論文では以下のように損失関数 $L$ を定義しています。
$$
\tag{8}
\begin{aligned}
L \equiv \left\langle L({\bm x},\lambda )\right\rangle_{Q({\bm \nu}^{(T)})}
\end{aligned}
$$
これは、式 (2) で定義したコスト関数 $L({\bm x},\lambda )$ の最終反復 $T$ におけるサンプル平均を表します。よって、目的関数 $f_0({\bm x})$ の最小化と等式制約 $f_k({\bm x})=C_k$ の充足が同時に達成されたときに損失関数 $L$ は小さくなります。これにより、学習の成功度合いを表現することができます。
次に、学習パラメータ $\{\eta_t\}_{t=0}^{T-1}$ の最適化のために必要な損失関数の勾配 $\left\{ \frac{\partial L}{\partial \eta_t}\right\}_{t=0}^{T-1}$ について考える必要があります。各反復 $t$ における勾配 $\frac{\partial L}{\partial \eta_t}$ は誤差逆伝播法によって計算することができます。DUOM における誤差逆伝播法の連鎖率は以下のように記述されます。
$$
\tag{9}
\begin{aligned}
\frac{\partial L}{\partial \eta_t}=\sum_{k=1}^{m}\frac{\partial L}{\partial \nu_k^{(T)}}\left(\prod_{u=t+1}^{T-1}\frac{\partial \nu_k^{(u+1)}}{\partial \nu_k^{(u)}}\right)\frac{\partial \nu_k^{(t+1)}}{\partial \eta_t}
\end{aligned}
$$
例えば、制約数 $m=1$、総ステップ数 $T=5$ の場合、反復 $t=2$ における勾配 $\frac{\partial L}{\partial \eta_2}$ は以下のようになります。
$$
\tag{10}
\begin{aligned}
\frac{\partial L}{\partial \eta_2}=\frac{\partial L}{\partial \nu_1^{(5)}} \frac{\partial \nu_1^{(5)}}{\partial \nu_1^{(4)}} \frac{\partial \nu_1^{(4)}}{\partial \nu_1^{(3)}} \frac{\partial \nu_1^{(3)}}{\partial \eta_2}
\end{aligned}
$$
すなわち、損失関数 $L$ の ${\partial \nu_1^{(5)}}$(最終反復 $T=5$ における補助変数 $\nu_1^{(5)}$ による偏微分)から補助変数同士の偏微分へと連鎖し、最終的に反復 $t=2$ におけるステップサイズ $\eta_2$ による偏微分まで逆伝播します。共通する偏微分を約分していくと、分子に $\partial L$、分母に $\partial \eta_2$ が残り、所望の勾配に対応することが分かります。
次に、式 (9) に含まれる各偏微分を具体的に書き下すと、以下のようになります。
$$
\tag{10}
\begin{aligned}
\frac{\partial L}{\partial \nu_k^{(T)}}=\frac{\partial}{\partial \nu_k^{(T)}}\left\langle L({\bm x}, \lambda)\right\rangle_{Q({\bm \nu}^({T}))}
\end{aligned}
$$
$$
\tag{11}
\begin{aligned}
\frac{\partial \nu_k^{(u+1)}}{\partial \nu_k^{(u)}}=\frac{\partial}{\partial \nu_k^{(u)}}\left(\nu_{k}^{(u)}+\eta_u \left(C_k – \langle f_k ({\bm x})\rangle_{Q({\bm \nu}^{(u)})}\right)\right)=1-\eta_u\frac{\partial \langle f_k({\bm x})\rangle_{Q({\bm \nu}^{(u)})}}{\partial \nu_k^{(u)}}
\end{aligned}
$$
$$
\tag{12}
\begin{aligned}
\frac{\partial \nu_k^{(t+1)}}{\partial \eta_t}=\frac{\partial}{\partial \eta_t}\left(\nu_{k}^{(t)}+\eta_t \left(C_k – \langle f_k ({\bm x})\rangle_{Q({\bm \nu}^{(t)})}\right)\right)=C_k-\langle f_k({\bm x})\rangle_{Q({\bm \nu}^{(t)})}
\end{aligned}
$$
式 (10) および式 (11) には、期待値の微分が含まれていることが分かります。この期待値は、MCMC の微分不可能な処理(メトロポリス法の採択・棄却計算)を経て計算されることから、誤差逆伝播法に通常用いられる自動微分(損失関数値から、その勾配を機械的に求める方法。PyTorch では loss.backward() と記述することで自動的に微分処理が行われ、誤差逆伝播法が実行される)を適用すると学習に失敗してしまいます。しかし、これらの期待値の微分はさらに計算を進めることができ、その結果として自動微分の問題を回避できることが分かります。
まず、損失関数 $L$ の期待値の微分は以下のように計算されます(計算過程は付録に記載しています)。
$$
\tag{13}
\begin{aligned}
\frac{\partial}{\partial \nu_k}\langle L({\bm x}, \lambda)\rangle=\beta\left(\left\langle L({\bm x}, \lambda)\right\rangle \left\langle\frac{\partial H}{\partial \nu_k}\right\rangle – \left\langle L({\bm x}, \lambda)\frac{\partial H}{\partial \nu_k}\right\rangle\right)=\beta\left(\left\langle f_k({\bm x})L({\bm x}, \lambda)\right\rangle – \left\langle L({\bm x}, \lambda)\right\rangle \left\langle f_k({\bm x})\right\rangle\right)
\end{aligned}
$$
次に、制約項 $f_k({\bm x})$ の期待値の微分についても同様に以下のように計算されます。
$$
\tag{14}
\begin{aligned}
\frac{\partial \langle f_k({\bm x})\rangle}{\partial \nu_k}=\beta\left(\left\langle f_k({\bm x})\right\rangle \left\langle\frac{\partial H}{\partial \nu_k}\right\rangle – \left\langle f_k({\bm x})\frac{\partial H}{\partial \nu_k}\right\rangle\right)=\beta\left(\left\langle f_{k}^2 ({\bm x}) \right\rangle – \left\langle f_k({\bm x}) \right\rangle^2 \right)
\end{aligned}
$$
すなわち、期待値の微分は $\langle a \rangle \langle b \rangle – \langle a b \rangle$ という分散の形で記述できることが分かります。そしてこの分散は、大関法を $T$ 反復実行する過程(順方向計算)の結果から求めることができます。したがって、DUOM における誤差逆伝播法では、サンプリング結果から分散を推定することで、自動微分を回避することができます。パラメータの学習プロセス(逆方向計算)のために追加の計算が必要ない点は、サンプリングを応用した DUOM の特徴です。
以下の図 4 に、DUOM の全体像を示します。
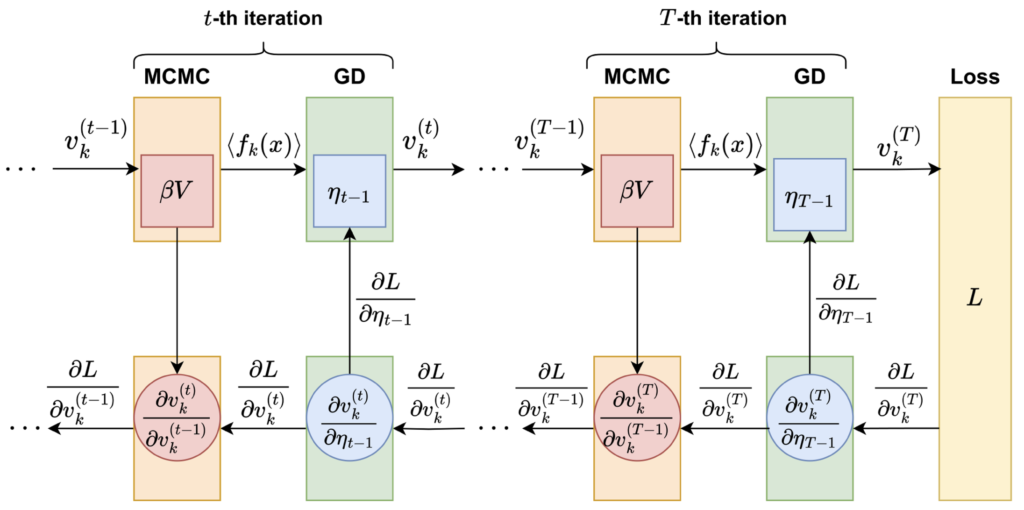
図 4:DUOM の全体像(DOI:https://doi.org/10.7566/JPSJ.93.063801)。
上図では、右に向かう矢印で順方向計算が表され、左に向かう矢印で逆方向計算が表されています。 $t$ 反復目に着目すると、MCMC によって得られた分散 $V$ が、逆伝播における連鎖率の計算に利用されることから下に矢印が伸びていることが分かります。また、勾配法(GD:Gradient Descent)におけるステップサイズ $\eta_{t-1}$ は、損失関数の勾配 $\frac{\partial L}{\partial \eta_{t-1}}$ を用いて最適化されることから上に矢印が伸びていることが分かります。
実験
ここでは、提案手法である DUOM の収束性を2つの最適化問題で検証した結果を示します。
K-minimum set 問題における検証
最初の例題は K-minimum set と呼ばれる問題で、以下のように定義されます。
$$
\tag{15}
\begin{aligned}
\min_{{\bm x}\in\{0,1\}^N} \quad & \sum_{i=1}^{N}h_i x_i \\
{\rm s.t.} \quad & \sum_{i=1}^{N}x_i =K,
\end{aligned}
$$
この問題は$N$ 個の数字の中から $K$ 個を選び,その和が最小になる数字の組合せを探す問題です。${\bm h}=(h_1 , \dots, h_N)$ が $N$ 個の数字のリストを表し、各 $h_i$ は標準正規分布からランダムに生成されます。式 (1) に合わせると $f_0 ({\bm x})=\sum_i h_i x_i$、$f_1 ({\bm x}) = \sum_i x_i , C_1 = K$ となります。K-minimum set においては $\bm h$ の小さい方から $K$ 個までの数字を足し合わせたものが $f_0 ({\bm x})$ の最適値です。
K-minimum set 問題における実験設定は以下の通りです:
- 問題パラメータ:$N=2000, K=50, \beta=1000$
- 訓練データ:ランダムベクトル ${\bm h}$
- 学習パッケージ:pytorch 2.0.0
- 学習方法:ミニバッチ学習
- ミニバッチの数は 50 個,各バッチのサイズは 5
- 学習パラメータの最適化手法:Adam Optimizer
- Adam の学習率は $ 5.0\times 10^{-6}$ から始めて更新ごとに $0.5$ 倍する
- DUOM の反復回数 $T=20$
- $\{\eta_t\}_{t=0}^{T-1}$ の学習前の初期値:全て $1.0×10^{-4}$
- MCMC からのサンプル数:100 個
以下の図 5 に、ステップサイズを固定した場合の大関法と DUOM とで、反復に対する残留損(residual loss)を比較した結果を示します。
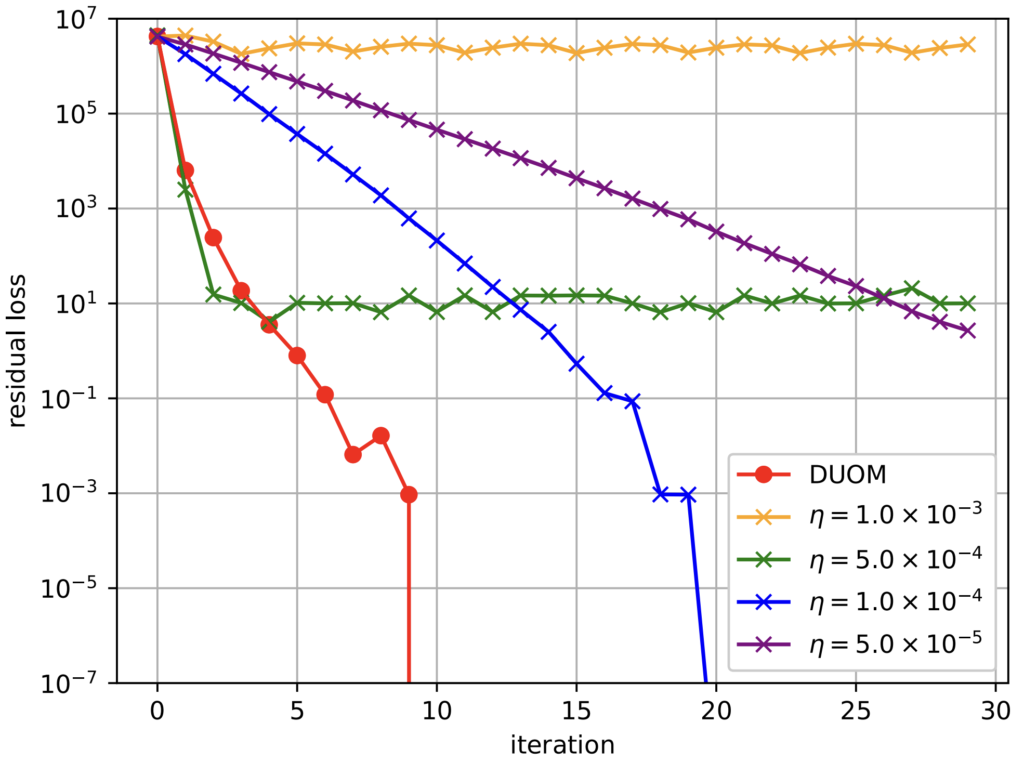
図 5:K-minimum set 問題における DUOM と $\eta$ を固定した大関法の比較結果。横軸は反復回数、縦軸は残留損を表す(DOI:https://doi.org/10.7566/JPSJ.93.063801)。
図 5 において、縦軸の残留損は、各反復における MCMC からのサンプル 100 個のうち最小の $L({\bm x};\lambda)$ と最適値 $L({\bm x}^{\ast};\lambda)$ との間の差を取ったものです。制約充足解の場合、$L({\bm x};\lambda)$ はペナルティ項がゼロになるため、最適値 $L({\bm x}^{\ast};\lambda)$ は目的関数値 $f_0({\bm x})=\sum_i h_i x_i$ の最適値と等しくなります。この実験では、固定する $\eta$ の値として 4 パターンを試していますが、DUOM はそのどれよりも少ない反復数で残留損がゼロになっていることが分かります。よって、DUOM は K-minimum set 問題において、$\eta$ を固定した大関法に比べて速く収束することが確認されました。
画像復元問題における検証
次に試す例題は画像復元の問題であり、以下のように定義されます。
$$
\tag{16}
\begin{aligned}
\min_{{\bm x}\in\{0,1\}^N} \quad & -\sum_{\langle i, j \rangle}x_i x_j \\
{\rm s.t.} \quad & y_k=\sum_{l=1}^{N}a_{k l}x_l \ (k=1,\dots , M) ,
\end{aligned}
$$
この問題は、観測行列 $A\in \mathbb{R}^{M\times N}$ と観測ベクトル $\bm y \in \mathbb{R}^{M}$ からサイズ $\sqrt{N}\times \sqrt{N}$ の元画像 ${\bm x}^{\ast}$ を復元する問題です。変数 $x_i\in\{0,1\}$ は $i$ 番目のピクセルの色(白 or 黒)を表し、${\langle i, j \rangle}$ は、画像で隣接するピクセルの組を表します。式 (1) に合わせると $f_0 ({\bm x})=-\sum_{\langle i, j \rangle}x_i x_j $、$f_k ({\bm x}) = \sum_{l=1}^{N}a_{k l}x_l , C_k = y_k$ となります。制約数 $M$ は観測行列の行数(=観測数)に対応します。
本実験で復元したい元画像 ${\bm x}^{\ast}$ を以下の図 6 に示します。
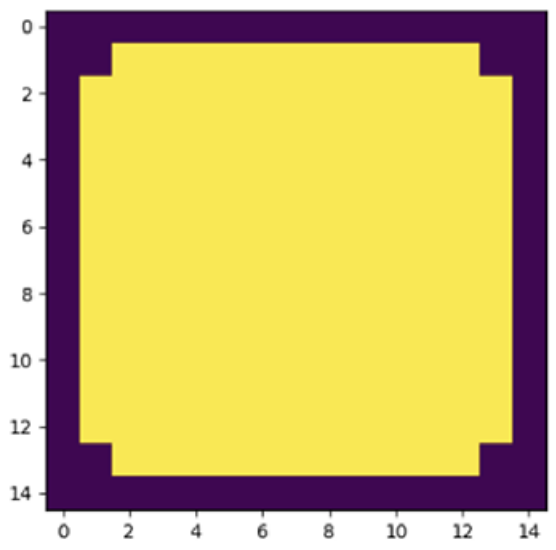
図 6:画像復元問題における復元対象の元画像(DOI:https://doi.org/10.7566/JPSJ.93.063801)。
$A=(a_{k l})$ の各要素 $a_{k l}$ は独立な標準正規分布からランダムに生成し、観測ベクトル $\bm y$ は $\bm y = A {\bm x}^{\ast}$ により求めます。画像復元問題における実験設定は以下の通りです:
- 問題パラメータ:$N = 15^2 = 225, M=135, \beta=10$
- 訓練データ:ランダム行列 $A$ および観測ベクトル $\bm y$
- 学習パッケージ:pytorch 2.0.0
- 学習方法:ミニバッチ学習
- ミニバッチの数は 20 個,各バッチのサイズは 8
- 学習パラメータの最適化手法:Adam Optimizer
- Adam の学習率は $5.0\times 10^{-3}$ から始めて更新ごとに $0.8$ 倍する
- DUOM の反復回数:$T=40$
- $\{\eta_t\}_{t=0}^{T-1}$ の学習前の初期値:全て $1.0×10^{-2}$
- MCMC からのサンプル数:100 個
以下の図 7 に、ステップサイズを固定した場合の大関法と DUOM とで、反復に対する平均二乗誤差(MSE:Mean Squared Error)を比較した結果を示します。
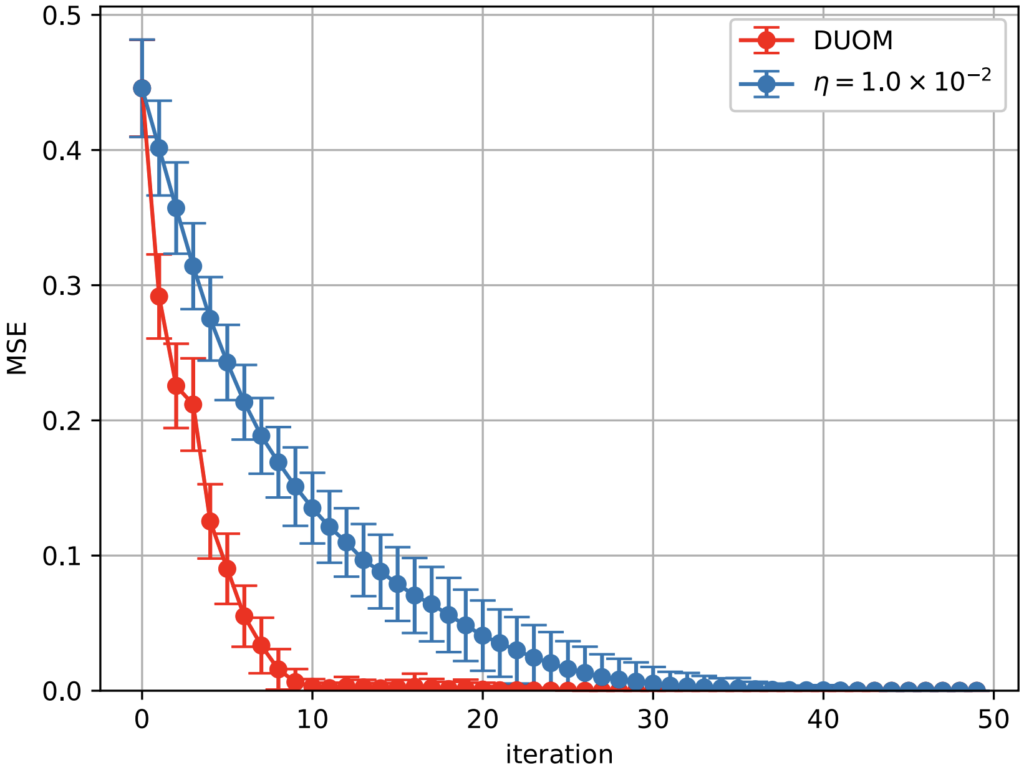
図 7:画像復元問題における DUOM と $\eta$ を固定した大関法の比較結果。横軸は反復回数、縦軸は平均二乗誤差を示す(DOI:https://doi.org/10.7566/JPSJ.93.063801)。
図 7 において、縦軸の MSE は厳密解 ${\bm x}^{\ast}$ に対する誤差の指標であり、$\sum_i (x_i – x_i^{\ast})^2 / N$ という式で表されます。解 $\bm x$ は、各反復における MCMC からのサンプル 100 個のうち $L({\bm x};\lambda)$ を最小にするものです。この実験では、固定する $\eta$ の値は適切に調整した上で、最も収束が速かった値 $\eta=1.0\times 10^{-2}$ を利用しています。この結果から、DUOM は $\eta$ を固定した大関法に比べて速くMSE がほぼゼロになっていることが分かります。また、$\eta$ を固定した大関法では、図 6 の元画像の復元に $32$ 反復を要した一方、DUOM は $11$ 反復で元画像が復元できました。よって、画像復元の問題においても、DUOM は $\eta$ を固定した大関法に比べて速く収束することが分かりました。
まとめ
本論文では、深層展開によって大関法のステップサイズを最適化する手法 DUOM を提案しました。K-minimum Set 問題と画像復元問題の2つの例題を用いた数値実験の結果から、ステップサイズが固定の大関法に比べて DUOM は収束速度が向上することが確認されました。この結果は、制約付き組合せ最適化ソルバーに対する深層展開の適用可能性を示しています。
今後の展望として以下の 2 点が挙げられます。1つ目に、DUOM のサンプラーを QA に変更することが考えられます。本論文ではボルツマン分布 $Q({\bm \nu})$ からのサンプラーとして MCMC を適用していますが、元々大関法は、QA マシン上で量子ビットを利活用することを目的として提案されたものであるため、DUOM に対する QA の適用は興味深い展望です(※)。2つ目に、他の等式制約付き最適化問題への DUOM の適用が考えられます。本論文で扱った問題以外にも、巡回セールスマン問題やグラフ分割問題など、等式制約付き最適化問題は多く存在するため、それらに DUOM を適用することで、提案手法の応用範囲を拡大することも重要な展望として挙げられます。
(※)本論文の著者らが、DUOM に対する QA の適用を検討した論文を 2025 年に公開しています [4]。この論文では、DUOM の学習プロセスには MCMC や Simulated Quantum Annealing(QA の古典的なシミュレーション手法)を使用し、学習されたステップサイズを用いて大関法を実行する際には QA を用いる、という転移学習を応用した手法を提案しています。転移学習とは、あるタスク向けに学習したモデルを、類似したタスクを実行するモデルに転用する学習方法を指します。よって、この論文では古典的なサンプラーにより学習した結果を QA (量子計算)に転用している点で、古典・量子転移学習を提案した論文として捉えることができます。
あとがき
式 (13), (14) にあるように、誤差逆伝播法においてサンプリングによる経験分散が活かせる点が興味深いと感じました。また、今回は提案手法をステップサイズ固定の大関法と比較していましたが、ステップサイズを調整するその他の手法(Optuna によるパラメータ推定や、動的にステップサイズを決定する勾配法の適用など)に比べて、深層展開の学習コストを加味しても利点があるのかどうかは気になりました。また、本論文により組合せ最適化問題のソルバーに対する深層展開の適用可能性が示されましたが、その他の組合せ最適化ソルバーにも深層展開が適用できないかを探っていきたいと思いました。
補足
式 (13) の導出過程を以下に示します。式 (14) についてもほとんど同様の計算で導出が可能です。
$$
\begin{aligned}
\frac{\partial}{\partial \nu_k} \langle L({\bm x}, \lambda)\rangle
& =\frac{\partial}{\partial \nu_k}\sum_{\{{\bm x}\}}L({\bm x}, \lambda)Q({\bm \nu}^{(u)}) \\
&=\frac{\partial}{\partial \nu_k}\sum_{\{{\bm x}\}}L({\bm x}, \lambda) \frac{1}{Z}\exp (-\beta H) \\
&=\sum_{\{{\bm x}\}}L({\bm x}, \lambda)\left( \exp (\beta H) \frac{\partial}{\partial \nu_k} \left(\frac{1}{Z}\right)+\frac{1}{Z}\frac{\partial}{\partial \nu_k}\left( \exp (-\beta H)\right) \right) \\
&=\sum_{\{{\bm x}\}}L({\bm x}, \lambda)\left( – \exp (\beta H) \frac{1}{Z^2}\ \frac{\partial Z}{\partial \nu_k} +\frac{1}{Z} \left(-\beta \frac{\partial H}{\partial \nu_k}\right)\exp (-\beta H)\right) \\
&=\sum_{\{{\bm x}\}}L({\bm x}, \lambda)\left(\beta \frac{\exp (-\beta H)}{Z}\sum_{\{{\bm x}\}}\left( \frac{\partial H}{\partial \nu_k}\frac{\exp(-\beta H)}{Z} \right)-\beta \frac{\partial H}{\partial \nu_k}\frac{\exp (-\beta H)}{Z} \right)\\
&=\sum_{\{{\bm x}\}}L({\bm x}, \lambda)\left(\beta Q({\bm \nu}^{(u)}) \sum_{\{{\bm x}\}}\left( \frac{\partial H}{\partial \nu_k}Q({\bm \nu}^{(u)}) \right)-\beta \frac{\partial H}{\partial \nu_k}Q({\bm \nu}^{(u)}) \right)\\
&= \beta\left( \sum_{\{{\bm x}\}}\left(L({\bm x}, \lambda)Q({\bm \nu}^{(u)})\right) \sum_{\{ {\bm x}\}}\left(\frac{\partial H}{\partial \nu_k}Q({\bm \nu}^{(u)})\right) – \sum_{\{{\bm x}\}}\left(L({\bm x}, \lambda)\frac{\partial H}{\partial \nu_k}\right)Q({\bm \nu}^{(u)}) \right)\\
&=\beta\left(\left\langle L({\bm x}, \lambda)\right\rangle \left\langle\frac{\partial H}{\partial \nu_k}\right\rangle – \left\langle L({\bm x}, \lambda)\frac{\partial H}{\partial \nu_k}\right\rangle\right)
\end{aligned}
$$
参考文献
-
D-Wave マシンの限界を超える”大関法”, /T-Wave/?p=6571
- M. Ohzeki, Sci. Rep. 10, 3126 (2020).
- 和田山正, モデルベース深層展開と深層展開, 森北出版 (2023).
- R. Hagiwara, S. Arai, S. Takabe, arXiv.2501.03518 (2025).