文献情報

• タイトル: Breaking limitation of quantum annealer in solving optimization problems under constraints
• 著者: Ohzeki, M
• 書誌情報: Sci Rep 10, 3126 (2020).
• DOI: https://doi.org/10.48550/arXiv.2201.04877

概要

現状のD-Waveマシンでは、ハードウェア上に解きたい問題のグラフを埋め込む必要があります。このグラフが密になればなるほど、使用できる量子ビット数は少なくなってしまいます。問題をQUBO形式で表現する際、制約を罰金項で記述することがよくあります。しかし、罰金項は2次項であるため必然的にグラフは密になってしまい、使用できる量子ビット数を少なくしてしまいます。本論文では、このようなD-Waveマシンを使用する際に生じてしまう制限を解消する方法を紹介します。この手法は、論文の著者にちなんで「大関法」と呼ばれています。

背景

量子アニーリングマシンであるD-Wave 2000Qでは、物理的な量子ビットはキメラグラフという独特な構造になっています。最適化問題を解く際には、図1のキメラグラフ上にマッピングを行う必要があります。

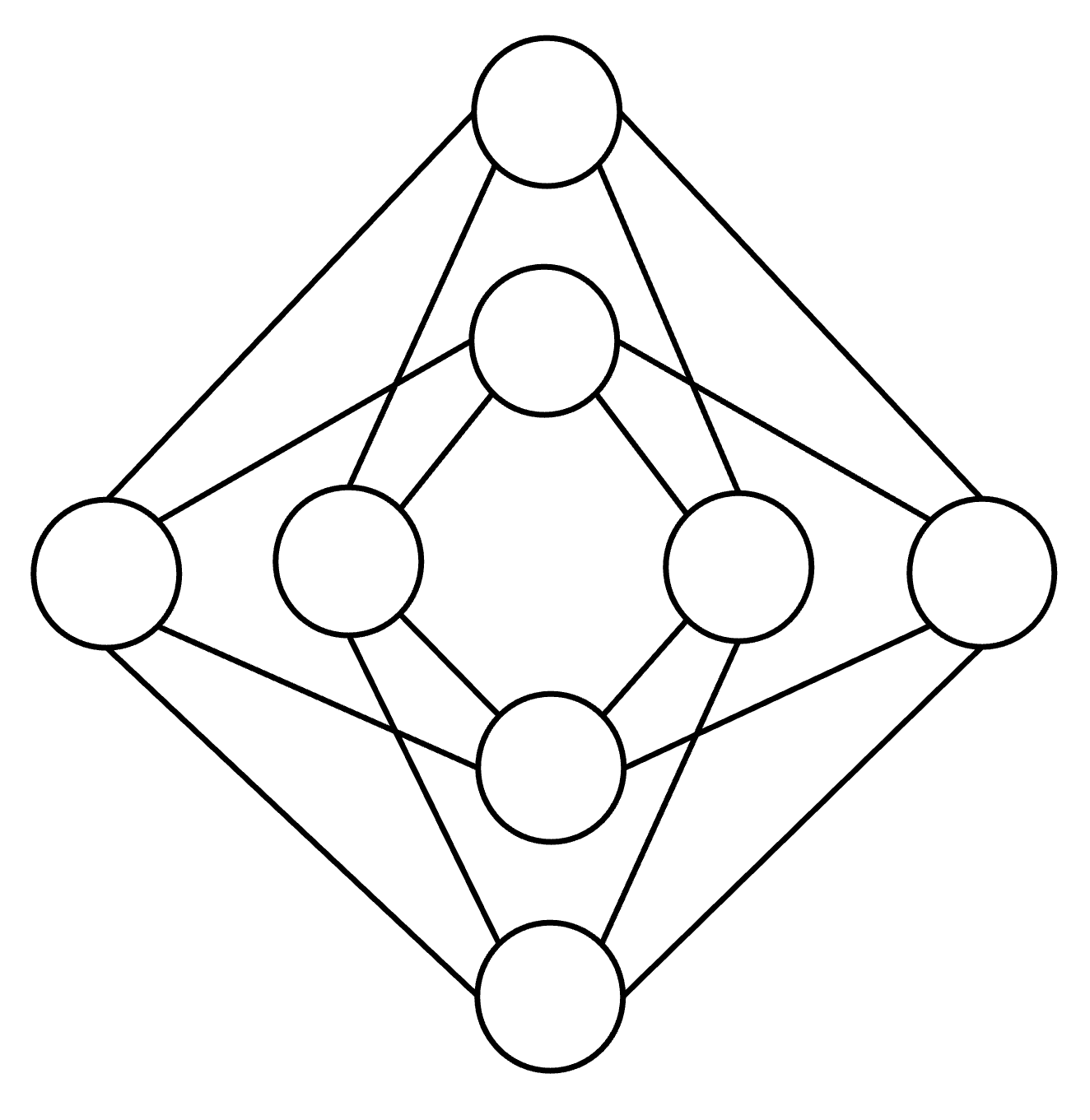
　図1: キメラグラフ

例えば、図2のようなグラフ構造を持つ問題であれば、そのまま解きたい問題をマッピングすることが出来ます。

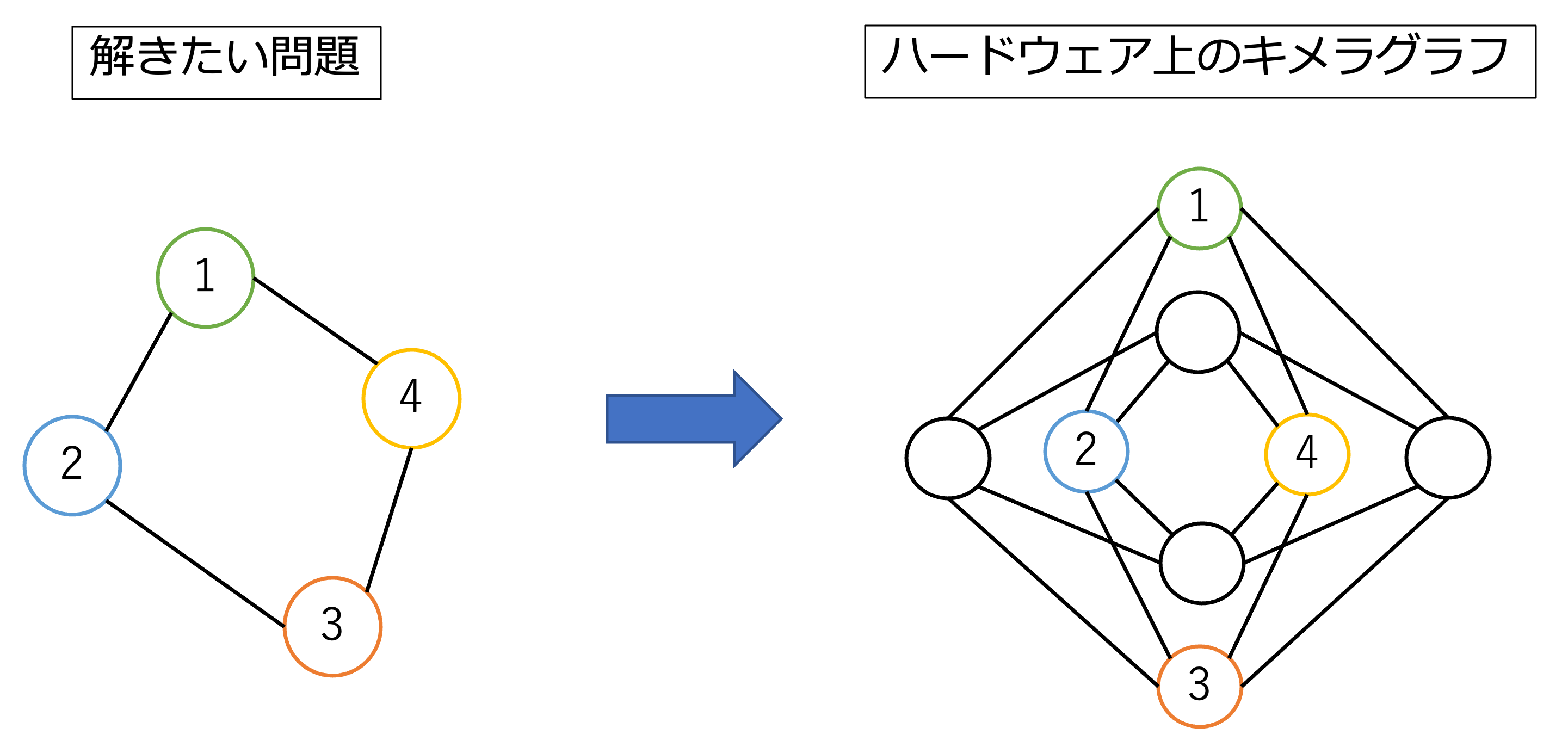
図2: マッピングが容易な例

しかし、図3のようにノード1とノード3の間に結合がある場合、キメラグラフ上に直接マッピングすることが出来ません。そのため、図3の右図のように、複数の量子ビットで1つのノードを表すようなマッピングを行います。これを、マイナー埋め込みと言います。

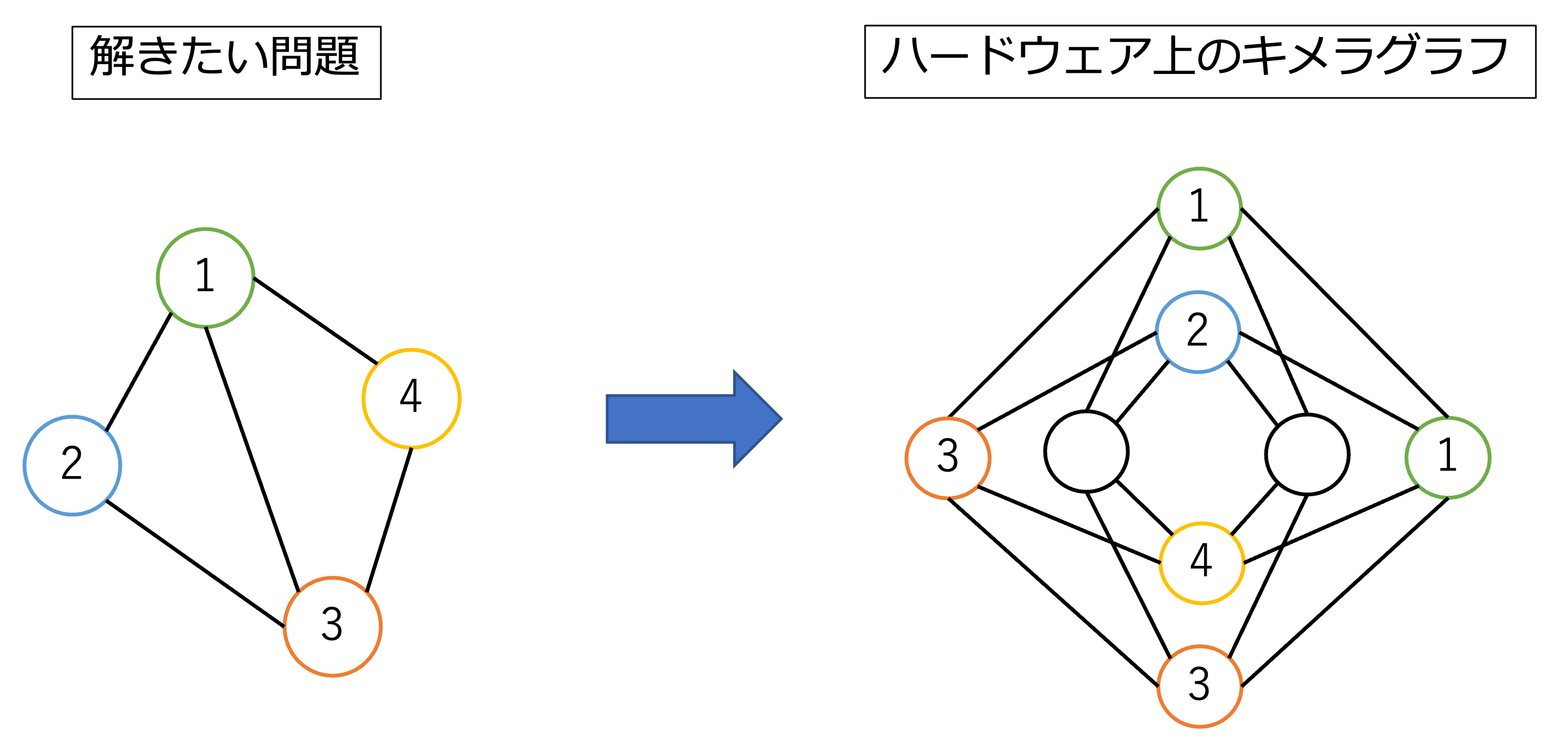
図3: マッピングが複雑な例

図3の場合、解きたい問題のノード数は4個ですが、ハードウェア上では6個の量子ビットが使用されてしまいます。解きたい問題のグラフが密になればなるほど、使用する量子ビットは増加します。このようなハードウェア上の制限により、D-Wave 2000Qは最大2048個の量子ビットが使用可能ですが、実際に解ける問題サイズはかなり小さいものになってしまいます。現在はD-Wave 2000Qのサービスは終了してしまいましたが、最新のD-Wave Advatageでも依然この問題は残っています。 そこで本論文では、使用できる量子ビット数を減らさずに問題を解くことが出来る、新たなアルゴリズムを提案します。

準備

最適化問題を量子アニーリングマシンで解くには、問題をQuadratic Unconstrained Binary Optimization(QUBO)で表す必要があります。このとき、QUBOをコスト項と制約項の和で表すことがよくあります。

$$
\begin{equation}\tag{1}
f(\boldsymbol q) = f_0(\boldsymbol q) + \frac{1}{2}\sum_{k} \lambda_{k} \left( F_{k}(\boldsymbol q) – C_{k}\right)^2
\end{equation}
$$

ここで、$q_i \in \{0, 1\}$、$f_{0}(\boldsymbol q)$がコスト項、$\frac{1}{2}\sum_{i} \lambda_{i} \left( F_{i}(\boldsymbol q) – C_{i}\right)^2$は制約項です。制約項は等式制約を表しています。一般形では分かりにくいので、次のような具体的な問題を考えましょう。

• N個の乱数からK個選び出し、その総和が最小となる組み合わせを探索する問題

この問題の場合、QUBOは次のようになります。

$$
\begin{equation}\tag{2}
f(\boldsymbol q) = \sum_{i=1}^{N}h_iq_i + \frac{\lambda}{2}\left( \sum_{i=1}^{N}q_{i} – K \right)^2
\end{equation}
$$

ここで、$q_{i}$はバイナリ変数で、$h_{i}$は乱数の値、$\lambda$はハイパーパラメータです。
第2項が制約項になっており、問題文の「N個の乱数からK個選び出し」という部分を表しています。数式で書くと、$\sum_{i=1}^{N}q_{i} = K$という等式制約を表しています。ここで、制約項を展開してみましょう。

$$
\begin{equation}\tag{3}
\frac{\lambda}{2}\left( \sum_{i=1}^{N}q_{i} – K \right)^2=\frac{\lambda}{2}\left( \sum_{i=1}^{N}\sum_{j=1}^{N}q_{i}q_{j} -2K\sum_{i=1}^{N}q_{i} + K^2 \right)
\end{equation}
$$

第1項の$\sum_{i=1}^{N}\sum_{j=1}^{N}q_{i}q_{j}$に注目してください。これは、全ての$q_{i}$と全ての$q_{j}$の間に$\frac{\lambda}{2}$の重みがあることを意味しています。つまり、この問題は全結合のグラフで表されるということです。前述したように、結合が多くなるほど無駄に使用する量子ビットが増えてしまいます。

これから紹介する「大関法」では、問題の根源である2次式の制約項を上手く変形することで、量子ビットを無駄なく最大限利用できるようにしていきます。

大関法

まずは、2次式を1次式に変換する公式を紹介します。

ハバード・ストラトノヴィッチ変換

この変換式はガウス積分から導かれます。まずは、ガウス積分を確認しましょう。

• ガウス積分：
  $$
  \begin{equation}\tag{4}
  \int_{-\infty}^{\infty}\exp\left({-ax^2}\right)dx=\sqrt{\frac{\pi}{a}}
  \end{equation}
  $$

ここで、$\exp$の中身を$-\frac{1}{2}ax^2+bx$として式変形すると以下のようになります。

$$
\begin{equation}\tag{5}
\begin{split}
\int_{-\infty}^{\infty}\exp\left({-\frac{1}{2}ax^2+bx}\right)dx
&= \int_{-\infty}^{\infty}\exp\left({-\frac{1}{2}a\left( x- \frac{b}{a} \right)^2+ \frac{b^2}{2a}}\right)dx \\
&= \sqrt{\frac{2\pi}{a}}\exp{\left( \frac{b^2}{2a} \right)}
\end{split}
\end{equation}
$$

1行目では平方完成、2行目ではガウス積分をしています。$b$を変数として逆から読むと、次のように書くことが出来ます。

$$
\begin{equation}\tag{6}
\exp{\left( \frac{b^2}{2a} \right)} = \sqrt{\frac{a}{2\pi}}\int_{-\infty}^{\infty}\exp\left({-\frac{1}{2}ax^2+bx}\right)dx
\end{equation}
$$

$b$の2次式が1次式に変換されていることが分かります。これを、ハバード・ストラトノヴィッチ変換と言います。早速、2次の制約項に適用してみましょうと言いたいところですが、ハバード・ストラトノヴィッチ変換は$\exp$の中身を1次式に変換するものです。制約項をそのまま変換することは出来ません。そこで、$f(\boldsymbol{q})$の分配関数を考えてみます。

• 分配関数：
  $$
  \begin{equation}\tag{7}
  Z \equiv \sum_{\boldsymbol{q}} \exp{\left( -\beta f(\boldsymbol{q})\right)}
  \end{equation}
  $$

この形であれば、ハバード・ストラトノヴィッチ変換が適用できそうです。それでは、変換していきましょう。

$$
\begin{equation}\tag{8}
\begin{split}
Z &= \sum_{\boldsymbol{q}} \exp{\left( -\beta f(\boldsymbol{q})\right)}\\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) – \frac{\beta}{2} \sum_{k} \lambda_{k} \left( F_{k}(\boldsymbol{q}) – C_{k} \right)^2\right)} \\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\prod_{k}\exp{\left( -\frac{\beta}{2}\lambda_{k}\left( F_{k}(\boldsymbol{q}) – C_{k} \right)^2\right)}\\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\prod_{k}\frac{1}{\sqrt{2\pi}}\int\exp{\left( -\frac{1}{2}z_{k}^2 + i\sqrt{\beta\lambda_{k}}\left( F_{k}(\boldsymbol{q}) – C_{k} \right)z_{k} \right)}dz_{k}\\
&= \frac{1}{\sqrt{2\pi}}\sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\prod_{k}\int\exp{\left( -\frac{1}{2}z_{k}^2 + i\sqrt{\beta\lambda_{k}}z_{k}\left( F_{k}(\boldsymbol{q}) – C_{k} \right) \right)}dz_{k}\\
&\propto \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\prod_{k}\int\exp{\left(\frac{\beta}{2\lambda_{k}}\nu_{k}^2 + \beta \nu_{k} \left( F_{k}(\boldsymbol{q}) – C_{k} \right) \right)}d\nu_{k}\\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\prod_{k}\int\exp{\left( g(\nu_{k})\right)d\nu_{k}}
\end{split}
\end{equation}
$$

変形途中ですが、ここで1度区切ります。各行の説明をしましょう。

• 2~3行目

以下の具体例のように、$\exp$の中の総和を$\exp$の外側に総積で書くことが出来ることを利用しました。
$$
\exp{\left( \sum_{k=1}^3  x_{k}\right)}=\exp{\left( x_1 + x_2 + x_3 \right)} = \exp{\left( x_1 \right)}\exp{\left( x_2 \right)}\exp{\left( x_3 \right)}=\prod_{k=1}^3\exp{\left(  x_{k} \right)}
$$

• 3~4行目

ハバード・ストラトノヴィッチ変換を利用しています。具体的には、先程の変換式(1)に$a=1, b=\sqrt{-\beta \lambda_{k} \left( F_{k}(\boldsymbol{q})- C_{k}\right)^2}$を当てはめることで導出できます。

• 5~6行目

$i\sqrt{\beta \lambda_{k}}z_{k} = \beta \nu_{k}$つまり、$z_{k} = -i \sqrt{\frac{\beta}{\lambda_{k}}} \nu_{k}$と変数変換を行っています。

• 6~7行目

$\frac{\beta}{2\lambda_{k}}\nu_{k}^2 + \beta \nu_{k} \left( F_{k}(\boldsymbol{q}) – C_{k}\right)$を$g(\nu_k)$と置いています。

それでは、変形に戻ります。

$$
\begin{equation}\tag{9}
\begin{split}
Z &= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\prod_{k}\int\exp{\left( g(\nu_{k})\right)d\nu_{k}}\\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)}\int\exp{\left( g(\nu_{0})\right)d\nu_{0}}\int\exp{\left( g(\nu_{1})\right)d\nu_{1}} \cdots\\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)} \prod_{k} \int d\nu_k  \exp{\left( \sum_{k} g(\nu_k) \right)}\\
&= \sum_{\boldsymbol{q}} \exp{\left( -\beta f_{0}(\boldsymbol{q}) \right)} \prod_{k} \int d\nu_k  \exp{\left( \sum_{k} \frac{\beta}{2\lambda_{k}}\nu_{k}^2 + \beta \nu_{k} \left( F_{k}(\boldsymbol{q}) – C_{k}\right) \right)}\\
&= \sum_{\boldsymbol{q}} \prod_{k} \int d\nu_k  \exp{\left(-\beta f_{0}(\boldsymbol{q})+ \sum_{k} \frac{\beta}{2\lambda_{k}}\nu_{k}^2 + \beta \nu_{k} \left( F_{k}(\boldsymbol{q}) – C_{k}\right) \right)}\\
&= \sum_{\boldsymbol{q}} \prod_{k} \int d\nu_k  \exp{\left( -\beta H(\boldsymbol{q}, \boldsymbol{\nu}) \right)}
\end{split}
\end{equation}
$$

これにより、有効ハミルトニアンが得られました。

$$
\begin{equation}\tag{10}
H(\boldsymbol{q}, \boldsymbol{\nu})=f_{0}(\boldsymbol{q}) – \sum_{k} \frac{\nu_{k}^2}{2\lambda_{k}} – \nu_{k} \left( F_{k}(\boldsymbol{q}) – C_{k}\right)
\end{equation}
$$

これを最小化するような$(\boldsymbol{q}, \boldsymbol{\nu})$が最終的に求めたい解です。そこで、鞍点法を用いて$H(\boldsymbol{q}, \boldsymbol{\nu})$を最小化しましょう。

鞍点法

$f(t)$が正則で、$\beta \rightarrow \infty$ の時、以下が成り立ちます。

$$
\begin{equation}\tag{11}
\int d t \exp (\beta f(t)) \propto \exp \left(\beta f(t^*)\right)
\end{equation}
$$

ここで、$t^*$は鞍点であり、$f(t^*)$は最大値となります。
これを式(9)に適用すると、次のようになります。

$$
\begin{equation}\tag{12}
Z \propto \exp \left(- \beta H(\boldsymbol{q}^*,\boldsymbol{\nu}^* )\right)
\end{equation}
$$

ここで、$(\boldsymbol{q}^*,\boldsymbol{\nu}^* )$が鞍点であり、$H(\boldsymbol{q^*},\boldsymbol{\nu^*} )$は最小値となります。ここからは、$(\boldsymbol{q}^*,\boldsymbol{\nu}^* )$を求めていきましょう。
まず、鞍点の性質について確認します。
鞍点は図4のように、ある方向から見ると極小であり、ある方向から見ると極大となります。

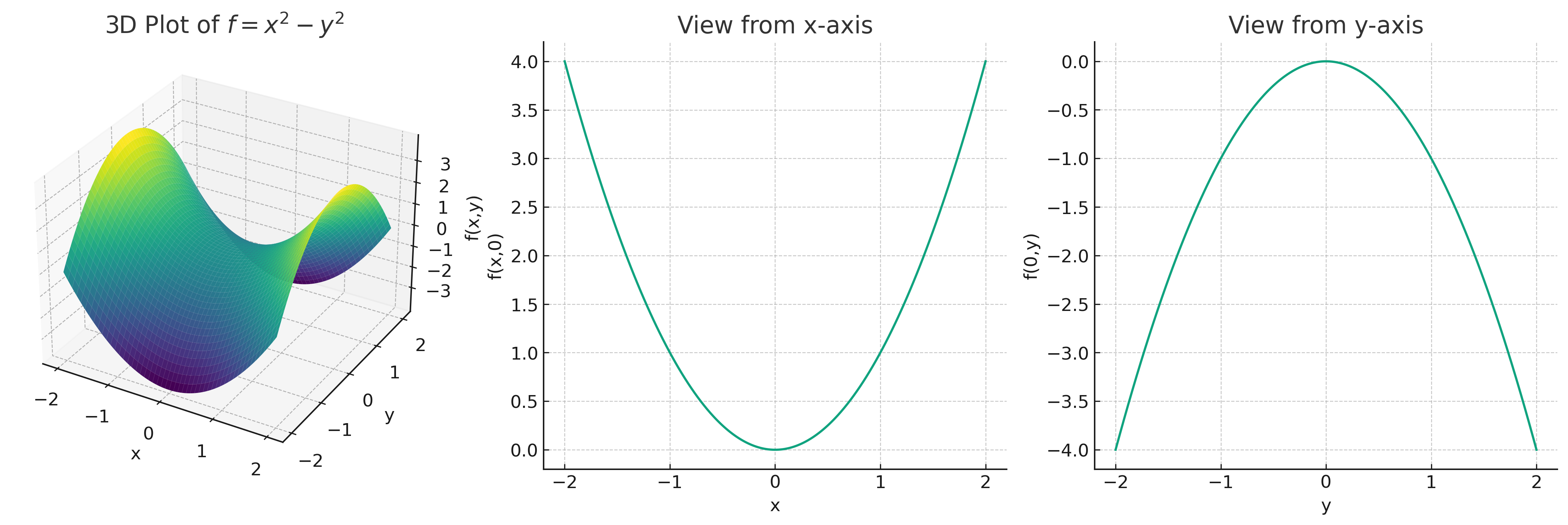
図4: 鞍点の3D図

それでは、$\boldsymbol{q}^*$や$\boldsymbol{\nu}^*$は極大・極小のどちらになるでしょうか。
$H(\boldsymbol{q},\boldsymbol{\nu})$について、$\nu_k$の２次導関数を求めてみましょう。

$$
\begin{equation}\tag{13}
\frac{\partial^2}{\partial \nu_k^{2}} H(\boldsymbol{q},\boldsymbol{\nu}) =-\frac{1}{\lambda_k}
\end{equation}
$$

$\lambda_k$は正のため、$\frac{\partial^2 H}{\partial \nu_k^2}<0$となります。従って、$H(\boldsymbol{q},\boldsymbol{\nu})$は、$\boldsymbol{\nu}$軸方向で極大値をもちます。
また、$i\sqrt{\beta\nu_k}z_{k}=\beta \nu_k$と変数変換したので、$\boldsymbol{\nu}$は虚軸方向です。従って、実軸方向である$\boldsymbol{q}$軸方向から見ると、鞍点は極小となります。

まずは、$\boldsymbol{\nu}$軸方向から見た鞍点を勾配法で求めていきましょう。そのために、$Z$を次のように変形していきます。

$$
\begin{equation}\tag{14}
\begin{aligned}
Z & \propto \sum_{\boldsymbol{q}}\prod_{\boldsymbol{k}} \int d \nu_k \exp (-\beta H(\boldsymbol{q}, \boldsymbol{\nu})) \\
& =\sum_{\boldsymbol{q}}\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta f_0(\boldsymbol{q})+\sum_k\left(\frac{\beta}{2 \lambda_k} \nu_k^2+\beta \nu_k\left(F_k(\boldsymbol{q})-C_k\right)\right)\right) \\
& =\sum_{\boldsymbol{q}}\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta f_0(\boldsymbol{q})+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2+\beta \sum_k \nu_k F_k(\boldsymbol{q})-\beta \sum_k \nu_k C_k\right) \\
& =\sum_{\boldsymbol{q}}\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta \sum_k \nu_k C_k+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2+\beta \sum_k \nu_k F_k(\boldsymbol{q})-\beta f_0(\boldsymbol{q})\right) \\
& =\sum_{\boldsymbol{q}}\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta \sum_k \nu_k C_k+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2\right) \exp \left(\beta \sum_k \nu_k F_k(\boldsymbol{q})-\beta f_0(\boldsymbol{q})\right) \\
& =\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta \sum_k \nu_k C_k+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2\right) \sum_{\boldsymbol{q}} \exp \left(-\beta\left(f_0(\boldsymbol{q})-\sum_k \nu_k F_k(\boldsymbol{q})\right)\right) \\
& =\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta \sum_k \nu_k C_k+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2\right) Z(\boldsymbol{\nu}) \\
& =\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta \sum_k \nu_k C_k+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2\right) \exp (\log (Z(\boldsymbol{\nu}))) \\
& =\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta \sum_k \nu_k C_k+\beta \sum_k \frac{1}{2 \lambda_k} \nu_k^2+\log (Z(\boldsymbol{\nu}))\right) \\
& =\prod_{\boldsymbol{k}} \int d \nu_k \exp \left(-\beta\left(\sum_k \nu_k C_k-\sum_k \frac{1}{2 \lambda_k} \nu_k^2-\frac{1}{\beta} \log (Z(\boldsymbol{\nu}))\right)\right) \\
& =\prod_{\boldsymbol{k}} \int d \nu_k \exp (-\beta(H(\boldsymbol{\nu})))
\end{aligned}
\end{equation}
$$

これにより、$H(\boldsymbol{\nu})$が得られました。

$$
\begin{equation}\tag{15}
H(\boldsymbol{\nu})=\sum_k \nu_k C_k-\sum_k \frac{1}{2 \lambda_k} \nu_k^2-\frac{1}{\beta} \log (Z(\boldsymbol{\nu}))
\end{equation}
$$

ここで、$Z(\boldsymbol{\nu}) := \sum_{\boldsymbol{q}} \exp \left(-\beta\left(f_0(\boldsymbol{q})-\sum_k \nu_k F_k(\boldsymbol{q})\right)\right)$と置いています。$\lambda_{k}$は罰金項の係数なので、非常に大きな値を持ちます。そこで、$\lambda_{k} \to \infty$としても問題ありません。従って、次のハミルトニアンが得られます。

$$
\begin{equation}\tag{16}
H(\boldsymbol{\nu})=\sum_k \nu_k C_k – \frac{1}{\beta} \log (Z(\boldsymbol{\nu}))
\end{equation}
$$

これを$\nu_{k}$で偏微分しましょう。

$$
\begin{equation}\tag{17}
\begin{aligned}
\frac{\partial}{\partial \nu_k} H(\boldsymbol{\nu}) & =C_k-\frac{1}{\beta} \frac{\partial}{\partial \nu_k} \log (Z(\boldsymbol{\nu})) \\
& =C_k-\frac{1}{\beta} \frac{1}{Z(\boldsymbol{\nu})} \frac{\partial Z(\boldsymbol{\nu})}{\partial \nu_k} \\
& =C_k-\frac{1}{\beta} \frac{\sum_{\boldsymbol{q}} \beta F_k(\boldsymbol{q}) \exp \left(-\beta\left(f_0(\boldsymbol{q})-\sum_k \nu_k F_k(\boldsymbol{q})\right)\right)}{\sum_{\boldsymbol{q}} \exp \left(-\beta\left(f_0(\boldsymbol{q})-\sum_k \nu_k F_k(\boldsymbol{q})\right)\right)} \\
& =C_k- \sum_{\boldsymbol{q}} F_k(\boldsymbol{q})\frac{\exp \left(-\beta\left(f_0(\boldsymbol{q})-\sum_k \nu_k F_k(\boldsymbol{q})\right)\right)}{\sum_{\boldsymbol{q}} \exp \left(-\beta\left(f_0(\boldsymbol{q})-\sum_k \nu_k F_k(\boldsymbol{q})\right)\right)} \\
& =C_k- \sum_{\boldsymbol{q}} F_k(\boldsymbol{q})P(\boldsymbol{q}) \\
& =C_k- \left \langle F_k(\boldsymbol{q})\right\rangle_q
\end{aligned}
\end{equation}
$$

従って、勾配法は以下を計算します。

$$
\begin{equation}\tag{18}
\nu_k^{t+1}=\nu_k^t+\eta\left(C_k-\left\langle F_k(\boldsymbol{q})\right\rangle_q\right)
\end{equation}
$$

ここで、$\left\langle F_k(\boldsymbol{q})\right\rangle_q=\sum_{\boldsymbol{q}} F_k(\boldsymbol{q})P(\boldsymbol{q})$は$F_k(\boldsymbol{q})$の期待値であり、厳密に計算するのは大変です。そこで、D-Waveマシンからの出力がギブス・ボルツマン分布に従うという特徴を利用して、以下の手続きで近似計算を行いましょう。まず、何らかの$\boldsymbol{\nu}$で固定した$H(\boldsymbol{q}, \boldsymbol{\nu})$に対して、D-Waveマシンから$\boldsymbol{q}$をサンプリングします。これらのサンプルはボルツマン分布$P(\boldsymbol{q})$に従うので、
$$
P(\boldsymbol{q}) := \boldsymbol{q}の出現回数 / サンプリング回数
$$
として計算出来ます。このようにして、期待値の近似計算が可能になります。

まとめると、大関法の手順は以下のようになります。

• Step1: 元のハミルトニアンを変換する
  $$
  f(\boldsymbol{q})=f_0(\boldsymbol{q})+\frac{1}{2} \sum_i \lambda_i\left(F_i(\boldsymbol{q})-C_i\right)^2 \quad\to\quad
  H(\boldsymbol{q}, \boldsymbol{\nu})=f_0(\boldsymbol{q})-\sum_i \nu_i\left(F_i(\boldsymbol{q})-C_i\right) \\
  $$
• Step2: $\boldsymbol{\nu}$を初期化する
• Step3: $\boldsymbol{\nu}$を固定して、D-Waveマシンで$\boldsymbol{q}$をサンプリングする
• Step4: $\left\langle F_k(\boldsymbol{q})\right\rangle_q$を計算して、勾配法で$\boldsymbol{\nu}$を更新する
• Step5: $\boldsymbol{\nu}$が収束するまで、Step3,4を繰り返す

次のセクションでは、実験結果を紹介します。論文では6つの最適化問題に取り組んでいますが、本記事では2つのみ取り上げます。

実験

「N個の乱数からK個選び、その和を最小にする問題」を解いていきます。この問題のコスト関数と変換後のコスト関数は次のようになります。

$$\tag{19}
f(\boldsymbol{q})=\sum_{i=1}^N h_i q_i+\frac{\lambda}{2}\left(\sum_{i=1}^N q_i-K\right)^2 \quad\to\quad H(\boldsymbol{q}, \nu)=\sum_{i=1}^N h_i q_i-\nu\left(\sum_{i=1}^N q_i-K\right)
$$

ここで、$N=2000, K=5, \nu^{t=0}=0$としています。結果は図5のようになります。

図5: 実験結果,[引用]https://www.nature.com/articles/s41598-020-60022-5

左図は、step毎の残差エネルギーを示しています。右図は、step毎の$\nu$の値を示しています。3step目で、$\nu$が収束し最適解を見つけられていることが分かります。

次に、「数分割問題」を解いていきます。この問題は、コスト項が2次となる問題です。コスト関数と変換後のコスト関数は次のようになります。

$$\tag{20}
f(\boldsymbol{q})=\frac{1}{2}\left(\sum_{i=1}^N n_{i}q_{i}\right)^2 \quad\to\quad H(\boldsymbol{q}, \nu)=\nu\sum_{i=1}^N n_{i}q_{i}
$$

ここで、$N=2000$と設定しています。結果は図6のようになります。

図6: 数分割問題の結果,[引用]https://www.nature.com/articles/s41598-020-60022-5

結果の見方は、図5と同様です。こちらに関しても、約12stepで最適解を見つけられています。

これらの問題サイズの場合、通常はD-Wave 2000Qで解くことは出来ません。一方で、大関法は、$\boldsymbol{\nu}$も探索しなければいけなくなるものの、扱える問題サイズが飛躍的に向上します。使用できる量子ビット数が限られている現状において、このような手法は非常に重要な意味を持つといえるでしょう。

あとがき

実験結果を見ると、$\boldsymbol{\nu}$は振動することなく収束しています。しかし、勾配法の学習率$\eta$の値を適切に設定しないと、上手く収束しないという結果もあります[1]。これは、$\boldsymbol{q}$と$\boldsymbol{\nu}$の学習速度の違いが関係しているのではないかと考えました。 つまり、$\boldsymbol{q}$に関しては1stepで鞍点に到達するものの、$\boldsymbol{\nu}$に関しては勾配法でゆっくりと鞍点を目指しています。これにより、$\eta$の値によっては$\boldsymbol{\nu}$が振動してしまう場合があると考えられます。

参考文献

[1] https://github-nakasho.github.io/mo/ohzeki

本記事の担当者

鹿内怜央