文献情報
- タイトル: Job Shop Scheduling Solver based on Quantum Annealing
- 著者: Davide Venturelli, Dominic J.J. Marchand, Galo Rojo
- arXiv:1506.08479 [quant-ph]
概要
組合せ最適化問題の一つであるジョブショップスケジューリング問題を定式化し、これをD-Wave Twoにより解いた。
問題
ジョブショップスケジューリング問題(JSP:Job Shop Scheduling Problem)とは、機械を用いて複数のジョブを処理する場合に、全体の稼働時間やコストを最小にする問題である。各ジョブには複数のオペレーションが含まれ、各オペレーションには実行する機械に対して所要時間が決まっている。
今回は以下の制約のもとで、オペレーションを機械に割り当てて、全てのジョブが完了するまでにかかる時間を最小化する。
- あるジョブのオペレーション開始時刻には、順序が与えられる
- 機械は一度に、1つのオペレーションしか処理できない
- オペレーションを開始したら、途中では中断できない
最適化問題の定式化
組合せ最適化問題の種類: ジョブショップ・スケジューリング問題
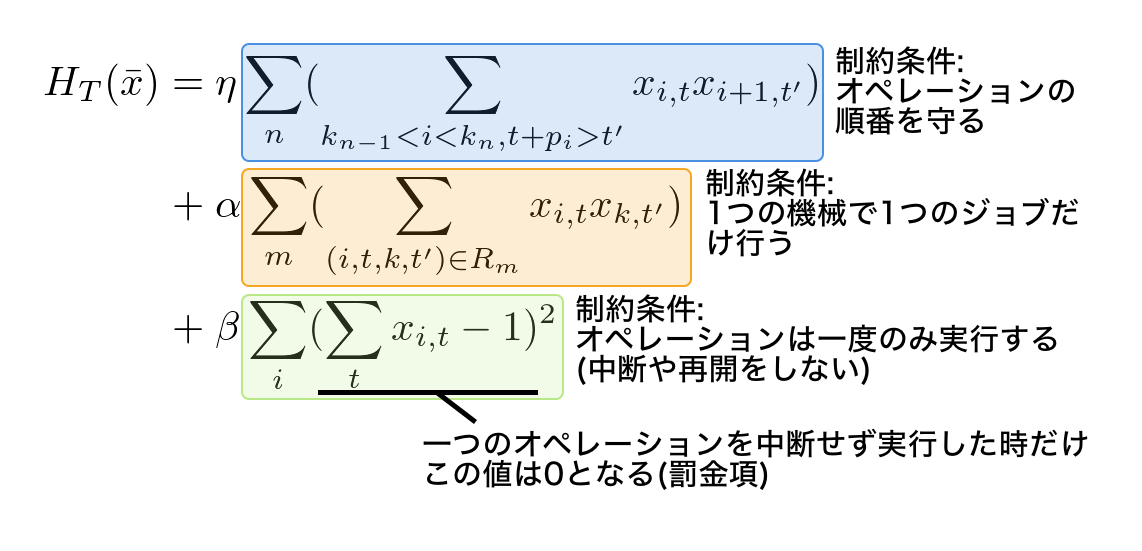
変数: $x_{i,t} \in \{0,1\}$ (オペレーション$O_i$が時刻$t$に始まるとき$1$, そうでなければ$0$)
目的関数:
ただし、$\eta, \alpha, \beta > 0$
- ジョブのオペレーションの順番を守ること:
- 1つの機械で1つのジョブだけ行なうこと:
- 1つのオペレーションを開始したら、中断や再開をしないこと:
各オペレーションと実行する機械に対する所要時間の例を示す。なお、$m$は機械、$j$はジョブ、$O$はオペレーションを表している。
上記の例をQUBOへマッピングした図を示す。$t$は単位時間を表している。
色付きのブロックはオペレーションの開始時間の候補であり、色付きのブロックを結ぶ点線はオペレーションの順番を守るという制約条件である。上記の例から、所要時間が2であるオペレーション$O_1$を$t_2$に開始する場合、$O_2$を$t_3$に開始すると順番を守ってないことになる。
D-Waveマシン実装上の工夫
変数選定: オペレーションの順番に従っていない変数を選定する。
所要時間の推定: 古典的なソルバーを用いて解を計算することで、サイズ$N = M$によってパラメータ化された変数の異なるアンサンブルに対する、最適な所要時間の分布が得られる。この分布から、最適化問題を解決するために必要な二分探索を得るために使用できる。
パラメータ設定: 「オフライン」パラメータ設定
結果
D-wave Twoを用いて、$H_{\cal T}$の基底状態で成功確率が99%に達するまでにかかるアニーリングの試行回数(アニーリング時間は20[$\mu s$])は、問題サイズの増加に伴って指数関数的に増加した。
また、D-Waveの実行時間と、完全な解が出せる二つの古典的アルゴリズム(分枝限定法、MSアルゴリズム)の実行時間を比較した。分枝限定法の結果は、D-Waveの結果を上回った。一方、MSアルゴリズムによって解くのに約$10^{-3}$秒かかる問題に対して、D-Waveではその半数を約$10^{-4}$〜$10^{-5}$秒で解いた。
今回の問題サイズは小さすぎるため、より多くの量子ビットによって、より大きな問題サイズに対する漸近的挙動を実証し測定する必要がある。
本記事の担当者
丸山尚貴