概要
先日開催された量子アニーリングソリューションコンテストにTQARD-410として参加し、量子アニーリングでフォトモザイクアートを作成するPhosaiqを提案しました。Phosaiqは画像の並びを最適化したフォトモザイクアートを作成し、またユーザーが調整することでフォトモザイクアートの質とユーザの体験価値を高めるプロダクトです。このコンテストにおいて、Phosaiqは優勝(D-Wave Systems社賞を受賞)することができました。
ここではPhosaiqの説明をするとともに、動画やスライドでは省略した類似度の求め方について説明します。
フォトモザイクアート
フォトモザイクアートは多数の写真を並べて1つの大きなイメージを構成する表現方法です。近くで見ると画像の羅列にしか見えませんが、全体として見るとそれが一つの絵であることがわかるというのが特徴です。

フォトモザイクアートを人手で作成しようとすると時間と手間を要し、またプロに頼むとしても費用が高く個人のデータを渡したくないという欠点もあります。そこで単純なアルゴリズムなど自動化しようとすると、類似度が高い画像を1枚ずつ割り当てる方法があります。しかしこれでは同じ画像が何枚も使われ、またすべてのユースケースに対し作成方法が画一的になります。
ソリューション
定式化
私たちが提案するソリューションPhosaiqでは、これらの問題を組み合わせ最適化問題として捉えることで解決を試みます。
まず定式化について説明します。入力として画像[latex]\mu[/latex]と区画[latex]i[/latex]の類似度を表す[latex]S_{\mu i}[/latex]を用意します。これは0から1の間で表され、小さいほど似ていることを表します(後述)。次に決定変数として[latex]x_{\mu i}[/latex]を用います。これは画像[latex]\mu[/latex]が区画[latex]i[/latex]に割り当てられるとき1、そうでないときに0となる2値変数です。定式化は以下の通りとなります。
\begin{equation}
H = \sum_{\mu=1}^{M} \sum_{i=1}^{N} S_{\mu i} x_{\mu i} + \lambda_{1} \sum_{i=1}^{N}\left(\sum_{\mu=1}^{M} x_{\mu i}-1\right)^{2} + \lambda_{2} \sum_{\mu=1}^{M} \sum_{i, j \in E} x_{\mu i} x_{\mu j}
\end{equation}
第1項は類似度が高い画像を割り当てることを表します。第2項は1つの区画に割り当てる画像は1枚だけとする制約項です。第3項は隣り合った区画に割り当てる画像は異なるものにする制約項です。
類似度
動画で省略した類似度について説明します。類似度はLab色空間に基づいて求めます。
[latex]L^{\star}[/latex]が明度、[latex]a^{\star}[/latex]が緑~赤の色、[latex]b^{\star}[/latex]が青~黄の色を表しています。類似度の求め方はいくつかあり、例えば
- 1枚の画像・区画に対してLabの平均値をとり、その平均値のユークリッド距離を類似度とする
- 画素ごとにLabのユークリッド距離をとり、その合計を類似度とする
などがあります。
変数削減
上記の定式化において決定変数[latex]x_{\mu i}[/latex]の個数は[latex]M \times N[/latex]であり、作品の解像度が小さくなったり、素材画像が少なくなってしまいます。そこで、類似度をもとに変数、つまり素材画像の再現画像の区画への割り当てパターンを削減します。
フォトモザイクアートとしての質の向上
今回はオリンピックの画像を用いて聖火の画像を再現してみました。


類似度のみの結果と隣り合う画像についての制約項を入れた場合の結果を比較すると、制約項を入れたときは同じ画像が隣り合う回数が減少していることがわかります。特に青空の部分については同じ画像が隣り合うことがなくなりました。制約項を入れたことでモザイクアートとしての良さが向上したことがわかりました。
様々なユースケースへの対応
組み合わせ最適化問題としてフォトモザイクアートを定式化することで、様々なユースケースに即した作品を制作することができます。追加する制約条件によっては複雑な最適化問題になる場合があり、問題のサイズも考慮すると量子アニーリングマシンが有効な手段の一つであると言えます。
複数人が参加するイベントの場合
文化祭などの複数人が参加するイベントにおいて、記念にフォトモザイクアートを作成する場合があります。その際の問題として、特定の人が作品に多く写ったり逆にほとんど写らなかったりと、出現回数の偏りが生じてしまいます。そこで、それぞれの人物の出現回数の偏りを抑えるために、上記のコスト関数に以下の項を加えます。
\begin{equation}
+\lambda_{3} \sum_{p=1}^{P}\left(\sum_{\mu=1}^{M} \sum_{i=1}^{N} Z_{\mu p} x_{\mu i}-m\right)^{2}
\end{equation}
ただし、[latex]m[/latex]は出現回数の平均値であり、以下のように表されます。
\begin{equation}
m=\frac{1}{P} \sum_{p=1}^{P} \sum_{\mu=1}^{M} \sum_{i=1}^{N} Z_{\mu p} x_{\mu i}
\end{equation}
この項は出現回数の分散を表しており、コスト関数を最小化することで分散が小さくなることが期待できます。このように、分散を直接表現できる点がQUBOの強みの一つであると考えています。
また、[latex]Z_{\mu p}[/latex]は画像[latex]\mu[/latex]に人物[latex]p[/latex]([latex]P[/latex]は対象となる人物の総数)が写っている場合に1、そうでない場合に0をとる定数です。この定数を用意するために、機械学習を用いています。
- 顔検出(Haar Cascades)
- 特徴量抽出(FaceNet)
- 次元削減(PCA)
- クラスタリング(X-Means)
人物の出現回数についての検証として、生田絵梨花さんのプロフィール画像を再現することを考えます。素材となる画像には、乃木坂46のメンバーが複数人写っている画像を695枚使用します。出現回数を均一化しない場合と均一化する場合の類似度は134.0, 129.8であり(小さいほど似ている)、均一化のための項を追加しても作品全体の質はほとんど変わりませんでした。
また、各メンバーの出現回数を比較すると、均一化する場合の方が分散が小さくなっていることが確認できました。
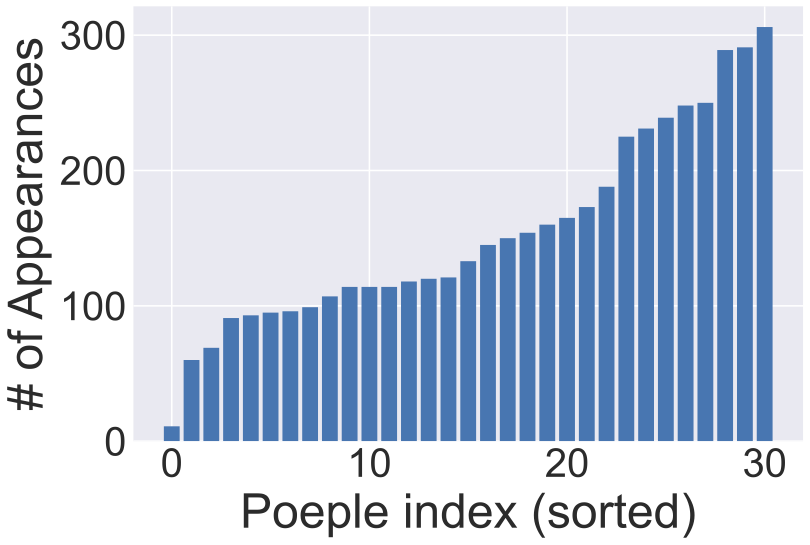
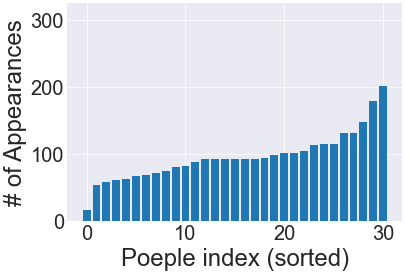
作品における出現回数の偏りを抑えることで、イベントに参加した人にとって、より満足のいく作品を作ることができました。似たようなケースとして例えば、学校の卒業アルバムを作成する際に、各生徒が写る回数をなるべく均等にしたい場合があり、今回新たに追加した項が有効であると考えられます。
画像の順序を考慮する場合
フォトモザイクアートは、動画と組み合わせてより印象的な作品に仕立ていることが可能です。例えば、結婚式では新郎新婦の思い出をフォトモザイクアートと動画によって振り返るという使い方があります。その際に、フォトモザイクアート作品の一部が時系列順になっていれば、自然に二人の思い出を振り返ることができます。画像の順序を考慮するために、コスト関数に以下の項を加えます。
\begin{equation}
+\lambda_{4} \sum_{\mu \nu} \sum_{i, j \in E} A_{\mu \nu}^{i j} x_{\mu i} x_{\nu j}
\end{equation}
[latex]A_{\mu \nu}^{i j}[/latex]は画像[latex]\mu, \nu[/latex]をそれぞれ区画[latex]i,j[/latex]に配置する場合のペナルティを表しています。時系列順に並べる場合は時系列順の場合に0、そうでない場合に1を設定します。
この項の効果を検証するために、以下の画像を再現します。QASCは量子アニーリングソリューションコンテストの略であり、授賞式での発表のためにこの作品を制作しました。

素材としてコンテストに応募した各グループの応募動画から、スライド資料を使用させていただきました。完成した作品は以下のとおりです。

今回の再現画像のように背景が単調の場合、上記の定式化でも同じ画像が繰り返し使用されてしまいます。そこで背景の区画については、コスト関数の計算時に類似度をゼロにすることで、上の完成画像のように単調さを軽減しています。また、変数削減においても、背景の区画では類似度の低い画像も一定の確率で候補に加えることで、モザイクアートとしての乱雑さを残しています。
時系列順に並んでいる箇所を青色で示しています。すべての画像を時系列順に並べることは難しいため、画像の順序はソフトな制約として扱っています。

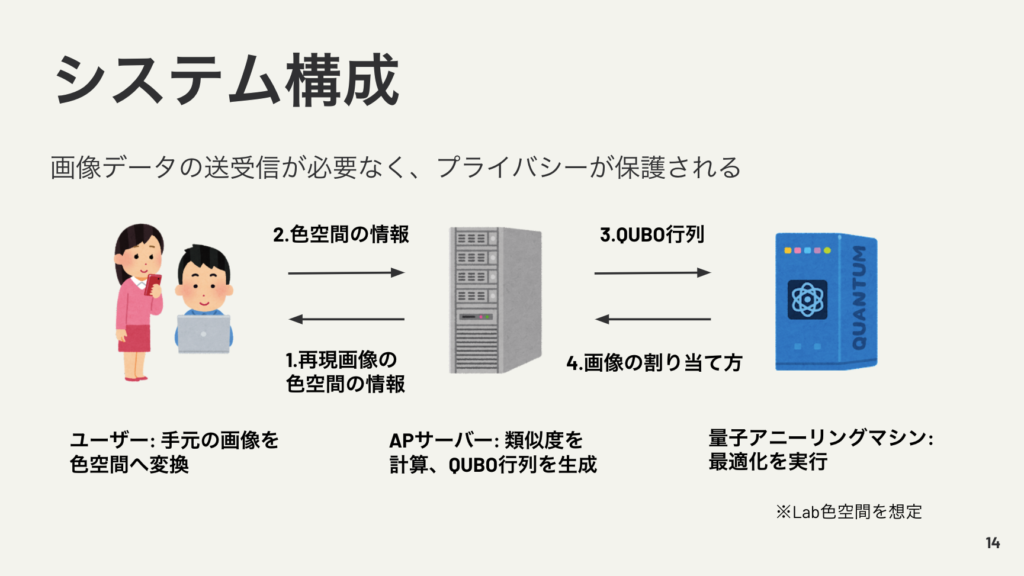
データプライバシーを考慮したシステム構成
定式化を見れば分かる通り、コスト関数は画像のピクセル値でなく類似度のみ与えるため、このアプリケーションでは画像データを送受信する必要がなく、ユーザーのプライバシーが保護されるという利点があります。
まとめ
定式化や実装の工夫、授賞式に向けて新たに行った検証結果など、ソリューションコンテストの応募動画では説明しきれなかった内容を含めて解説しました。今回提案したソリューションをきっかけに量子アニーリングマシンの新たな使い方が生まれることを願いつつ、私たちもT-Waveの活動を通して貢献していきたいと思っています。
本記事の担当者
原知正、丸山尚貴