モンテカルロ法(Monte Carlo Method)とは
モンテカルロ法は確率的な手法を用いて、解析的に困難な数値計算を近似的に行う方法です。ランダムサンプリングを用いて、複雑な数学的問題や高次元の積分、最適化問題などを解くことができます。また、物理学や統計学、金融工学など、様々な分野で広く利用されています。モンテカルロ法の精度はサンプリングの回数(ステップ数)に依存し、一般にステップ数が増えるほど精度が高まります。
具体例として、モンテカルロ法を用いて円周率を求める問題を考えてみます。
以下にその手順を説明します。
- 一辺の長さが1の正方形を考えます。この正方形の内部に、正方形の頂点を中心とした半径1の円の4分の1(扇形)を描きます。
- 次に、正方形の内部にランダムに点を打ちます。この点は一様分布に従ってランダムに配置されます。
- それぞれの点が円の内部にあるか外部にあるかを判定します。
- 扇形の内部にある点の数を全体の点の数で割ります。この比率を4倍すると、円周率の近似値を得ることができます。

この図では、一辺の長さが1の正方形内にランダムに1000個の点を打っています(灰色の点)。その中で、半径1の四分円内に入った点を赤色で表示しています。
この図を見れば、モンテカルロ法の精度がサンプリングの回数(ステップ数)に依存することが直感的にも理解できると思います。
実際に円周率を推定してみる
次に先ほど述べた方法に従って、実際にPythonで円周率を推定してみます。
以下がモンテカルロ法で円周率を推定するためのコードです。
import random
import numpy as np
import matplotlib.pyplot as plt
# モンテカルロ法で円周率を求める関数
def estimate_pi(num_points):
points_inside_circle = 0
for _ in range(num_points):
x = random.uniform(0, 1)
y = random.uniform(0, 1)
distance = x**2 + y**2
if distance <= 1:
points_inside_circle += 1
return 4 * points_inside_circle / num_points
# ステップ数と精度の関係をプロットする関数
def plot_accuracy1():
steps = [10, 100, 1000, 10000, 100000, 1000000]
estimates = [estimate_pi(step) for step in steps]
plt.plot(steps, estimates)
plt.xscale("log")
plt.axhline(y=3.14159, color="r", linestyle="--") # 真の円周率
plt.xlabel("ステップ数")
plt.ylabel("推定値(赤の破線:円周率)")
plt.title("推定値のステップ数による変化")
plt.show()
def plot_accuracy2():
steps = range(10000, 1010000, 10000)
estimates = [estimate_pi(step) for step in steps]
plt.plot(steps, estimates)
plt.axhline(y=3.141592, color="r", linestyle="--") # 真の円周率
plt.xlabel("ステップ数")
plt.ylabel("推定値(赤の破線:円周率)")
plt.title("推定値のステップ数による変化")
plt.show()
import japanize_matplotlib
plot_accuracy1()
plot_accuracy2()
# ステップ数と誤差の関係をプロットする関数
def plot_error():
steps = [10, 100, 1000, 10000, 100000, 1000000]
true_pi = np.pi
errors = [abs(estimate_pi(step) - true_pi) for step in steps]
plt.plot(steps, errors)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("ステップ数")
plt.ylabel("誤差の絶対値")
plt.title("円周率と推定値の誤差のステップ数による変化")
plt.show()
plot_error()
関数estimate_piでモンテカルロ法による推定を行い、関数plot_accuracyで推定結果をプロットしています。
実行してみましょう。
実行すると以下の様なグラフが出力されます。モンテカルロ法による推定なので、実行毎に結果が異なります。
グラフを見る際にはグラフの横軸が対数目盛りであることに留意して下さい。
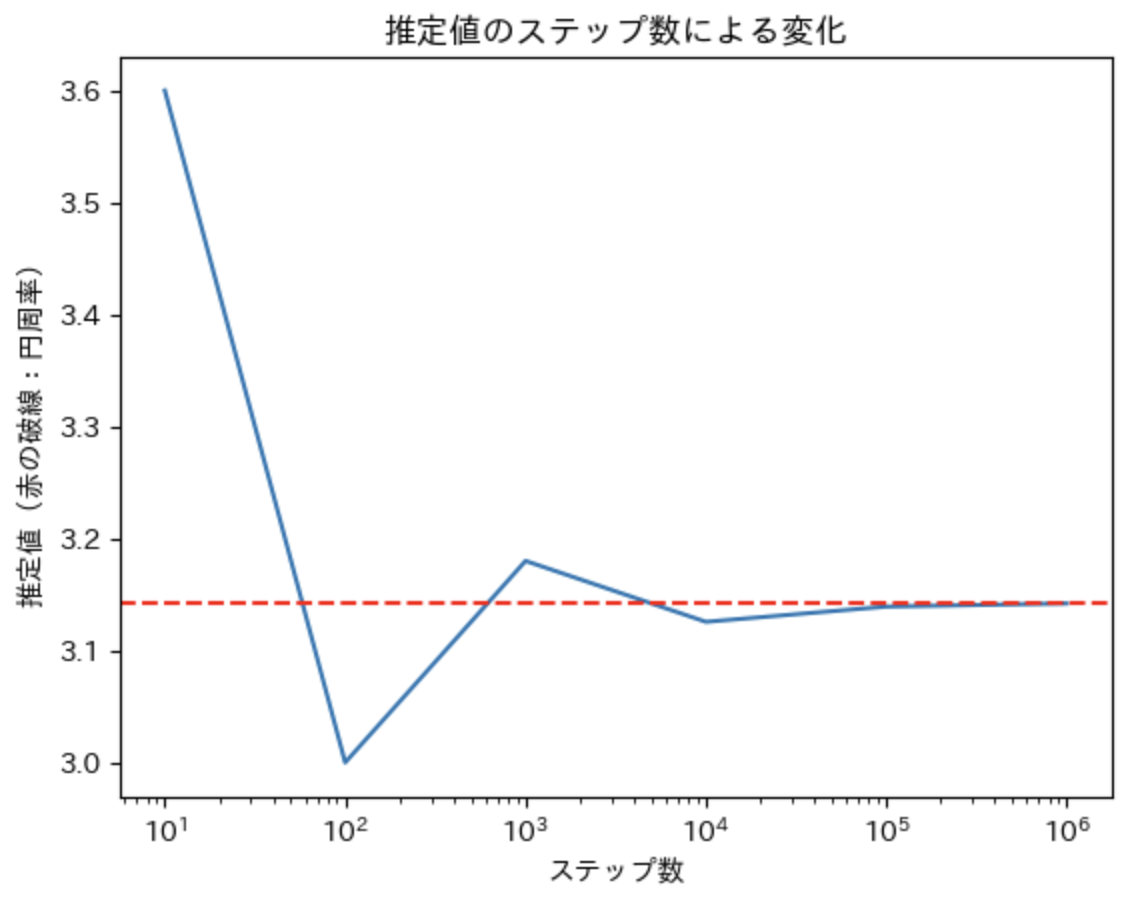
ステップ数が増えるごとに推定値が円周率に近づいていることが見て取れます。