本記事では、Karpの21のNP完全問題の一つである 充足可能性問題 (SAT; satisfiability problem)に関して、最大独立集合問題 (MIS; maximum independent set)に帰着して、問題をQUBO表現に変換する方法を紹介する。本記事作成にあたっては、「組合せ最適化問題のイジングモデル表現 “Ising formulations of many NP problems” by Andrew Lucas (2014)」で紹介した論文を参考にした。
充足可能性問題 とは
充足可能性問題 (SAT)とは、真偽値をとるいくつかの変数によって与えられた命題論理式に対して、変数の値をうまく組み合わせることでその値を真(True)にできるかどうかを判定する問題である。例えば次の例では$x_1 = \text{True},x_2= \text{True}$とすることで論理式はTrueとなる。
$$ {\psi = (x_1 \lor x_4 \lor \overline{x_3} \lor x_6)\land(x_5 \lor x_2)\land(\overline{x_1} \lor x_3 \lor x_2)} $$
ここでは以下のような用語を用いる。
- 論理式$\psi$を構成する変数$x$とその否定$\overline{x}$をまとめてリテラルという。
- 括弧内部のように、リテラルの論理和のみで構成される部分を節という。
- 論理式が節の論理積で構成される場合をCNF-SATという。どんな形の論理式もド・モルガンの法則や分配法則などを用いることで、必ずこの形に帰着できる。
- CNF-SATのうち、特にどの節を構成するリテラル数もたがだかk個となっているものを$k$-SATという。
$k \geq 3$なる$k$-SATはNP完全問題であることが知られており、これを多項式時間で解くアルゴリズムは知られていない。SATは初めてNP完全であることが証明された (Cook-Levinの定理; Cook (1971)) 歴史的にも重要な問題であり、現在でもシステム検証、制約充足問題 (CSP)、スケジューリング、セキュリティなど多様な問題を解くための共通言語としての意味がある。現在広く用いられているSATソルバーはDPDLやCDCLといったアルゴリズムをベースとしており、数百万もの変数を扱うことができるツールとして発展を遂げている。
一方、イジング・QUBO表現を用いたメタヒューリスティック解法としては論理積を強磁性相互作用、論理和を強磁性相互作用と局所磁場で自然に表現したものが考えられるが、3-SATでは3体相互作用を扱う必要がある。D-Waveマシンでは2体の相互作用までしかネイティブに扱うことができないため、1つの補助量子ビットを加えて3体を2体の組み合わせで表現することが主に用いられる。
→ 参考記事(外部サイト)「イジング模型への変換(株式会社フィックスターズ)」
本記事では別解法として、2体の相互作用だけでハミルトニアンが記述可能な最大独立集合問題に帰着することで3-SAT問題を解く方法について解説する。
最大独立集合 (MIS)とは
まず独立集合(independent set)について説明する。独立集合$V’$とは、あるグラフ$G(V,E)$($V$は頂点、$E$は辺の集合)が与えられた時に、頂点のなかで互いに辺を共有していないようなものを要素にもつ、Vの部分集合である。ここで、グラフ$G$において最も大きな独立集合をMISといい、その大きさを$\alpha(G)(= \max |V’|)$で表す。
例えば次のグラフでは、色のついた頂点の集合がMISであることが分かる。

SATのMISへの変換を用いたQUBO表現
大きな流れとしては、
SATの論理式を対応するグラフに変換 → 変換したグラフのMIS問題をQUBO表現に定式化
のようになる。またQUBOを作成する上で、MIS問題が最小被覆問題や、補グラフに対する最大クリーク問題と等価であることに注目して定式化する。
3-SATのグラフへの変換例
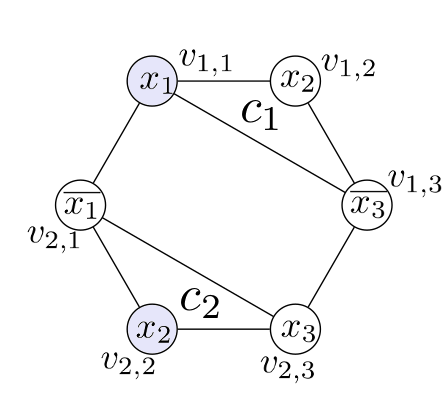
ここでは節数2で、狭義の3-SAT(どの節もリテラル数がちょうど3個)での場合を考える。まず論理式$\psi =(x_1 \lor x_2 \lor \overline{x_3})\land(\overline{x_1} \lor x_3 \lor x_2)$が与えられたとして、対応するグラフ$G(V,E)$を以下の手順に従って作成していく。
- 論理式右辺の節を、左から節$c_1,c_2(c \in C)$とする。
- 節$c_i$中の3変数を、左から頂点$v_{i,1},v_{i,2},v_{i,3}(v \in V)$に対応づけて、頂点を書く。
- 各節と対応する頂点の部分集合について、要素の頂点同士を辺で結ぶ。(このとき図の三角形を形成する)
- ある変数$x$とその否定$\overline{x}$に対応する頂点同士を辺で結ぶ。(三角形同士の連結に相当)
グラフのMISを求めることはSATを解くことと等価
以上のように作ったグラフのMISに関して、次の驚くべき事実が知られている。それは、
グラフのMISの要素数が元のSATの節数と等しい時、SATの論理式はTrueとなる
つまり、式で表せば、
$$ {\alpha(G) = |C| \Leftrightarrow \psi = True} $$
となる。なぜこのようになるかを説明する。
$\alpha(G)=|C| \Rightarrow \psi = \text{True} $ の説明

例えば$v_{1,2}$と$v_{2,1}$を独立集合に含めるとすると、節に注目してみれば$\alpha(G) \leq |C|(=2)$は必ず成立するので(各節に対応する頂点の部分集合からは、たかだか一つまでしか独立集合の要素をとりえない)、これはMISとなっていて、左側の条件を満たしている。
ここで、MISにとった頂点に対応する変数xに1を代入して($v_{12} \rightarrow x_{2} = 1,v_{21} \rightarrow \overline{x}_{1} = 1$)、$\psi$を確認してみると
$$ {\psi=(0 \lor 1 \lor \overline{x_3})\land(1 \lor x_3 \lor 1)} $$
となっており、これは$x_3$の値に関わらずTrueとなる。なぜならば、$\psi$がTrueとなるときは各節で少なくとも一つのリテラルがTrueであればよいからだ。また上述のグラフ作成における手順4での操作により、$x$と$\overline{x}$が同時に1になるような矛盾は起こらないようになっている。このように考えると、各節に対応する頂点の部分集合から頂点を一つ独立集合に持ってこれるとき、各節で少なくとも一つのリテラルをTrueにできることと対応していることが分かる。
$\alpha(G)=|C| \Leftarrow \psi=\text{True} $ の説明
今度は適当に$x_1=1,x_2=1,x_3=1$となっている場合を考えよう。
$$ {\psi =(1 \lor 1 \lor 0)\land(0 \lor 1 \lor 1)=True} $$
これは右側の条件を満たしているので、ここで各節からx=1となっているものと対応する頂点を適当に一つずつ選ぶ。例えば$v_{11},v_{23}$としよう。このとき各節から一つずつ対応する頂点を選んでいるので、当然これらの頂点は節の数だけ存在し、$x=1$ であれば必ず$\overline{x}=0$となるような論理的な対応が発生するので選んだ頂点は辺で結ばれていることはなく、必ず独立集合の要素にすることができ、なおかつMISともなっている。
このように考えると、$\psi$がTrueになっている時点で各節から少なくとも一つの頂点を選んで、MISの形成が可能なことが保証されていることがわかる。
$k$-SATの場合
定義
- リテラル: $L = \{x_1,x_2,…,x_n,\overline{x_1},\overline{x_2},…,\overline{x_n}\}, x \in {0,1}$
- 頂点: $v_i \in V, v_i$に対応する変数$y_i \in L, 1 \leq i \leq n$、特に節$c_p$の左からq番目のyと対応する頂点は$v_{p,q} = v_{3(p-1)+q}\ \ \ (v_1 = v_{1,1},v_2 = v_{1,2},v_3 = v_{1,3},v_4 = v_{2,1},…,v_n = v_{m,k(m)})$
- 節: $c_i = v_{i,1} \lor v_{i,2} \lor … \lor v_{i,k},1 \leq i \leq m,1 \leq k(i)\\$
- 論理式: $\psi = c_1 \land c_2 \land … \land c_m\\$
- 独立集合: $V’ \subseteq V$
グラフ作成の手順
- 各頂点vがとる変数xを対応させたグラフGを描く。
- 各節に対応する頂点の部分集合に属するv同士を辺で繋ぐ。
- $y_{p,q} = \overline{y_{p,q}}$となるようなv同士を辺で繋ぐ。
以上の手順により、上図のような正多角形の頂点を持つ完全グラフ同士が繋がったようなイメージで論理式に対応するグラフ$G(V,E)$は完成する。
定式化
ここで作成したグラフ$G(V,E)$に対しMIS問題を考えるのだが、前述したようにこの補グラフに対する最大クリーク問題を考えると、
/T-Wave/?p=97
この解説のような定式化が可能である。すなわち次のよう。
$$ y_i = \begin{cases} 1 & (if \hspace{5pt} v_i \in V’)\\ 0 & (otherwise) \end{cases} $$
$$ \mathrm{Obj}(\mathbf{y}) = -A \sum^n_{i=1}y_i + B \sum_{\{v_i,v_j\} \in E}y_i y_j $$
実装は極めてシンプルで、独立集合に含まれる頂点数が多いほど目的関数は小さくなり、辺で結ばれているような二つの頂点を同時に独立集合へ含めようとした時に目的関数が大きくなる罰金項をもつ($\{v_i,v_j\}$はこの2頂点をつなぐ辺を表す)。ここでは頂点に重みを考えないので正の定数$A, B$で考えれば良い。
以上においてMISの大きさを求めた時、$\alpha(G) = m$となるような$x$の組み合わせが求める解となる。
まとめ
今回はSATをMIS問題を経由してQUBOの形で定式化することを目標とし、簡単な例の場合においてSATがMIS問題へ還元可能なことを説明した。SATに関しては他にも補助変数を用いてAND,OR,NOTを実装して解く解法なども考えられるのでそちらも各自参照すると良い。
今後行いたいこと
- QAを用いた画像圧縮の論文を読むこと
- Quantum computingの本を読む
本記事の担当者
小林友明(編集:観山正道)

