文献情報
- タイトル:Comparing Three Generations of D-Wave Quantum Annealers for Minor Embedded Combinatorial Optimization Problems
- 著者:Elijah Pelofske
- 書誌情報:arXiv:2301.03009
概要
2023年5月31日をもって、約5年間利用されてきたD-Wave 2000Qが廃止となりました。現在はD-Wave Advantage、そして2023-2024年に発売予定のD-Wave Advantage2のプロトタイプが利用可能です。本論文では、最大クリーク問題、最大カット問題を解くことにより、これら3世代のマシンの性能比較を行っています。その結果、最新のAdvantage2が、最適解に近い解を得られる確率において最も優れていることが分かりました。これはハードウェアグラフが密になり、マイナー埋め込みに必要なチェーンが少なくなったことが一因と考えられます。また、Advantage2では、比較的フェアサンプリングしていないことも分かりました。
マシンの詳細
このセクションでは、D-Waveマシンの世代間の違いを說明します。その次に、ベンチマークで使用する最大クリーク問題、最大カット問題について紹介します。
世代間の差異

表1: マシンのスペック比較, [引用]arXiv:2301.03009
実験方法
実験では、NP困難である「最大クリーク問題」と「最大カット問題」を解くことで比較を行います。
まずは、これらの最適化問題を簡単に紹介します。
最大クリーク問題
クリークとは、任意の2頂点間にエッジがある頂点集合です。今回はノードの重み無しなので、ノードの数が最大になるようなクリークを求める問題となります。
最大クリーク問題のコスト関数は、以下のように記述されます。
$$
\tag{1}
H(\boldsymbol{x}) = -A\sum_{i \in V}x_{i} + B\sum_{(u, v)\in \tilde{E}}x_{u}x_{v}
$$
ここで、$x_{i} \in \{0, 1 \}$はバイナリ変数で、クリークに含まれる時に1を取ります。$\tilde{E}$はエッジの補集合で、$A, B$はハイパーパラメータです。第1項は、クリークのノード数が最大となるように設計されています。第2項では、エッジが繋がっていない2つのノードがクリークに含まれると、ペナルティとしてコストがプラスになります。
最大カット問題
最大カット問題とは、グラフのノードを2つのグループに分ける(エッジをカットする)際に、エッジの重みの和が最大となる組合せを探索する問題です。本論文はエッジ重み無しのため、カットするエッジの数が最大となるような組合せを探します。コスト関数は、次のように記述されます。
$$
\tag{2}
H(\boldsymbol{x}) = – \sum_{(u, v)\in E} (1 – x_{u}x_{v})
$$
ここで、$x_{u} \in \{ -1, +1 \}$はイジング変数です。$x_{u}$と$x_{v}$が同じグループの場合($x_{u} \ne x_{v}$)、エッジはカットしないのでコストには0が加算されます。一方で、$x_{u}$と$x_{v}$が異なるグループの場合$x_{u} = x_{v}$、エッジがカットされて、コストは-2加算されます。このようにして、コスト関数が最小となるようなイジング変数の組合せを探索します。
これで、解くべき問題の說明は終わりです。次は、問題設定について說明します。
問題設定
最大クリーク問題では200個、最大カット問題では150個のランダムグラフを解きます。ノード数は52です。比較指標として、各インスタンスに対して出力された1000サンプルの「mean approximation ratio」を使用します。これは、「1000サンプルのエネルギーの平均 / 基底状態のエネルギー」として計算しています。従って、1に近いほど精度高く求解出来ていると言えます。また、0の場合、最適解を見つけられなかったことを意味します。
もう1つの評価指標として、「chain break ratio」を使用します。これは、マイナー埋め込みをした際に生じる「チェーン」が壊れた割合を意味します。チェーンが壊れた場合、チェーン内の量子ビットの投票に基づいて値が決定されます。従って、chain break ratio が高いほど、最適解を見つけにくくなります。
また、D-Waveマシンには様々な内部パラメータが存在しますが、今回調整するのは「annealing time」と「chain strength」のみとしています。それ以外のパラメータは基本的にデフォルトとしています。
結果
まずは、テスト用のランダムグラフに対して、最適解を得られた確率を表2に示します。最大クリーク問題では、annealing timeとchain strenghをうまく調整した場合、4つのデバイスで全てのテスト問題における最大クリークを見つけることが出来たようです。一方、最大カット問題では、最適解を見つけられない問題もあったようです。また、最新機種よりもAdvantage system4.1が最も良いというのは驚きの結果です。
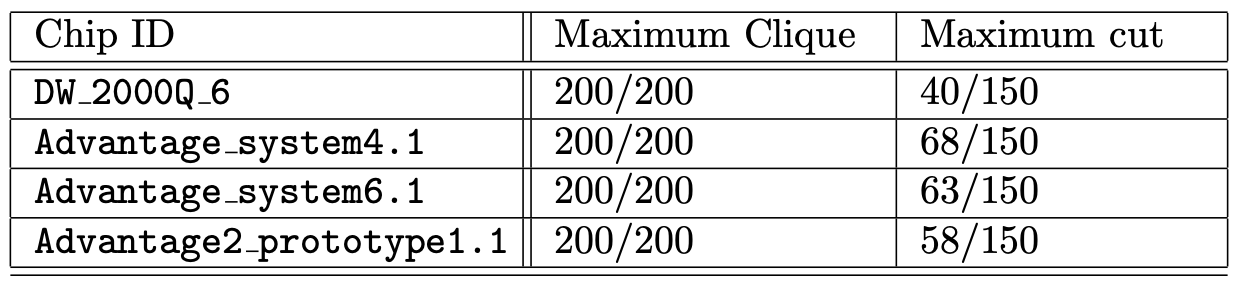
表2: 最適解を見つけられた割合, [引用]arXiv:2301.03009
図1は、最大クリーク問題の結果です。左の列から順に、D-Wave 2000Q, Advantage system4.1, Advantage system6.1, Advantage prototype1.1となっています。そして、上の行から順に、annealing timeが$2000 \mu s, 1000 \mu s, 100 \mu s, 10 \mu s, 1 \mu s$と設定した結果です。縦軸は「mean approximation ratio」であり、横軸は「chain stlength」となっています。各図には10色の線がプロットされており、これらはグラフ密度の違いを表しています。
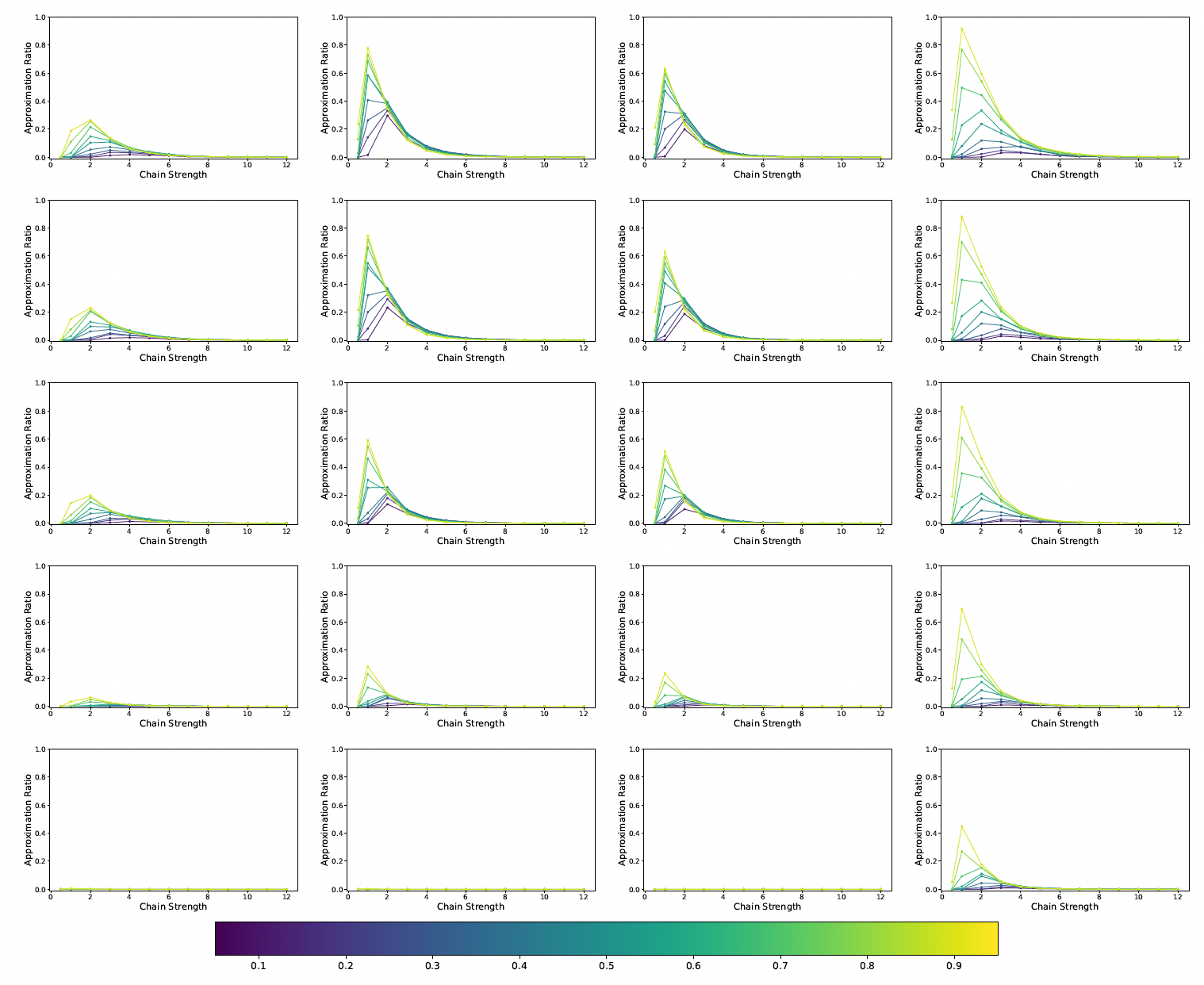
図1: 最大クリーク問題における「mean approximation ratio」と「chain strength」の関係, [引用] arXiv:2301.03009
続いて、最大クリーク問題におけるチェーンが壊れた割合を図4に示します。図の見方は、図3と同様です。
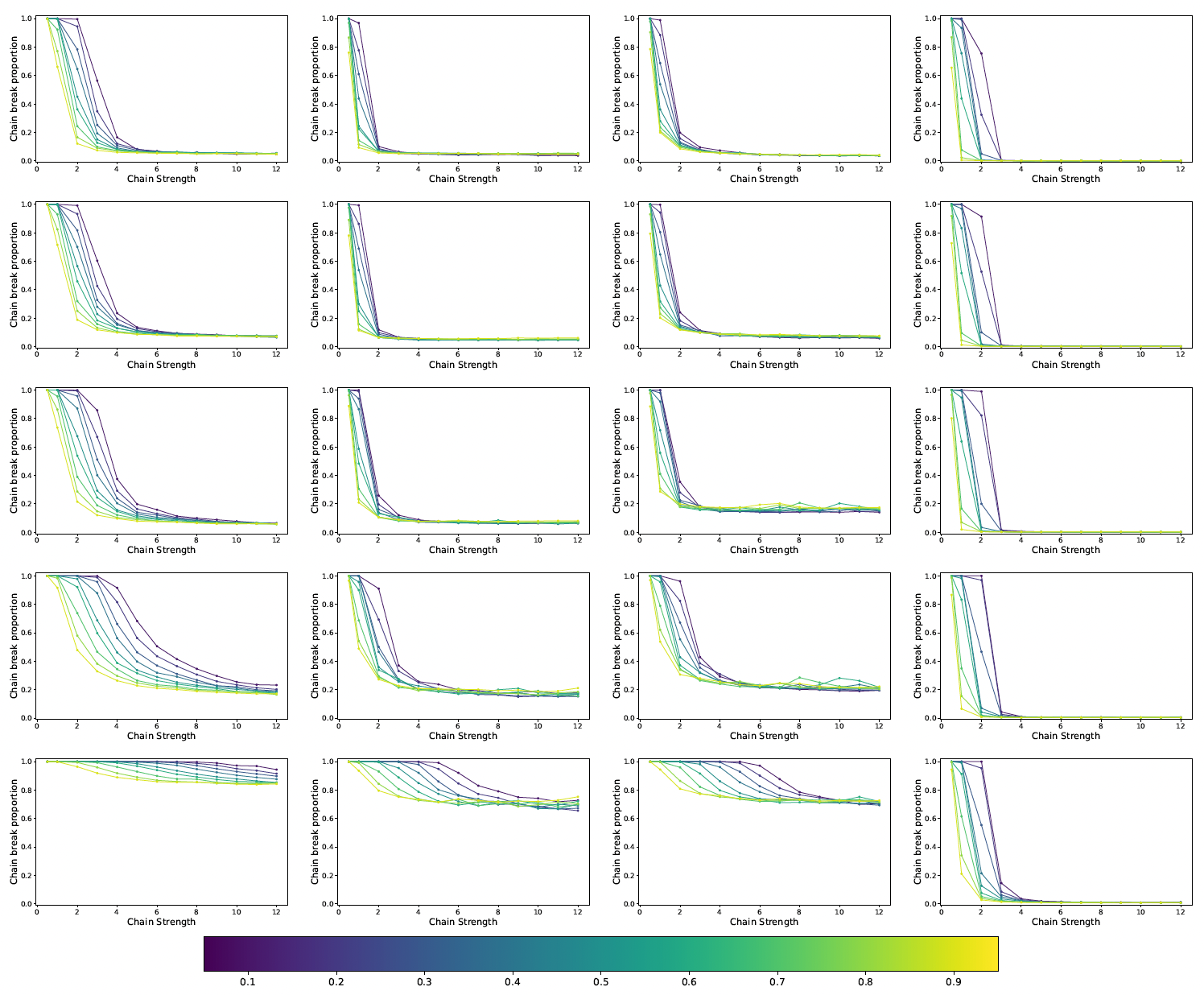
図2: 最大クリーク問題における「Chain break proportion」と「chain strength」の関係, [引用] arXiv:2301.03009
次は、最大カット問題についての結果を示します。まずは、「mean approximation ratio」の関係を図3に示します。
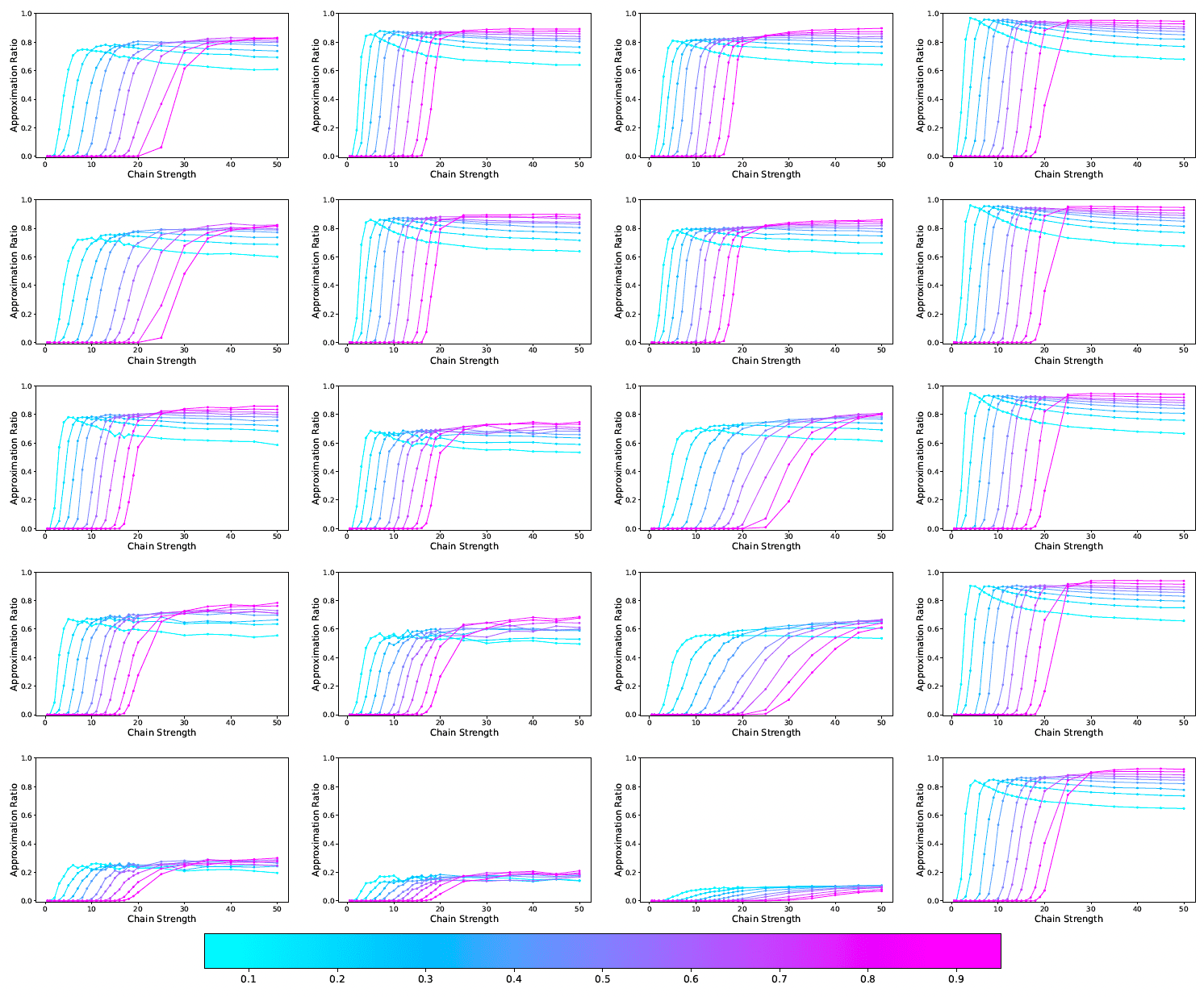
図3:最大カット問題における「mean approximation ratio」と「chain strength」の関係, [引用] arXiv:2301.03009
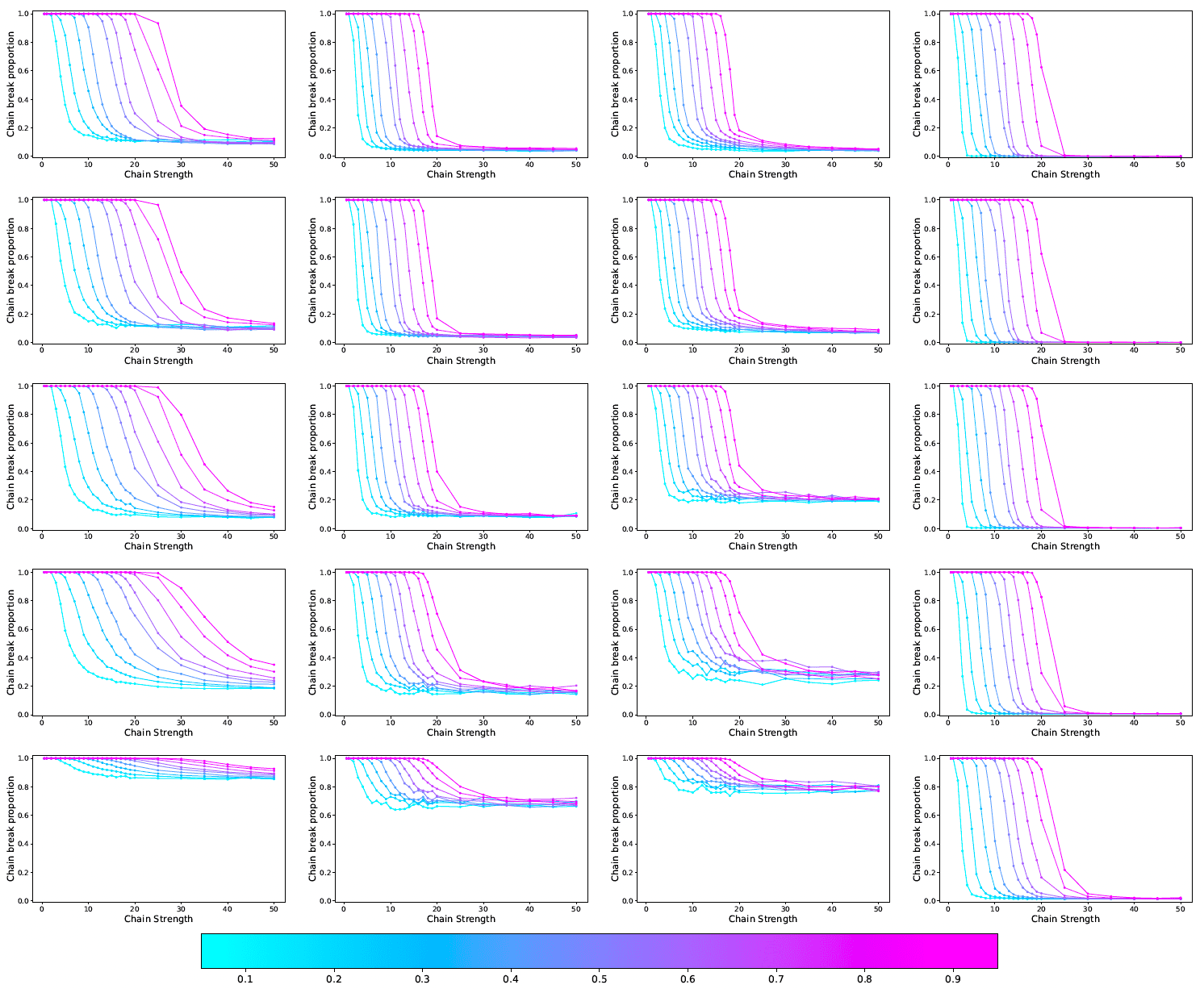
図4:最大カット問題における「Chain break proportion」と「chain strength」の関係, [引用] arXiv:2301.03009
フェアサンプリング
最後に、D-Waveマシンが最適解を等しい確率で得られていない(フェアサンプリングしていない)か検証します。量子アニーリングは、理論的にはフェアサンプリングしないことが知られています。D-Waveマシンが理想的な量子アニーリングを再現出来ているのか評価するためには、この指標が重要になってきます。
検証は次のような手順で行います。まず、あるインスタンスについて、最適解が得られる確率が最も高くなるようなパラメータ(annealing time、chain strength)をデバイス毎に探索します。ここで、得られるパラメータセットの数は複数になる可能性があることに注意して下さい。そして、そのパラメータ毎に得られるサンプルから、情報エントロピーを計算します。
情報エントロピーは以下のように表されます。
$$
\tag{3}
H(p) = -\sum_{i} p_{i}\log{p_{i}}
$$
ここで、$p_{i}$は$i$番目の最適解が得られる確率です。情報エントロピーが大きいほど、フェアサンプリングが出来ているということになります。具体例で示しましょう。
ある問題において、最適解Aと最適解Bがあるとします。これらが50%, 50%の等確率で得られたとしましょう。この時、情報エントロピーは、
$$
H(p) = -[0.5\log{0.5}+0.5\log{0.5}] \approx 0.693
$$
となります。次に、90%, 10%のような確率に偏りがある場合を計算してみましょう。
$$
H(p) = -[0.9\log{0.9}+0.1\log{0.1}] \approx 0.325
$$
となります。最後に、次に、100%, 0%の場合を計算しましょう。
$$
H(p) = -[1.0\log{1.0}] \approx 0
$$
このように、最適解が等確率で得られるほど、情報エントロピーは高くなります。一方で、完全に偏った確率の場合、情報エントロピーは0となります。以上を踏まえた上で、結果を図5で確認しましょう。

図5: フェアサンプリングの検証, [引用] arXiv:2301.03009
まとめ
本論文では、最大クリーク問題、最大カット問題を解くことにより、D-Waveの3世代のマシンにおける性能比較を行いました。Advantage2では、前世代に比べて埋め込みがしやすくなったこともあり、エネルギーの低い解が得られやすいことが分かりました。一方で、最適解を得られる確率は、問題によってはAdvantageの方が高い場合があるということも分かりました(表2)。また、最新機種はチェーンも壊れにくいことも分かりました。これらの結果は、アニーリング時間が短いほど顕著に現れていました。そして、フェアサンプリングについても比較検証を行いました。Advantage2は、Advantageよりもフェアサンプリングしていないことが分かりました。これは、Advantage2がAdvantageに比べて、ノイズの影響が少ないことが要因だと考えられています。
あとがき
この論文を選んだ理由は、Advantage system4.1と6.2の違いを知りたかったからです。表1から分かるように、スペックの差はほとんどないように思えます。結果を見ても、デバイス間の違いは分かりませんでした。従って、サンプラーを選ぶ際、どちらを選んでも結果はあまり変わらないと考えられます。一方で、プロトタイプではありますが、Advantage2は明らかに性能が向上していました。Advantage2が正式にリリースされると、これまでより大きい問題サイズが扱えるようになり、より高い確率で最適解を得られるようになるでしょう。
本記事の作成者
鹿内怜央