T-QARD Harbor

PyQUBO によるアニーリングマシン利活用の効率化

今回は、（株）リクルートコミュニケーションズが開発し、オープンソースにより公開されたドメイン固有言語 PyQUBO (プレスリリース) を紹介する。PyQUBO
は、組合せ最適化問題を制約なし二値変数二次計画問題 (QUBO)の形に定式化した後、D-Waveマシンや富士通デジタルアニーラといったイジングマシンに載せるために必要な問題データの変換を極めて簡略化するためのツールセットである。本記事では、量子アニーリングマシン利活用におけるミドルウェア開発事例を体感していただくために、Karpの21の問題の一つである最小頂点被覆問題のソルバーアプリケーションを作るという具体例を通して、従来のD-Wave SAPIを用いたプログラミングスタイルとPyQUBOを用いたそれとを比較する。

PyQUBO

（株）リクルートコミュニケーションズは、ドメイン固有言語『PyQUBO』を2018年9月25日にオープンソース (GitHub: recruit-communications/pyqubo)
として公開した。定式化した組合せ最適化問題をアニーリングマシンで解くために、QUBO (Quadratic Unconstrained Binary Optimization: 制約なし二値変数二次計画問題) やイジングモデルといった形式に変換する必要がある。PyQUBOを使用することで、この変換を自動的に行うことが可能となる。D-Wave Ocean SDKのホームページにも、サードパーティソフトウェアとして掲載されている。

PyQUBOのオンラインドキュメントには、PyQUBOの特徴として以下の4つが挙げられている。

  • Pythonがベースとなっている
  • QUBOの生成を速く行える
  • 制約の自動バリデーション
  • パラメータチューニングのためのプレースホルダー

D-Wave Sysemsが提供しているD-Wave Ocean SDK (GitHub:
dwavesystems/dwave-ocean-sdk)がPythonで使用できるように、D-Waveマシンでの開発はPythonで行なう場合が多く、PyQUBOもその名の通りPythonで利用可能となっている。その他の特徴については、この後詳しく述べていく。

PyQUBOのインストール方法

PyQUBOがサポートしているPythonのバージョンは、2.7, 3.4, 3.5, 3.6, 3.7
である。PyQUBOをインストールするには、pip(Pythonのパッケージ管理システム)を用いるか、PyQUBOのgitリポジトリからインストーラをダウンロードする。

# pipを使用する場合
% pip install pyqubo

# gitリポジトリからインストーラをダウンロードする
% git clone https://github.com/recruit-communications/pyqubo
% python setup.py install

また、PyQUBO、D-Wave Ocean SDKと依存性のあるライブラリは、それぞれ以下の通りである。

# pyqubo==0.1.1
# https://github.com/recruit-communications/pyqubo/blob/master/setup.py
dimod>=0.7.4
numpy>=1.14.0,<2.0.0
six>=1.10.0,<2.0.0
dwave-neal>=0.4.2

# dwave-ocean-sdk==1.0.3
# https://github.com/dwavesystems/dwave-ocean-sdk/blob/master/setup.py
dwave-networkx>=0.6.1,<0.7.0
dwave-system>=0.5.0,<0.6.0
dwave-qbsolv>=0.2.7,<0.3.0
dwave-neal>=0.4.0,<0.5.0

本記事のコード

以下では実際のコードを交えて、PyQUBOの使い方と従来の場合との違いを説明する。
https://gist.github.com/t-qard/t-wave

アニーリングマシンによる問題解決

アニーリングソルバーが適用できる組合せ最適化に限らず、数理最適化は以下のような手順で行われる。

最適化問題解決の流れ
最適化問題解決の流れ

アニーリングマシンによる最適化の特徴は、このうちの最適化手法にある。古典アルゴリズムによる最適化では、問題の数理モデルがどの問題クラスに属するのかを検討し、適切なアルゴリズムを選択する。これまで考案されてきた様々なアルゴリズムの中から問題に適したものを探す、あるいは新たに開発して、厳密解あるいは良い性質を持つ近似解を得る。

一方、アニーリングマシンで問題を解くには、定式化した問題をQUBOまたはイジングモデルという形式に変換しさえすれば、ひとまずなんらかの近似解を得ることは可能だ。たとえば、D-Waveマシンのような量子アニーリングマシンは極めて短時間に多数の近似解を得られる。この中から所望の目的を達成するに相応しい解を後処理の形で選び取るというのが基本的な戦略だ。

単なる動作速度だけでなく、理論的性能評価に裏付けられたソルバーが存在しない問題に対しても素早い開発とその実証実験を行うことが可能となるという点をまず、意識していただきたい。

一般的な最適化計算とアニーリングマシン
一般的な最適化計算とアニーリングマシン

さて、この記事のテーマであるPyQUBOの利点を述べるために、QUBO(またはイジングモデル)への変換に着目する。以下の図は、その過程の概要である。実際には、アニーリングスケジュールの調整や埋め込みの見直し、古典コンピュータとの相補的な使用を考えるといった工程も存在する。

従来の場合とPyQUBOの比較
従来の場合とPyQUBOの比較

先ほど述べたとおり、PyQUBOの特徴の一つにプレースホルダーがある。QUBOのUが”制約なし”を意味するように、制約条件をラグランジュの未定乗数項としてコスト関数に組み込む。その際に各制約項の重みとなるパラメータを設定する。プレースホルダーは、このパラメータを一時的に保管するためのものであるため、コスト関数の各項を計算した後にプレースホルダーの値を変えることで、パラメータの調整が簡便になる。これまでは自分で実装しない限りは、何度も各項の計算を行なっていた。しかし、問題によってはその計算量が大きく、繰り返すことが困難である場合がある。

また残りの特徴として、得られた結果が制約条件を満たすかどうかを自動的にチェックするメソッドが存在する。これまでは、このような判定を行なうために、自らコードを書く必要があった。PyQUBOでは、解が制約を満たすか否かの簡単な判定をすぐに行える。以下のコードは、PyQUBOのオンラインドキュメントにある制約の自動バリデーションの例である。decode_solutionメソッドの戻り値として、Pythonの辞書型で情報が得られる。

>>> decoded_solution, broken, energy = model.decode_solution(raw_solution, vartype='BINARY')
>>> pprint(broken)
{'a+b=1': {'penalty': 1.0, 'result': {'a': 1, 'b': 1}}}

もちろん、解の後処理、可視化といった部分は人が行なう必要があるものの、即座に判定を行いたい場面が実際にはあり、非常に有用である。

頂点被覆問題

頂点被覆とは

あるグラフ $G(V,E)$ を考える。$V$ の部分集合$V’$が $G$ の辺を頂点被覆するというのは、すべての辺のいずれかの端点が
$V’$ に含まれることである。以下に、簡単な例を示す。ここでは分かりやすくするため、上の図のように$V’$に属する頂点を彩色している。

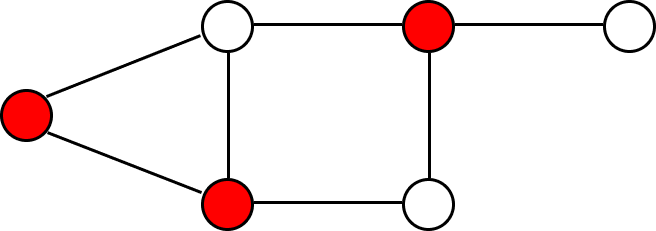
頂点被覆問題の例
頂点被覆の例

頂点被覆問題の定式化

最小頂点被覆問題では、部分集合$V’$の要素数が最小となるものを求めるを考える。
彩色する頂点数($V’$に属する頂点数)を最小化するため、これがコスト関数の主な項となる。

$$ H_\mathrm{vertices} = \sum_{v} x_v \tag{1} $$

また、各辺のいずれかの端点は彩色される($V’$に属する)という制約を、制約項として加える。

$$ H_\mathrm{cover} = \lambda_\mathrm{cover} \sum_{(u,v) \in E} \left( 1-x_{u} \right) \left( 1-x_{v} \right) \tag{2} $$

最小頂点被覆問題のコスト関数は、以下のようになる。

$$ H = H_\mathrm{cover} + H_\mathrm{vertices} \tag{3} $$

QUBOへの変換

では実際に、先ほど定式化した問題をQUBOへ変換を行なっていく。ここでは、先ほどのグラフを対象として問題を解く。

# 問題設定
NUM_VER = 6
vertices = list(range(NUM_VER))
edges = [(0,1), (0,4), (0,5), (1,2), (1,3), (3,4), (4,5)]

PyQUBOを用いた場合

以下のコードでは、PyQUBOによってQUBOへの変換を行っている。

from pyqubo import Array, Constraint, Placeholder, solve_qubo

# BINARY変数
x = Array.create('x', shape=NUM_VER, vartype='BINARY')

# QUBO形式で定式化
H_cover = Constraint(sum((1-x[u])*(1-x[v]) for (u,v) in edges), "cover")
H_vertices = sum(x)
H = H_vertices + Placeholder("cover") * H_cover

# モデルをコンパイル
model = H.compile()

# プレースホルダーに具体的な数値を当てはめて、QUBOを作成
feed_dict = {"cover": 1.0}
qubo, offset = model.to_qubo(feed_dict=feed_dict)

従来の場合

一方、以下のコードはこれまでの方法である。(Pythonにはリスト内包表記などがあるが、読みやすいコードにしている)

# 係数行列
h = [0] * NUM_VER
J = {}
S = {}

# 制約項のパラメータ
param_cover = 1.0

for u in range(NUM_VER):
    h[u] = -2*param_cover + 1
    for v in range(u+1, NUM_VER):
        if (u,v) in edges:
            J[u,v] = param_cover

比較・評価

上記のコードを踏まえて、PyQUBOと従来の方法を比較・評価する。まずコードの量は問題のコスト関数に依存する。展開した式が長くなるのであれば、PyQUBOを用いた方が少ないコードの量で済むだろう(ただし、これはコードを書く人の技量にも大きく依存する)。

コードの可読性については、数式をほぼ直接表しているという点でPyQUBOの方が優れていると言える。その可読性から、実装する際に数値的なミスやバグが入る可能性も減らすことができる。

コスト関数とPyQUBOの対応
コスト関数とPyQUBOの対応

そして、私がPyQUBOを使用して最も大きな差異を感じたのは、それぞれ注目する部分が異なることである。従来の方法では係数行列$h$, $J$,
$Q$に、PyQUBOではコスト関数全体に注目している。QUBOを作成するコードを書くのは現在のところ人間であり、その人間の意識がどこに向かうかは重要である。

実際に問題を解く中で、係数行列を可視化しスパース性や係数の偏りなどを確認して、問題の特徴や方針を考える場面がある。従来の方法ではそれが自然に行われる。PyQUBOによる実装においても、実装されているメソッドを使用することで、係数行列を取得することは容易であり、係数行列を積極的に確認するべきである。また、PyQUBOが有用だからといってそれだけでよいと私は思っていない。なぜなら、これまでのようにコスト関数を変形する中で学べることが幾分あるからだ。

結果

PyQUBOには、SA(Simulated Annealing)が実装されており、PyQUBOだけでも組合せ最適化問題を解くことができる。D-Waveマシンに問題を投げる前に、小さな問題に対してSAを用いることで、コスト関数定式化や実装などが正しいかを容易に確かめることができる。以下、PyQUBOのSAを使用したコードを示す。

# SAで解を探索する
raw_solution = solve_qubo(qubo)

# 得られた結果をデコードする
decoded_solution, broken, energy = model.decode_solution(raw_solution, vartype="BINARY", feed_dict=feed_dict)

これによって、以下の解が得られた。

>>> pprint(decoded_solution)
{'x': {0: 1, 1: 1, 2: 1, 3: 0, 4: 1, 5: 0}}

また以下のコードは、PyQUBOで作成したQUBOをD-Wave Ocean SDKを用いて解くための一例である。PyQUBOで作成したQUBOをそのままD-Wave Ocean
SDKのsample_qubo()やsample_ising()に渡すことができる。

from dwave.system.samplers import DWaveSampler
from dwave.system.composites import EmbeddingComposite

sampler = EmbeddingComposite(DWaveSampler(endpoint=endpoint, token=token, solver=solver_name))
response = sampler.sample_qubo(qubo)

これによって、以下の解が得られた。

>>> pprint(response.sample_matrix)
array([[1, 1, 1, 1, 0, 1, 0]], dtype=int8)

補足

本記事で使用したクラス

この記事の中で紹介したコードで使用したクラスや関数をまとめた。ここでは、紹介しきれないほど有用なクラス、メソッドが用意されているため、詳細はPyQUBOのオンラインドキュメントを確認してほしい。

クラス、メソッド名概要
Arrayバイナリ変数、イジング変数の多次元配列。バージョン0.1.0よりVector,Matrixの代わりとなった。
Array.create()バイナリ変数、イジング変数をともに選択でき、次元数を指定できる。numpy.arrayを渡すことも可能。通常の最適化問題を解く際に頻繁に使用するであろうメソッド。
Constraintコスト関数の制約項を記述するためのクラス。これを用いることで、解のデコード時に制約条件のチェックが可能。
Express.compile()記述したコスト関数をモデルにコンパイルするためのメソッド。
Model.to_qubo()モデルをQUBOに変換するためのメソッド。あらかじめ設定したPlaceholderをdict形式で渡す。
Model.decode_solution()得られた解をデコードするためのメソッド。デコードした解に加えて、制約をチェックした結果とエネルギー値が返される。
Placeholderコスト関数の各項のパラメータを記述するためのクラス。これによって、何度もコンパイルする必要がなくなり、パラメータ調整が効率的になる。
solve_qubo()SAでQUBOを解くための関数。同様に、イジングモデルをSAで解くための関数solve_ising()も用意されている。

pickleによるモデルの保存

ここでは、作成したQUBOデータの保存方法の一例を紹介する。従来の方法では、h,J,Qといった係数行列を計算することが主な前工程であり、それらのデータはcsv形式などでファイルに保存し、保管・共有を行なう。一方で、PyQUBOの場合、Pythonの標準ライブラリpickleを用いて、Pythonオブジェクトの直列化ができる。つまり、作成した各項やコスト関数全体のデータをバイトストリームとして、ファイルの入出力が可能となる。以下のコードは、その一例である。

# モデルをコンパイル
model = H.compile()

# モデルをpickleで保存
with open('model.pickle', 'wb') as f:
    pickle.dump(model, f)

# pickleで保存したモデルを読み込む
with open('model.pickle', 'rb') as f:
    loaded_model = pickle.load(f)

正規化

自分が確認した範囲では、PyQUBOには係数行列を正規化するようなメソッド、関数が存在しない。しかし、組み合わせ最適化問題の中には、各項でオーダーが大きく異なる場合が少なくない。例えば、ロジスティックにおける巡回セールスマン問題では運送コストが大きな値をとる場合があり、正規化することで他の制約項が作用するようにする必要がある。以下のコードは、各項を正規化するための関数の一例である。

import numpy as np

# 各項を正規化する関数
def normalize(exp, var_type='SPIN'):
    if var_type != 'SPIN' and var_type != 'BINARY':  # 変数のタイプがイジング・QUBO表現でない場合、終了
        raise ValueError("var_type must be 'SPIN' or 'BINARY'.")
 
    model = exp.compile()
    if var_type == 'SPIN':
        compiled_h, compiled_J, offset = model.to_ising()
        norm = max(np.max(np.abs(list(compiled_h.values()))),
                   np.max(np.abs(list(compiled_J.values()))))

    else:
        compiled_qubo, offset = model.to_qubo()
        norm = np.max(np.abs(list(compiled_qubo.values())))

    # 絶対値が最大の係数で各成分を割ることで、[0,1]に正規化
    return exp / norm

絶対値が最大の係数を取得するために、入力されたExpressオブジェクトをコンパイルしているが、他の求め方があるかもしれない。また、normalize関数の使用例は以下のようになる。上で述べた頂点被覆問題の制約項を正規化している。

# normalize関数の使用例(分かりやすくするため、変数で分けている)
exp = sum((1-x[u])*(1-x[v]) for (u,v) in edges)
normalized_exp = normalize(exp)
H_cover = Constraint(normalized_exp, "cover")

Sympyとの連携

コスト関数を発表スライドやJupter
Notebookに書くときに、少々面倒に感じるときがある。そこで、記号計算を行うPythonのライブラリSympyを用いて表示したコスト関数を、PyQUBOで利用可能な式に変換できないか考えた。簡単な例ではあるが、n個のQUBO変数$x_i$のうち1個のみ1をとる場合に値が最小となる、one-hot
encodingを紹介する。

from sympy import Symbol, Sum
init_printing()
import pyqubo
import re

# Sympyの数式をPyQUBO用の文字列に変換する
def sympy2pyqubo(exp_sympy):
    str_sympy = exp_sympy
    # Sum -> sum
    str_sympy = str_sympy.replace('S', 's')
    # 総和の範囲(*,*,*)をfor文に置き換える
    str_sympy = \
    re.sub(',\s*[^sum]\(\s*(.+)\s*,\s*(.+)\s*,\s*(.+)\s*\)\)', \
        ' for \\1 in range(\\2, \\3))', str_sympy)
    # 変数をリストに置き換える
    str_sympy = \
    re.sub('(.+?)_(.+?)', '\\1[\\2]', str_sympy)

    return str_sympy

# 変数
x = Symbol('x_i')
i = Symbol('i')
n = Symbol('n')

# Sympyで数式を定義
H = (Sum(x, (i, 1, n)) -1)**2
str_H = str(H)
print(str_H) # >>>(Sum(x_i, (i, 1, n)) - 1)**2

n = 10
x = pyqubo.Array.create("x_i", shape=n, vartype='SPIN')

H = eval(sympy2pyqubo(str_H))
print(H) # >>>((Spin(x_i[1])+Spin(x_i[2])+Spin(x_i[3]...

上記のコードでは、Sympyの式を文字列に変換し、総和の範囲を表す記述をPyQUBOのために書き換える。その後、eval()関数でPyQUBOとして評価している。

まとめ

頂点被覆問題を通して、QUBOの作成における従来の方法とPyQUBOの比較を行なった。PyQUBOはアニーリングマシンを組み合わせ最適化問題のソルバーとして利用する上で、開発・実験の効率化を進めることができる。オープンソースとして公開されているため、多くの開発者や研究者がPyQUBOを利用することを勧める。また、論理ゲートなどこの記事では紹介していない機能もあり、今後も利用を続けていこうと思う。

参考

T-WaveのGithub

本記事およびT-Waveで掲載しているコードは、以下のGithubリポジトリにて公開している。D-Waveマシンを利用するプログラムを順次公開しているので、ぜひ確認していただきたい。

Github: https://github.com/t-qard/t-wave

本記事の担当者

丸山尚貴

Post Views: 1,241

© 2018-2023 T-QARD: Center for Quantum Application Research and Development, Graduate School of Information Sciences, Tohoku University