N-クイーン問題とは
導入
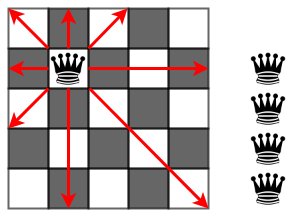
5 × 5マスのチェス盤に5個のクイーンをどのように置いたら、お互いの効きが当たらないか考えてみよう。クイーンは、縦横斜めに他の駒によって遮られない限り進める。
これを一般化した問題はN-クイーン問題 (N-Queens Problem)と呼ばれ、$N \times N$マスのチェス盤にN個のクイーンをお互いの効きが当たらないように配置する問題である。
さて、先ほどの場合の答えは分かっただろうか。もし分からなくても、愚直にクイーンの配置を試していけば見つかるかもしれない。しかし、クイーンの可能な配置は${}_{25} C _5=53,130$通り存在し、これには時間と忍耐力を要する。実際には、以下の2つの基本解が存在する。
また、基本解の回転と反転によるバリエーション解がある。左の基本解に対して回転と反転により8パターンの変形、右の基本解は点対称であるため2パターンの変形があり、合わせて10個のバリエーション解が見つかっている。$N=5$の場合であれば大したことはないが、Nが大きくなると解を見つけていくことが困難になることは想像に難くない。このように膨大な組み合わせが存在する問題については、動画「『フカシギの数え方』 おねえさんといっしょ！ みんなで数えてみよう！」が面白い。
これまでに見つかった解
人類がすべての解を見つけることができた最大の場合は、$N=27$である。
| N | 基本解 | バリエーション解 | 可能な配置数 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 0 | 0 | 6 |
| 3 | 0 | 0 | 84 |
| 4 | 1 | 2 | 1820 |
| 5 | 2 | 10 | 53130 |
| 6 | 1 | 4 | 1947792 |
| 7 | 6 | 40 | 85900584 |
| 8 | 12 | 92 | 4426165368 |
| 9 | 46 | 352 | 260887834350 |
| 10 | 92 | 724 | 17310309456440 |
| 11 | 341 | 2680 | 1276749965026536 |
| 12 | 1787 | 14200 | 103619293824707388 |
| 13 | 9233 | 73712 | 9176358300744339432 |
| 14 | 45752 | 365596 | 880530516383349192480 |
| 15 | 285053 | 2279184 | 91005567811177478095440 |
| 16 | 1846955 | 14772512 | 10078751602022313874633200 |
| 17 | 11977939 | 95815104 | 1190739044344491048895397910 |
| 18 | 83263591 | 666090624 | 149482492334195165714038760136 |
| 19 | 621012754 | 4968057848 | 19870867053543756004133247695400 |
| 20 | 4878666808 | 39029188884 | 2788360983670896737872851072994080 |
| 21 | 39333324973 | 314666222712 | 411887396336567398822620727355402190 |
| 22 | 336376244042 | 2691008701644 | 63887407766986865702182544710470036560 |
| 23 | 3029242658210 | 24233937684440 | 10381758958529585222885358558747563185920 |
| 24 | 28439272956934 | 227514171973736 | 1763783520005146433232953016554504214270600 |
| 25 | 275986683743434 | 2207893435808352 | 312690620414907617326451186807195415244296900 |
| 26 | 2789712466510289 | 22317699616364044 | 57746226578042013138408988185727715132037050952 |
| 27 | 29363791967678199 | 234907967154122528 | 11091107763254898773425731705373527055193637625824 |
歴史
N-クイーン問題の歴史は150年以上あり、チェスにおけるパズルとして始まった。
| 1848年 | チェスコンポーザー(チェスに関する問題を作成する人)のMax Bezzelが8-クイーン問題を発表した。 |
|---|---|
| 1850年 | Franz Nauckが8-クイーン問題の初めての解を発見。N-クイーン問題に拡張した。 |
これ以降、Carl Friedrich Gaussをはじめとする数学者がこれらの問題を研究の対象とし始めた。
| 1874年 | S.Guntherは解を求めるために、行列式を用いる方法を提案し、後にJWL Glaisherがその方法を改良した。 |
|---|---|
| 1972年 | Edsger Dijkstraは、この問題を題材として構造化プログラミングや深さ優先探索、バックトラックアルゴリズムを説明した。 |
| … | … |
| 2009年 | ドレスデン工科大学で、26-クイーン問題が計算された。 |
| 2016年 | Q27 Projectによって、27-クイーン問題が計算された。 |
本記事で行うこと
今回の記事では、
- 問題の定式化を変えることで、D-Waveマシンへの埋め込みや得られる結果にどのような違いが見られるか実験する
- 得られる解とエネルギー分布から、D-Waveマシンの特性を調べる
を主な目標とする。
D-Waveマシンによる実験
QUBO表現による問題の定式化
変数：$q_{i,j} \in \{0, 1\}$ (i行j列にクイーンが配置される場合に$1$, そうでなければ$0$)
制約条件は4つからなり、クイーンの総数に関する制約条件を異なる形で加えた場合を含む。
各行に配置するクイーンは1個のみ
$$ H_\mathrm{row} = \lambda_\mathrm{rowcol} \sum_{i=0}^{N-1} \left( 1-\sum_{j=0}^{N-1} q_{ij} \right)^2 \tag{1} $$各列に配置するクイーンは1個のみ
$$ H_\mathrm{column} = \lambda_\mathrm{rowcol} \sum_{j=0}^{N-1} \left( 1-\sum_{i=0}^{N-1} q_{ij} \right)^2 \tag{2} $$行と列の制約項については、他の組合せ最適化問題にもよく表れる形のため説明は割愛する。
(例えば、「宮城県の市区町村を塗り分けろ – グラフ彩色問題 をD-Waveマシンで解く」を参照)
斜めに配置するクイーンは0または1個のみ
$$ \begin{aligned} & H_\mathrm{diagonal} \\ &= \lambda_\mathrm{diagonal} \left( \sum_{s=1}^{2N-3} \left(\frac{1}{2}-\sum_{i,j;i+j = s} q_{ij} \right)^2 + \sum_{s=-\lfloor \frac{2N-3}{2} \rfloor}^{\lfloor \frac{2N-3}{2} \rfloor} \left(\frac{1}{2}-\sum_{i,j;i-j = s} q_{ij} \right)^2 \right) \tag{3} \end{aligned} $$それぞれの斜めに配置するクイーンの数が0または1のときに限り、式(3)の2乗の部分が最小値$\frac{1}{4}$となるようにしている。
N個のクイーンを配置する
[1]クイーンの総数をなるべくNに近づける
素朴に2乗の項を用いて、クイーンの総数がNのときに最小値0となるようにする。
[2]クイーンの総数をなるべく多くする
他の制約が存在するため、このように単純にしても上手くいくと考えられる。
[3]制約項を加えず、行と列の制約を強くする
行と列の制約を満たす場合クイーンの総数はNとなるため、$H_{row}$と$H_{column}$の効きを強くする($\lambda_{rowcol}$の値を大きくする)。
注意として、今回考える場合以外にも様々な制約の与え方が存在する。なお、行と列は対称であるため、(1)と(2)の項には同じパラメータを設定する。同様に、2方向の斜めに関する部分も同じパラメータとする。
よって、最小化する目的関数は以下のようになる。
目的関数:
$$ H = H_\mathrm{row} + H_\mathrm{column} + H_\mathrm{diagonal} + H_\mathrm{queens} \tag{5} $$各制約を満たす場合の各項の値は、$H_{row}=0$、$H_{column}=0$、$H_{diagonal}=\frac{1}{2} \times \left( 2N-3\right) = N-\frac{3}{2}$、式(4-1),(4-3)のとき$H_{queens}=0$、式(4-2)のとき$H_{queens}=-N$である。よって、すべての制約を満たすときの目的関数のエネルギーは、式(4-1),(4-3)のとき$H=N-\frac{3}{2}$、式(4-2)のとき$H=-\frac{3}{2}$となる。
QUBO行列
D-Wave社が提供している埋め込みアルゴリズムを利用すると、$N=8$の場合における隣接行列は以下のようになった。式(4-1)の場合は、式(4-1)の$H_{queens}$からも分かるように全結合であり、必要な物理量子ビットの数が多くなる。式(4-2),(4-3)の場合、先ほどよりスパースであるが、対角成分付近にある行の制約部分が密な結合となっている。
参考までに、式(4-2),(4-3)の場合における隣接行列を以下に示す。ただし、クイーンの総数に関する制約項$H_{queens}$は対角成分のみである。
チェス盤の行と列は対称であるものの、上の図では行と列の成分に違いが見られる。これは、i行j列を表すイジング変数$x_{ij}$を$x_{i \times N + j}$のようにして、一次元で表しているためである。もちろん、行と列を入れ替えて$x_{j \times N + i}$としてもよく、隣接行列も入れ替わる。
埋め込み
$N=5$から$N=8$まで場合で、それぞれの定式化に対して必要な物理量子ビットの数を以下に示す。D-Waveが提供している埋め込み関数はヒューリスティックなアルゴリズムを用いているため、ここでは10回の平均値を算出した。
表: 埋め込みに必要な物理量子ビットの数(10回の平均値)
| N | 5 | 6 | 7 | 8 |
|---|---|---|---|---|
| 式(4-1)による定式化の場合 | 251 | 531 | 988 | 1710 |
| 式(4-2),(4-3)による定式化の場合 | 204 | 453 | 917 | 1557 |
各項のパラメータ
D-Wave 2000Qをソルバーとし、SAPI(D-WaveのAPI)を用いてそれぞれの定式化における解を求めた。アニーリング回数は100回と1000回で行なった。また、各項のパラメータを変えながら基底状態が多く得られる場合を探し、以下のように設定した。ただし、今回試した中で最も良かった値を設定しており、最適な値とは限らない。
表: 設定した各項のパラメータ
| 各項のパラメータ | $\lambda_{rowcol}$ | $\lambda_{diagonal}$ | $\lambda_{queens}$ |
|---|---|---|---|
| 式(4-1)の場合 | 2 | 2 | 1 |
| 式(4-2)の場合 | 1.4 | 1.2 | 1 |
| 式(4-3)の場合 | 1.7 | 1 | – |
結果
成功例・失敗例
ひとまず、得られた結果を見てみよう。式(4-2)の制約項による場合において100回アニーリングを行なった場合の、基本解(a)と(b)、失敗例(c)を示す。失敗例(c)は、図中8行目にクイーンが配置されておらず、6行目に2個のクイーンが配置されているため、行に関する制約を満たしていない。
また、得られた結果の中にバリエーション解が存在した。上記の図(a)のバリエーション解を以下に示す。図(a)の反転と90度の回転によって図(d)が得られ、図(e)がそのバリエーション解であることが確認できる。
いくつか解は得られたのだが、そもそも量子アニーリングに基づいているD-Waveマシンは組合せ最適化問題の近似解法であり、この問題のすべての基本解やバリエーション解を厳密に得ることを目的としている訳ではない。上記の表にあるような膨大な可能性の中から、古典コンピュータにおけるアルゴリズムよりも速く最適解を得られることを期待し、D-Waveマシンを使用している。
エネルギーの分布
先ほど示したように、D-Waveマシンから返ってくる結果にはすべての制約を満たすものとそうでないものが含まれる。また、それぞれの解に対するエネルギーのや同じエネルギーの解がいくつ含まれるかといった、様々な情報が得られる。
そこで、得られた結果のエネルギー分布を見てみよう。エネルギーの値を見ることによっても、各制約を満たしているかどうかが分かる。以下の図は、D-Waveマシンから直接返されたエネルギーのヒストグラムである。式(4-3)の場合を除き、アニーリング回数を増やすことでエネルギーの低い度数が多くなっており、エネルギーのより低い解を得られていることが分かる。
得られた解、つまり$x_{ij}$の値を目的関数に代入することで、目的関数のエネルギーを計算することができる。ちなみに先ほど示したエネルギーは、D-Waveマシン上での埋め込みに対するエネルギーである。
以下の図は、それぞれの定式化における目的関数のエネルギーのヒストグラムを示している。なお、基底状態のエネルギーは、式(4-1)と式(4-3)のときに-6.5、式(4-2)のときに-1.5となる(各図における左端のエネルギー)。
式(4-2)の場合ではエネルギーが様々な値をとっている一方で、式(4-1)と式(4-3)の場合ではエネルギーが特定の値にまとまっている。これはクイーンの総数に関する制約について、式(4-1)より式(4-2)の方が緩い制約であることによると考えられる。ここでは示していないが、異なるパラメータの設定で実験した場合では、同じエネルギーの値に対して異なる割合で分布していた。
これまで示した結果の中には、2つ以上の異なった解が同じエネルギーをとることがあった。物理学において、ハミルトニアン(先ほどの目的関数のこと)が同じエネルギー準位をとることを縮退(degeneracy)という。物理的状態が縮退している場合、その状態は対称性をもっていることが多く、N-クイーン問題においては基本解に加えて対称性によるバリエーション解がある。そこで、上の図のようなエネルギー分布に対して、クイーンがどのような配置となっているのか気になってくる。
基底状態のエネルギーと解
前節の結果において、基底状態のエネルギー分布に対するクイーンの配置を以下に示す。式(4-1)の場合、得られた解に多様さがほとんどなく、アニーリング回数を増やすとそれが顕著に表れた。
式(4-1)の場合における解とエネルギーの割合(100回アニーリングした場合)
式(4-1)の場合における解とエネルギーの割合(1000回アニーリングした場合)
式(4-2)の場合、式(4-1)の場合よりも多種類の解が得られた。またアニーリング回数を増やすことでも、解の種類を増えているることが分かる。
アニーリング回数が100のとき、解(a)の方が解(b)よりも多く得られたが、アニーリング回数を1000にすると、解(b)の方が解(a)よりも多く得られた。アニーリング回数によって得られる各解の個数が変化することは興味深い。
式(4-2)の場合における解とエネルギーの割合(100回アニーリングした場合)
式(4-2)の場合における解とエネルギーの割合(1000回アニーリングした場合)
式(4-3)の場合、式(4-2)よりもさらに多種類の解が得られた。同様にアニーリング回数を増やすことで、得られる解のバリエーションが増えている。そして、割合の小さい解は割愛しているが、得られた解の中で様々なバリエーション解が得られていた(少々分かりづらいが、下の図の中にもバリエーション解がある)。
式(4-3)の場合における解とエネルギーの割合(100回アニーリングした場合)
式(4-3)の場合における解とエネルギーの割合(1000回アニーリングした場合)
ここまで、単に解にのみ注目するのではなく、そのエネルギー分布、エネルギーと解の関係を見てきた。
以降はおまけとして、問題の特徴を考慮する、そしてNがより大きな問題を解くことを試みる。
対称性を考慮する
行と列や各向きの斜めといった対称性を利用することで、得られる結果がどうなるか確かめる。具体的には、1個のクイーンの位置を固定する。固定する位置もいくつか考えられるが、ここでは1行2列目にクイーンを配置するようにする。このために横磁場項hに予め設定しておく。予めhの1行2列目だけ-5(それ以外は0)としてから、QUBO行列を作成した。式(4-2)の場合で100回アニーリングを行なったところ、1種類の解のみ得られた。また実験の条件を変えることで、クイーンの位置を固定した場合でも異なる解が得られるだろう。
1行2列目にクイーンを固定した場合の解
このとき、目的関数のエネルギー分布は以下のようになった。固定しない場合と比べて、基底状態に達する割合が大きくなっていることが分かる。
クイーンの位置を固定した場合の目的関数のエネルギー分布
上記のように、いくつかのクイーンを予め配置した上で残りのクイーンの配置を決定する問題(N-queens Complesion Problem)も考えられている。セント・アンドルーズ大学のIan Gent教授は、彼の論文(“Complexity of n-Queens Completion” byIan Gent, et al.)の中で、この問題とN-クイーン問題の困難さについて述べている。
qbsolvを用いてより大きな問題を解く
D-Wave社が開発しているソルバーqbsolvといった、大きな問題の分割を行なうソルバーを用いることでより大きな問題に対処できる。現在、qbsolvはD-Wave Ocean SDK(github、ドキュメント)の一部として提供されている。
$N=12$において、目的関数とパラメータは上記の式(4-2)の場合とした。以下に得られた解の一部を示す。
qbsolvを用いた場合の12×12マスの解
応用例
ここでは、N-クイーン問題の応用例を取り上げる。IBMが開発している量子ゲート方式の量子コンピュータを用いたN-クイーン問題に関する論文(“A Novel Quantum N-Queens Solver Algorithm and its Simulation and Application to Satellite Communication Using IBM Quantum Experience” by Rounak Jha, et al.)では、$N=4$の場合におけるシミュレーションと人工衛星への応用が述べられている。
クイーンと人工衛星の反射器、チェス盤と人工衛星が周回する平面が対応し、情報をビームとしてやり取りが行われる。送信される情報の量と、反射器のために送信される地上面積を最大にすることを目的とする。2つのビームが同じ行や列、対角線に沿って伝送される場合、時間とともにランダムに変化する位相差を持つ時点で連続的に干渉する。それが信号波の重ね合わせにつながり、両方の反射器によって送られる情報が失われてしまう。N-クイーン問題の解のように反射器を配置することで、いずれのビームも同じ行、列または対角線に沿って情報を送信せず損失を抑えることができる。
まとめ
まとめと感想
N-クイーン問題の概要を紹介した後、異なる制約項の与え方に対して得られる解とエネルギーについて実験を行なった。制約項の与え方によって、エネルギー分布が異なり、基底状態の解にも違いがみられた。またアニーリング回数の変化や実験を行なうごとに、得られる解、つまりクイーンの配置が変わってくる。これは、ヒューリスティックな埋め込み、各アニーリングによると考えられる。
多くの問題において制約項の与え方はいくつか考えられ、どのような式の場合に望ましい解が多く得られるのか、その与え方によってどのような差異がみられるのかといった疑問を以前から感じていた。解くことができる問題の大きさは未いまだ小さいものの、この疑問に取り組む上での題材としてとても面白い問題であった。現在は量子コンピュータの黎明期であり、扱える問題の大きさや量子ビットのアーキテクチャによる制約を考慮して、問題に取り組むことが重要となる。本記事のように、実際にD-Waveマシンを用いて問題を解くことで、最適化問題のソルバーとしてD-Waveマシンを扱う上での知見を深めていきたい。
今後行いたいこと
- 得られた結果をさらに分析し、基本解、バリエーション解について調べる
- 各項のパラメータの最適な値を、効率的に探索できないかサーベイする、また実験を行う
- D-Waveマシンの次世代機が登場したら、同様の実験を行う
参考文献・サイト
- Wikipedia-エイトクイーン(日本語、英語)
- “A survey of known results and research areas for n-queens” by Jordan Bell, et al.
本記事の担当者
丸山尚貴