与えられたグラフを, 切断する辺の数を最小にしていくつかの部分グラフに分割する(最小カット問題) グラフ分割問題 をイジングスピングラス表現で定式化し, D-Wave 2Xにより解いた。グラフ分割問題 はKarpの21の組合せ最適化問題の1つとなっている。分割数が2の場合とそれ以上の数の場合では表現形式が異なることが興味深い。
文献情報
Hayato Ushijima-Mwesigwa, Christian F. A. Negre, Susan M. Mniszewski, “Graph Partitioning using Quantum Annealing on the D-Wave System”, arXiv:1705.03082 [quant-ph].
グラフ分割問題
本論文で扱う問題の定式化は, 分割数が2の場合とそれより大きい一般のKの場合でイジングスピングラス表現が少々異なる.
分割数が2の場合
最適化問題の定式化

分割数が2の場合, イジング表現(二値変数として+1か-1)で表現するのが自然である.
変数
$$s_i = \{ -1, 1 \}$$点iが-1,1でどちらのグループに所属しているかを示している.
目的関数

D-Waveマシン実装上の工夫
スレッショルドという手法で指定した値以下の数値は0として扱うと, 計算に必要なqubitsが減るのでD-Waveに実装しやすくなるメリットがある. しかし, 同時に精度も落ち, モジュラリティが0となりランダムカットにさえ優位差を持てないケースもある.
(モジュラリティ:点の次数を変えずにランダムに線をつなぎ合わせた時を比較対象にしてどれだけ優れた分割をしているかを示した値)
用いたデータセット
Random graph models, the Walshaw Archive, QMD molecule electronic structure graphsのグラフを用いてそれらのノードとリンクを入力データとした. またMETIS, KaHIPを既存のグラフ分割プログラムとして比較対象として使用した.
結果
sapi Python, qbsolvの二種類を使い, D-Wave systemでグラフ分割問題を解かせ, その結果をMETIS, KaHIPと比較した. 実際の数値データの一部を以下に載せる. (数字はグラフ分割の際に切った線の数で少ない方が優勢)

結果を見ていくと, グラフによって多少の有利不利はあれども, 二分割に関しては, 同等もしくは優勢という結果が得られた.

分割数がKの場合
最適化問題の定式化
変数
$$x_{ij} = \{ 0, 1 \}$$
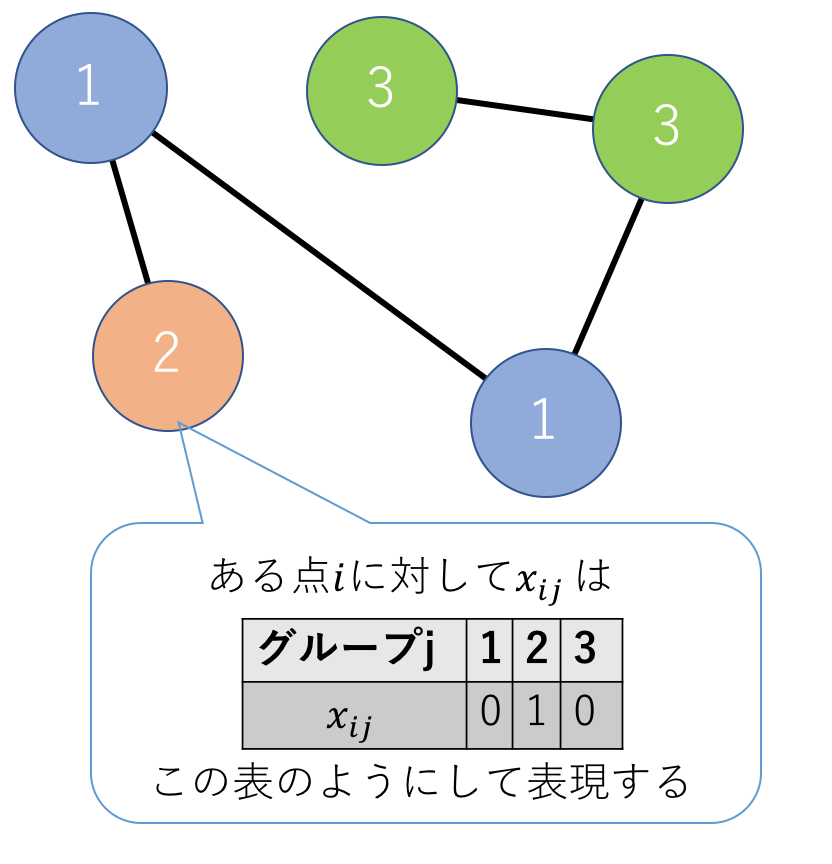
2より大きい一般のK部分グラフに分割する場合はQUBO表現(二値変数として1か0)で表すことが自然である. 点iがグループ$ j \in \{1,2,…,k\}$ に所属していたら1,そうでなければ0というように表現する.
目的関数

ここで第一項内にあるLという行列はラプラシアン行列である.
結果
二分割と同様の条件で行った実験の結果の一部を以下に載せる.

グラフによって既存の方法かqbsolvが良いのかが異なる. その理由としてqbsolvではルールから点の所属グループを一気に決めるのに対し, METISは凝集型階層的クラスタリングを使い, より相関が強い点を集めていく手法をとっているためグラフによって有利不利が生まれている. しかし, 基本的には既存の方法と同じかより高い質のグラフ分割がなされている.

本記事の担当者
金垣葵(編集: みやままさみち)