本記事で取り上げる論文では 迷路 における最短経路を求める問題をイジングスピングラスとして定式化し、D-Wave 2Xを用いて解いた結果を示している。補助ツールとして、問題を小問題に分割し、D-WaveマシンのキメラグラフにマップするQMASM(quantum macro assembler)を用いている。入出力やイジング模型へのマッピング、さらには 量子アニーリング にかかる時間のベンチマークや、そしてアニーリング時間による解の時間対精度などについても考察をしている。
文献情報
Scott Pakin, “Navigating a Maze using a Quantum Annealer”, Proceeding of PMES’17 Proceedings of the Second International Workshop on Post Moores Era Supercomputing, 30-36 (2017).
迷路の組合せ最適化問題としての定式化
迷路の定義と解の経路が満たすべき条件
本論文では、以下のような6×6のマスから構成される迷路を考える。任意のマスを(列, 行)で表すことにする。(下図では、例えば(A1)は最も左上のマスであり、入口と出口が(B6), (F1)である。)
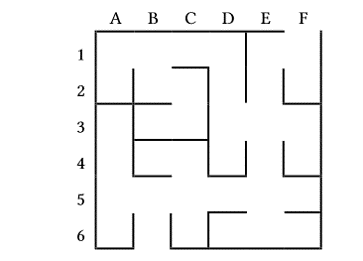
解となる最短経路は以下の3つの条件を満たしている必要がある。
①. 入口と出口は必ずどちらも含まれる。
②. 壁を通り抜けることはできない。
③. マスに入ったら必ず出なくてはいけない。また、複数回マスに入ることはできない。
迷路問題のイジング表現としての定式化
変数:$\sigma \in \{ +1, -1 \}$ (経路に含まれるなら+1, そうでなければ-1)
まず、上の図の右上に注目する。

これは、(E1)と(F1)のマスに着目した図である。$\sigma_{\mathrm{i}}$は迷路の入り口を表す変数であり、それ以外の$\sigma$は各マスの中の各方向の経路を表す変数である。$\sigma$はどちらも±1のどちらかの値をとり、最短路に含まれる$\sigma$は+1を、含まれない$\sigma$は-1をとるものとする。
この部分を例題の部分的な具体例としたうえで以下で上の3条件を定式化する。
条件① 入口と出口は必ずどちらも含まれる
入口である$\sigma_{\mathrm{i}}$に着目する。すると、入口のハミルトニアンは以下のようになる。
$$ \begin{aligned} \mathcal{H}_{\mathrm{ingress}}=h_{\mathrm{N}} \sigma_{\mathrm{N}} + h_{\mathrm{i}} \sigma_{\mathrm{i}} + J_{\mathrm{N, i}} \sigma_{\mathrm{N}} \sigma_{\mathrm{i}} = – \sigma_{\mathrm{i}} – \sigma_{\mathrm{N}}\sigma_{\mathrm{i}} \end{aligned} $$ここで、$h_N=0, h_i=-1$,そして$J_N, i=-1$としている。これにより、どちらの$\sigma$も+1の時にこのハミルトニアンは最小値をとる。ゆえにこの式は条件を満たしている。これと同様にして、(B6)のマスにある出口も以下のようなハミルトニアンで表すことができる。
$$ \mathcal{H}_{\mathrm{egress}} = h_{\mathrm{S}} \sigma_{\mathrm{S}} + h_{\mathrm{e}} \sigma_{\mathrm{e}} + J_{\mathrm{S, e}} \sigma_{\mathrm{S}} \sigma_{\mathrm{e}} = \sigma_{\mathrm{e}} – \sigma_{\mathrm{S}}\sigma_{\mathrm{e}} $$条件② 壁を通り抜けることはできない
(E1)のマスの$\sigma_{\mathrm{W}}$を例とする。$\sigma_{\mathrm{W}}$方向には壁があるため、その方向は最短路に含まれることはない。ゆえに、$\sigma_{\mathrm{W}}=-1$となるはずである。また、$\sigma_{\mathrm{W}}$方向の壁を表す変数を$\sigma_{\mathrm{wall}}$とすると、これは常に-1である。ゆえに①の時とは異なり、$h_{\mathrm{W}}=0, h_{\mathrm{wall}} =1$,そして$J_{\mathrm{W, wall}}=-1$とすると、(E1)の$\sigma_{\mathrm{W}}$方向の壁に関するハミルトニアンは
$$ \begin{aligned} \mathcal{H}_{\mathrm{wall}} = h_{\mathrm{W}} \sigma_{\mathrm{W}} + h_{\mathrm{wall}} \sigma_{\mathrm{wall}} + J_{\mathrm{W, wall}} \sigma_{\mathrm{W}} \sigma_{\mathrm{wall}} = \sigma_{\mathrm{wall}} – \sigma_{\mathrm{W}}\sigma_{\mathrm{wall}} \end{aligned} $$となる。
条件③ マスに入ったら必ず出なくてはいけない。また、複数回マスに入ることはできない
まず、条件の視覚的な説明をする。③の条件を満たすのは以下の3通りである。

左の図は経路としてマスが使われない場合である。また、真ん中と右の図は、一回マスに入りそのままマスを出て戻ってきていない場合である。このどちらの場合も最短路に含むことができる。
次に、③の条件を満たさない場合である。それは以下の3通りである。

左の図はマスに入ったまま出ない場合である。また、真ん中と右の図は、複数回マスに入ってしまっている。これらは最短路に含むことはできないので、このようにならないようにハミルトニアンを定義する必要がある。
$$ \begin{aligned} \mathcal{H}_{\mathrm{room}} &= \frac{1}{2} (\sigma_{\mathrm{N}} + \sigma_{\mathrm{E}} + \sigma_{\mathrm{W}} + \sigma_{\mathrm{S}}) + \sigma_{\mathrm{a}} \\ &\qquad + \frac{1}{4} (\sigma_{\mathrm{N}} \sigma_{\mathrm{E}} + \sigma_{\mathrm{N}} \sigma_{\mathrm{W}} + \sigma_{\mathrm{N}} \sigma_{\mathrm{S}} + \sigma_{\mathrm{E}} \sigma_{\mathrm{W}} + \sigma_{\mathrm{E}} \sigma_{\mathrm{S}} + \sigma_{\mathrm{W}} \sigma_{\mathrm{S}}) \\ &\qquad + \frac{1}{2} (\sigma_{\mathrm{N}} \sigma_{\mathrm{a}} + \sigma_{\mathrm{E}} \sigma_{\mathrm{a}} + \sigma_{\mathrm{W}} \sigma_{\mathrm{a}} + \sigma_{\mathrm{S}} \sigma_{\mathrm{a}}) \end{aligned} $$①、②のような形のハミルトニアンで表したかったのだが、その形ではうまく表せないためhとJを適切に選択したうえで補助変数$\sigma_{\mathrm{a}}$を用いている。これは$\sigma_{\mathrm{N}}$から$\sigma_{\mathrm{W}}$がすべて負の時に+1を取り、それ以外の時は-1を取る。
$$ \mathcal{H}_{\mathrm{E1}} = \mathcal{H}_{\mathrm{room}} + \mathcal{H}_{\mathrm{wall}}(\mathrm{N}) + \mathcal{H}_{\mathrm{wall}}(\mathrm{W}) $$ $$ \mathcal{H}_{\mathrm{F1}} = \mathcal{H}_{\mathrm{room}} + \mathcal{H}_{\mathrm{wall}}(\mathrm{E}) + \mathcal{\mathrm{H}}_{\mathrm{ingress}}(\mathrm{N}) $$となる。しかし、マス(E1)とマス(F1)の二つのマスの全体のハミルトニアンを考えるときは、注意が必要である。マス(E1)とマス(F1)の壁で隔てられていない隣り合う経路はどちらも+1になる必要がある。よってそれを踏まえると、マス(E1)とマス(F1)を全体のハミルトニアンは以下のようになる。
$$ \mathcal{H}_{\mathrm{E1, F1}} = \mathcal{H}_{\mathrm{E1}} + \mathcal{H}_{\mathrm{F1}} – \sigma_{\mathrm{E}}^{(\mathrm{E1})} \sigma_{\mathrm{W}}^{(\mathrm{F1})} $$これを各マスについて考え、この操作を行うことで例題の迷路の全体のハミルトニアンを求めることができる。
実行結果
QMASMを用いて、ハミルトニアンに現れる219個の変数をキメラグラフにマッピングしたところ、60回の試行で580.25±39.71個のqubitで表現することができた。
また、20μsでの量子アニーリングを10000回行うといった試行を行い、各機能のベンチマークを行った。30回繰り返すことにより以下の表が得られた。数値は平均値と標準偏差で表されている。

20μsでのアニーリングを10000回行うといった試行は平均しておよそ20.3秒もかかっており、6×6の迷路で得られた結果としては些か不満足な結果となった。しかしながら、実際にQPUで処理にかかっている時間は約1.9秒であった。また、QMASMにより場合によってはかなりの高速化が期待できており、これは最大のボトルネックであった、D-Wave’s minor embedderの処理を簡略にしているためである。更に、上の表からわかる通りSAPI postprocessingもかなりの処理時間を要しており、古典的なpostprocessingがボトルネックになってしまっていることが判明した。
次に、アニーリング時間による、試行回数に対する解の精度ないしは時間対精度の変化を、postprocessing無しの場合と有りの場合で比較した。1000000回のアニーリングをして得られた結果は以下のようである。

postprocessing無しの場合は、アニーリング時間20μsの時に優れた時間対精度が得られた。一方、アニーリング時間2000μsの時に試行回数に対する解の精度が最も優れるという結果になった。postprocessing有りの時は、その有用性がどのアニーリング時間の場合でも顕著に得られた。特に、アニーリング時間5μsの時は、時間対精度が非常に優れた結果となった。これは、古典的なpostprocessingによって極小値ではなく最小値が得られるようにしているためである。
本記事の作成者
今井柊平(編集:みやままさみち)