文献情報
タイトル: Traffic Flow Optimization Using a Quantum Annealer
著者: Florian Neukart, Gabriele Compostella, Christian Seidel, David von Dollen, Sheir Yarkoni and Bob Parney
書誌情報: https://doi.org/10.3389/fict.2017.00029
概要
D-Wave Systemsによって開発が行われている量子アニーリングマシンは、組合せ最適化を高速に解くソルバーとして活発な分析が行われています。本論文では、渋滞解消を目的とした自動車の移動経路割当を組合せ最適化問題として定式化します。連続的な経路割当を実現するには最適化の高速性が求められるが、北京首都国際空港近辺における過去のドライブデータを用いてシミュレーションを行った結果、量子アニーリングは有効的な手法の一つであることを示しています。
目的
本論文では、各車両の出発地から目的地までの移動時間を最小化することを目的としています。
ある一本の道路に要する移動時間は、その道路上の車両台数に比例するとみなすことができるので、
今回は車両混雑を分散化する最適化問題として定式化します。
手法
本論文では、古典コンピュータによって各車両に代替経路を定め、量子アニーリングによって交通渋滞を軽減する経路を選ぶという方法が取られています。このような車両の経路の再分配の問題は組合せ最適化問題に分類され、台数が増えると古典コンピュータでは実用的な時間で解くことが難しい場合があります。一方、量子アニーリングは組合せ最適化問題を高速に解くことができると将来的に期待されています。したがって、本論文では解を求める手段として量子アニーリングを用います。
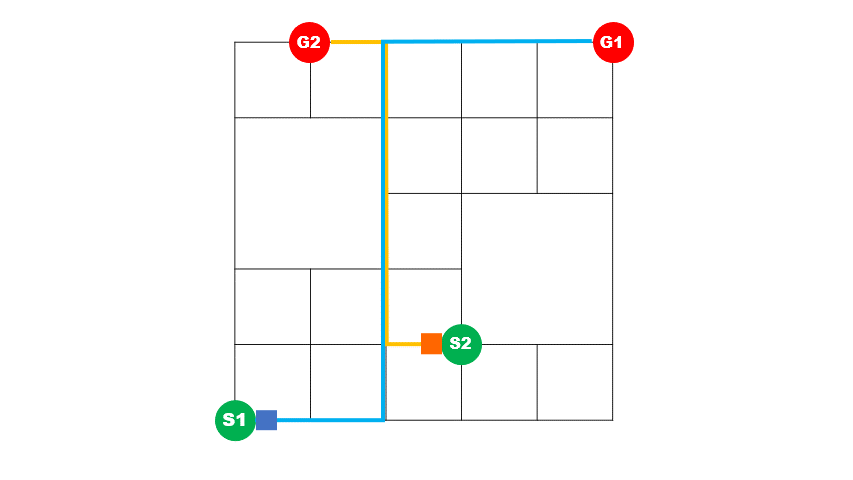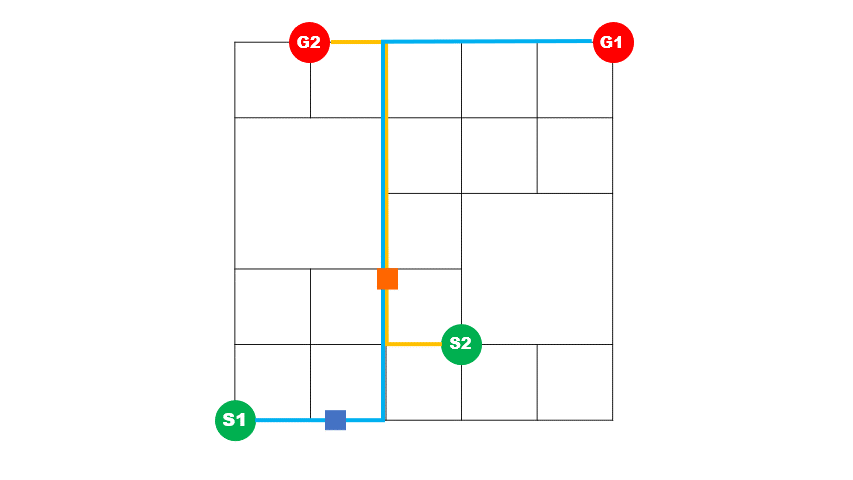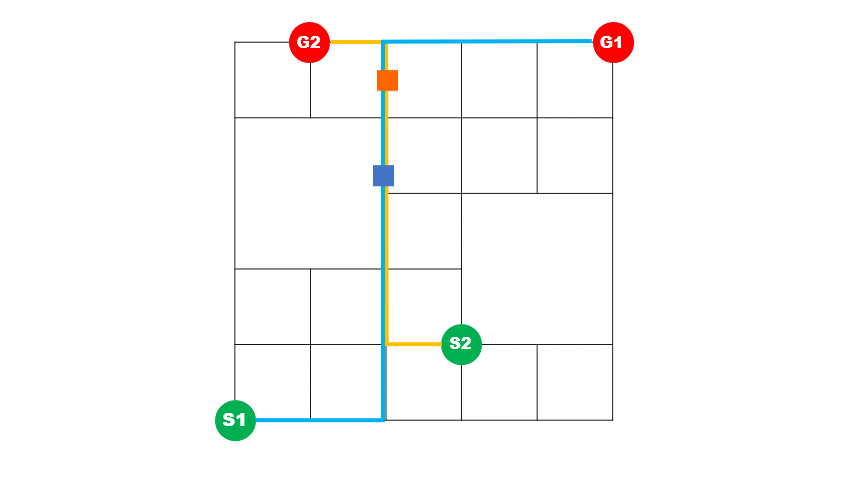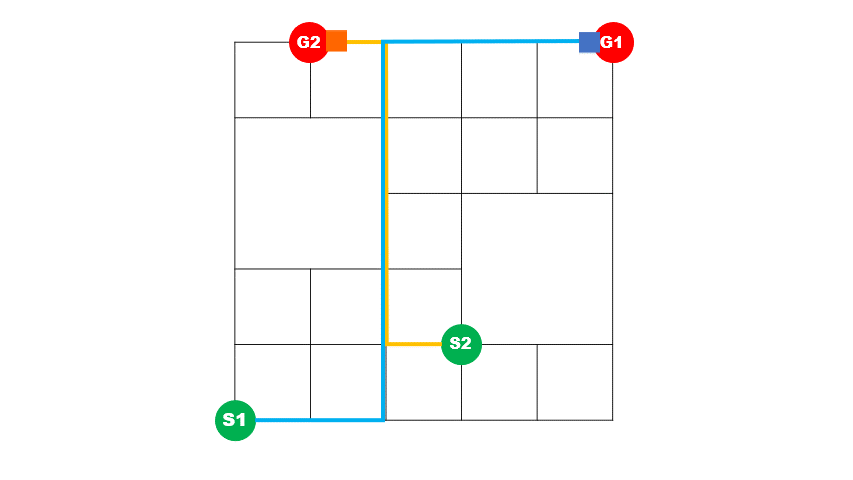
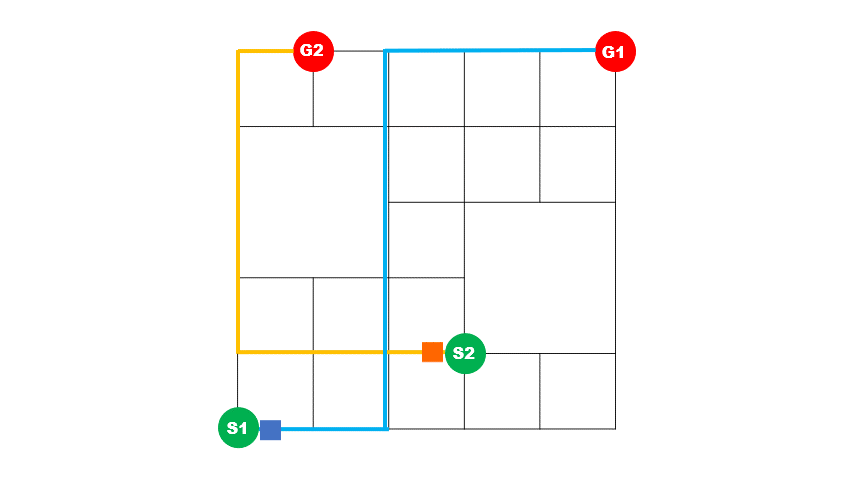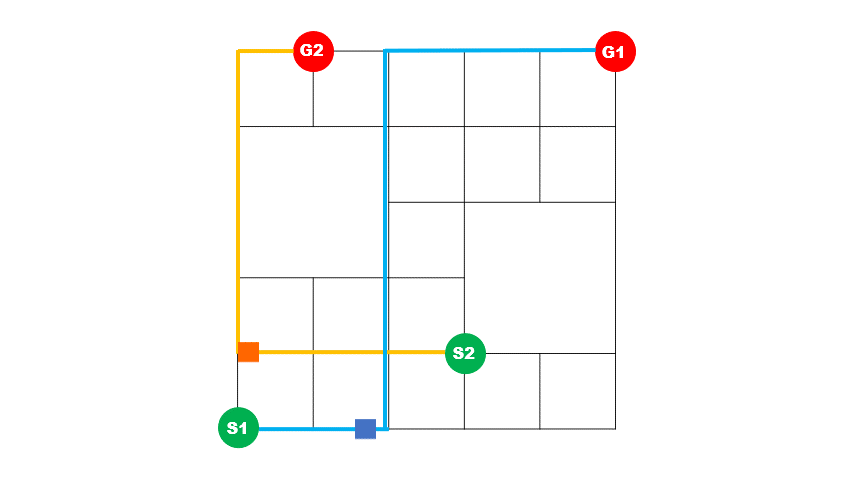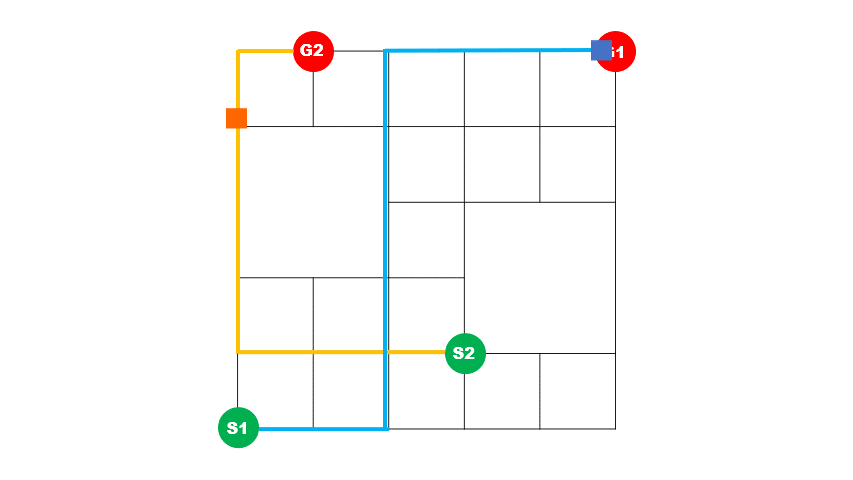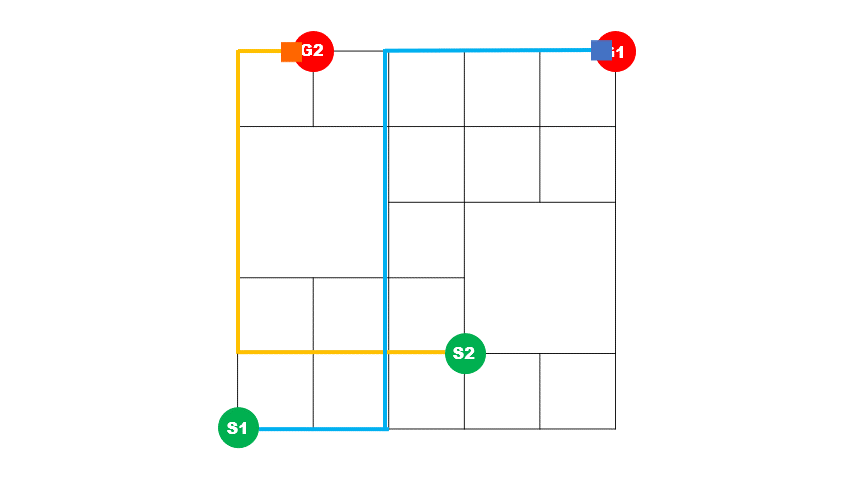
上)最適化前イメージ 2台の車の経路が重なっている区間が多く、青い車が途中で詰まっていることが分かります。
下)最適化後イメージ 2台の車の経路が重なっている区間が短く、青い車が詰まることなく目的地に到着していることが分かります。
具体的には以下のプロセスを混雑が解消するまで繰り返します。
- 車両のGPSデータを用意し、それぞれの目的地、出発地および経路を取得します。
- 目的地から出発地までの全ての経路を求め、このうち2つの経路を選びます。
(ただし、なるべく各候補経路が類似しないように選びます。) - 量子アニーリングによって、全ての車両について2で選んだ3つの経路から、各車の混雑を軽減するような経路を選びます。
下図)1台の車に対する3つの経路のイメージ
各経路において互いに共有される道路が少なく、類似していないことが分かります。
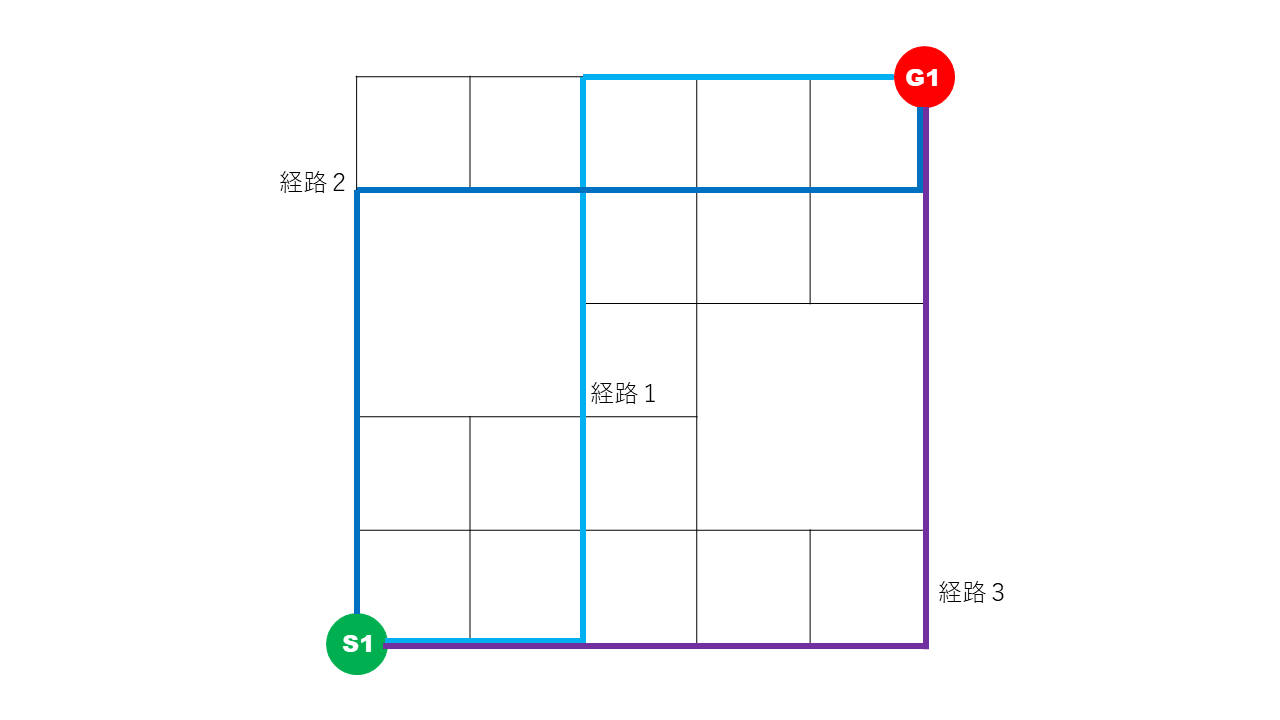
次に混雑を軽減するように候補経路から実際の移動経路を選ぶ問題を定式化します。
ここで、各車両について、$ i = 1, 2, \dots, n $ と番号を振り分け、各車両に割り当てられた3つの経路について$j = 1, 2, 3$ と番号を振り分けます。そして、$ q_{ij} $ を車 $ i $ が与えられた経路 $ j ~ (=1, 2, 3) $ のうち、どの経路を選択したのかを表す二値変数とします。
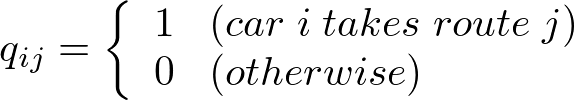
すると、最小化するコスト関数は次のように定義できます。
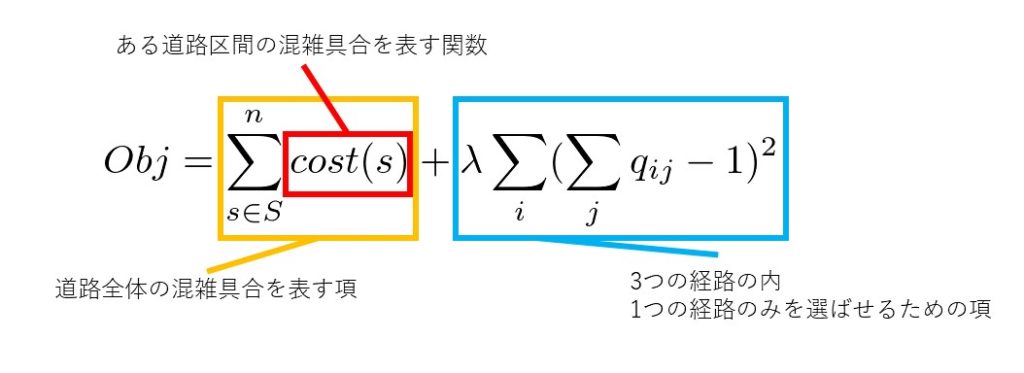
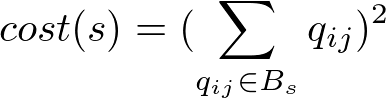
Objの値を最小に近づけた時、それぞれの車iに対して選ばれた経路jが、混雑を解消する経路となります。
右辺第一項は、全ての道路区間における車の経路の重なり度合いを表す目的関数です。sはある道路区間、Sはすべての道路区間の集合を表わします。またBsは道路区間sを通るような変数の集合を表します。したがって、cost(s)は道路区間sの混雑度合いを表わす関数となり、右辺第一項は全ての道路区間の混雑度合いを足し合わせた項ということとなります。
右辺第二項は、任意の車両について、その3つの経路の内、ただ一つの経路を選択するようにするための制約条件です。ただ一つの経路を選んだ場合のみ、Σj cost (s)の値は0となりますが、そうでない場合は0より大きい値を取ります。λは目的関数に対する制約項の強さを表し、十分に大きい値に設定する必要があります。今回は、λをcost (s)の中に表れる車iの最大値としています。
結果
本論文における実験は、北京首都国際空港近辺をモデルとして行われました。1週間に渡って記録されたT-Driveの10,357台のタクシーの経路データのうち、都心と空港を往来する418台のデータを抽出しました。地図データについては、OSMnxを用いて北京の道路ネットワークを抽出しました。
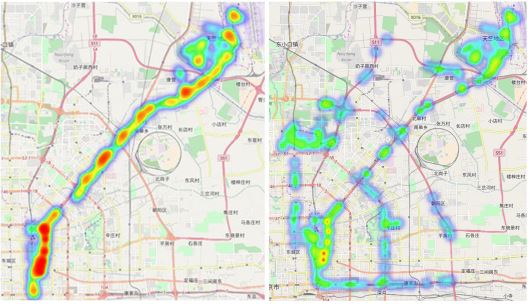
上図の左側の画像が最適化する前の場合で、右側の画像が量子アニーリングによって最適化した場合です。赤は車両が集中している箇所、青は車両が少ない箇所を示しています。最適化することによって、混雑が軽減されていることが分かります。
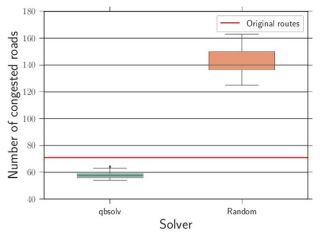
また、本論文では、最適化前 (元データ) と最適化後、さらにランダムに道を選んだ場合の道路の混雑度を比較しています (上図)。最適化を行った場合の混雑している道路の数は、最適化前の場合よりも少ないことが分かります。また、ランダムに経路を選んだ場合の混雑している道路の数は、最適化前の場合よりも多いことが分かります。
編集者あとがき
本論文では、量子アニーリングが渋滞の軽減に有効であることは分かりました。しかしながら、どれほどの頻度で計算を行ったかについて詳しく言及されておらず、その効率の良さについては分かりませんでした。また、当初の目的は、出発地と目的地の移動時間を最小化することでしたが、途中から目的が道の混雑を軽減することになっていました。道の混雑を軽減することによって、一見移動時間も短縮されるように思われますが、回り道をした結果、より時間がかかってしまったということもあり得るのではないかと考えました。
実験結果については、最適化前、最適化後、ランダムの三種類の経路の選び方によって比較していました。今回の実験はタクシーのデータを用いていますが、量子アニーリングによって、北京の都市に慣れたタクシードライバーよりも効率的な経路選択が行われていました。このことから、明文化が難しい経験についても、技術・技能が無い段階から最適解を選ぶことが可能なことが分かります。このような経路最適化と、信号最適化が相互に影響し合うことによって、交通インフラがさらに効率の良いものとなるのではないかと考えました。
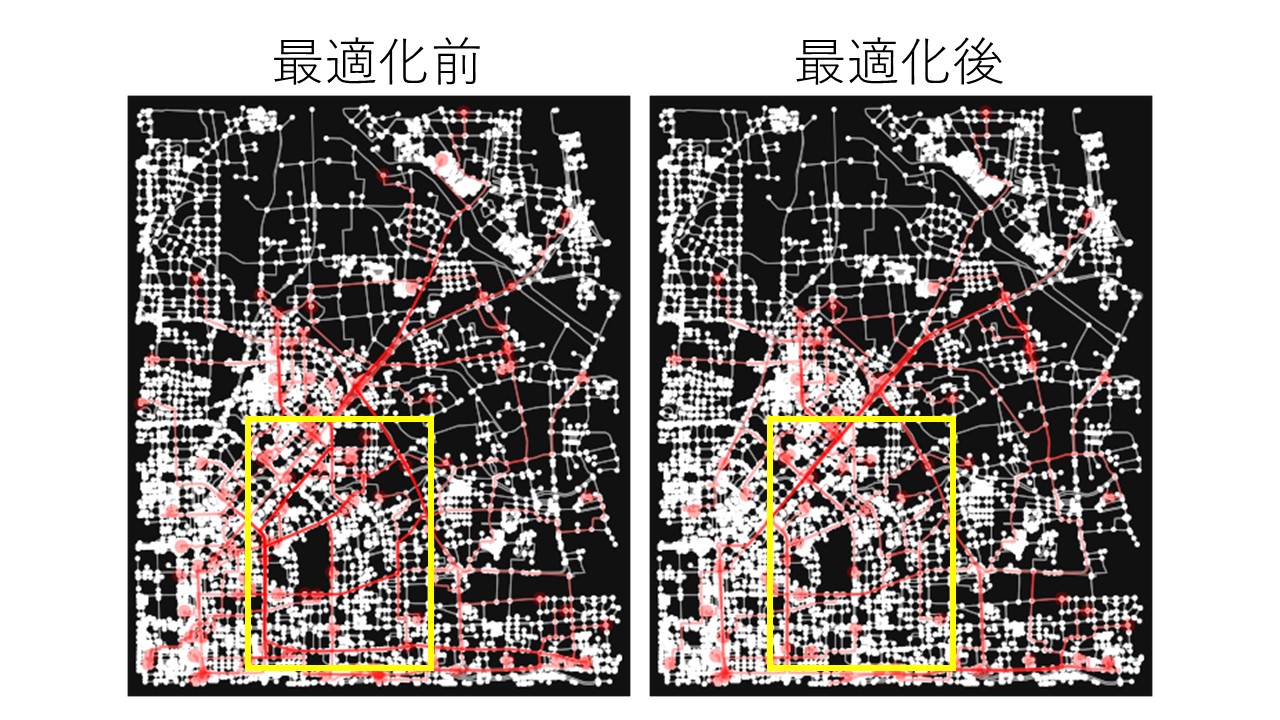
また、私自身も本論文と同じ範囲でシミュレーションを行った結果が以下の図になります。
左の図が最適化する前、右の図が最適化した後の道の混雑具合を表した図になります。赤色が濃くなればなるほど混雑していることを示しています。論文とは方法が少し異なり、ランダムに選んだ50台の車の経路を最適化した結果ですが、このようなシミュレーションでも、量子アニーリングによる最適化によって、特に図の黄色の枠で囲まれた地域の道の混雑が軽減されることが分かります。
本記事の担当者
岡田朋久 (メンタリング:丸山尚貴、羽場廉一郎)