文献情報
タイトル: A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer
著者: Sebastian Feld, Chrisoph Roch, Thomas Gabor, Christian Seidel, Florian Neukart, Isabella Galter, Wolfgang Mauerer, and Claudia Linnhoff-Popien
書誌情報: https://doi.org/10.3389/fict.2019.00013
概要
CVRP (容量制約有りの配送計画問題)は、積載容量に制約のある車両で効率よく荷物を配送することを目的とした問題です。CVRPは、NP困難な問題であり、顧客の数が増えると組合せも爆発的に増加するため、全探索を用いて最適解を求めるには限界があります。そのため、古典的な手法では近似解を求めるのが主流です。この論文では、CVRPを小さな問題に分割し、量子アニーリングマシンと古典コンピュータの両方を用いたハイブリッドな手法を用いて解きます。そして、解の質や計算時間について古典的な手法との比較、および量子アニーリングマシン(D-Wave 2000Q)の性能の評価を行っています。
なぜCVRPを量子アニーリングマシンで解くのか
量子アニーリングは量子力学的な効果により古典コンピュータよりも高速に最適解を求めることができると期待されています。しかし、CVRPはこれまで量子アニーリングマシンの有効性が未知であった問題でした。そこで、本論文ではD-Waveの量子アニーリングマシンを用いてCVRPを解いてみることにより、解の質や計算時間について利点があるかを明らかにしています。
CVRPを解く上での課題
課題①:量子ビットの数に制限がある。
量子アニーリングマシンで問題を解くためにはQUBO問題に落とし込む必要があります。しかし、CVRPのようなサイズの大きい問題を扱う場合、実機の量子ビットの数に制限があるためそのままQUBO問題に落とし込むことはできません。
課題①の解決方法
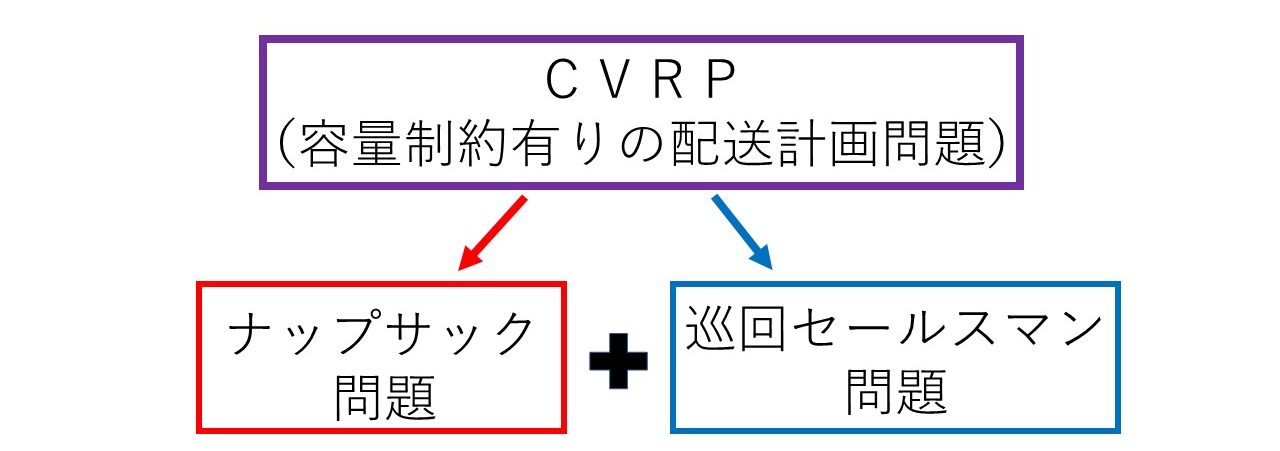
CVRPは次の2つの問題に分割して解を求めるヒューリスティックアルゴリズムが知られています。
ナップサック問題と巡回セールスマン問題です。
ナップサック問題は、容量の決まったナップサックになるべく価値が高くなるよう荷物を詰めることを考える問題です。今回の場合、容量制限付きの車がナップサックにあたります。巡回セールスマン問題は、セールスマンが都市を巡る最短経路を考える問題です。本論文の提案手法では、まずナップサック問題を解くことで、各車両の積荷の選定(クラスタリング)を行います。そして、各車両に関して巡回セールスマン問題を解くことで、最短の移動経路を求めます。
本記事では、ナップサック問題をクラスタリング、巡回セールスマン問題をルーティングと表現します。
このように大きな問題 (CVRP) を小さな問題 (ナップサック問題と巡回セールスマン問題) に分割することによって量子アニーリングマシンでCVRPを解くことを可能にしています。
課題②:量子アニーリングマシンのみで解くことが難しい。
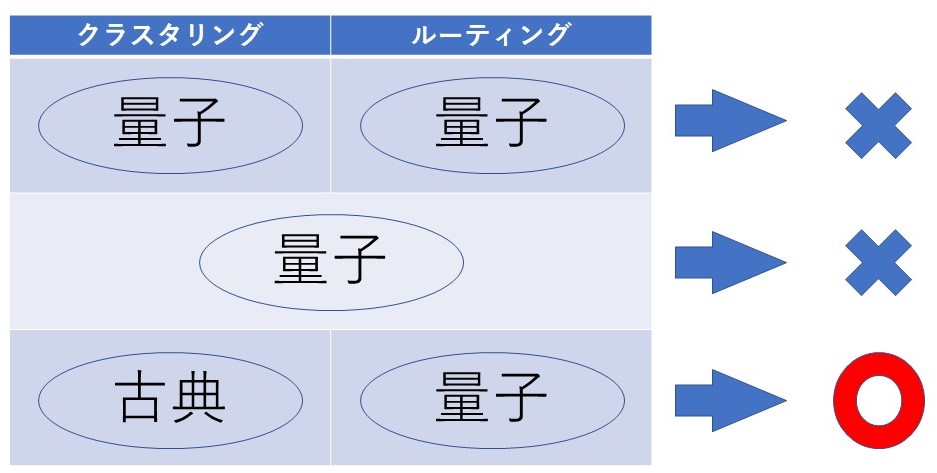
この論文では、まず量子アニーリングマシンのみで問題を解くことを考えます。しかし、2つの問題を分割して解く際には、クラスタリングの部分で問題が生じます。また同時に解こうとする際には最適化に関する項が干渉してしまいます。これらのことから、CVRPを量子アニーリングマシンのみで解くことは難しいです。(詳細については論文参照)
課題②の解決方法
量子アニーリングマシンと古典コンピュータを用いたハイブリッドな手法を用います。具体的には、前半のクラスタリングは古典コンピュータで、後半のルーティングは量子アニーリングマシンで解きます。
具体的な方法
クラスタリング(ナップサック問題)
まず、前半のクラスタリングは2つの段階に分かれています。①クラスターの生成と②クラスターの改善です。
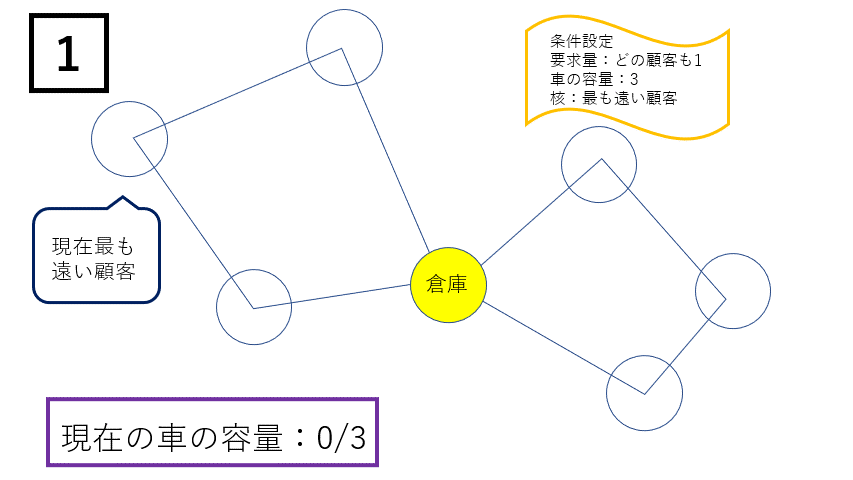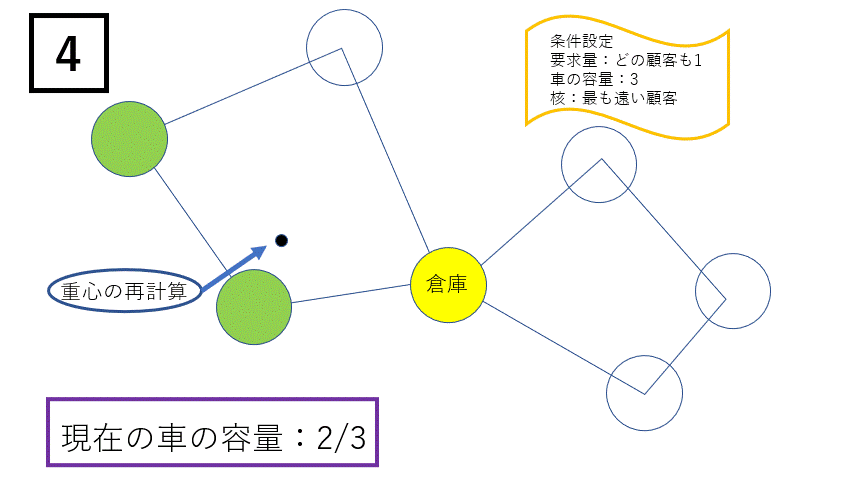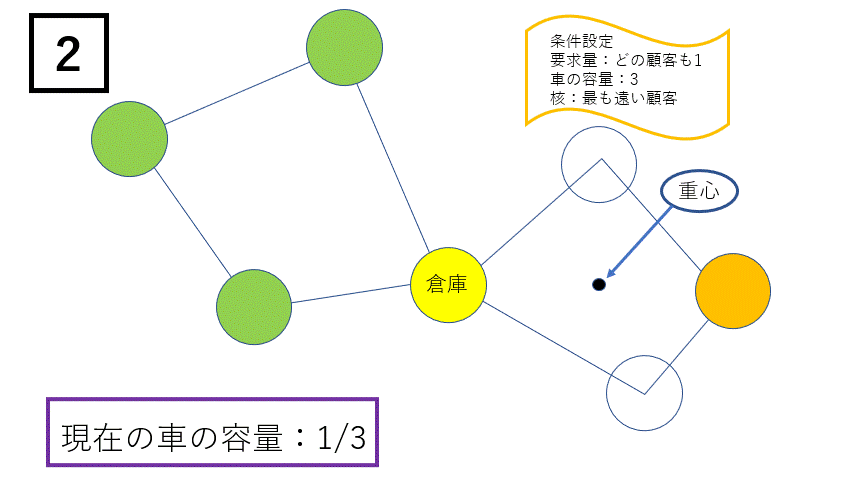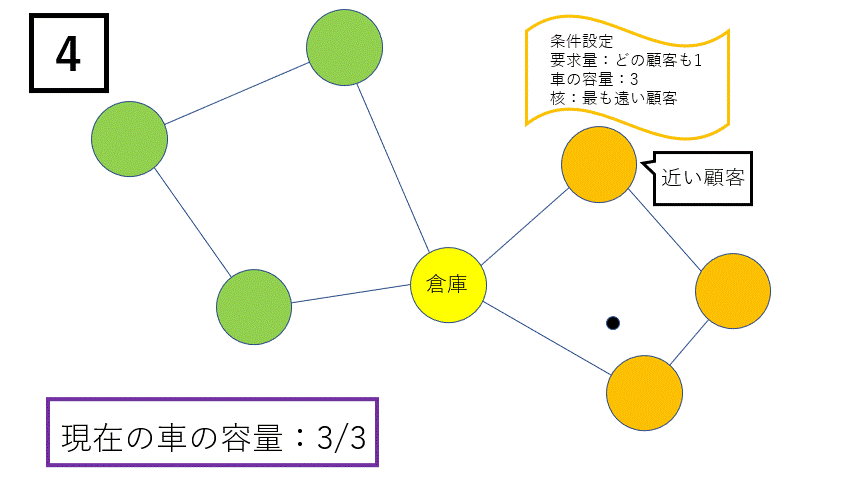
①クラスターの生成は以下の手順によって行われます。
- クラスターを生成する際に核となる顧客を決めます。今回は最も倉庫から遠い顧客、または最も荷物の要求量が多い顧客を選んでいます。
- 核となる顧客と倉庫の重心を求めます。
- その重心に最も近い顧客を新たにクラスターに加えます。この際、クラスター内の総要求量が車の容量を超えないようにします。
- 以下、上記の操作を繰り返します。もし車の容量を超える場合は新たな核となる顧客を決め、新しいクラスターを生成し、全ての顧客をクラスターに割り振ります。
次に、②クラスターの改善は以下のように行われます。
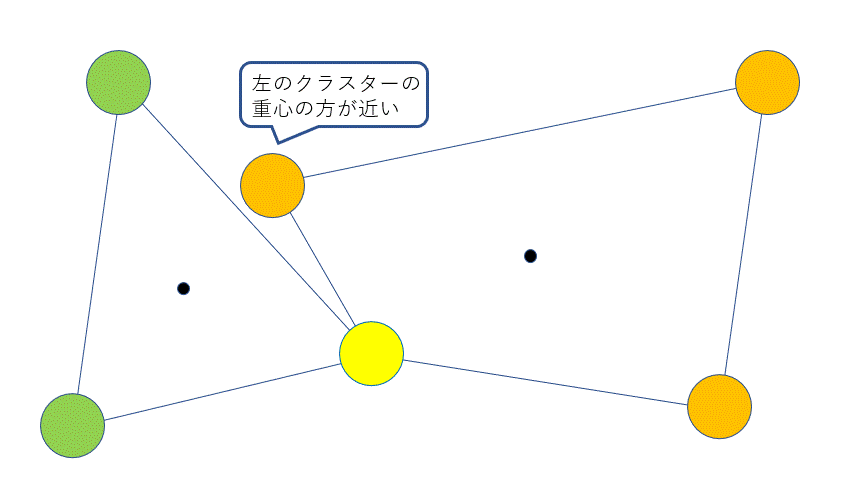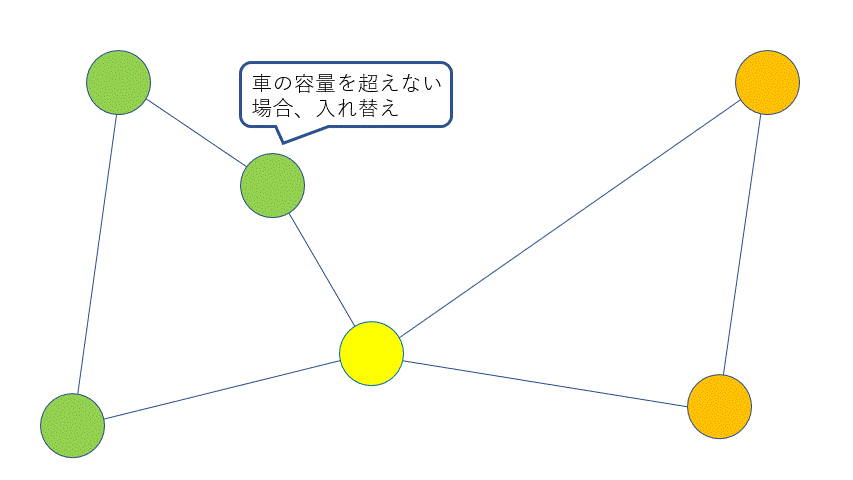
全ての顧客について、他のクラスターに移すことを考えます。もし、今いるクラスターの重心よりも他のクラスターの重心の方が近ければ、他のクラスターに移します。ただし、車の容量を超える場合はこの操作を行うことはできません。
以上を、クラスターに変化がなくなる、またはある位置に対して試行回数を決めておき、それに達するまで繰り返します。
ルーティング(巡回セールスマン問題)
次に後半のルーティングは以下のように定式化されています。
$$H=H_A+H_B$$
具体的な式は以下の通りです。
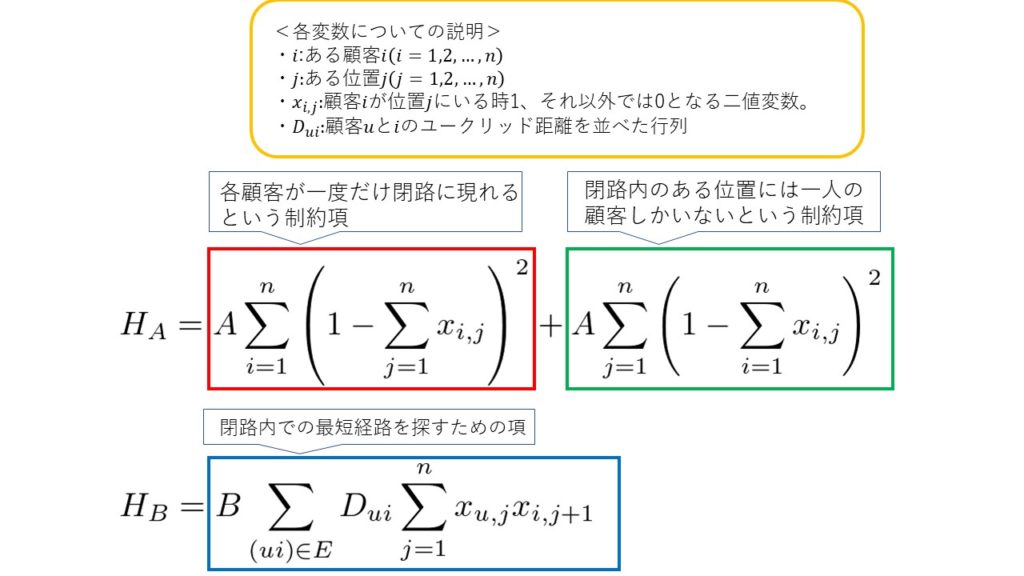
今回の実験の場合、各クラスターの頂点を一度だけ通る閉路を考えるため、ハミルトン閉路と考えることができます。それを定式化したものが$H_A$です。また、ハミルトン閉路内での最短経路を見つけるのが$H_B$です。
各項にかかっている係数について、$A$は制約項の強さを、$B$は目的関数の重みを決める役割を持ちます。今回の実験では、$A$が顧客数$n$と行列$D_{ui}$の最大値の積、$B$が1に設定されています。
結果
ルーティングはQUBO問題として、$n^2$個の変数を用います($n$は顧客の数)。
これらの変数同士の結合が、D-Wave 2000Qのハードウェアよりも密であるため、元の問題の構造をD-Waveのハードウェアで許容される問題構造 (キメラグラフ) に合わせることは困難です。そのため今回はD-Waveが提供しているマイナー埋め込みのヒューリスティックアルゴリズムを用います。
また、問題のサイズが大きいため、それを分割するためにQBSolvというツールを用います。これは、QUBOをより小さなsubQUBOに分割し、独立に解くツールです。分割はより良い解が見つかる限り繰り返されます。この回数はnum_repeatsによって制限されます。
また、QBSolvは分割して解くだけではなく、タブーサーチを用いて局所解を求める機能もついています。QBSolvは既存のコンピュータを使う場合でも、実機の量子アニーリングマシンを用いて解く場合にも使うことができます。今回は、既存のコンピュータを使う場合をローカル、実機の量子アニーリングマシンを用いて解く場合をリモートと表現します。
アニーリングの実行時間は20µsに設定されています。
ルーティングの評価
この実験では異なるサイズのルーティングのデータセットを対象としています。アニーリングの回数は100回です。また、num_repeatsは250に設定しています。
結果は、問題の名前(都市名、データの大きさ)、データの大きさ、BKS(最も良いと知られている解)、最良解(100回実行した際の最も良かった解)、各解とBKSの平均偏差の順に示されています。
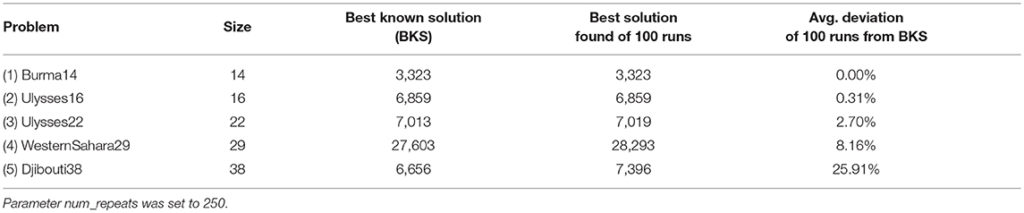
(1)(2)のようなサイズの小さい問題については、BKSとほとんど同じ解が求められ、各解の平均偏差も小さいことがわかります。しかし、(3)(4)(5)と問題が大きくなるにつれて、BKSよりも悪い解となり、偏差も増大しています。
また、この実験ではnum_repeatsを変更しての実験も行われています。結果は以下の通りです。今回は10回の試行です。いずれのデータセットについてもnum_repeatsが増加するにつれて、各解とBKSとの偏差が減少していることが読み取れます(i.e. 良い解が得られている)。
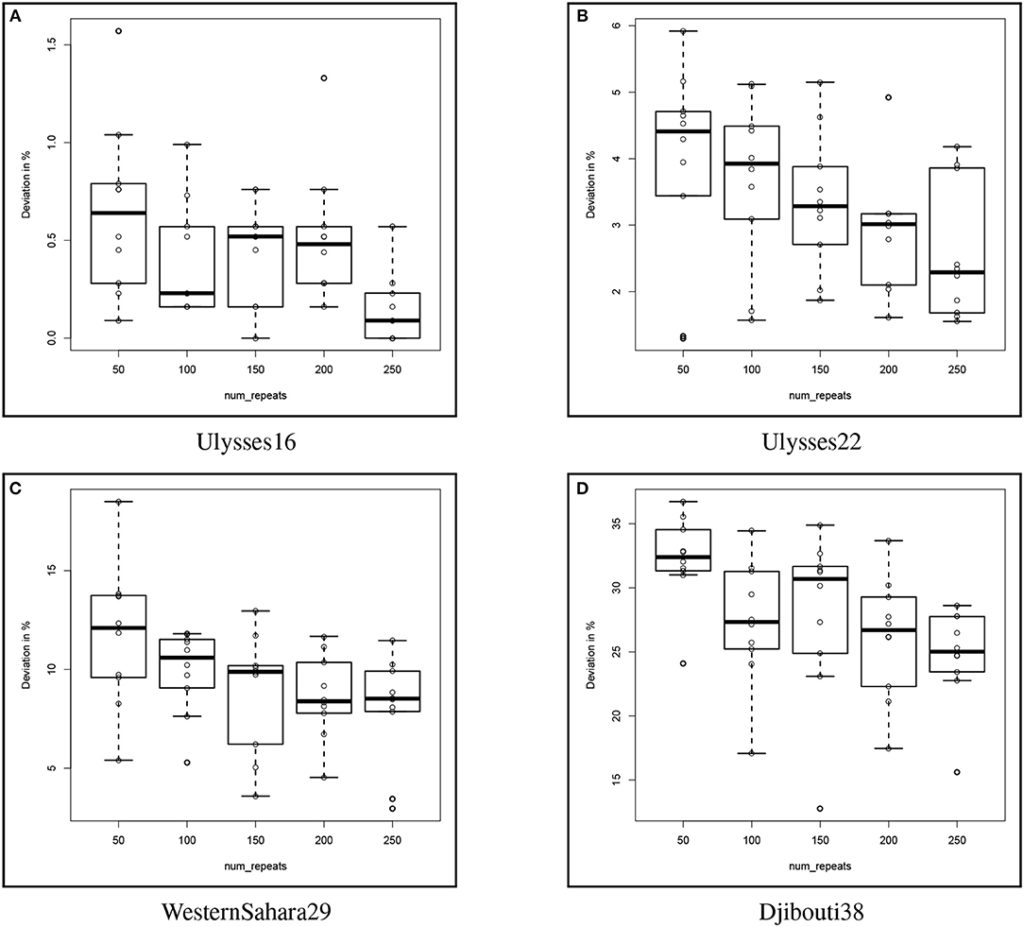
CVRPの解の質の評価
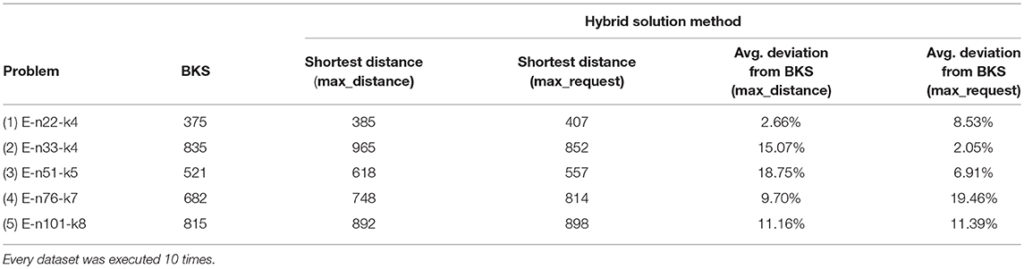
この実験では、はじめにクラスタリングを行う際のクラスターの核となる顧客の決め方(最も倉庫から遠い顧客、または最も荷物の要求量が多い顧客)の違いが解に及ぼす影響を調べています。結果はデータセットの名前(E-顧客の数-車の数)、BKS、2つの決め方における最も良かった解、2つの決め方における偏差の順に並んでいます。
結果を見ても、核となる顧客の決め方としてどちらが良いと具体的に言うことはできません。
続いて、7つのCMTデータセット(CMT1~5,11,12)を用いて、Clarke-Wrightの手法、Fisher-Jaikumarの手法、Christofides et al.の手法、Sweepアルゴリズムの4つの手法の性能と比較を行っています。結果はデータのサイズ、BKS、各手法における最良解と偏差の順に並んでいます。また、ハイブリッド手法においてaは距離が最大、bは要求量が最大のものを核となる顧客として選択した場合の解となっています。
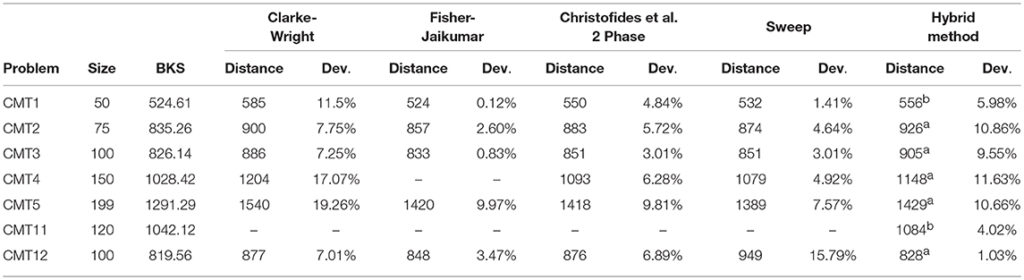
CMT1~5については、ハイブリッド手法は一つ目のClarke-Wrightの手法には劣らない性能であり、上回っている部分もあることがわかります。しかし、その他の手法よりは劣っています。CMT11,12は、顧客が地理的にまとまっているため、クラスタリングとしては比較的に容易であるデータセットです。表から読み取れる通り、ハイブリッド手法は他の手法と比較しても良い結果です。したがって、クラスタリングの性能が良い場合、ルーティングの性能も、他の手法より優れていることがわかります。
CVRPの計算時間の評価
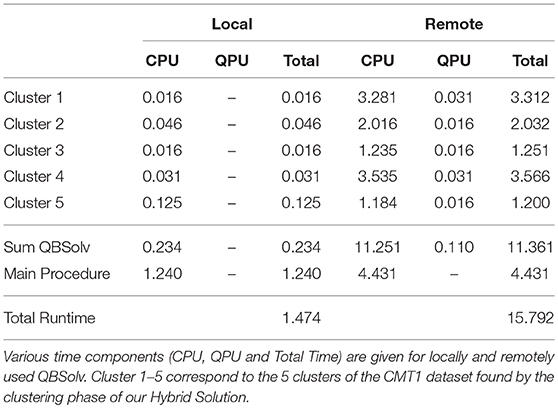
2つ目の実験で用いたCMT1のデータセットにおけるルーティングでの計算時間をローカルで解いた場合とリモートで解いた場合の計算結果を比較しています。ローカルの場合はCPUのみでルーティングを解いていますが、リモートの場合はCPUでQUBOの分割を行い、量子アニーリングマシンで分割されたsubQUBOを解いています。得られた解はローカルでは557、リモートでは556という結果であり、解の質はほぼ同等です。
表から、QUBO問題を解く時間についてはリモートの方が優れていることがわかります。しかし、ローカルと比べて、キメラグラフへの埋め込みや、インターネットの遅延、マシンの待機列によって合計の実行時間が長くなっています。そのため、トータルの時間で見ると、現状ではローカルで解く方が優れていると言えます。
結論
今回の実験では、サイズが大きい問題についてはBKSにたどり着くことができず、またローカルで解いた方が合計の実行時間が短かったため、解の質や計算時間について明確な利点は発見されませんでした。
しかし、地理的に顧客がまとまった現実的なデータについては、ハイブリッド手法によるCVRPの分割手法は他の近似解法と比べても良い結果であったことから、大きい問題をより小さな問題に分割して解く手法は、今後最適化問題を解く上で基礎となっていくと言えます。
さらに、今後量子ビットが増えることによって、より高速に厳密解を求めることができる可能性があります。
編集者あとがき
どうして量子コンピュータのみで解けないかというところで、クラスタリングが上手くいかない理由について少し疑問があるので、実際に試してみて確かにダメだなというのを確認できるとよいと思いました。また、現在D-Wave Advantage (約5,000量子ビット) が公開され、量子ビットは当時よりも増えているので、より良い解が発見できるようになっていると考えられます。
本記事の担当者
會田裕樹 (メンタリング:丸山尚貴、羽場廉一郎)