文献情報
タイトル: Graph Coloring with Quantum Annealing
著者:Julia Kwok, Kristen Pudenz
書誌情報:https://arxiv.org/abs/2012.04470
概要
グラフ彩色とは隣接した頂点対を異なる色になるように彩色することです。3色以上のグラフ彩色はNP困難であり、高速に計算することが困難な問題の一つです。したがって、厳密性を犠牲にした近似的な解を求めるのが妥当であると考えられています。近似解を求める方法の一つにグラフから独立点集合(どの頂点も隣接していない頂点の集合)を求め、一つの独立点集合ごとに1色ずつ割り当てる貪欲法があります。
本論文では、このアルゴリズムでグラフ彩色を行うときに独立点集合を量子アニーリングを用いて求めます。この提案手法を古典コンピュータで独立点集合を求めたときの結果を比較します。
問題
グラフ彩色の解法には、サブルーチンとして最大独立点集合を求める貪欲法が知られています。グラフ彩色問題と同様に最大独立集合問題もNP困難であり、高速に厳密な解を求めることは困難です。したがって、貪欲法や汎用最適化アルゴリズム近似的な解法による計算が一般的です。本論文では量子アニーリングで独立点集合を高精度に求めることで、グラフ彩色の貪欲法における最適化性能の向上を図ります。
方法
グラフ彩色の貪欲法
まずグラフ彩色を行う貪欲法の流れを導入します (図1参照)。今回はモンテカルロ法を用いて独立点集合を求めています。モンテカルロ法では確率的に解候補 (サンプル) を生成し、その中から最良解を出力します。全体のアルゴリズムは以下の手順1~4のようになります。
- グラフから独立点集合の候補を$ s $個求める
- 求めた候補の中から最も頂点数の多い独立点集合を選ぶ
- 選んだ独立点集合に1色割り当てて、その独立点集合をグラフから削除する
- グラフが空になったら終了、空ではなかったら1.に戻る
この貪欲法では全てステップで最大独立点集合を求めたとしても、最小色数の彩色が得られるわけではないため、彩色の最適性保証はないことに注意しましょう。
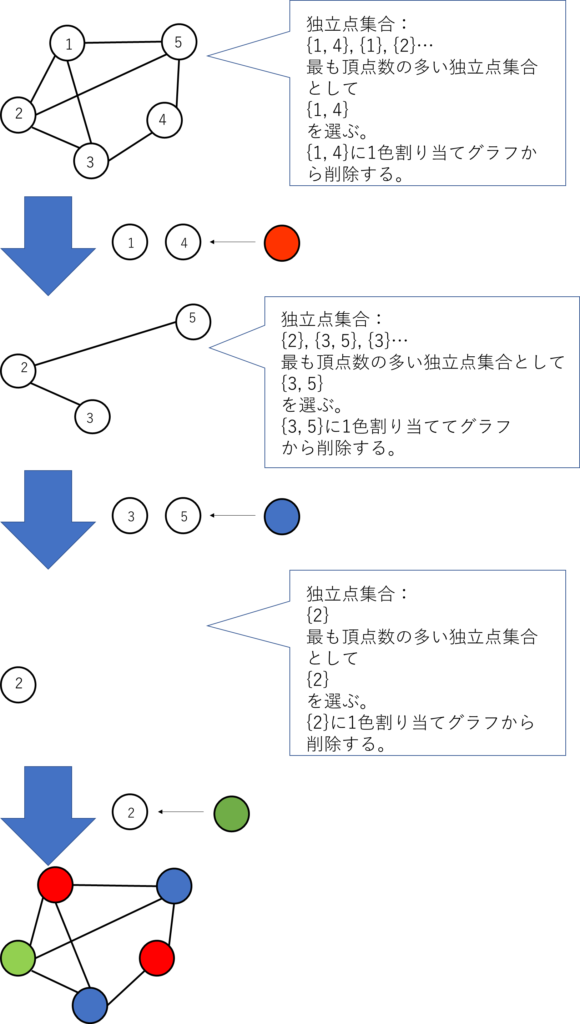
最大独立点集合の求め方
手順1で求める候補数$ s $を大きい値に設定すると、大きな独立点集合を見つけられる可能性は高くなる一方、実行時間が増加します。したがって、モンテカルロ法のアルゴリズムとしては、高速なサンプリングが可能で、かつ良質な解候補が得られることが望ましいと言えます。今回は量子アニーリングを用いて、独立点集合の解候補を生成します。
そのために、まず最大独立集合問題を定式化を行いましょう。グラフの頂点数を$ n $とします。各頂点に$ i=1,\cdots,n$と番号を割り振り$ x_{i}$を頂点$ i$を選ぶとき1、選ばないときに0になる2値変数を定義します。最小化するコスト関数は図2中の式で表せます。

このコスト関数の最小化はQUBO (Quadratic Unconstrained Binary Optimization) と呼ばれ、D-Waveマシンで実装可能な問題です。以上により量子アニーリングで独立点集合を求めることができます。
実験方法
量子アニーリングを用いた手法の有効性を検証するために、古典コンピュータを用いたグラフ彩色の近似アルゴリズム [1, 2]と比較します。このアルゴリズムでは、最大独立点集合のサイズを一定オーダーの近似率で抑えることで、高々$\chi \times \mathcal{O} \left(n (\log \log n)^2 (\log n)^{-3}\right) $ 個の色数で彩色が可能であることが証明されています。ただし、 $\chi $ は与えられたグラフの彩色に必要な最小の色数 (彩色数) です。
アルゴリズムを比較する際の基準となる3つの指標を導入します。
一つ目は成功確率です。$ r$回実行したときに$r_{s}$回成功したとすると成功確率$ p_{s}$は
\begin{equation}
p_{s}=\frac{r_{s}}{r}
\end{equation}
となります。
二つ目は実行時間です。$ r$回実行した内の$ i$回目の実行にかかった時間$ t_{i}$がであるとき実行時間の平均$ t_{wallclocktime}$は
\begin{equation}
t_{wallclocktime}=\frac{\sum_{i=1}^{r}t_{i}}{r}
\end{equation}
となります。ここでは古典コンピュータのみで彩色を行うときは一つのグラフを彩色を始めてから終えるまでの時間とします。また提案手法における$ t_{i}$は古典コンピュータの実行時間とD-Waveマシンの準備時間、量子アニーリングを行う時間の合計時間とします。このときインターネットのラグや埋め込みの時間は除外しています。$ s$を独立点集合の候補の個数、$ k$をグラフを彩色する色の数、$ r_{a}$を独立点集合を求められなかった回数とします。1色彩色するためには独立点集合を$ s$個求めます。求めた$ s$個の候補のすべてが独立点集合ではなかった場合はもう一度計算を行います。独立点集合の計算に失敗した回数を$ r_{a}$とします。すると、$ k$色彩色するのに求める独立点集合の候補の総数は$ s \times (k+r_{a})$個となります。以上より量子アニーリングの実行時間は
\begin{equation}
s \times (k+r_{a}) \times t_{sample}
\end{equation}
と表されます。$ t_{sample}$はアニーリング時間、読み出し、遅延の合計時間であり今回は370μsとなります。
D-Waveマシンの実行時間の詳細に関しては、こちらの資料をご参考ください [3]。
三つ目はTTS(Time To Solution)です。TTSは1回成功するために必要な時間を表しています。TTSは以下のように表されます。
\begin{equation}
TTS = \frac{\log(1-p_{target})}{\log(1-p_{s})} \times t_{wallclocktime}
\end{equation}
今回は$ p_{target}=0.99$としています。
結果
データとなるグラフは、頂点対に対してランダムに辺が与えて生成します。頂点数$ n$は$ n=20,40,60$として辺を生成する確率$ p$はそれぞれの$ n$について
\begin{equation}
p = \frac{c}{n} (c=4.5)
\end{equation}
とします。
量子アニーリングの解候補数$ s$に関しては、予め成功率と実行時間の観点から最適な$ s$を求めて、$ s=30$と設定します。古典コンピュータは$ s=1$とします。
結果を図3に示します。すべての指標で量子アニーリングが古典コンピュータを上回っており、今回の実験では量子アニーリングが古典コンピュータよりも良い性能を発揮しました。特に実行時間については量子アニーリングを行うときに読み出しや遅延の時間を考慮しても古典コンピュータよりも高速に実行できています。
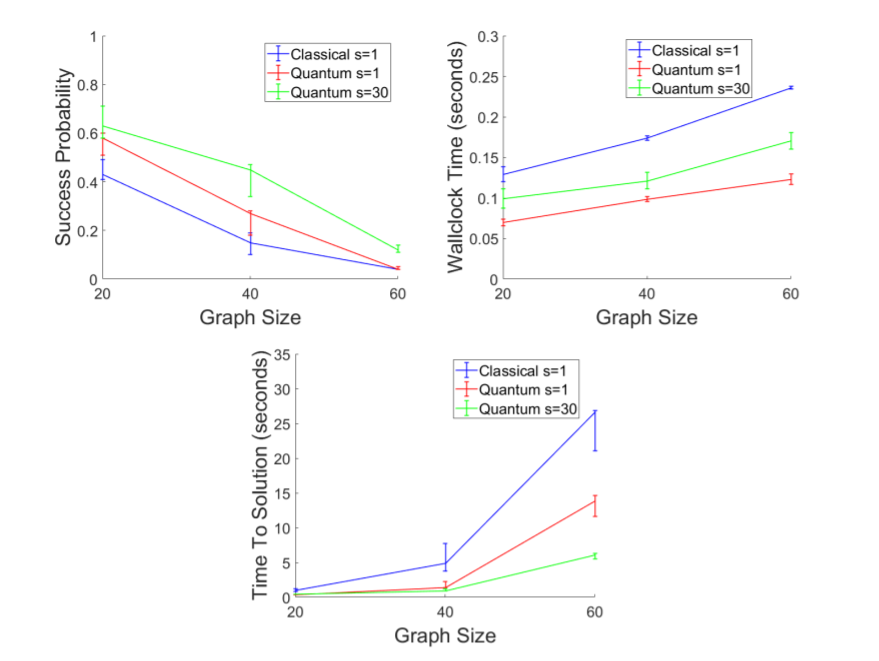
結論
今回の実験では量子アニーリングを用いて独立点集合を求めることで古典コンピュータで求めた時よりも高い性能を発揮しました。
しかし今回は頂点数が60までのグラフを用いており、より頂点数が多いようなグラフに対する彩色についても、量子アニーリングが優位であるかは不明です。また、今回はランダムグラフにおける検証であったが、実世界データに関しても量子アニーリングの優位性が保たれるかは興味深いです。
参考文献
[1] R.Bopanna and M.M.Halldórsson. Approximating maximum
independent sets by excluding subgraphs. BIT Numerical Mathematics,
32(2), pp. 180—196, 1992.
[2] M.M.Halldórsson. A still better performance guarantee for approximate graph coloring. Information Processing Letters, 45(1), pp. 19—23, 1993.
[3] D-Wave, D-Wave System Documentation, https://docs.dwavesys.com/docs/latest/c_qpu_timing.html
あとがき
今回の比較的小さいサイズの問題では量子アニーリングが優位になりましたが、結論でもあるようにより大きな問題などではどうなるか興味がわきました。今回使われた古典コンピュータで独立点集合を求めるアルゴリズムは別の記事で紹介しようと思います。