文献情報

タイトル : Music Composition Using Quantum Annealing

著者 : Ashish Arya, Ludmila BotelhoFabiola Canete, Dhruvi Kapadia, Ozlem Salehi

書誌情報 : 2201.10557.pdf (arxiv.org)

概要

コンピュータ科学の発展に伴い、｢ アルゴリズムによる作曲 ｣ という新しい分野が起こり、盛んに研究が行われるようになりました。そして、近年注目を集める量子コンピュータは、｢ アルゴリズムによる作曲 ｣ における新たなアプローチとなっています。しかし、これまでは量子ゲート方式を用いた研究が大半であり、量子アニーリング方式を用いた研究は未だほとんど行われていません。したがって、量子アニーリングがこの分野の発展に大きく寄与する可能性があります。

そこで、本論文では量子アニーリングを用いた新たな作曲手法を提案します。音楽を構成する要素をメロディ・リズム・ハーモニーの３つに分け、それぞれに対して D-Wave マシンを用いた生成方法を示します。

本記事では ｢ メロディ ｣ の生成に関する説明を行います。なお、本論文で紹介した作曲手法のプログラム ( Jupyterノートブック形式 ) が https://doi.org/10.5281/zenodo.585693 から参照可能です。

課題

本論文では、量子アニーリングを用いた作曲を行います。量子アニーリングは、組み合わせ最適化問題を解くことに特化したマシンであるため、作曲というプロセスを QUBO と呼ばれる形式の最適化問題に落とし込む必要があります。

作曲とは言っても、音をデタラメに並べるだけでは良い音楽はできません。音楽に関する様々な理論や規則に従って作曲を行うことにより、聴きなじみのある音楽が生成できます。また、既存の音楽に共通して見られるパターンを発見することも重要となります。これらの規則やパターンを、最適化問題における制約としてどのように定式化するかが課題となります。

方法

ここでは、作曲というプロセスを最適化問題として定式化する方法を紹介します。なお、本記事で必要となる音楽的な知識に関しては ｢ 5. 結論 ｣ の後に ｢ 6. 補足 : 音楽的な知識 ｣ として記載しています。

変数の定義

まずは、二値変数 $x_{i,j}\in\{0,1\}$ を定義します。D-Wave マシンで最適化問題を解いた結果として、この $x_{i,j}\in\{0,1\}$ の組み合わせが得られることになります。

ここでは、$n$ 個の音符を同時に生成し、それらを並べることによってメロディを生成することを目標とします。そこで、$i$ を何番目の音符かを示す文字とし、$i\in[n]$ と表します。ここで、$[n]$ は自然数の集合 $\{1,2, … , n\}$ です。また、$j$ をその音符の音の高さ ( ピッチ ) を示す文字とし、ピッチの集合を $P$ として $j\in P$ と表します。

上述のように、この集合の要素は ｢ ピッチ ｣ ですが、一口にピッチと言っても、様々な選び方が考えられます。また、それに伴って変数 $x_{i,j}$ における添え字 $j\in P$ の定義が変わることになります。本論文では、変数 $x_{i,j}$ の定義として以下に示す 3 つのものが紹介されています。

(1) $P$ を具体的な音名の集合とする

$P$ の要素として $ C4,D4,E4,F4$ といった具体的な音名を指定する方法です。このとき、変数 $x_{i,j}$ は以下のように定義されます。

$$ \begin{equation}x_{i,j} = \left \{\begin{array}{l}1　{\rm if}　(\ i\ 番目の音符は\ j\ ) \\0　{\rm otherwize} \end{array}\right.\end{equation} \tag{1} $$

ここで、$i\in[n]$ , $j\in P$ です。例えば、集合 $ P=\{C4,D4,E4,F4\}$ とすると、メロディとして生成される 4 個の音符は $ C4,D4,E4,F4$ のうちのどれかから選択されることになります。したがって、 $x_{2,C4}=1$ のとき、$n$ 個の音符のうち２番目の音符が $C4$ である、ということを表します。

(2) $P$ を半音による音階とする

半音によって音を識別する方法です。この方法では、基準となる最低ピッチと、現在考慮している音符の間にいくつ半音があるか、によって音を区別します。このとき、変数 $x_{i,j}$ は以下のように定義されます。

$$ \begin{equation}x_{i,j} = \left \{\begin{array}{l}1　{\rm if}　(\ i\ 番目の音符は最低ピッチから\ j\ 半音だけ離れている\ ) \\0　{\rm otherwize} \end{array}\right.\end{equation} \tag{2} $$

ここで、$i\in[n]$ , $j\in P$ です。$P=\{0,1,\ …\ ,12\}$とすると、集合 $P$ は半音を順番に 13 個並べた音階となるので、Chromatic Scale を表すことになります。

また、基準となる最低ピッチは自由に指定することができます。例えば、$j=0$ を $C4$ と対応づけると $P=\{0,1,\ …\ ,12\}$ は $C4$ から始まる C Chromatic Scale の音符の集合となります。したがって、$x_{2,2}=1$ のとき、$n$ 個の音符のうち 2 番目の音符は $C4$ から 2 半音だけ離れている ( つまり $D4$ ) ということを表します。

(3) $P$ の要素を全音階の 8 つの度数とする

$P=\{d_1,d_2,\ …\ ,d_8\}$ とおき、$d_j$ をその音階の $j$ 番目の度数とする方法です。このとき、変数 $x_{i,j}$ は以下のように定義されます。

$$ \begin{equation}x_{i,j} = \left \{\begin{array}{l}1　{\rm if}　(\ i\ 番目の音符の度数は\ d_j\ である\ ) \\0　{\rm otherwize} \end{array}\right.\end{equation} \tag{3} $$

ここで、$i\in[n]$ , $d_{j}\in P$ です。すなわち、$j$ は $P$ が表す音階の度数を指定します。したがって、$d_1,d_2,\ …\ ,d_8$ に設定する音階を変えれば、D-Wave マシンから得られた解を任意の音階に当てはめることが可能となります。

例えば、$P$ として C Major Scale を指定すると、$d_1=C,\ d_2=D,\ d_3=E,\ d_4=F,\ d_5=G,\ d_6=A,\ d_7=B,\ d_8=C$となります。したがって、$x_{2,1}=1$ のとき、$n$ 個の音符のうち 2 番目の音符は C Major Scale の 1 度 ( つまり $C$ ) ということを表します。

また、$P$として A Minor Scale を指定すると、$d_1=A,\ d_2=B,\ d_3=C,\ d_4=D,\ d_5=E,\ d_6=F,\ d_7=G,\ d_8=A$となります。したがって、$x_{2,1}=1$ のとき、$n$ 個の音符のうち 2 番目の音符は A Minor Scale の 1 度 ( つまり $A$ ) ということを表します。

以上が変数 $x_{i,j}$ の 3 つの定義でした。以降では (3) の定義を使用していきます。しかし、ピッチの集合 $P$ の定義を変えているに過ぎないため、以降で説明する制約は、(1) や (2) の定義を使用した場合にも共通するものになっています。

加えて、(1) の定義を用いれば、(2) や (3) で定義される集合 $P$ を表現することができます。例えば、(1) の定義のもとで、 $P=\{C,C\#,D,D\#,E,F,F\#,G,G\#,A,A\#,B,C\}$ とすれば、C Chromatic Scale となります。したがって、(2) の定義のもとで $P=\{0,1,\ …\ ,12\}$ とし、基準となる最低ピッチを $C$ に指定したときと同じ集合 $P$ が表現できます。

また、(1) の定義のもとで、 $P=\{C,D,E,F,G,A,B,C\}$ とすれば C Major Scale となり、 $P=\{A,B,C,D,E,F,G,A\}$ とすれば A Minor Scale となります。(3) の定義では、 $P=\{d_1,d_2,\ …\ ,d_8\}$ という抽象的な度数の列になっているため、生成された度数の列を C Major Scale に当てはめたり、A Minor Scale に当てはめたりすることが可能ですが、(1) の定義のもとで $P=\{C,D,E,F,G,A,B,C\}$ ( すなわち C Major Scale ) でメロディを生成したとしても、｢ $C$ → $A$ ｣、｢ $D$ → $B$ ｣、｢ $E$ → $C$ ｣ ･･･ というように音を読み変えれば、A Minor Scale に変換することができます。

なお、元の論文には (1) や (2) を定義として利用し、D-Wave マシンで実験を行った結果も記載されています。

制約の導入

目標は、D-Wave マシンを用いて、$n$ 個の音符を生成することです。ただし、生成される音符は、種々の音楽規則に則ったものである必要があります。したがって、まずはそれらの音楽規則を最適化問題における制約として定式化します。次に、それらの制約を含む最適化問題を D-Wave マシンで解くことができる QUBO 形式にするために、制約を除去する必要があります。具体的には、それぞれの制約を部分的な最小化問題に変換します。なお、制約を最小化問題に変換することを ｢ 緩和 ｣ と呼びます。

以下では、4 つの音楽規則を制約に落とし込み、それらを最小化問題に緩和する方法を紹介します。

制約① : $i$ 番目の音符のピッチは 1 つだけ

今、目標にしていることは、$n$ 個の音符それぞれに対してピッチを求めることです。したがって、$n$ 個の音符それぞれに 1 つずつピッチを指定しなければなりません。すなわち、ある 1 つの音符に対して、ピッチが指定されなかったり、あるいは複数のピッチが指定されたりすることを避ける必要があります。このような制約は、以下のように定式化することができます。

$$ \forall i \in [n],\ \ \sum_{j\in P} x_{i,j}=1 \tag{4} $$

式 (4) は、任意の $i \in [n]$ に対して $x_{i,j}=1 $ となるは 1 つだけ、ということを意味します。すなわち、$i$ 番目の音符に指定されるピッチ $j$ は 1 つだけ、ということです。この等式制約は、以下の最小化問題に緩和することができます。

$$ \min_{\vec{x}} \ \lambda_1 \sum_{i\in [n]} (1-\sum_{j\in P}{x_{i,j}})^2 \tag{5} $$

すなわち、式 (4) の等式が満たされなかった場合、その誤差が 2 乗されて足されるため、最小化に反することになります。したがって、式 (5) における $\sum_{i\in [n]} (1-\sum_{j\in P}{x_{i,j}})^2$ という項を、係数 $\lambda_1$ を掛けた上で目的関数に追加することにより、この制約を満たすような解が D-Wave マシンから得られるようになります。ここで言う目的関数とは、最小化問題における、最小化する対象の関数のことです。

なお、この制約は以降に続く制約の中で最も重要であるため、係数 $\lambda_1$ は十分に大きく設定します。係数が小さく設定された制約は、係数がより大きい制約に比べて優先度が低くなります。すなわち、目的関数全体の最小化のために、制約が破られる可能性が高くなります。

制約② : 同じ音を 3 回以上連続して出さない

同じ音がずっと続くと単調な楽曲になってしまうため、ここでは同じ音が連続するのを 2 回までに制限します。すなわち、同じ音を 3 回以上連続して出さないようにする制約を加えます。ここで、同じ音が 3 回出される、という状態は以下のように定式化することができます。

$$ \exists i \in [n-2],\ \ \exists j \in P,\ \ x_{i,j}=x_{i+1,j}=x_{i+2,j}=1 \tag{6} $$

すなわち、$i$ 番目の音符がピッチ $j$ で、$i+1$ 番目の音符もピッチ $j$ で、さらに $i+2$ 番目の音符もピッチ $j$ という状態です。これを防ぐためには、$x_{i,j} \ ,\ x_{i+1,j} \ ,\ x_{i+2,j}$ のうちどれか 1 つでも 0 になれば良いので、以下の最小化問題に緩和することができます。

$$ \min_{\vec{x}} \ \lambda_2 \sum_{j\in P}{\sum_{i\in [n-2]}{x_{i,j} \ x_{i+1,j} \ x_{i+2,j}}} \tag{7} $$

今、$x_{i,j} \in \{0,1\}$ であるので、$x_{i,j} \ ,\ x_{i+1,j} \ ,\ x_{i+2,j}$ のうちどれか 1 つでも 0 になれば、これらの積 $x_{i,j} \ x_{i+1,j} \ x_{i+2,j}$ は 0 になります。

制約③ : 最初と最後の音を指定

生成する楽曲において、最初と最後の音を指定できるようにします。ここでは、最初 ( $i=1$ 番目 ) の音と最後 ( $i=n$ 番目 ) の音を $P=\{d_1,d_2,\ …\ ,d_8\}$ の中の $d_1$ ( 1 度 ) に指定することにします。実際の作曲においても、楽曲の最初と最後の音を音階の 1 度 ( 主音 ) にすることが多いようです。したがって、 $i=1$ 番目の音符を $j=1$ ( 度 )、$i=n$ 番目の音符を $j=1$ ( 度 ) にする制約を加えます。この制約は以下のように定式化することができます。

$$ x_{1,1}=x_{n,1}=1 \tag{8} $$

すなわち、$x_{1,1}$ と $x_{n,1}$ が両方とも１になれば良いので、以下の最小化問題に緩和することができます。

$$ \min_{\vec{x}} \ \lambda_3 (-x_{1,1}-x_{n,1}) \tag{9} $$

今、 $x_{i,j} \in \{0,1\}$ であるので、 $x_{1,1}$ と $x_{n,1}$ が両方 1 になれば $-x_{1,1}-x_{n,1}$ は最小になります。

制約④ : 傾性音の取り扱い

音階の中には ｢ 傾性音 ｣ と呼ばれる、単体で鳴ると不安定な音があります。この傾性音が鳴った場合には、その次の音符を特定のものに指定する必要があります。具体的には、音階の ｢ 2、4、6 度の次には 1 度だけ下の音 ｣ を、 ｢ 7 度の次には 1 度だけ上の音 ｣ を指定します。この制約は以下のように定式化することができます。

$$ \begin{equation} \left \{\begin{array}{l} x_{i,2}=1\ ならば\ x_{i+1,1}=1 \\ x_{i,4}=1\ ならば\ x_{i+1,3}=1 \\ x_{i,6}=1\ ならば\ x_{i+1,5}=1 \\ x_{i,7}=1\ ならば\ x_{i+1,8}=1 \end{array}\right.\end{equation} \tag{10} $$

すなわち、$i$ 番目の音として、例えば音階の 2 度が選ばれてしまった ( $x_{i,2}=1$ ) 場合、次の $i+1$ 番目の音は音階の 1 度である ( $x_{i+1,1}=1$ ) 必要がある、ということになります。一方、$x_{i,2}=0$ であれば、そもそも傾性音が鳴らないため、問題にはなりません。 $i$ 番目の音が 4 度、6 度、7 度であった場合についても同様のことが言えます。以上を踏まえて、傾性音に関する制約は以下の最小化問題に緩和することができます。

$$ \min_{\vec{x}} \ \lambda_4 \sum_{i \in [n-1]}{\{ x_{i,2}(1-x_{i+1,1}) + x_{i,4}(1-x_{i+1,3}) + x_{i,6}(1-x_{i+1,5}) + x_{i,7}(1-x_{i+1,8}) \} }\tag{11} $$

例えば、$x_{i,2}(1-x_{i+1,1})$ という項について考えると、$x_{i,2}=1$ かつ $x_{i+1,1}=0$ のとき $x_{i,2}(1-x_{i+1,1}) =1$ となり、式 (11) の全体が大きくなってしまいます。したがって、$x_{i,2}=1$ ならば $x_{i+1,1}=1$ となることを求める定式化になっています。すなわち、この項は ｢ 2 度の次は 1 度 ｣ という制約に対応しています。他の 3 つの項 $x_{i,4}(1-x_{i+1,3}) $、$x_{i,6}(1-x_{i+1,5}) $、$x_{i,7}(1-x_{i+1,8})$ についても同様に考えることができ、それぞれ ｢ 4 度の次は 3 度 ｣、｢ 6 度の次は 5 度 ｣、｢ 7 度の次は 8 度 ｣ という制約に対応しています。

報酬の導入

これまでは、目的関数に制約のみを加えてきました。したがって、制約に違反しない音符の列は全て実行可能解 ( 目的関数を最小にする解 ) ということになります。よって、今度はそれらの実行可能解を区別するために、目的関数に ｢ 報酬 ｣ を導入します。ここでは、以下に示すように、特定の音が連続したときに、目的関数を減少させる項を追加します。

$$ -\lambda’ \sum_{ \substack {i \in [n-1] \\ j,j’ \in P} }{W_{j,j’} \ x_{i,j} \ x_{i+1,j’}} \tag{12} $$

ここで、$W_{j,j’}$ は $i$ 番目の音が $j$ 、$i+1$ 番目の音が $j’$ であったときの報酬の大きさ ( 重み ) を表す係数です。ピッチの組み合わせごとに重みを設定するため、$W_{j,j’}$ は行列です。この重みの行列は既存の楽曲を分析し、連続する音符を調べることによって形成します。

ここでは、例としてベートーヴェン ( Beethoven ) の ｢ 歓喜の歌 ( Ode to Joy ) ｣ の一部を取り上げます。その抜粋部分を以下の図 1 に示します。

図 1 の楽譜にある 15 個の音符から、連続する音符のペア ( 14 ペア ) を数え上げ、その出現回数を重みとします。すると、以下のように行列 $W_{j,j’}$ の成分が設定されます。

$$ \begin{equation} \begin{split} W_{F\#4,E4}=2,\ W_{F\#4,F\#4}=2,\ W_{F\#4,G4}=1,\ W_{G4,F\#4}=1, \ W_{G4,A4}=1, \\ W_{A4,G4}=1,\ W_{A4,A4}=1,\ W_{E4,D4}=1, \ W_{E4,E4}=1, \\ W_{E4,F\#4}=1,\ W_{D4,D4}=1,\ W_{D4,E4}=1 \end{split} \end{equation} \tag{13} $$

なお、ここで設定した $W_{j,j’}$ は $j,j’ \in P \times P$ の全要素を含んでいるわけではありません。したがって、それらのペアの重みは全て０ということになります。しかし、重みが０だとしても、報酬が設定されていないだけであって、対応する音のペアが制約として避けられるわけではありません。

また、ある音のペアが ｢ 制約 ｣ と ｢ 報酬 ｣ の両方を持っていた場合には、｢ 制約 ｣ の方が優先される必要があります。すなわち、目的関数が ( 違反による増加 ) > ( 報酬による減少 ) となるように係数 $\lambda’$ を調整します。

結果

これまでに導入してきた制約や報酬を目的関数に追加し、D-Wave マシンを用いて実際に解を求めた結果を示していきます。すなわち、D-Wave マシンを用いて、目的関数に関する最小化問題を近似的に解きます。D-Wave マシンから得られる解は、必ずしも目的関数を最小にする解とは限らないため、D-Wave マシンから得られる複数の解の候補の中から、目的関数が一番小さくなっているものを選択します。ここで、目的関数とは、これまでに導入してきた報酬項や制約項を足したものです。

はじめに、制約 ①、③、④ を適用して D-Wave マシンによって解を求めた結果を示します。制約 ①、③、④ に対して定義した最小化問題 ( 式 (5)、(9)、(11) ) を目的関数に追加し、QUBO 形式にした上で、D-Wave マシンから変数 $x_{i,j} \in \{ 0,1\}$ の組み合わせを取得しています。D-Wave マシンから得られた解を C Major ( 上 )、G Minor ( 下 ) で楽譜にしたものを以下の図 2 に示します。

図 2 の五線譜の上にある数字が度数に対応します。例えば ｢ 1 ｣ は $P=\{d_1,d_2,\ …\ ,d_8\}$ の ( 1 度 ) にあたります。上の楽譜と下の楽譜とでは使用している音階が異なるため、音符の列の見た目は異なりますが、D-Wave マシンから得られた解は同じものを使用しているので、度数の列は一致しています。

度数の列を見ると、最初と最後の音符の度数が１度になっていることが分かります。したがって、制約 ③ が守られています。また、4 度の次は 3 度、6 度の次は 5 度、7 度の次は 8 度上となっています。従って、制約 ④ が守られていることも確認できます。しかし、今回は連続した音に関する制約 ② を適用していないため、度数 3 の音が 3 回続いている箇所が見られます。

次に、制約 ①～④ ( 式 (5)、(7)、(9)、(11) ) に加え、報酬項 (式 (12) ) を目的関数に追加した上で、D-Wave マシンを用いて解を求めた結果を示します。D-Wave マシンから得られた、目的関数を最小にする解を「歓喜の歌」と同様の音階 ( D-Minor ) で楽譜にしたものを以下の図 3 に示します。

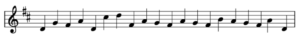
図 3 の楽譜が示すように、制約 ③ を加えたことにより、今回は 3 回同じ音が続くことがなくなりました。また、最初と最後を 1 度の音 ( ここでは $D4$ ) にする制約 ④ も守られています。

そして、譜面には ｢$\ G4,\ F \# 4 \ $｣ というパターンが 4 回、｢$\ A4 , \ G4 \ $｣ というパターンが 3 回現れています。これは、$\ W_{G4, F \# 4}=1 \ $ や $\ W_{A4 , G4}=1 \ $ という重みを加えた効果だと考えられます。しかし、｢$\ F\#4 ,\ E4 \ $｣ や ｢$\ F\# 4 ,\ F\#4 \ $｣ のように、より大きな重み ($ \ W_{F\#4 , E4}=2,\ W_{F\# 4 , F\#4}=2 \ $) を設定したペアは出現しませんでした。これは、報酬に比べて制約の優先度が大きかったためであると予想されます。したがって、制約や報酬の優先度を決定する係数 $\lambda_1,\ \lambda_2,\ \lambda_3,\ \lambda_4,\ \lambda’ $ を適切に設定することが重要だと考えられます。

結論

量子アニーリングを用いてメロディを生成するために、作曲というプロセスを最適化問題として定式化する方法を検討してきました。具体的には、様々な音楽規則を制約として定式化する方法を提案しました。また、既存の楽曲における、連続する音符のペアに報酬を与えることにより、その楽曲に近い曲を生成する方法を導入しました。

実験結果から、D-Wave マシンを用いて、制約に従った楽曲が生成できることが分かりました。また、各種制約および報酬の優先度を決める係数を適切に調整することが重要であることが分かりました。

補足 : 音楽的な知識

ここでは、本記事において必要になる音楽的な知識を簡単に説明します。

はじめに、音の名前 ( 音名 ) を表現するために日本で使われている ｢ ド･レ･ミ･ファ･ソ･ラ･シ ｣ という表記は、英語では ｢$\ C \cdot D \cdot E \cdot F \cdot G \cdot A \cdot B \ $｣ という表記に対応します。本記事では、後者の英語での表記を用います。したがって、例えば ｢$\ C \ $」と書いたときには ｢ ド ｣ の音を指し、｢$\ D \ $｣ と書いたときには ｢ レ ｣ の音を指します。

また、ピアノの鍵盤上での ｢$\ C \cdot D \cdot E \cdot F \cdot G \cdot A \cdot B \ $｣ の配置は以下の図 4 のようになります。図 4 の鍵盤には ｢$\ C \ $｣ が 2 回登場していますが、このように鍵盤上には同じアルファベットの音がいくつも存在します。したがって、｢$\ C4 \ $｣ や ｢$\ C5 \ $ ｣ のようにアルファベットと数字で書くことにより、どの ｢$\ C \ $｣ なのかを区別します。他のアルファベットについても同様です。なお、同じアルファベット同士の ｢ 音の高さの差 ( = 音程 ) ｣ を 1 オクターブと呼びます。したがって、例えば ｢$\ C4 \ $｣ と ｢$\ C5 \ $｣ は 1 オクターブ離れており、｢$\ B4 \ $｣ と ｢$\ B6 \ $｣ は 2 オクターブ離れています。

五線譜上における ｢$\ C \cdot D \cdot E \cdot F \cdot G \cdot A \cdot B \cdot C\ $｣ の配置を以下の図 5 に示します。五線譜の上の方に行くほど、音は高くなります。

次に、音階について説明します。音階とは、複数の音をその高さに応じて順番に並べたものです。音階には様々な種類がありますが、主要なものとして長音階 ( メジャースケール : Major Scale ) と短音階 ( マイナースケール : Minor Scale ) が知られています。Major Scale と Minor Scale は 5 つの ｢ 全音 ｣ と 2 つの ｢ 半音 ｣ からなる全 7 音の音階で、Major Scale と Minor Scale を総称して全音階 ( ダイアトニックスケール : Diatonic Scale ) と呼びます。

ここで、半音とは、図 4 の鍵盤上の ｢$\ E \ $と$\ F \ $｣ や ｢$\ B \ $と$\ C \ $｣ といった、黒鍵を挟まない音同士の音程を指します。また、｢$\ C \ $と$\ C\# \ $｣ や ｢$\ C\# \ $と$\ D \ $｣ といった、隣り合った白鍵 ･ 黒鍵同士の音程も半音です。この半音は音程の最小単位となっています。また、全音とは、半音の 2 倍の音程のことを指します。従って、｢$\ C \ $と$\ D \ $｣ や ｢$\ E \ $と$\ F\# \ $｣ といった、半音 2 つ分の音程が全音です。

Major Scale と Minor Scale は、それぞれ ｢ 明るい印象 ｣ の音階と ｢ 暗い印象 ｣ の音階として知られています。図 4 の鍵盤において、黒鍵を含めずに、白鍵を$\ C \ $から並べた音階 ｢$\ C\cdot D\cdot E\cdot F\cdot G\cdot A\cdot B\cdot C\ $ ｣ は、$\ C \ $から始まる ($\ C \ $を主音とする ) Major Scale ということで C Major Scale と呼ばれます ( ここでは 1 オクターブ上の$\ C \ $を含めています )。このときの音程の列は、図 4 の鍵盤の下にあるように ｢ 全音･全音･半音･全音･全音･全音･半音 ｣ となっています。

一方、同様に白鍵のみを並べた音階でも、$\ A \ $から始まる音階 ｢$\ A \cdot B \cdot C \cdot D \cdot E \cdot F \cdot G \cdot A\ $｣ は、$\ A \ $を主音とする Minor Scale ということで A Minor Scale と呼ばれます。このときの音程の列は、以下の図 6 に示すように ｢ 全音･半音･全音･全音･半音･全音･全音 ｣ となっており、Major Scale と比較すると全音と半音の組み合わせが異なります。これが Major Scale と Minor Scale の印象の違いに繋がります。[1]

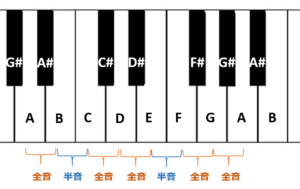
また、半音階 ( クロマチックスケール : Chromatic Scale ) と呼ばれる音階があります。これは、半音を 12 個 ( 1 オクターブ上の音を含めたら 13 個 ) 並べた音階です。図 4 の鍵盤上で$\ C \ $から白鍵と黒鍵を並べた音階 ｢$ \ C \cdot C\# \cdot D \cdot D\# \cdot E \cdot F \cdot F\# \cdot G \cdot G\# \cdot A \cdot A\# \cdot B \cdot C \ $｣ は C Chromatic Scale と呼ばれます。

これまで、｢$ \ C \cdot D \cdot E \cdot F \cdot G \cdot A \cdot B \cdot C \ $｣ ( C Major Scale ) や ｢$ \ A \cdot B \cdot C \cdot D \cdot E \cdot F \cdot G \cdot A \ $｣ ( A Minor Scale ) のように、音階を構成する音名を並べて表記してきましたが、このような 8 つの音は ｢$\ 1 度 \cdot 2 度 \cdot 3度 \cdot 4度 \cdot 5度 \cdot 6度 \cdot 7度 \cdot 8度 \ $｣ のように ｢ 度数 ｣ と呼ばれる単位で表されることがあります。例えば、C Major Scale の ｢$\ C \ $｣ は 1 度、｢$\ D \ $｣ は 2 度、･･･、1 オクターブ上の ｢$\ C \ $｣ は 8 度になり、A Minor Scale の ｢$\ A \ $ ｣ は 1 度、｢$\ B \ $｣ は 2 度、･･･、1 オクターブ上の ｢$\ A \ $｣ は 8 度になります。

あと書き

量子アニーリングを作曲に使おうというアイデアが面白いと感じました。加えて、量子アニーリングが応用できる領域を広げる意味でも価値のある研究だと思いました。また、｢ アルゴリズムによる作曲 ｣ という研究分野があることを初めて知りました。現在の主流は機械学習を使った方法だそうなので、これに関しても調べてみたいと思いました。

今回、D-Wave マシンを使って実際にメロディを生成していますが、どのようなメロディを好むかは人によって異なるため、生成された楽曲が果たして ｢ 良い ｣ 音楽なのか、という評価を定量的に行うことは難しいと感じました。したがって、芸術作品としての評価というよりも、設定した音楽規則がどの程度守られているか、もしくは既存の楽曲にどの程度近いか、といった評価になるのが特徴的だと感じました。

また、本論文では、既存の楽曲における連続する音のペアに重みをつけて報酬としていました。しかし、それだけでは、生成される楽曲が既存の楽曲に頻出する音のペアを含みやすくなるだけで、元の曲の特徴を掴んだことにはならないのではないかと感じました。したがって、報酬を与える対象や、その定式化の方法に関しては改善の余地があると思いました。

参考

[1] 音階の仕組み ❶全音と半音 – SoundQuest ：https://soundquest.jp/quest/prerequisite/scale-2/

本記事の担当者

高林泰成 (メンタリング：丸山尚貴、羽場廉一郎)