文献情報

タイトル：Multi-car paint shop optimization with quantum annealing
著者：Sheir Yarkoni, Alex Alekseyenko, Michael Streif, David Von Dollen, Florian Neukart, Thomas Bäck
書誌情報：arXiv:2109.07876

概要

マルチカーペイントショップ問題は、「車に塗る塗料の色の変更回数をいかに少なくするか」という最適化問題である。そしてこの問題は、NP困難であることがわかっている。この論文では、マルチカーペイントショップ問題をイジングモデルとして定式化する方法を示す。そして、従来の古典アルゴリズム(貪欲法)、D-Waveの量子アニーリングマシンとハイブリッドソルバを比較した。ハイブリッドソルバとは量子アニーリングと古典的な手法を組み合せたアプローチであり、D-Waveによって提供されている。検証の結果、小規模な問題 (10~100台程度の塗装問題) では量子アニーリングマシンが、大規模な問題 (300~3000台程度の塗装問題) ではハイブリッドソルバが適していることがわかった。一方、大規模な問題に対しては、貪欲法との大きな性能差は見られなかった。

背景・課題

量子コンピュータの登場で古典コンピュータよりも高速な計算が可能になることが期待され、それに関する実証実験が盛んになされている。しかし、産業上の最適化問題の多くは様々な変数の種類（例えば、整数値や連続値）が混ざり合った複雑なモデルである一方、現在公開されている量子コンピュータでは小さいスケールの二値最適化問題にしか対応できない。そのため、量子コンピュータを利用した大規模なアプリケーションは未だ現れていないのが実情である。そこで筆者らは実機で適用可能な産業問題を見つけることを主眼に置いた。本論文では自動車産業の課題として、Volkswagenの自動車製造に欠かせない工程である車両の塗装順の計算をマルチカーペイントショップ問題として定義し、そのソルバとして量子アニーリングマシンの有効性を評価する。

方法

マルチカーペイントショップ問題

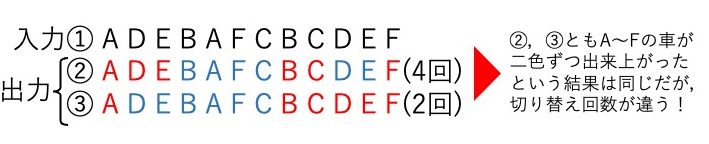
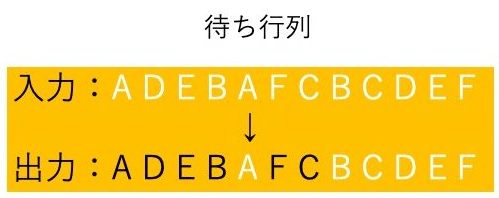
マルチカーペイントショップ問題とは、入力として塗装される車両の列および各車種に対して各色の目標塗装台数が与えられたとき、色の切り替えが最小となるような各車両に対する色の割り当てを求める問題である。ここで、色の切り替えとは、ある車両を塗る際にその前の車両の塗装色とは異なる色となることを指す。ベルトコンベアー上に並ぶ車考えたとき、これを前から順番に色を塗る際に、色の切り替えを最小にして着色できれば、最適化が行われたということになる。最適化は次のような方法で行われる。同じ種類の車が後ろにあるならば、前の車は前後と同じ色を塗り、後ろにその前の車が塗られるはずだった色を塗れば、切り替え回数を減らすことに繋がる。図1の例ではアルファベットを車両の種類に見立てて車の待ち行列を表現している。入力は行①のようになっていて、塗る色はそれぞれのアルゴリズムを用いて決められる。行②と行③は違ったアルゴリズムで解かれた出力である。ここで、行②の2番目のDという種類の赤い車両と10番目のDという青い車両は、車両としては同じ種類でも塗装する色が違うだけなので、前後で塗る色を入れ替えても出力される車の内容は変わらない。よって、交換しても出力される結果は変わらない。これをEという車両でも繰り返すことにより、この例では色の切り替え回数を行②の4回から③の2回に改善することができた。

イジングモデルとして定義する

ここでは、イジングモデルによりマルチカーペイントショップ問題を表現する方法を示す。今回は二色の塗装について扱う。まず、スピンの向きと塗装される色を結びつける。$ i $番目のスピンの変数をとおくと、上向きのスピン($s_i=+1$のとき)は黒を、下向きのスピン($s_i=-1$のとき)は白を塗装することとする。まず、隣り合う車は同じ色であってほしい、つまり同じスピンの向きをしていてほしいので、そうなっている割合が高いほど値が小さくなるようなハミルトニアンを考える。すると、式(1)のように書ける。

\begin{equation}
H_A =\,- \sum^{N-2}_{i=0} s_i s_{i+1}\tag{1}
 \end{equation}

これを見ると、シグマ記号の中身の項では、隣り合うスピンが同じ値であれば1が、異なる値であれば-1が加算されていき、その総和にマイナスがつけられているので、総和の値が大きいほど結果は小さくなることが分かる。これによって目的関数(目標を満たすほど値が最小化される関数)が表現できた。

次に制約条件を設ける。これは、顧客の注文に応じて決まった数の車が白や黒に着色されることを保証するものである。まず、車の待ち行列を$\omega$とし、$\omega$の$j$番目の車を$\omega_j$とする。各車両に対して$ \{ C_0, C_1, \cdots, C_{M-1} \} $ から一種類の車種が予め定められている。ただし、$M$は車種の総数である。すると、$C_l ~ (l \in \{1, 2, \cdots, M-1\}) $という車種が、$\omega$の何番目にいるかを示す $A(C_l)$という集合を式(2)のように書ける。

\begin{equation}
A(C_l) := \{j | \omega _ j = C_l, j = 0, … , N-1\}
\end{equation}

ここで簡単のために、一旦0または1の値を取る二値変数$x_j$を用いて制約条件を定義しよう。

\begin{equation}
 x_j:=
 \begin{cases}
  1 &\text{$\omega_jを黒で塗る$}\\
  0 &\text{$\omega_jを白で塗る$}\\
 \end{cases}
\end{equation}

とおくと、待ち行列のうち車種$C_l$が黒に塗られる台数を$\#C_l|_B:=\sum_{j\in A(C_i)} x_j$と書ける。ここで、車種$C_l$に対して黒に塗る車の台数が$k(C_l)$として定まっているとすると、全ての$l \in \{1, 2, \cdots, M-1\}$について、$\#C_{l|B} =k(C_l)$という関係が満たさなければならない。

この等式制約は、それぞれの$l \in \{1, 2, \cdots, M-1\}$について罰金法というテクニックを用いることで、次のようにハミルトニアンを定義することができる。

\begin{eqnarray}
H_B &=& \left( k(C_l)-\sum_{j\in a(C_l)} x_j \right)^2\\
&=& (k(C_l))^2-2k(C_l)\sum_{j\in A(C_l)} x_j +\left( \sum_{j\in A(C_l)} x_j \right)^2\\
&=& 2\sum_{i<j \in A(C_l)}x_i x_j + \lbrace 1-2k(C_l)\rbrace \sum_{j\in A(C_l)} x_j + (定数)
\end{eqnarray}

ここで$x_j= (s_j + 1) / 2$を代入し、0または1の値を取る変数から-1または1の値を取るイジングモデルの変数に対応させる。

\begin{eqnarray}
H_B &=& 2\sum_{i<j \in A(C_l)}\frac {s_i+1}{2}\frac {s_j+1}{2} + \lbrace 1-2k(C_l)\rbrace\sum_{j\in A(C_l)} \frac {s_j+1}{2} \\
&=& \frac{1}{2}\sum_{i<j \in A(C_l)}s_i s_j+\frac{1}{2}(\#C_l-1)\sum_{j\in A(C_l)}s_j+\frac{1}{2}(1-2k(C_l))\sum_{j\in A(C_l)}s_j+(定数)
\end{eqnarray}

ただし、$\#C_l = \sum_{j}1$であり、$\#C_l$は車種$C_l$の台数に等しい。式全体の定数倍や定数項は最小化問題に影響しないので、きれいに書き直すと次のようになる。

\begin{equation}
H_B :=(\#C_l-2k(C_l))\sum_{j\in A(C_l)}s_j + \sum_{i<j \in A(C_l)}s_i s_j
\end{equation}

以上のハミルトニアンを足し上げることで、マルチカーペイントショップ問題が次式のハミルトニアンで表されるイジングモデルとして定義できる。

\begin{equation}
H_{MPCS}=\,- \sum^{N-2}_{i=0} s_i s_{i+1}+\lambda\sum_{C_l\in C}\Biggl \lbrack (\#C_l-2k(C_l))\sum_{j\in A(C_l)}s_j + \sum_{i<j \in A(C_l)}s_i s_j \Biggr \rbrack \tag{3}
\end{equation}

$\lambda$ は目的関数に対する制約項の強さに対応し、最適解が制約を満たすように十分に大きな値に設定する必要がある。今回は制約は重要な条件であることから、その制約が守られていることを保証するために、$\lambda$には$\lambda = N$を代入してイジングモデルを作った(巻末資料にて解説)。

実験方法

データの用意

まず最適化をする対象のデータソースの確保を行った。フォルクスワーゲンの塗装工場より実際に顧客から注文された車のデータを収集し、合計104,334台の車について検証を行った。季節的な偏りがないように六週間に一回の集計で一年間、全部で121種類の車のデータを集めた。そのうち13種類は一度しかリクエストされていないことから、最適化の対象から除外した。

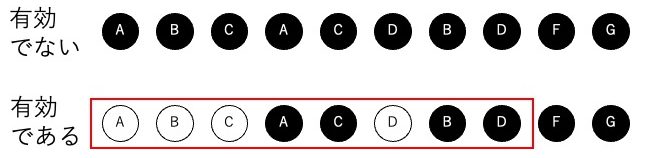
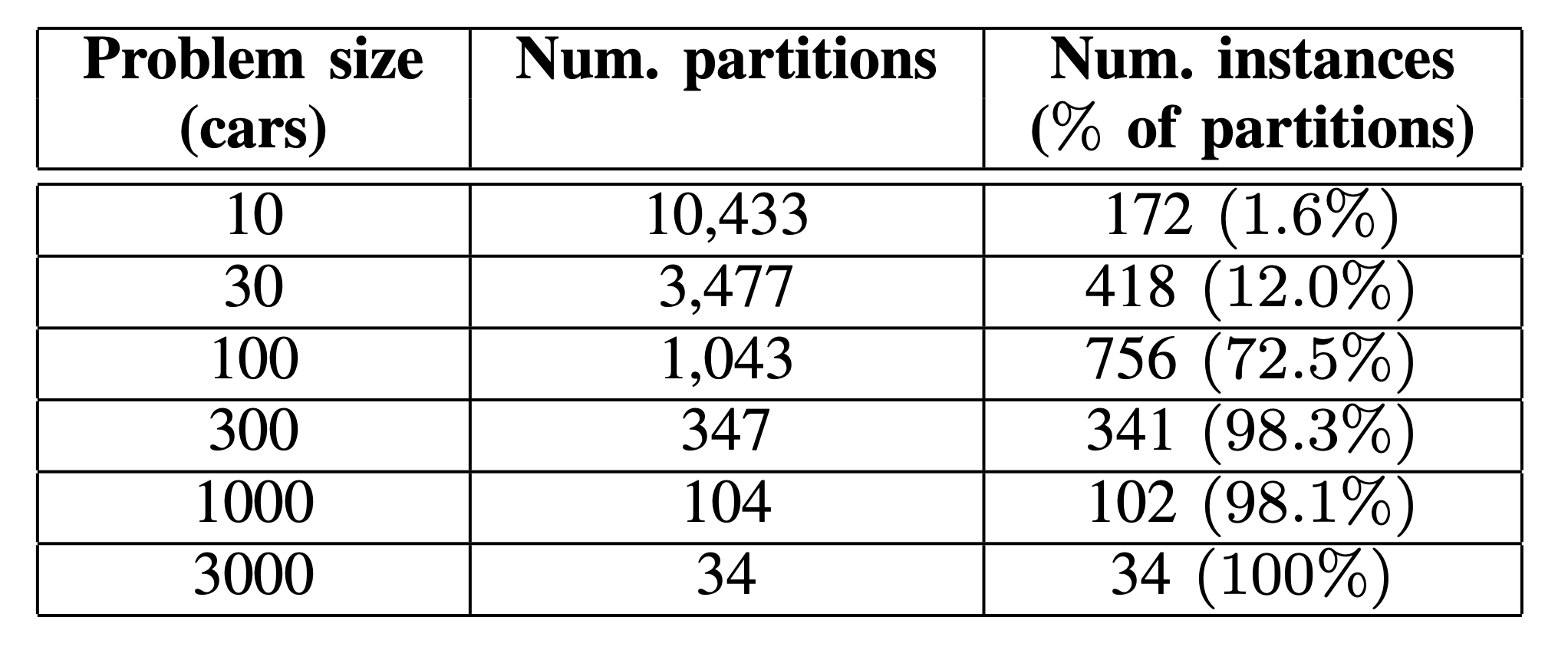
そして、実際に集計した104,334台について、問題サイズ (待ち行列の台数) を設定してデータを分割する。問題サイズを変化させて10～3000台のデータに分けた。分割された問題数をパーティション数とし、それは床関数を用いて$\lfloor\frac{104,344}{N_{cars}}\rfloor$となる。(ただし$N_{cars}$は問題サイズ)。そこから有効なインスタンスを50個選び、最適化の対象とする。有効なインスタンスとは、「70%以上の車が白黒どちらの色に塗られてもいい車である場合、それを有効なインスタンスとする」と定義されたものである。なぜこのような定義が必要かというと、すべての車が黒または白に塗られる場合の待ち行列は最適化の必要がないためである。図2にその例を示す。よって、入れ替えの必要ないインスタンスは選ばず、車の入れ替えが可能な待ち行列を採用した。

　そして、それぞれの問題サイズとそれに対するパーティション数、有効なインスタンスの割合を以下の表１に示す。

最適化の方法　

ここでは、イジングモデルの解を求める手段を６つ示す。

まず一つ目はランダムである。これは最適化なしで、先着順に車のデータに応じて着色していく方法である。

二つ目ブラックファーストである。マルチカーペイントショップ問題を解くため貪欲に探索するアルゴリズムである。方法としては、先頭から次に白を塗らなければならない状況になるまで黒を割り当てていくアルゴリズムである。図3に例を示す。貪欲に得られた解は、問題サイズに比例して色変更の回数も増え、少数の場合を除いて最適でない。

三つ目はシミュレーテッドアニーリングである。金属の温度を上げ、冷ましていく過程で秩序のある構造を作り出す様子を古典コンピュータで再現したものである。このアルゴリズムを使って最適化を行う。

四つ目は量子アニーリングである。これは、量子揺らぎによってイジング模型の基底状態(最低エネルギー状態)を求めることで組み合わせ問題を解くヒューリスティックアルゴリズムである。ここでは量子アニーリングマシンとして、D-Wave 2000QとAdvantageを利用する。

五つ目はタブーサーチである。タブーサーチでは現在の解$x$の近傍にある解$x’$に移動する操作を限りなく繰り返し、最適解を探っていく方法である。しかし、無限に解を探索しないようにタブーリストを作っておいて、すでに探索した解には行きつかないようにすることで局所解を探索し、最適化を行う。

六つ目はD-Waveの提供するハイブリッドソルバである。300台以上の問題では、量子アニーリングマシンで解くことができなくなったので、ハイブリッドソルバという量子アニーリングと古典的な解法を組み合わせた方法で解く手法を採用する。このアルゴリズムでは、任意の構造を持つイジングモデルやQUBOを最大1万変数まで解けるように設計されている。

結果

それぞれの最適化の手法の評価は、ランダムにより得られた解における塗装の色の交換回数との差をもとに比較を行った。その結果を図4に示す。問題サイズが100以下であれば、ブラックファースト(Greedy)のアルゴリズムに対して、シミュレーテッドアニーリング、ハイブリッドソルバ(HSS)は上回り続けたが、問題サイズが300以上になってくると、シミュレーテッドアニーリングは時間がかかりすぎて途中で解を導けなくなり、ハイブリッドソルバは最終的にブラックファーストとほぼ同様の結果となった。

また、すべてのソルバの出力結果を表2に示す。

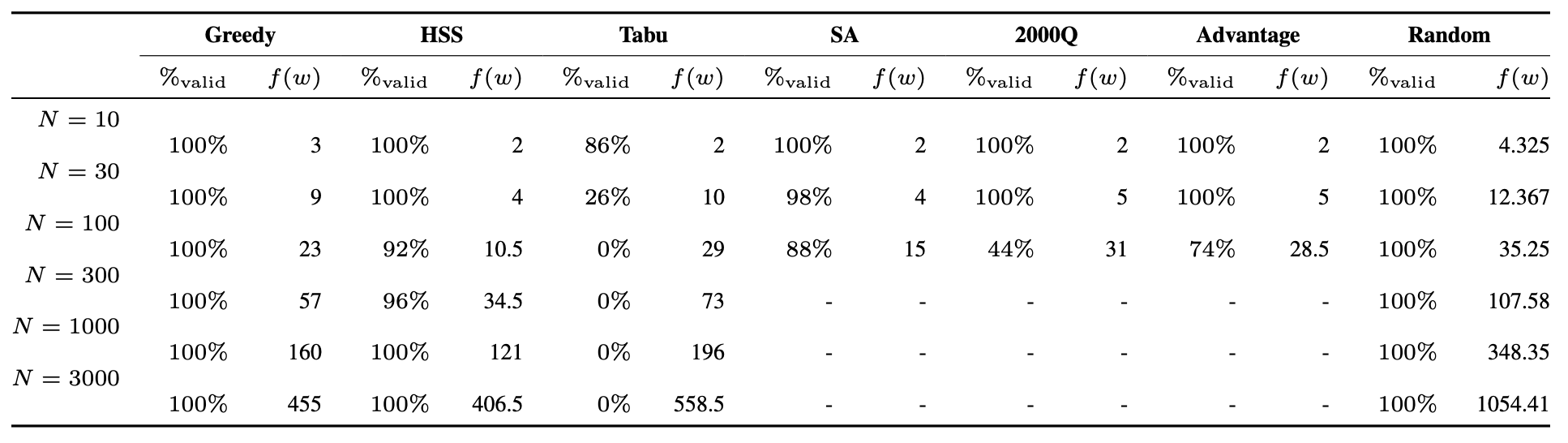
この中で、ハイブリッドソルバは100～300台で制約を満さない解をいくつか生成していた。その要因として、二つ挙げられる。

一つ目は、問題サイズの増加により、イジングモデルをグラフを用いて表現した問題グラフ上において、相互作用が密となってしまうためである。まず、問題グラフについて説明する。待ち行列の車種$C_l$を黒で塗らなければならない台数は$k(C_l)$で与えられていた。この車種$C_l$ごとにどの車を黒に塗らなければいけないかを、$k(C_l)-hot$制約という黒に塗られる車両は1のビットを立たせ、他は0とした際に、1のビットは$k(C_l)$個でなければならない制約を守って決めなければならない。この制約を守った車種$C_l$毎に完全グラフ構造が生じる。これにより問題サイズの増加に比例して待ち行列内の各車種の台数が増加することで。完全グラフの頂点数が増加する。問題の複雑さが増した（問題グラフが密となった）ことから、問題を解くことが難しくなったと考えられる。

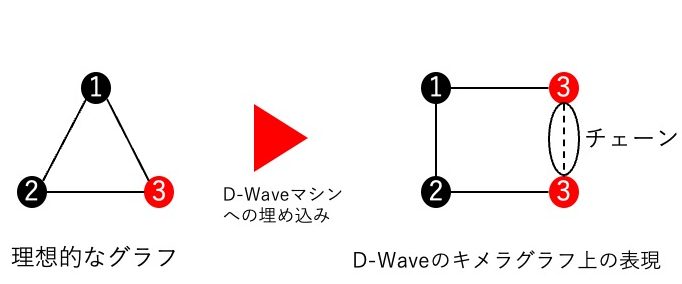
さらに、D-Waveマシンに問題を解かせる場合に、それをD-Waveマシンの構造であるキメラグラフ(図5参照)に埋め込む際に冗長な量子ビットが必要となる。この冗長なビットを紐づける構造をチェーン(図6参照)と呼び、チェーンは問題サイズが大きいほど長くなり、強い強度が必要になる。その影響により、問題サイズが大きくなることで問題を解くことが難しくなったのではないかと筆者は考えている。

二つ目は、問題サイズの増加によって符号化精度が落ちることである。式(3)で$\lambda=N$と定義していた。それにより、ハミルトニアン$H_B$は$H_A$に比べて、マルチカーペイントショップ問題の定式化に必要な数値精度は$1/N$に比例して下がってしまう。これによって近似解と最適解の区別がつきにくくなった。また、問題サイズ$N$に比例してD-Waveマシンにおけるチェーン(図6の状態)の強さが増すので、符号化精度は$1/N^2$となる。これによって、大規模な問題では、解の精度が非常に低くなる可能性がある。以上の二つの理由により制約を満たさない解を導き出したと考えられる。

結論

今回、マルチカーペイントショップ問題を実際の塗装工場のデータを用いて、古典的な手法と量子アニーリングマシンを用いた手法を比較した。100台までの小規模な問題ならハイブリッドソルバやシミュレーテッドアニーリングが大幅に最適化を行える手段だと分かった。しかし、大規模な問題はそもそもシミュレーテッドアニーリングでは解けず、ハイブリッドソルバも、ブラックファーストのアルゴリズムと同等の性能しか出せないことが分かった。全体として、ハイブリッドソルバや量子コンピュータ、シミュレーテッドアニーリングは産業上の問題を解決するための可能性を示せた。著者は、将来的には本研究で示された問題処理のボトルネックの解決や、さらなる量子アニーリングマシンによる最適化に適した対象の発見に努めるとしていた。

あとがき

今回の論文を読んで、車両の色を塗装する最適化の問題が存在することは初めて知り、それにより車の納期が短縮されるとしたら、現在のコロナ禍で起きている車両の製造の遅れの解決に寄与できるのではないかという可能性を感じながら読んでいた。するとこの論文では、塗装の１工程であるフィラーの塗装（二値のみ）についての最適化しか行っていなかった。しかし、このような簡単そうな問題であるにも関わらず、3000台の量の車の塗り方を最適化することもむずかしいということで、驚いた。私なら、この研究の発展として、ほかのデータセットでも同様の結果が出るのかを検証したいと考えた。また、白黒の二値のみではなく、何種類もの色を塗り分ける場合の効率化も考えてみたいと思った。

巻末資料

　本文中でイジングモデルのハミルトニアン$H_{MCPS}$中の$\lambda$について、$\lambda=N$として実験を行った。そこで、なぜ$N$が適しているのかを解説をする。

　まず、$H_{MCPS}$の前項$H_A$：

\begin{equation}
H_A =\,- \sum^{N-2}_{i=0} s_i s_{i+1}
\end{equation}

がすべて同じ向き($s_iがすべて+1または-1 $)のとき、最小値をとり、それは-(N-1)となる。

　次に、後の項$H_B$：

\begin{equation}
H_B=(\#C_l-2k(C_l))\sum_{i=0}^{M-1}s_i+\sum_{i<j\in A(C_l)}s_i s_j
\end{equation}

が制約項であることから、制約を破った場合は、$H_A$の最小値よりも大きな値を$H_B$が取らなければいけないので、$\lambda>N-1$となる$\lambda$として$N$を代入すると、$N-(N-1)=1>0$となるので、$\lambda$には$N$が適していることが分かった。

本記事の担当者

平間草太 (メンタリング：丸山尚貴、羽場廉一郎)