文献情報

• タイトル：Quantum-processor inspired machine learning in the biomedical sciences
• 著者：Richard Y. Li, Sharvari Gujja, Sweta R. Bajaj, Omar E. Gamel, Nicholas Cilfone, Jeffrey R. Gulcher, Daniel A. Lidar, Thomas W. Chittenden
• 書誌情報：Patterns 2(6), 2021, 10.1016/j.patter.2021.100246

概要

近年、コンピュータの高性能な処理能力を利用した高度なゲノム解析技術によって、複雑な分子レベルでヒト疾患の原因を解明する取り組みがなされています。その一方で、従来型のコンピュータやそれを利用したアルゴリズムの性能の頭打ちが近づいていることも事実です。そこで、本論文では近年進歩を続ける量子アニーリング技術を用いてガンデータの分類を行い、既存アルゴリズムとの比較評価を行います。量子アニーリングは、量子効果を用いてイジング模型の基底状態を探索します。このイジング模型の基底状態を古典的な計算によって探索することが可能なシミュレーテッドアニーリングの性能も評価します。その結果、イジング模型を用いた機械学習アルゴリズムは、学習データが少ない場合に優れた分類性能を持つことがわかりました。

方法

本論文では、下記の5つのガン細胞のペアについて2クラス分類を行います

• 淡明腎細胞がん (KIRC) vs. 乳頭状腎細胞がん (KIRP)
• 肺腺ガン (LUAD) vs. 肺扁平上皮ガン (LUSC)
• 浸潤性乳管ガン (BRCA) vs. 皮疹純正乳管ガン (normal)
• エストロゲン受容体陽性乳ガン (ERpos) vs. エストロゲン受容体陽性乳ガン (ERneg)
• ルミナルＡ乳ガン (LumA) vs. ルミナルＢ乳ガン (LumB)

これらに関するデータはThe Cancer Genome Atlas (TCGA) Dataから取得します。ガンを識別する際には、以下5種類の物質のデータを参考にします。

• messenger-RNA (mRNA)
• micro-RNA (miRNA)
• copy number variation (CNV)
• single nucleotide polymorphism
• DNA methylation

実験の概略図を図1に示します。5つの物質それぞれについて、各データの特徴ベクトルを行成分として持つ行列を生成し、それらを一つの行列に結合するこで、学習データを用意します。学習データのうち、80%を訓練データとし、20%をテストデータとします。訓練データには標準化を行います。この行列に対して主成分分析を用い、44個の特徴量に絞ります。

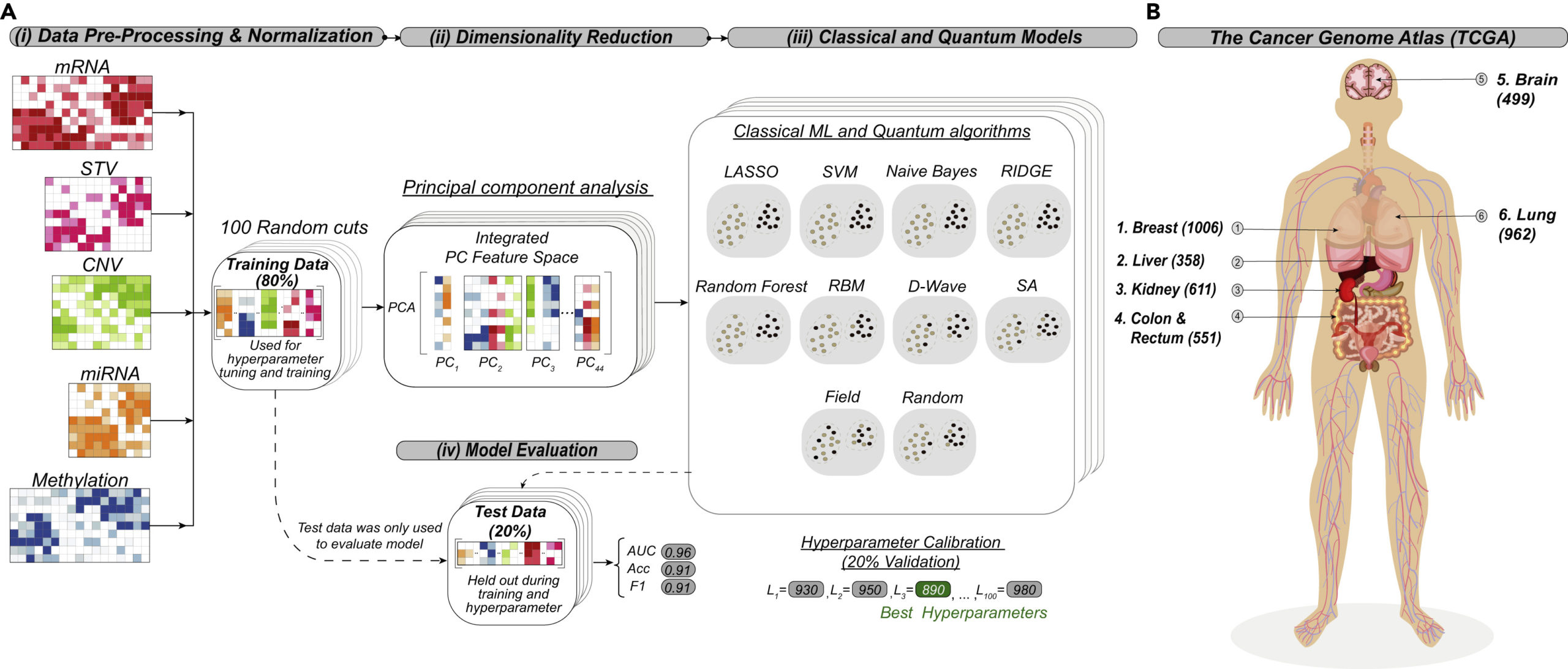
テストデータの分類は訓練データによって予め訓練された分類器によって行われます。本論文では10種類の分類モデルを作成します。分類モデルは、従来型の機械学習アルゴリズム用いる手法と、イジング模型を用いた手法に分けられます。

従来型アルゴリズム

• ラッソ回帰 (LASSO)
• リッジ回帰 (Ridge)
• ランダムフォレスト (Random Forest)
• 単純ベイズ (NB)
• サポートベクトルマシン (SVM)

イジング型アルゴリズム

• D-Wave（D-Wave Systems の D-Wave 2Xという量子アニーリングマシンを使用する）
• シミュレーテッドアニーリング (SA)
• Field
• Random
• 制限ボルツマンマシン(RBM)

これらのアルゴリズムについてを簡潔に説明します。

まず、LASSOは、次式で定義される、L1正則化線形回帰モデルです。

$$
\hat{\beta}({\lambda})=\min_{\beta}[-log[L(y;{\beta})]+{\lambda}|| {\beta} ||_1] \tag{1}
$$

また、Ridgeは、次式で定義される、L2正則化線形回帰モデルです。

$$
\hat{\beta}({\lambda})=\min_{\beta}[-log[L(y;{\beta})]+{\lambda}|| {\beta} ||_2^2] \tag{2}
$$

ただし、

$$
L= \frac{1}{N} \sum_{i=1}^{N}(y_i – {\beta}_0 – x_i {\cdot}{\beta})^2 \tag{3}
$$

であり、$\lambda \gt 0$ はモデルの複雑さを制御する正則化パラメータ、$\beta$ は回帰係数、$\beta_0$ はバイアス、$y$ はクラスラベル、$x_i$ は $i$ 番目の訓練サンプルを指します。学習の目的は、各式の量を最小にするような回帰係数 $\hat{\beta}$ を求めることです。予測ラベルは、$\hat{y} = \beta_0+x_i {\cdot}{\beta}$ で与えられます。

また、今回扱うSVMは、式(4)で定義されます。

$$
{\max_a}{L_D}(a) = \sum_{i=1}^{N}a_i  – \frac{1}{2}  \sum_{i,j=1}^{N}a_ia_jy_iy_jK(x_i,x_j) \tag{4}
$$

ただし、$L_D$は問題のラグランジュの双対性、$a_i$はラグランジュの未定乗数、$y_i, y_j$はi番目のラベルと訓練サンプル、$K(x_i, x_j)$はカーネル関数を表します。$ \sum_{i=1}^{N}{a_i}{y_i} = 0 $と${a_i}\geq{C}\geq{0} $の制約の元、最大値を捜索します。ここで、$C$は、非線形分類器における誤分類の度合いを制御するハイパーパラメータです。

イジング型アルゴリズムにおいては、ハミルトニアンが次式で表されるようなイジング模型として学習の目的関数を定義し、最適化を行うことで分類器の訓練を行います。

$$
H_p = \sum_{i}h_i{\sigma}_i + \sum_{i,j}J_{i.j}{\sigma}_i{\sigma}_j \tag{5}
$$

ただし、${\sigma}_i \in {-1, 1} $はスピン変数を表します。$h_i$局所磁場、$J_{i,j}$はスピン間の相互作用を表す定数です。

量子アニーリングは横磁場による量子ゆらぎを用いてエネルギーが最小となる解を探索します。今回はD-Wave Systemsが公開している、D-Wave 2Xという実機の量子アニーリングマシンを使用します。

今回論文では明記されていませんが、今回の2クラス分類の場合に当てはめてこれを考えます。例えば、一つ目の2クラス分類であるKIRC vs. KIRPでは、$\sigma=1$でサンプルがKIRCであった場合、$\sigma=-1$でサンプルがKIRPであった場合を指すとします。上で述べた、各行がサンプル、各列が遺伝子に当たる行列の分布と丁度重なるように、パラメータ$h_i$と$J_{i,j}$を返します。

さらに、SAは、同様に式(5)のイジング問題を受け取り、二値を返す計算器です。本来、イジングエネルギーが最小になるよう解を探索しますが、シミュレーテッドアニーリングでは、最適解を探す際に、基本的には値が小さくなる方向に探索しますが、その内確率$p$で、逆に値が大きくなる方向へ進みます。確率$p$は、最初は大きく、時間が経つにつれて小さくなるものとします。

Fieldでは、同様に式(5)で今度は$J_{i,j}$は無視し、訓練データを基にを求めます。最後に${\sigma_i}^{field} = -h_i$とします。

Randomでは、式(5)からランダムに解を生成します。各${\sigma}_i$にランダムに[0, 1)の範囲の値を与え、0.5以下のものは-1に、0.5以上のものは+1とします。

RBMは、可視層と隠れ層という二つの層から成る確率モデルです。入力分布を可視層に入力して学習を行い、学習パラメータが返されます。可視層の要素を$v_i$、隠れ層の要素を$h_j$とします。各要素のバイアスをそれぞれ$b_i, c_j$とします。隠れ層と可視層の間の結合の重みを$W_{i,j}$とすると、以下エネルギー関数

$$
E(v,h) = -\sum_i{b_i}{v_i} – \sum_j{c_j}{h_j} -\sum_i\sum_j{v_i}{W_{i,j}}{h_j} \tag{6}
$$

を用いて、RBMは式(7)のように定義されます。

$$
P(v,h) = \frac{\exp\{-E(v,h)\}}{Z(W)} \tag{7}
$$

ただし、Zは正則化係数です。式(7)の確率分布が入力データの分布に合うように、パラメータを調整します。

結果1｜ガン種類別の分類性能

これらの分類器を用いて前章で述べた5つの2クラス分類を行い、それぞれのアルゴリズムの精度を比較します。

訓練データとテストデータについて「正解率」、「不均衡データを考慮した正解率」、「AUC」、「F値」の4つの指標で分類器の精度を評価しました。各指標に関する詳細については補足の章を参照ください。訓練データとテストデータ100個の不均衡データを考慮した正解率を元に、順位を付けました。順位の高い順番に横軸に並べられています。

実験結果を図2に示します。

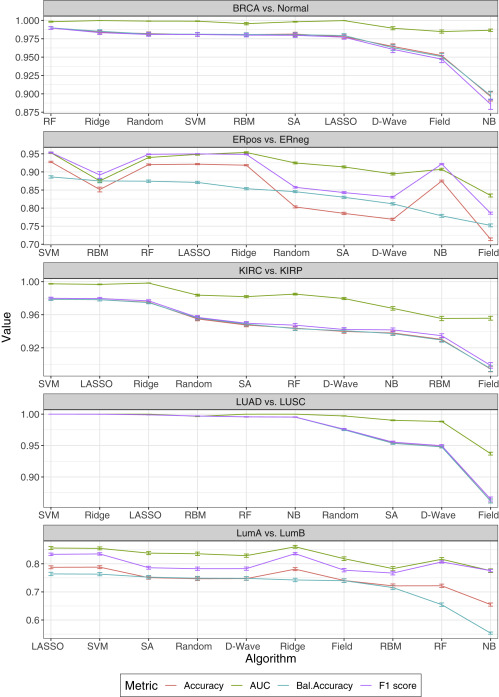
ERpos vs. ERnegの2クラス分類では、SVMの性能が最も良く、Fieldが最も悪いことが分かります。イジング型アルゴリズムに関しては、性能の高い順から、RBM2位、Random6位、SA7位、D-Wave8位、Field10位となっています。同じように、他の2クラス分類でも、イジング型アルゴリズムの順位はばらついており、機械学習アルゴリズムの方がやや性能が高い傾向にあります。

結果2｜学習データ数の依存性

さて、分類器の性能が、訓練データのサイズに依存することが先行研究で分かっています。そこで、訓練データのサイズを徐々に減少させ、訓練データサイズに対する各分類器の性能を評価します。本実験はLumA vs. LumBの2クラス分類で検証します。元々訓練データが250サンプルあるところを、最小50サンプル（元のデータサイズの20%）にまで減少させていきます。実験の結果を図3に示します。

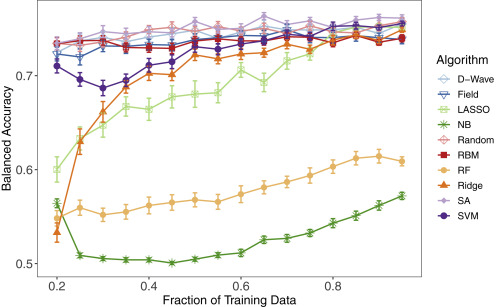
今回は、不均衡データを考慮した正解率に絞って示しています。訓練データサイズの減少に伴い、SVM、Ridge、LASSOの正解率は徐々に下がっています。RFやNBの正解率は一貫して他の分類器より低いままです。それに対し、残りのD-Wave、Field、Random、RBM、SAは概ね正解率が保たれています。具体的な数値を示すと、イジングモデルの性能は、訓練データサイズ95%で0.76、20%で0.73とほぼ下がらなく、LASSOでは0.75から0.60に下がりました。また、5つの機械学習分類器は全て過学習を起こしていました。

本結果によりイジング型アルゴリズムは少ないデータから重要な特報量を把握することができていたと言えます。式(5)で述べた通り、イジング型アルゴリズムは、イジングハミルトニアンのエネルギーが最小となる$\sigma_i$を探索するよう動作しますが、必ずしも最小のエネルギーとなる値を返すわけではありません。したがって、機械学習アルゴリズムほど分類の精度を重視しないため、過学習を起こさずに少量の訓練データでも性能を維持することができたと考えられます。

結論

以上のように、機械学習アルゴリズムとイジング型アルゴリズムを用いて、ガンの2クラス分類を行いました。その結果、データサイズの大きいデータに対しては、イジング型アルゴリズム分類器は機械学習アルゴリズムの分類器と同等、あるいはやや劣る性能を見せました。次に、訓練データサイズを減少させたところ、機械学習アルゴリズムは性能が減少したのに対し、イジング型アルゴリズムはほぼ一定の正解率を保ちました。この結果から、イジング型アルゴリズムは、データ量の限られているデータの分析に有用であると考えられます。

あとがき

機械学習や量子アニーリングの手法を実践的な内容で幅広く勉強することが出来ました。それぞれの分類器の長所や短所をより詳細に知りたいと思いました。それぞれのアルゴリズムによる具体的な分類方法の説明があればより分かりやすかったと思います。

本記事の担当者

田尻裕美子 (編集者：丸山尚貴、羽場廉一郎)

補足｜評価指標について

分類器の精度は、「正解率」、「不均衡データを考慮した正解率」、「AUC」、「F値」の4つの指標で評価しました。それぞれの説明を次に示します。機械学習の評価指標 分類編を参考にしています。

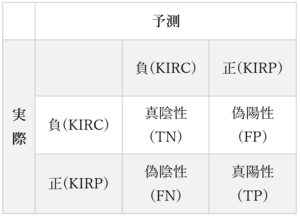
次のような混合行列を考えます。

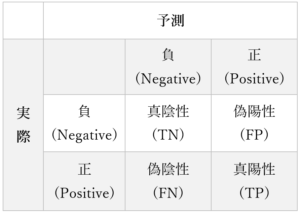
表１では、それぞれのマス目は次のことを示します。

• 真陰性(TN)：検査で陰性とされ、実際に陰性である場合
• 偽陰性(FN)：検査で陰性とされたものの、実際には陽性である場合
• 偽陽性(FP)：検査で陽性とされたものの、実際には陰性である場合
• 真陽性(TP)：検査で陽性とされ、実際に陽性である場合

なお、今回はガンの分類であるため、例えばKIRC vs. KIRPの2クラス分類では、混合行列は表２のようになります。

正解率は、式(8)で定義されます。

$$
\textrm{Accuracy} = \frac{TP+TN}{TP+FP+TN+FN} \tag{8}
$$

全予測の内、正解した予測の割合を指します。

また、今回扱うAUCは、ROC曲線下の面積の事を指します。ROC曲線は、横軸に偽陽性率、縦軸に再現率を取った曲線です。その曲線の下の面積は0から1の値を取り、その値が大きいほど良い予測が出来ています。

F値について、まず、適合率(Precision)と再現率(Recall)を定義すると、

$$
\textrm{Precision} = \frac{TP}{TP+FP} \tag{9}
$$

$$
\textrm{Recall} = \frac{TP}{TP+FN} \tag{10}
$$

です。適合率は、陽性と予測したもののうち、実際に陽性であるものの割合を表します。再現率は、実際に陽性であるもののうち、正しく陽性と予測されたものの割合を表します。これで、F値は、

$$
F-measure = \frac{2\times{Precision}\times{Recall}}{Precision+Recall} \tag{11}
$$

と定義されます。