概要
2022/06/22に開催されたAQC2022でポスター発表(オンライン)を行いました。本記事では、発表内容を日本語で解説します.
背景
皆さんは、温室効果ガス排出量の21.2%は自動車が原因であることをご存知でしょうか?
交通渋滞が発生し、自動車の速度が低下すると、温室効果ガスの排出量は増加します。渋滞を解消することは目的地に早く着けるだけでなく、環境にもやさしいのです。
目的
量子アニーリングを用いた信号機最適化の研究はいくつか存在します[1][2]。しかし、従来の目的関数は十字路かつ1車線のみを想定したものが多く、実際のマップに適応することが出来ません。そこで、T字路や複数車線にも対応可能な新しい目的関数を提案します。

[1]Inoue, D., Okada, A., Matsumori, T. et al. Traffic signal optimization on a square lattice with quantum annealing. Sci Rep 11, 3303 (2021). https://doi.org/10.1038/s41598-021-82740-0
[2]Hussain, H., Javaid, M.B., Khan, F.S. et al. Optimal control of traffic signals using quantum annealing. Quantum Inf Process 19, 312 (2020). https://doi.org/10.1007/s11128-020-02815-1
準備
それぞれの信号機が取りうる状態を「モード」と呼びます。
従来の手法では、モードは2つしかありませんでした。我々の手法では、交差点ごとにモードを定義する必要があります。
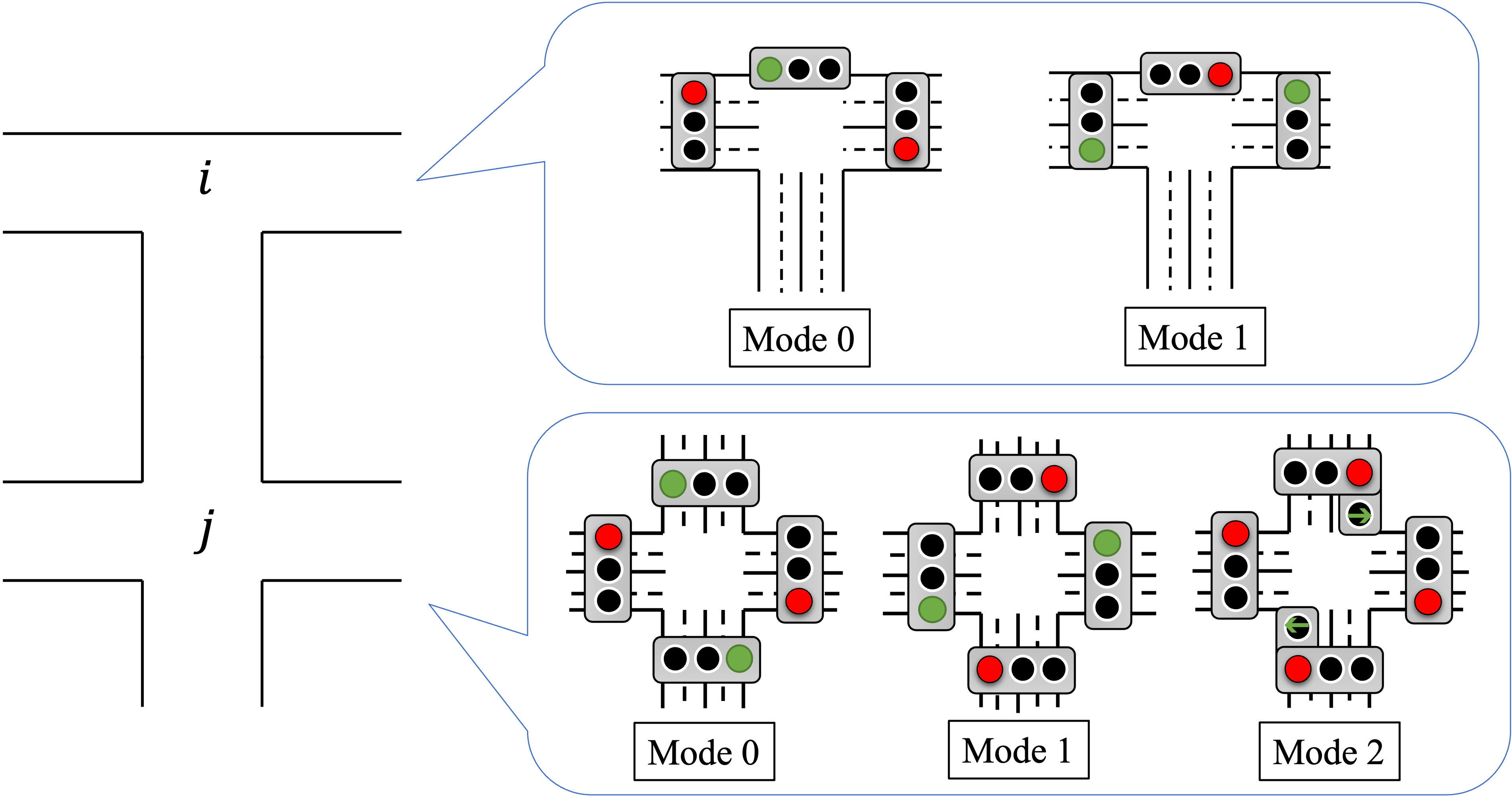
定式化
我々は、車両の「待ち時間」を削減するための目的関数を提案します。そのためには、「各交差点で通過できる車両の数」が最大となるモードを選べば良いでしょう。従って、1つ目の目的関数は次のようになります。
- バイナリ変数
$$
x_{i m}=\left\{\begin{array}{ll}
1 & \text { if i-th intersection takes m-th mode }\\
0 & \text { otherwise }
\end{array}\right.
$$
- 1つ目の目的関数
$$
\min H_{1}(X)=-\alpha \sum_{i} \sum_{m} C_{i m} x_{i m}
$$変数 説明 [latex]\alpha[/latex] ハイパーパラメータ 定数 説明 [latex]C_{im}[/latex] 交差点[latex]i[/latex]がモード[latex]m[/latex]を取る時に通過できる車両の数
ここで、[latex]C_{im}[/latex]について説明します。例として、次の交差点[latex]i[/latex]を考えてみましょう。
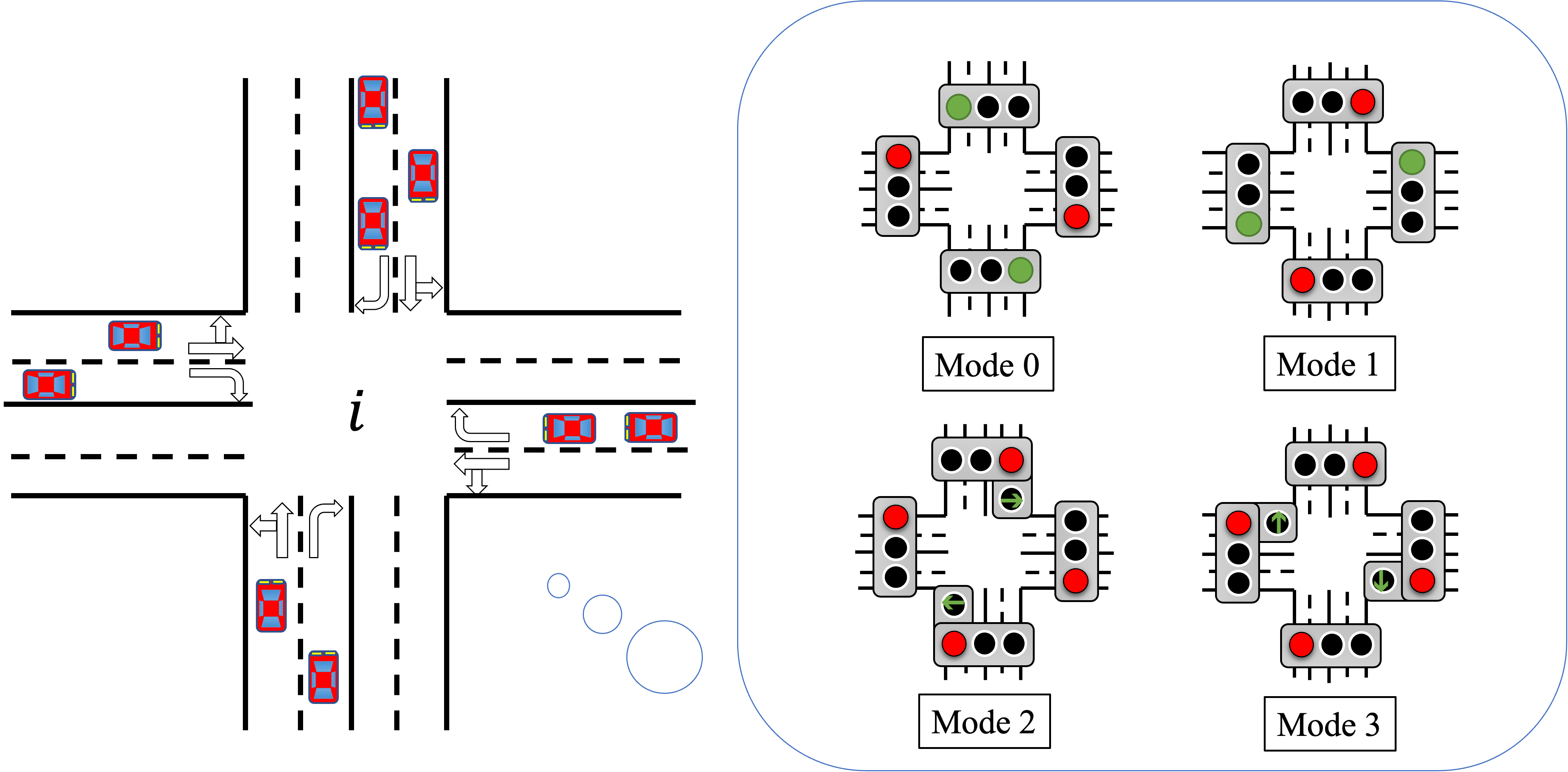
図のように、交差点[latex]i[/latex]は4つのモードを取ることが出来ます。それでは、モード0を取る場合から考えてみましょう。
モード0を取る場合
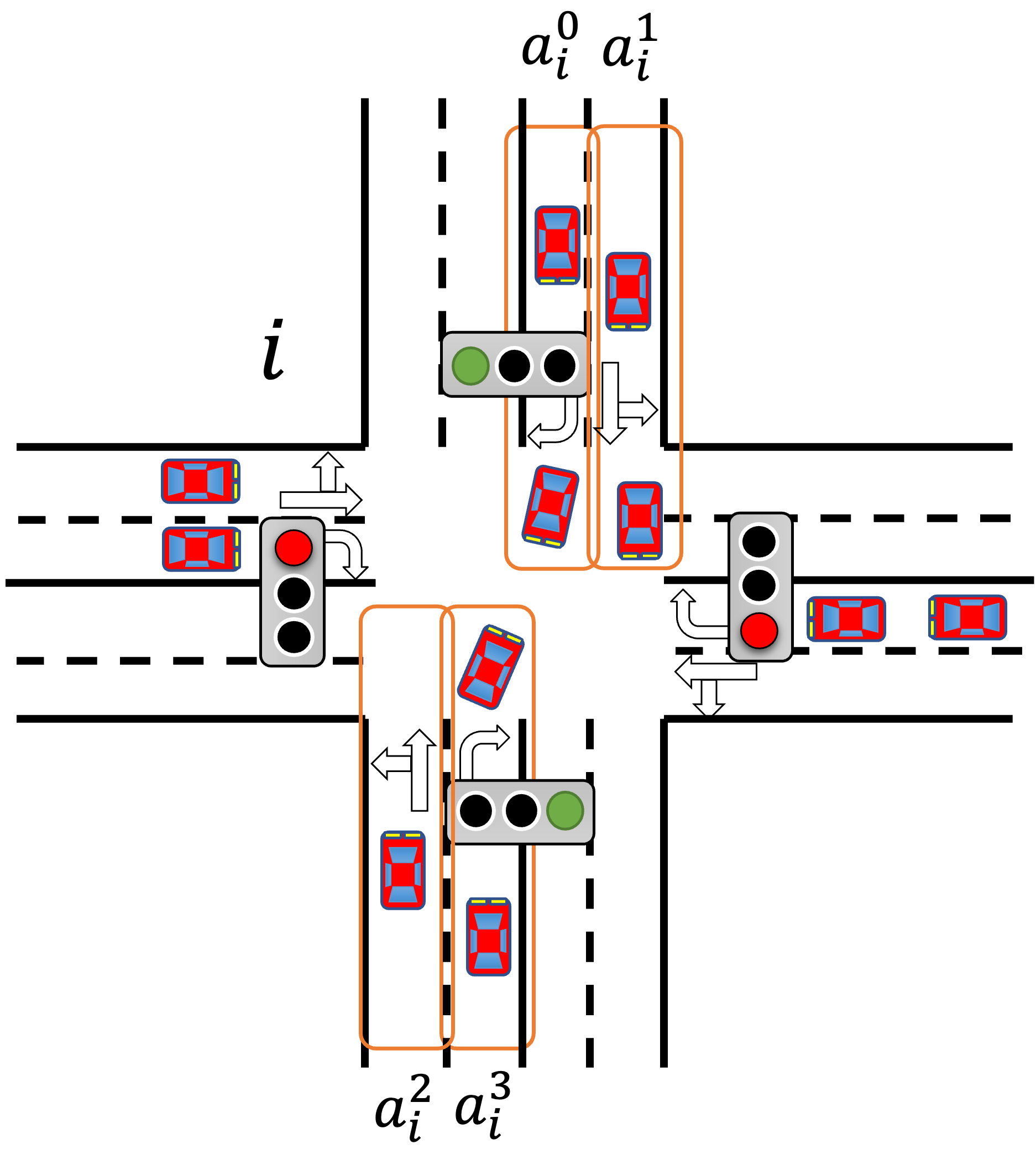
この場合、通過できる車両を単純に数えると、[latex]a_{i}^{0}+a_{i}^{1}+a_{i}^{2}+a_{i}^{3}[/latex]となります。しかし、右折車は対面する直進車を待つ必要があるため、左折-直進車よりも通過できる車両の数は少なくなります。そこで、[latex]C_{i0}[/latex]は次のように計算することにします。
$$C_{i0} := \lambda \times \left( a_{i}^{0}+a_{i}^{3}\right)+a_{i}^{1}+a_{i}^{2}$$
ここで、[latex]\lambda[/latex]は[latex]0<\lambda<1[/latex]の範囲で設定します。続いて、交差点[latex]i[/latex]がモード2を取る場合を考えましょう。
モード2を取る場合
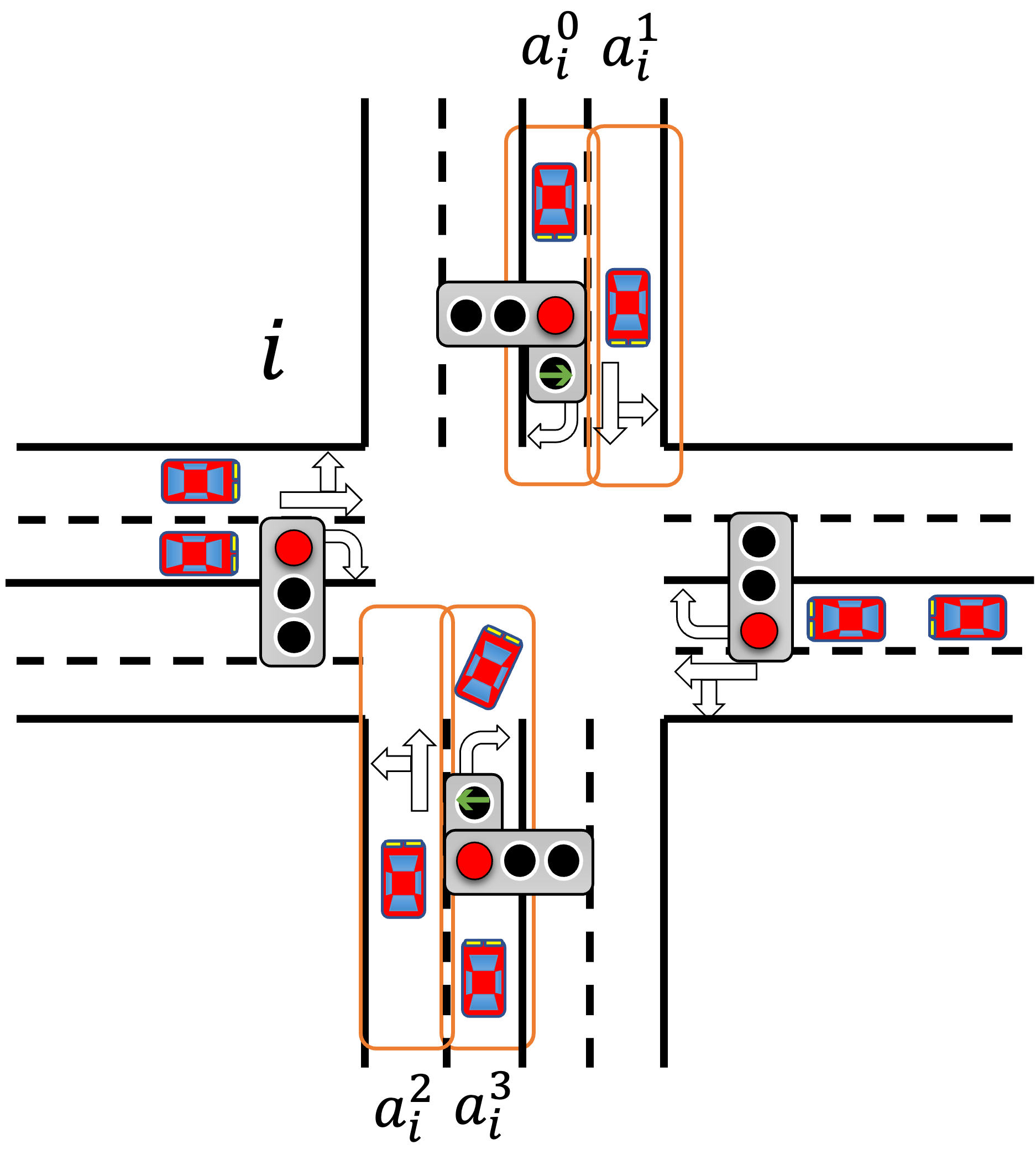
このモードでは、右折車のみが通過できるため[latex]\lambda[/latex]を導入する必要はありません。従って、[latex]C_{i2}[/latex]は次のように計算出来ます。
$$C_{i2} := a_{i}^{0}+a_{i}^{3}$$
他のモード1,3も同様に計算可能です。これで、[latex]C_{im}[/latex]の説明は終わりです。
1つ目の目的関数だけで「待ち時間」を削減出来るかというと、そうではありません。なぜなら、各交差点では最適なモードでも、次の交差点で停まってしまう可能性があるからです。
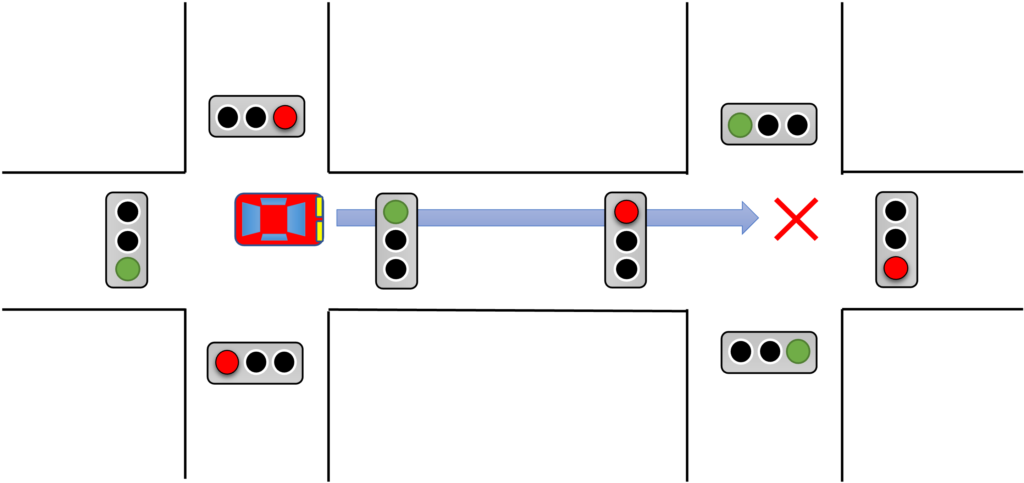
従って、次の交差点でも連続して通過できるように次の目的関数を導入しましょう。
- 2つ目の目的関数
$$
\min \quad H_{2}(X)=-\beta \sum_{i, m} \sum_{j \in N_{i}, n} B_{i j} R_{i m, j n} x_{i m} x_{j n}
$$変数 説明 [latex]\beta[/latex] ハイパーパラメータ [latex]n[/latex] 交差点[latex]j[/latex]の取りうるモード 定数 説明 [latex]N_{i}[/latex] 交差点[latex]i[/latex]に隣接する交差点の集合 [latex]B_{i j}[/latex] [latex]B_{i j}:=1/(平均到達時間)[/latex] [latex]R_{i m, j n}[/latex] [latex]i[/latex]が[latex]m[/latex]、[latex]j[/latex]が[latex]n[/latex]を取る時の関係性
まずは、[latex]R_{i m, j n}[/latex]について詳しく見ていきましょう。[latex]R_{i m, j n}[/latex]は、隣接する交差点の関係性を表しています。次の例が分かりやすいでしょう。
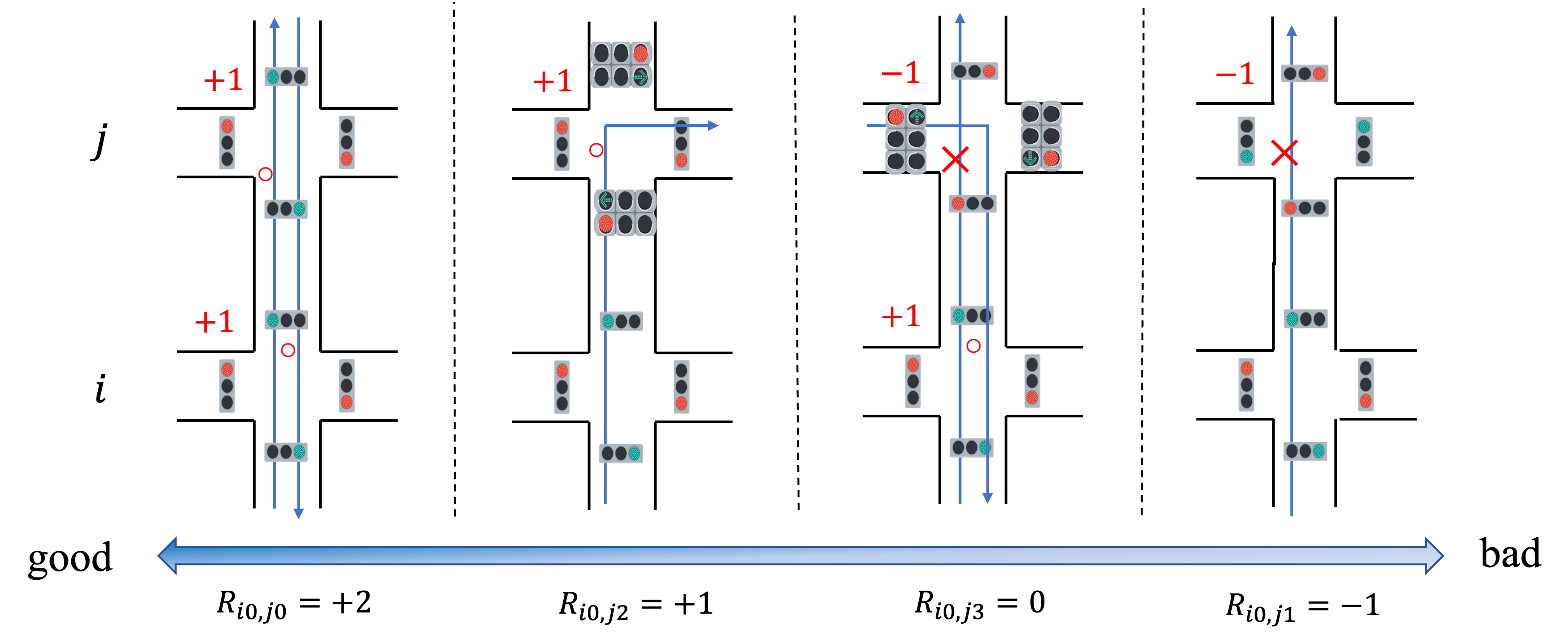
1番左の場合では、2方向が連続して通過できるため、ボーナスとして+2が与えられています。一方で、1番右の場合では、1方向が連続して通過できないため、ペナルティとして-1が与えられます。このように、隣接する交差点に相性を表すポイントを割り振るのが[latex]R_{i m, j n}[/latex]です。
続いて、[latex]B_{i j}:=1/(平均到達時間)[/latex]について説明します。平均到達時間は、「距離 / 制限速度」で求められます。これも、例を見るのが分かりやすいでしょう。
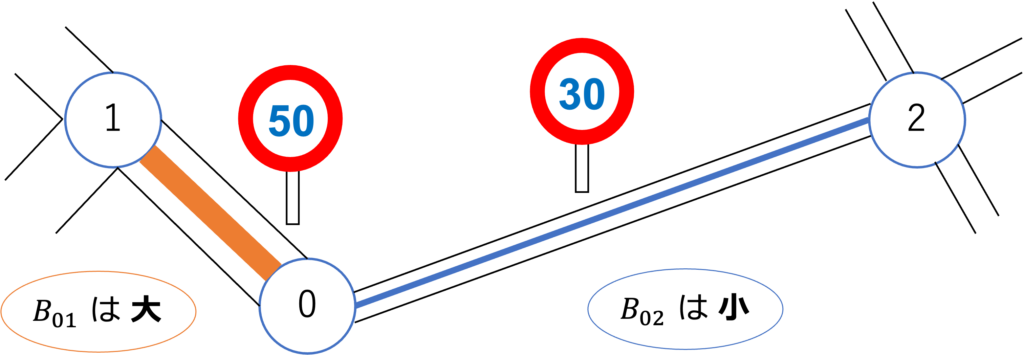
0-1間は、距離が短く、制限速度も速いです。従って、[latex]B_{01}[/latex]は大きい値になります。一方、0-2間は、距離が長く、制限速度も遅いです。従って、[latex]B_{02}[/latex]は小さい値になります。これより[latex]R_{i m, j n}[/latex]は、隣接する交差点の結合の強さ(Bond strength)を表していると言えます。
2つ目の目的関数についてまとめましょう。この目的関数の意味は、「結合の強い隣接する交差点で、相性の良いモードを選ぶ」です。
最後に、3つ目の目的関数を紹介します。これは、各交差点がモードを1つだけ取るようにするための制約です。
- 3つ目の目的関数
$$
\min \quad H_{3}(X)=\gamma \sum_{i}\left(\sum_{m} x_{i m}-1\right)^{2}
$$
[latex]\gamma[/latex]は、ハイパーパラメータです。
これで、全ての目的関数を紹介しました。最終的な目的関数は次のようになります。
$$
\begin{aligned}
& H_{1}(X)+H_{2}(X)+H_{3}(X) \\
=&-\alpha \sum_{i} \sum_{m} C_{i m} x_{i m}-\beta \sum_{i, m} \sum_{j \in N_{i}, n} R_{i m, j n} x_{i m} x_{j n}+\gamma \sum_{i}\left(\sum_{m} x_{i m}-1\right)^{2}
\end{aligned}
$$
実験
提案した目的関数を使用して実験を行いました。シミュレータはSUMO (Simulation of Urban MObility)を使用し、各車両の「待ち時間」を計測しました。実験の全体像は次の通りです。
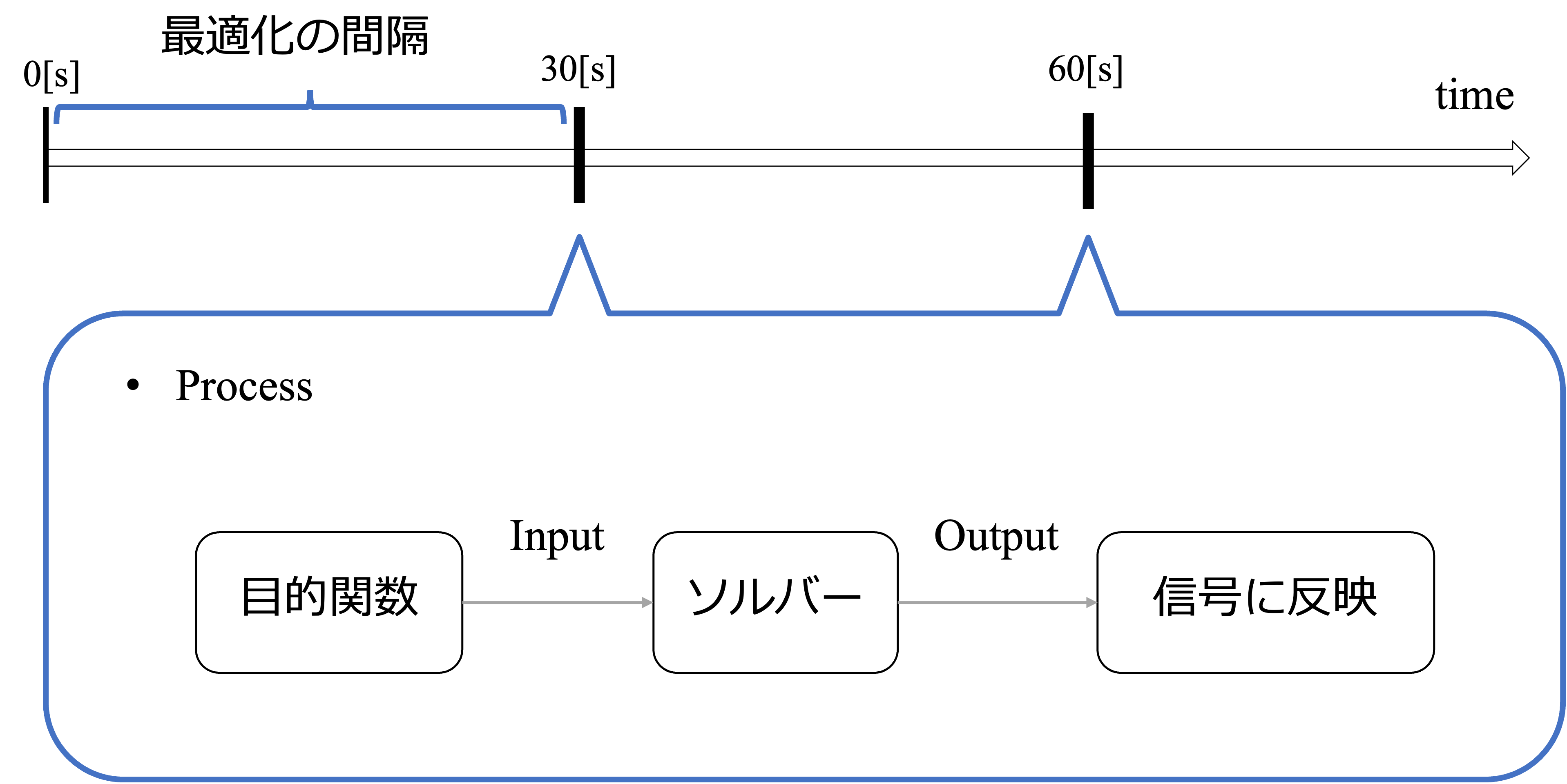
30[s]毎に、「Process」の内容を実行します。マップは仙台の一部を採用しました。
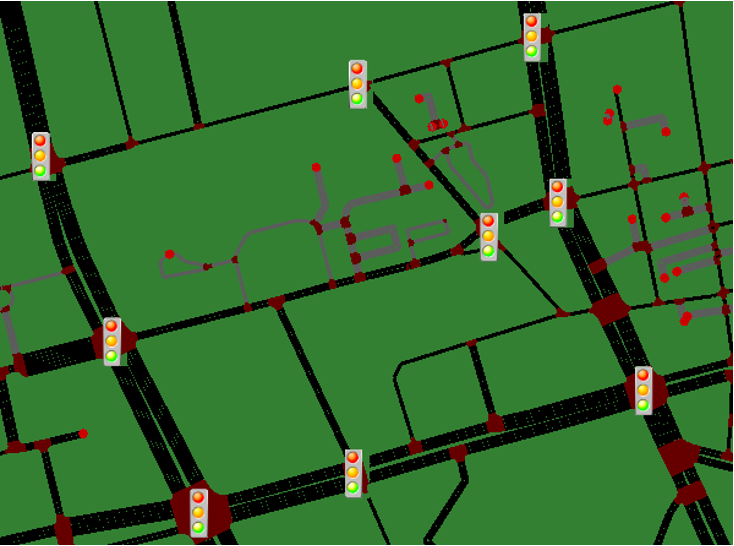
ご覧の通り、T字路や複数車線を含むマップになっています。その他の詳細な設定は、次の表を参照して下さい。
| 設定 | 値 |
|---|---|
| 実験の総時間 | 3000 [s] |
| 最適化の間隔 | 30 [s] |
| 交差点の数 | 9個 |
| 論理変数の数 | 23個 |
また、全ての実験で各車両の走行ルートは固定されています。
実験1
まずは、我々の目的関数で「待ち時間」を削減できるのか検証しました。そのために、30[s]毎にランダムに解を出力した場合と比較しました。
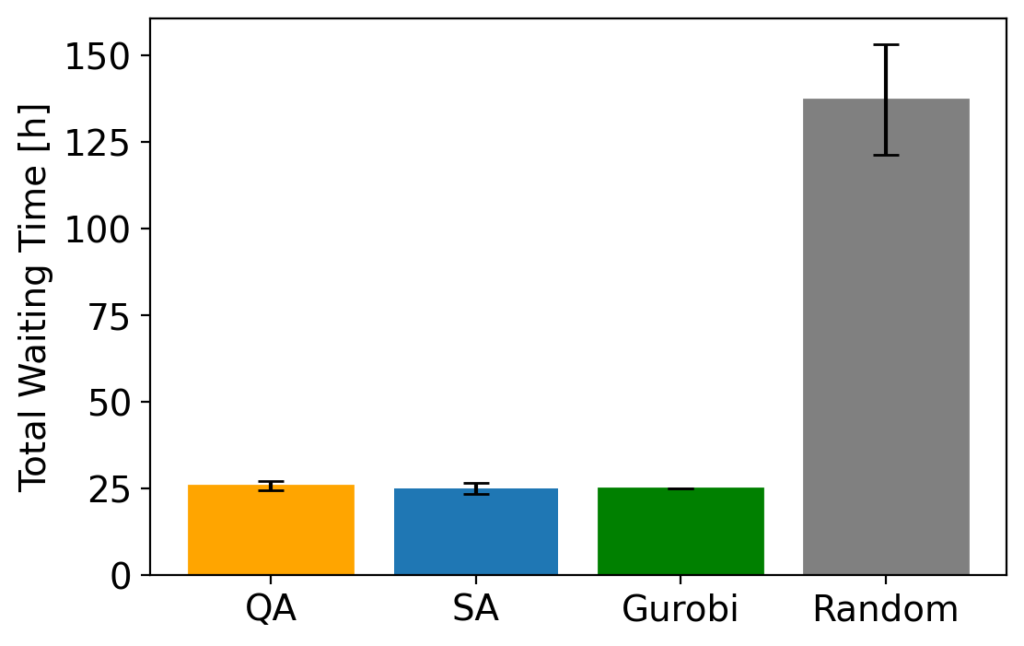
縦軸は「待ち時間」の総和、横軸はソルバーです。5回実験を行い、平均値をプロットしました。エラーバーは標準偏差です。
| ソルバー | 説明 |
|---|---|
| QA | D-Wave Advantage system 4.1 |
| SA | D-Wave SimulatedAnnealingSampler |
| Gurobi | 常に厳密解を出力する |
| Random | ランダムに解を出力する |
これより、我々の提案する目的関数で「待ち時間」を削減できることが分かりました。
実験2
続いて、既存の手法に比べてどれだけ「待ち時間」を削減出来ているのかを検証しました。既存の手法というのは、各モードで時間を固定し、このサイクルを繰り返すというものです。例えば、青信号の後に右折矢印に切り替わる信号機は、よく目にするのではないでしょうか。
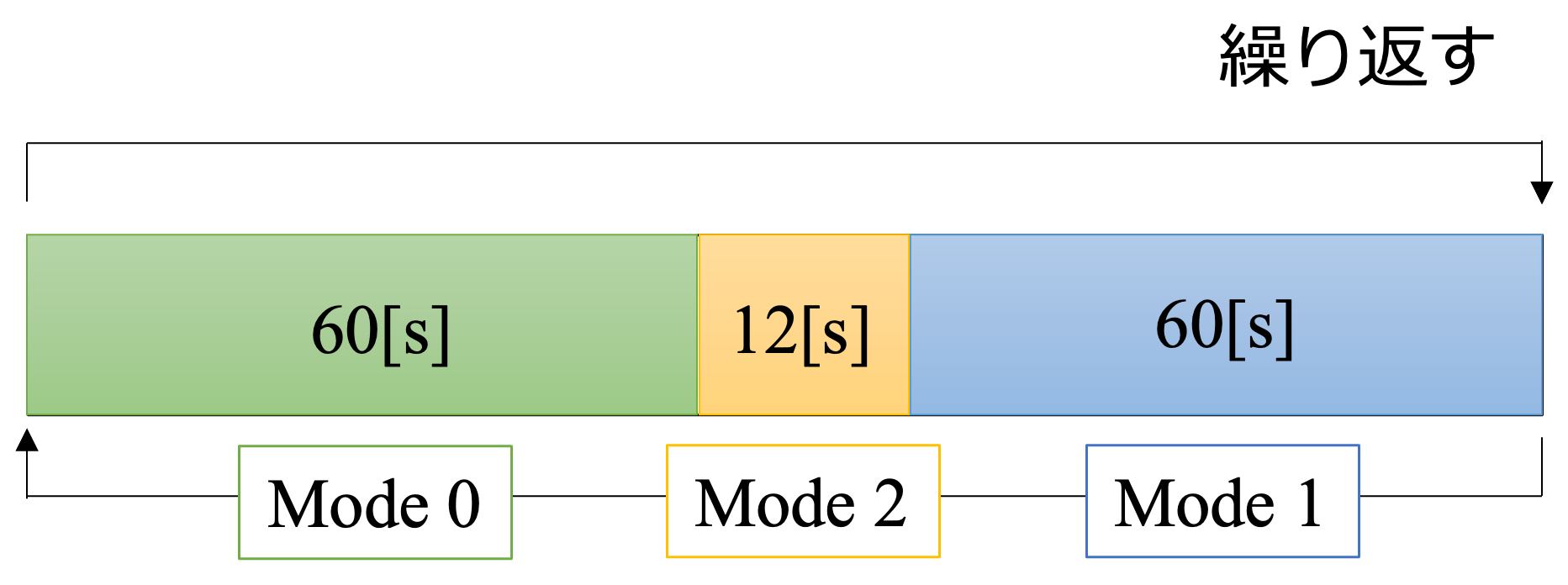
固定サイクルに対し、我々の手法では交通量によって柔軟にモードを切り替える事が可能になっています。それでは、比較結果を見てみましょう。
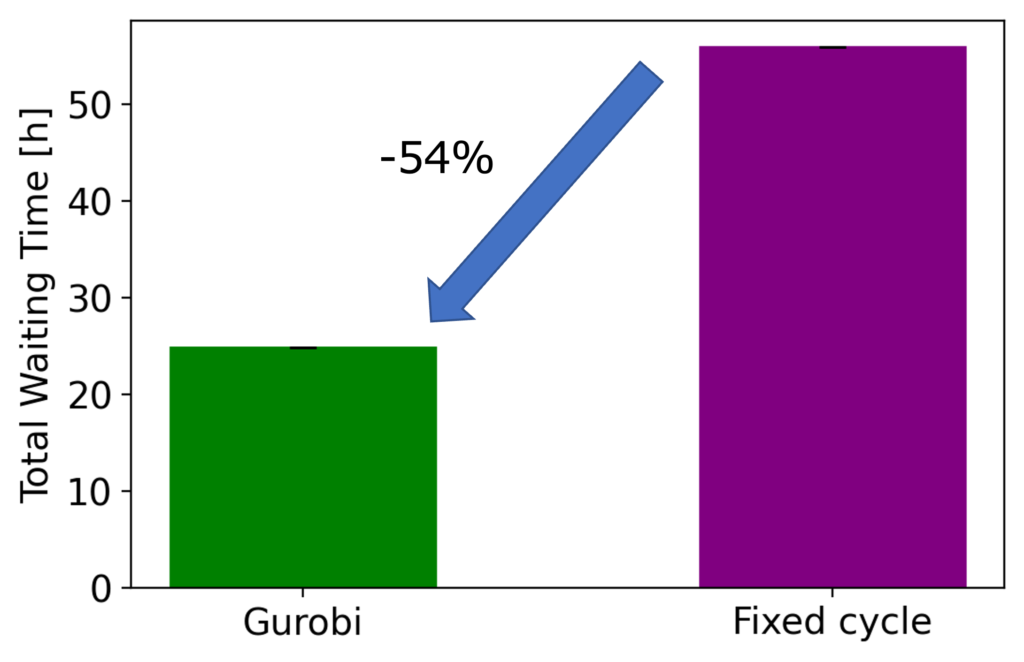
右の「Fixed cycle」は既存手法の結果を示しています。これより、既存手法に比べて「待ち時間」を約54%削減できることが分かりました。
実験3
これまで、マップ上全ての信号機を制御して実験を行ってきました。しかし、マップ上に存在する全ての信号機を同時に制御することは不可能です。そこで、制御する信号機の数を変化させて「待ち時間」の推移を観察しました。制御していない信号機は、固定サイクルで切り替わります。ソルバーはSAを使用しました。結果は次の通りです。
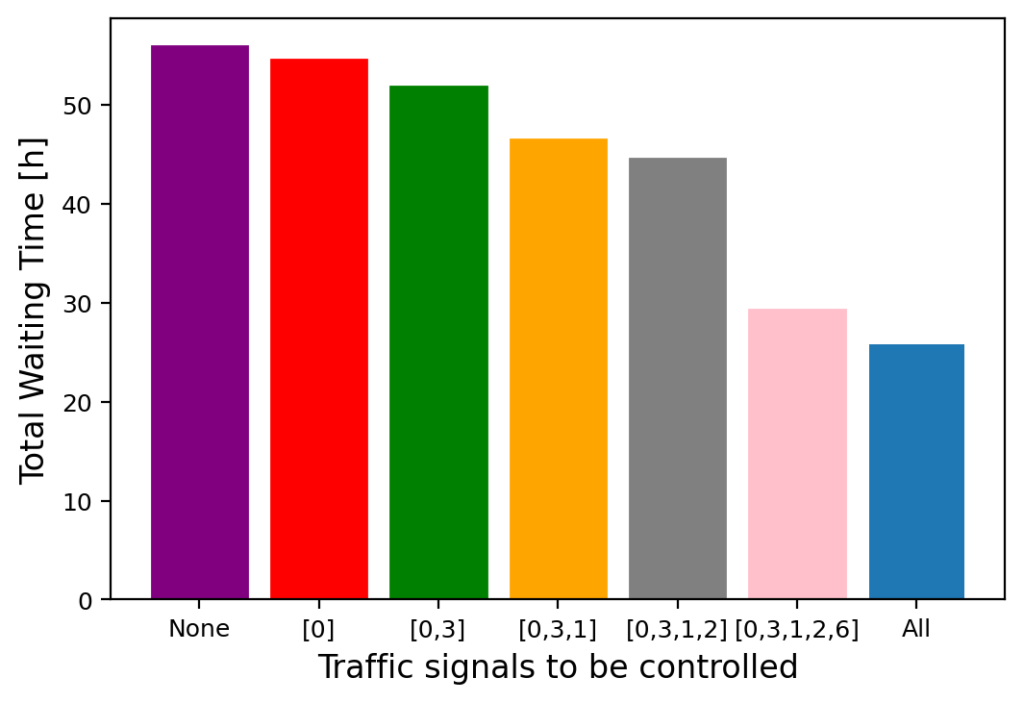
ここで、1番左の「None」は何も制御していないことを意味します。その右の[0]は制御した信号機のIDです。IDは、次のマップを参照して下さい。
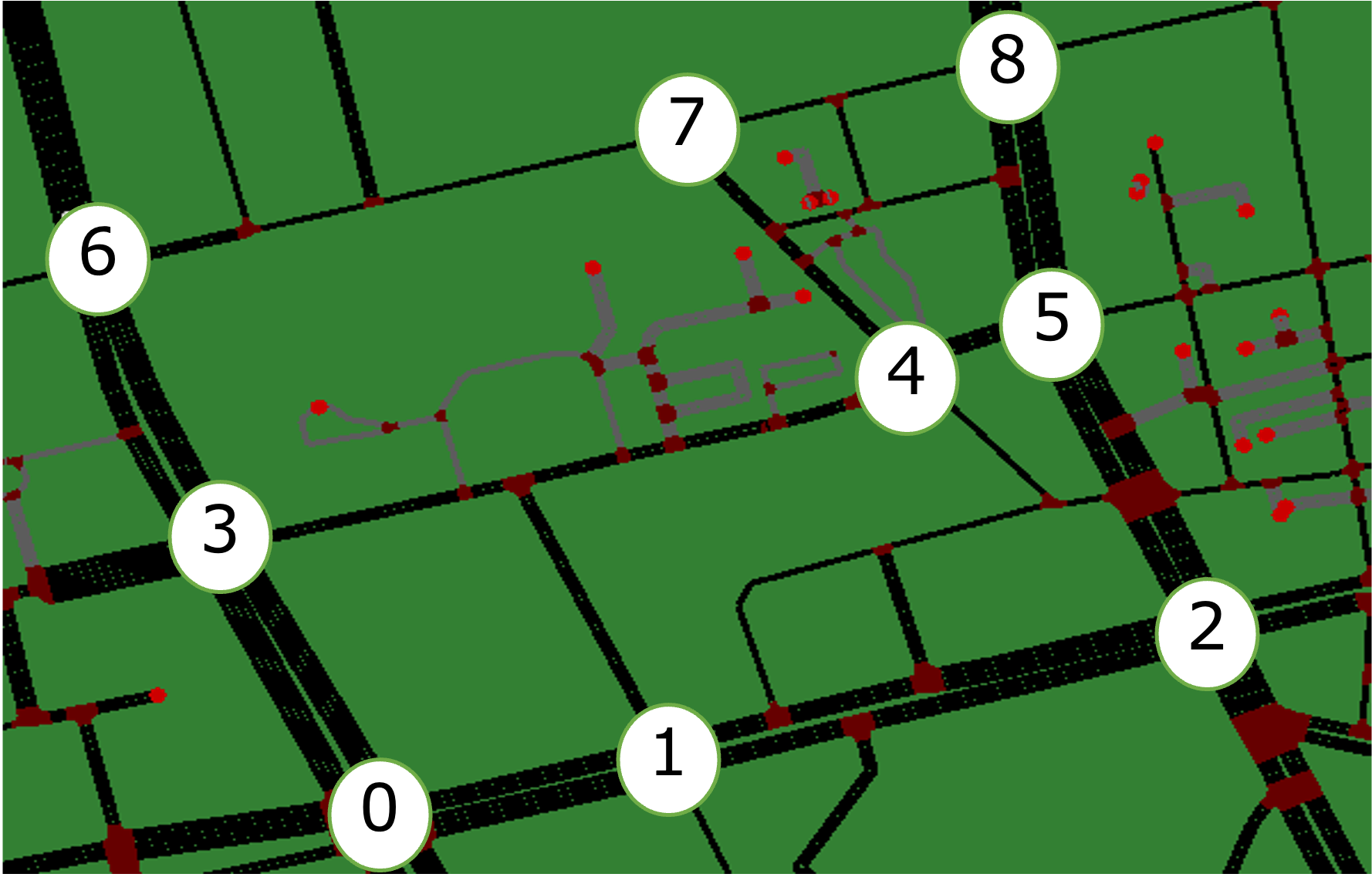
このように、制御する信号機の数を増やすほど「待ち時間」は減少していきます。これは自明のように思われますが、右から2番目の結果に注目して下さい。[6]を追加した途端、急激に「待ち時間」が減少しています。原因は不明ですが、より大きなマップで実験する際には、制御する信号機の組み合わせも重要になってくると考えられます。
考察
これまでの実験で、様々なソルバーを使用してきました。結局、どのソルバーを使うのが良いのでしょう?
今の所、QAかSAが最も適していると考えています。というのも,QAやSAがGurobiよりも「待ち時間」を削減することがあったからです(図11)。これは、厳密解が必ずしも最適解ではないこと、QAやSAが最適解以外にもいくつかの良質な解を出力していること、を意味しています。今後、どのような解が最も「待ち時間」を削減できるのか検証していきたいと考えています。
Q&A
最後に、よくある質問について回答します。
Q1. 問題サイズを大きくして実験しないのですか?
– SUMOの設定に時間がかかり、発表に間に合いませんでした。今後、サイズを大きくして実験していきます。
Q2. 既存手法の固定サイクルは、どのように決めたのですか?
– SUMOの自動生成アルゴリズムを使用しました。これがどれだけ信用できるのかは不明です。
Q3. どのソルバーで解くのが1番速かったですか?
– Gurobiが最速でした。ただ、問題サイズを大きくした場合、QAやSAが優位になるかもしれません。
補足
- パラメータの設定
パラメータ 値 α,β,γ 2.0, 1.0, 30 λ 0.3
- D-Waveマシンの設定
設定 値 solver D-Wave Advantage system 4.1 num_reads 1000 annealing_time 20[μs] anneal_schedule Default embedding D-WaveCliqueSampler
結論
本記事では、実際のマップに対応可能な新しいQUBOを提案しました。このQUBOを用いてシミュレーションを行ったところ、「待ち時間」を54%削減することが分かりました。しかし、マップ上に存在する全ての信号機を同時に制御することは不可能です。そこで、制御するもの、しないものがある場合に関しても実験を行いました。その結果、ある信号機の組み合わせで急激に「待ち時間」を減少できることが分かりました。これらの結果から、実際に量子アニーリングで信号機を制御する場合、どの信号機を制御するのかが重要になってくると考えられます。
あとがき
この信号機最適化は、「語義曖昧性の解消に量子アニーリングを用いる(記事作成中)」から発想を得ました。単語の持つ「語義」と信号機の「モード」。「隣接する単語間の関係性」と「隣接する交差点間の関係性」に似たものを感じ、定式化を行いました。この内容で論文を書けるように、これからも成果を出していきたいです。
また、当日は3名の方に発表する機会がありました。質疑応答で言語の壁を痛感したので、これからの英語学習のモチベーションにしていきたいと思います。
本記事の担当者
鹿内怜央