空港管制の発着ゲート割り当てを量子アニーリングで最適化するためには

文献情報

タイトル：Flight Gate Assignment with a Quantum Annealer
著者：Tobias Stollenwerk, Elisabeth Lobe, Martin Jung
書誌情報：https://doi.org/10.48550/arXiv.1811.09465

概要

航空機に対する発着ゲートの割り当ては航空管制において重要な業務の一つとなっています。この際、最も効率良いようなゲート割り当てを求めたいわけだが、これは組合せ最適化問題として扱うことができます。しかしながら、このような問題では最適解を高速に求めることが困難であることが知られています。したがって、本論文では量子アニーリングマシンのような新しいハードウェアの有用性を評価します。しかし、現実世界の問題では数多くの量子ビットを必要とするため、現状の量子アニーリングマシンでそのまま計算を行うことはできません。そこで、問題の構造を維持したまま、データを前処理することで、量子ビットを削減することを試みました。

問題

現代の空港管理においては、乗客、航空機を含めた全体的な動きの管理が求められています。そのうちの一つとして、航空機に対する適切な発着ゲートの割り当てがあげられます。しかし、この問題は二次割り当ての問題に該当し、現実的な時間で最適解を求めることが難しいとされる問題に該当します。そこで、この問題に対して量子アニーリングマシンのような新しいハードウェアの有用性を評価します。次章では量子アニーリングマシンでゲート割り当て問題を扱う手法を説明します。

方法

量子アニーリングマシンは、QUBOと呼ばれる形式の最適化を計算することができます。本章では、ゲート割り当て問題をQUBOとして表現する方法を説明します。

定義

まず初めに乗客を

出発
到着
乗り換え

の３つのグループに分け、それぞれのグループに対して以下の図１のような定数を設定します。

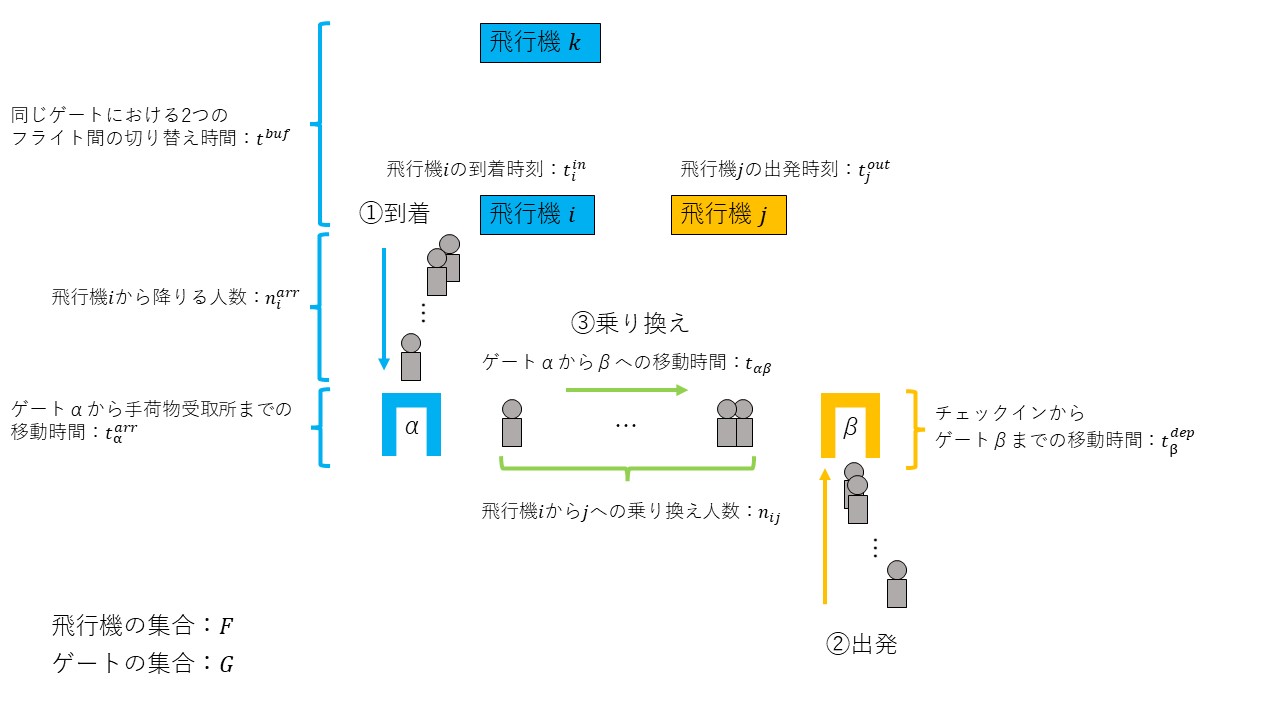
次に、どの航空機をどのゲートに割り当てるかを表す二値変数を定義します。

$$
\begin{equation} x_{i\alpha} = \begin{cases} 1 & \text{(航空機$i$($\in F$)をゲート$\alpha$($\in G$)に割り当てる場合)} \\ 0 & \text{(その他の場合)} \end{cases} \end{equation}
$$

これらの定数と変数を用いてQUBOと呼ばれる形式で定式化を行います。QUBO形式では以下の式で表されるような二値変数xの二次関数を最小化します。

$$
\begin{equation}
q(x) = x^TQx = \sum_{j=1}^{n}Q_{jj}x_j + \sum_{j,k=1,j<k}^{n}Q_{jk}x_jx_k
\end{equation}
$$

QUBO

今回定義するQUBOは目的関数と制約項の和で表されます。目的関数は問題を解く上で最小化したい値を表します。一方、制約項は問題を解く上で満たさなければならない条件を違反する場合に追加のエネルギーを課すためのものです。以下ではその二つについて定式化を行います。

目的関数

定義で述べたように乗客を３つのグループに分けたため、目的関数も同様の分け方をします。まず 1.出発 2.到着のグループについて、これらのグループの乗降時間は次式で表されます。

\begin{equation} T^{arr/dep}(x) = \sum_{i\alpha}n^{arr/dep}_it^{arr/dep}_\alpha x_{i\alpha} \end{equation}

次に 3.乗り継ぎのグループの乗降時間は次式で表されます。

\begin{equation} T^{trans}(x) = \sum_{i\alpha j\beta}n_{ij}t_{\alpha \beta}x_{i\alpha}x_{i\beta} \end{equation}

すべての乗客の乗り換え時間はこれからのグループの移動時間の総和で表され、目的関数は次式のように表されます。

\begin{equation} T(x)=T^{arr}(x)+T^{dep}+T^{trans}(x) \end{equation}

制約条件

本論文の最適化問題を解く上では次の二つの制約が存在します。

各航空機はただ1つのゲートに割り当てられる。
各ゲートにはちょうど1台の航空機が割り当てられる。

まず制約1.について、以下のように定式化します。

\begin{equation} C^{one}(x)=\sum_i(\sum_\alpha x_{i\alpha}-1)^2 \begin{cases} >0 & \text{(制約が満たされていない場合)} \\ =0 & \text{(制約が満たされている場合)} \end{cases} \end{equation}

本論文では制約項の強さを$\lambda$を用いて調節します。制約項の中で制約1.は以下のように表されます。

\begin{equation} \lambda ^{one}C^{one}(x) \end{equation}

次に制約2. について、以下のように定式化します。

\begin{equation} C^{not}(x) = \sum_\alpha \sum_{(i,j)\in P}x_{i\alpha}x_{i\beta} \begin{cases} >0 & \text{(制約が満たされていない場合)} \\ =0 & \text{(制約が満たされている場合)} \end{cases} \end{equation}

ただし上式における$P$は、航空機$j$への乗客の乗り込み時間が、航空機$i$への乗客の乗り込み時間より長く、航空機から降りる時間とそのゲートの切り替え時間の和よりも短い2機の航空機の組の集合を表します。

\begin{equation} P = \lbrace (i,j)\in\mathbb{F}, t_i^{in}<t_j^{in}<t_i^{out}+t^{buf}\rbrace \end{equation}

よって制約2.は制約1.同様以下のように表されます。

\begin{equation} \lambda^{not}C^{not}(x) \end{equation}

それぞれの制約条件の係数は制約項の強さを決定するものです。続いて、その係数の決め方を説明します。

まず制約項1. のパラメータについて

と設定したとき、

\begin{equation} \lambda^{one} = T^{one} + \varepsilon \quad(\varepsilon > 0) \end{equation}

としました。これによって航空機が複数のゲートに重複した場合、余分でかつ問題内で最も重いペナルティが発生するようになります。
次に制約項2. のパラメータについて

\begin{equation} T^{not} = max_{i,\alpha,\gamma} \Big( (n_i^{dep}t_\alpha^{dep} + n_i^{arr}t_\alpha^{arr} + max_\beta t_{\alpha\beta}\sum_j n_{ijk}) -(n_i^{dep}t_\gamma^{dep} + n_i^{arr}t_\gamma^{arr} + max_\beta t_{\beta\gamma}\sum_j n_{ij}) \Big) \end{equation}

と設定したとき

\begin{equation} \lambda^{not} = T^{not} + \varepsilon \quad(\varepsilon > 0) \end{equation}

としました。これによってある航空機についてのゲート占有時間を比較することで、乗客の最悪移動時間が大きいものを利用した場合、重いペナルティが発生するようになります。

QUBOの定式化

上記の目的関数と制約項を用いてQUBOは次のように表されます。

\begin{equation} q(x) = T(x) + \lambda^{one}C^{one}(x) + \lambda^{not}C^{not}(x) \end{equation}

データセット

データ$L_{CC}$として、航空機が3-16機、ゲートが2-16台の163個のデータセットを用意しました。ここで、それぞれの航空機間では乗客の乗り継ぎが必ず存在しています。なお、乗客の人数はドイツのある空港のデータ、乗客の移動時間は別のシミュレーション結果に基づいたものをアニーリングマシンで計算できるように加工しています。

次にデータ$L_{CC}$を簡略化するために乗客の人数を$\{ 0,1,\cdots,N_p \} $（ただし$N_p = \{ 2,3,6,10 \} $）個グループに分け、さらに乗客の移動時間に$\{1,\cdots,N_t \}$（ただし$N_t = \{2,3,6,10 \}$）のうちの適当な数値を割り当て、データ$L_{BP}$としました。ここで$L_{CC}$のデータの目的関数$T(\boldsymbol{x})$に対する$L_{BP}$とのデータの目的関数$T(\widehat{\boldsymbol{x}})$の比

\begin{equation} R = \frac{T(\boldsymbol{x})}{T(\boldsymbol{\widehat{x}})} \end{equation}

を考えます。R=1に近いほどデータL_CCからデータL_BPへの加工操作の影響は小さいことを表します。その結果を以下の図に示します。

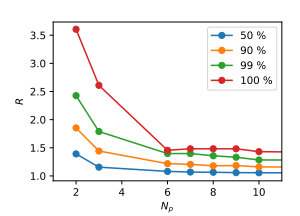
図2. $N_p$とデータ加工前後の目的関数の比（https://doi.org/10.48550/arXiv.1811.09465）
ただし各線は163個のデータのうち、近似率$R$の低い順から50,90,99,100%のデータの平均の推移を表しています。

計算結果の評価

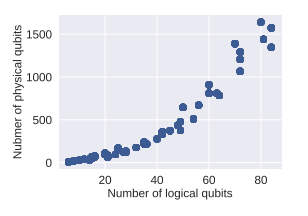
図3. データセットに対する論理量子ビットと物理量子ビットの関係（https://doi.org/10.48550/arXiv.1811.09465）

用意したデータセットに対して、（図3）のように量子アニーリングマシンで用いる物理量子ビット数は論理量子ビット数の増加に従います。ここで論理量子ビットとは問題を扱う際に必要となる計算上の量子ビットを表し、物理量子ビットとは論理量子ビットを実現するために必要な実際の量子ビットを指します。

前項におけるQUBOで乗客の最悪移動時間を用いて求めたQUBO行列が、計算に必要な最小のQUBOに対してどれほど差があるかを以下の式を用いて評価します。

\begin{equation} C_{QUBO} = \frac{max_{ij}|Q_{ij}|}{min_{ij}|Q_{ij}|} \end{equation}

そして、その各データに対応するイジングモデルの最大係数比

\begin{equation} C_{Ising}=max \biggl\{ \frac{max_i |h_{ij}|}{min_i |h_{ij}|}, \frac{max_{ij} |J_{ij}|}{min_{ij} |J_{ij}|} \biggr\} \end{equation}

を設定しました。

これらを用意したデータセットに対して用いると、論理量子ビットの増加ととも$C_{QUBO}$、$C_{Ising}$のどちらも増加しました。問題サイズが大きくなると物理量子ビット間の相互作用を高階調数で表現する必要があるため、現在の量子アニーリングマシンでは解くことができません。したがって、データを簡略化する処理であるデータ$L_{CC}$からデータ$L_{BP}$への加工を行いました。

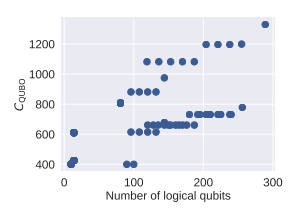
図4. データセットに対する論理量子ビットと$C_{QUBO}$の関係（https://doi.org/10.48550/arXiv.1811.09465）

さらに、厳密解に対する99%の精度で解を求めるまでの時間$T_{99}$を次式のようにして求めます。

\begin{equation} T_{99} = \frac{\ln(1-0.99)}{\ln(1-p)}T_{anneal} \end{equation}

$T_{anneal}$は量子アニーリングマシンの計算時間、$p$は厳密解に対する解の精度を表します。

以降の実験では量子アニーリングマシンの計算時間を$T_{anneal} = 20 \mu s$と設定しました。

結果

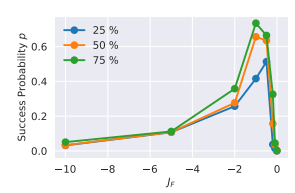
図5. $L_{BP}$における内部の量子ビットの結合$J_F$に対する厳密解に対する解の精度（https://doi.org/10.48550/arXiv.1811.09465）
ただし各線は厳密解に対する精度$p$の低い順から35,50,75%のデータの平均を表しています。

図5に示すように、内部の論理量子ビットの結合J_Fに対する解の精度は$J_F = -1$の時、最も高いことがわかります。これは$J_F$が大きい場合はD-waveマシンに対して高い階調度が要求されてしまい、マシンの階調度以上の制度が要求されてしまうためと考えられます。また、$J_F$が小さい場合は、論理量子ビットのつながりが切れてしまうため精度が下がってしまいます。
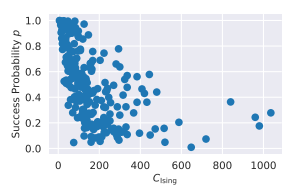
さらに下図に示すように、$C_{Ising}$が大きくなるにつれて解の精度は減少することがわかります。これは$C_{Ising}$の増加とともに高い精度が要求されることによります。

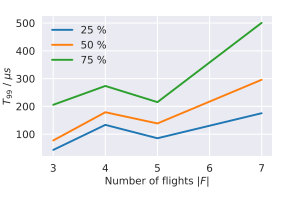
図6. $J_F = -1$とした時の$L_{BP}$における$C_{Ising}$と最も良い解の精度の関係（https://doi.org/10.48550/arXiv.1811.09465）

図7. $L_{BP}$におけるフライト数に対する$T_{99}$（https://doi.org/10.48550/arXiv.1811.09465) ただし各線は$T_{99}$の低い順から35,50,75%のデータの平均の推移を表しています。

　上図ではフライト数|F|に対する解を求めるまでの時間の関係を示しており、フライト数の増加に伴い、解を求めるまでの時間が増加していることがわかります。これはフライト数の増加によって問題サイズが大きくなっていることに起因しており、このことは下図の$C_{Ising}$の増加によって説明されます。

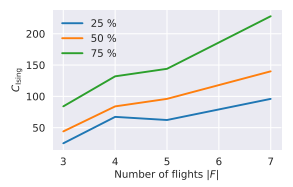
図8. $L_{BP}$におけるフライト数に対する$C_{Ising}$（https://doi.org/10.48550/arXiv.1811.09465）
ただし各線は$C_{Ising}$の小さい順から35,50,75%のデータの平均の推移を表しています。

結論

以上の実験から、ゲート割り当て問題はデータに対して前処理を施すことによってアニーリングマシンによって解くことができました。しかしながら、全ての場合でアニーリングマシンで解くことができるわけではありませんでした。まず、計算の際にアニーリングマシンが処理できる以上の量子ビット同士の結合を必要とする問題では解くことができませんでした。また、現実の問題を用いた場合はアニーリングマシンの階調度以上の精度が要求され、解を求めることができませんでした。二つ目の問題に対しては、本論文で行ったように$L_{CC}$から$L_{BP}$にデータを変換することでデータの類似度を失うことなくこの問題を解決することができました。

あとがき

この論文をまとめるにあたっては何度も挫折を繰り返し、長い時間をかけてしまいました。その理由としては二つの点が挙げられます。まず元の論文には結論を導くまでにデータの加工の正当性を示す過程が存在し、この理解が私にとっては難解であったためです。次に、問題の結論に対して私が過剰な期待を持っていたことが挙げられます。この論文の結論はゲート割り当て問題をアニーリングマシンによって最適化問題として解くことができるということでした。私は当初、この問題に対してアニーリングマシンが劇的な変化をもたらすものだと想像していました。しかし実際に読み進めていくうちに、そこには予想以上に淡白な結果が示されており困惑してしまいました。今回は空港を例としてあるゲートの通過時間とゲート間の移動時間が最小になるような解を求める問題でしたが、一般化することでほかにも応用先があるのではないかと感じました。

Post Views: 357