クリーク被覆問題をD-Waveマシンで解く

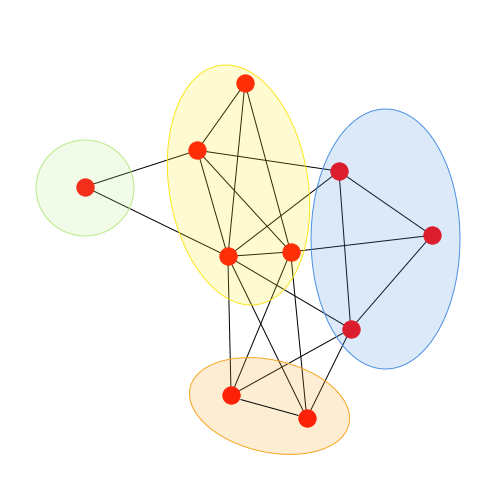
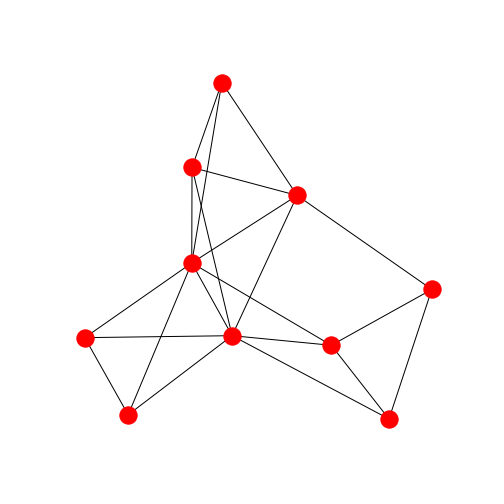
Karpの21のNP完全問題の一つであるクリーク被覆問題 (Clique Cover Problem)を、D-Wave 2000Qを用いて解いた。クリーク被覆問題のQUBO表現による定式化を解説したのち、Python SAPIを介したD-Waveマシンの実装例とその実行結果を紹介する。

クリーク被覆問題とは

クリーク被覆問題の導入

クリーク被覆問題 (Clique Cover Problem)とは、あるグラフ$G=\left(V,E\right)$と$n$種類の色が与えられたとき、そのグラフを$n$個のクリークに分割できるかを決定する問題である。特に、与えられたグラフの頂点をすべて含むようなクリークの集合を考える問題をクリーク頂点被覆問題(Clique Vertex Cover Problem)、与えられたグラフの辺をすべて含むようなクリークの集合を考える問題をクリーク辺被覆問題(Clique Edge Cover Problem)という。

与えられた頂点集合を$n$個に分割した各集合がクリークか否かの判定は、多項式時間でできるのでこの問題はNPに属する。NP完全性は、グラフの$n$彩色可能性から帰着され、グラフ$G$の$n$個のクリークへの分割は、補グラフ$G’$の$n$個の独立集合への分割に対応する。

QUBO表現による問題の定式化

組合せ最適化問題の種類: 彩色問題(Coloring Problem)
変数: $x_{v,i} \in \{0, 1\}$ (頂点$v \in V$が色$i \in \{1, 2, \cdots, n\}$で塗られる場合$1$, そうでなければ$0$)
目的関数:

$$ H = A \sum_{v} \left( 1- \sum_{i=1}^n x_{v,i} \right)^2 + B \sum_{i=1}^n \left[ \frac{1}{2}\left(-1+\sum_v x_{v,i}\right)\sum_v x_{v,i} – \sum_{(u,v) \in E} x_{u,i} x_{v,i} \right] $$

目的関数の第1項は、各頂点に1色のみ割り当てるための制約条件によるものである。第2項は、分割した部分グラフがクリーク、つまり完全グラフにどれほど近いかを表すコスト関数である。すべての部分グラフがクリークである場合に限り、第2項は0となる。

QUBO行列を生成するPythonコード

上記の定式化したイジング模型をPythonにより実装したコードを、以下に示す。

# 頂点の数
N_VER = 16

# 色の数
N_COLOR = 5

# イジング変数の数
N = N_VER * N_COLOR

# h(局所磁場), J(相互作用の係数), S(隣接行列)
h = [0] * N
J = {}
S = {}

# 一つの頂点に一色だけ割り当てる
A = 1
for v in range(N_VER):
    for i in range(N_COLOR):
        h[v*N_COLOR+i] = -A
        
        for j in range(i+1, N_COLOR):
            J[v*N_COLOR+i, v*N_COLOR+j] = 2 * A

# クリークにどれだけ近い構造を持つか
B = 5
for i in range(N_COLOR):
    for u in range(N_VER):
        for v in range(u+1, N_VER):
            J[u*N_COLOR+i, v*N_COLOR+i] = 2 * B
    
    for u, v in list(G.edges()):
        J[u*N_COLOR+i, v*N_COLOR+i] = -B

# QUBO行列を作成
Q = J
for i in range(N):
    if (i,i) not in Q.keys():
        Q[i,i] = h[i]
    Q[i,i] += h[i]
    
# 隣接行列を作成
for i in range(N):
    for j in range(N):
        if (i,j )in Q.keys() and Q[i,j] != 0:
            S[i,j] = 1

上で作成した隣接行列$S$を以下に示す。青は1、白は0を表している。

D-Wave 2000Qで解く

ランダムに生成したグラフを、その頂点をすべて含むようなクリークの集合に分割できるかを決定するクリーク頂点被覆問題を実装した。以下の場合でD-Wave 2000Qを用いて解いた。

例題1. 頂点数$10$のグラフ(ワッツ・ストロガッツモデル)を3個のクリークに分割する

例題2. 頂点数$16$のグラフ(いずれの頂点も次数が9)を4個のクリークに分割する

D-Wave SAPI Pythonスクリプトサンプル

D-WaveはC/C++、PythonのWeb APIを提供しており、先ほど記述したPythonコードからそのままD-Waveマシンに問題を投げることができる。まず、D-Waveマシンのグラフ上に今回の問題を埋め込む。適した埋め込みが見つかると埋め込み方の情報が返ってくるので、それをD-Waveマシンに送信し、D-Waveマシンが計算した実行結果を元の形に戻す。

# はじめに、D-WaveのAPI(SAPI)に接続する
# 注：接続部のコードには認証コードが含まれるため省略している。
#    2つのメソッドを実行するだけで簡単に接続・ソルバー指定が完了する。

# Q行列をイジングに変換
(h, J, ising_offset) = qubo_to_ising(Q)

# グラフ構造を取得
A = get_hardware_adjacency(solver)

# ハミルトニアン埋め込み
embeddings = find_embedding(S, A)
[h0, j0, jc, emb] = embed_problem(h, J, embeddings, A)
emb_j = j0.copy()
emb_j.update(jc)

# ソルバーへ送信 (numreadsで実行回数を指定する)
result = solve_ising(solver, h0, emb_j, auto_scale=True, num_reads=100)

# 結果の逆埋め込み
answer = unembed_answer(result['solutions'], emb, 'minimize_energy', h, J)

結果

例題1. 頂点数$10$のグラフ(ワッツ・ストロガッツモデル)を3個のクリークに分割する

分割の成功例を2つ以下に示す。

また、他にも分割の仕方がいくつか見つかった。

D-Waveマシンから返ってくる解の候補の中には、クリークの数が最小でない場合も含まれている。

例題2. 頂点数$16$のグラフ(いずれの頂点も次数が9)を4個のクリークに分割する

解の候補の中には、クリークでない部分グラフ、つまり辺で結ばれていない頂点対を含む部分グラフに分割される場合があった。

考察

分割の仕方が複数見つかったことや、クリーク数が最小でない解が見つかったこと、クリークでない部分グラフに分割した解が見つかったことは、量子アニーリングが組合せ最適化問題の近似解法であることが要因である。

まとめ

彩色問題の一つであるクリーク被覆問題をD-Waveマシンで解いた結果と、PythonとD-WaveのAPIを用いて組合せ最適化問題を解く流れを紹介した。D-Waveマシンによる解の候補の多くは載せなかったが、多くの分割パターンが得られたことは興味深かった。また現在、クリーク被覆問題に関する日本語の情報が少ないため、この記事を読んでくださった方に少しでも役立てば幸いである。

今後行いたいこと

qbsolvを用いて、より大きなグラフにおける問題を解く
D-Waveから得られた解の候補から、最小のクリーク分割数を求める実装を行う
他のネットワークで同様に問題を解く（今回の実装で用いたPythonのパッケージ「NetworkX」には、様々なネットワークを生成できる）

本記事の担当者

丸山尚貴

Post Views: 467