宮城県の市区町村を塗り分けろ - グラフ彩色問題をD-Waveマシンで解く

本記事ではKarpの21のNP完全問題の一つであるグラフ彩色問題 (Graph Coloring)とそのQUBO表現について解説し、具体的な応用例として宮城県における市区町村の塗り分けをとりあげ、D-Wave 2000Qでの実装例をPython SAPIならびにqbsolvを用いて解いた実行結果について紹介する。

グラフ彩色問題

グラフ彩色問題 (Graph Coloring Problem)とは、与えられたグラフに対して、頂点や辺などの要素がある制約を満たすように色を割り当てる場合に、必要かつ最小な色数 (彩色数：Coloring Number)を求める問題である。特に、隣り合う頂点同士が異なる色になるように彩色する場合を頂点彩色問題 (Vertex Coloring)、隣り合う辺同士が異なる色になるように彩色する場合を辺彩色問題(Edge Coloring)、頂点彩色と辺彩色のいずれも考慮する場合を全彩色問題 (Total Coloring)という。

彩色問題 (Coloring Problem)には様々な種類がある。Karpの21のNP完全問題の中には、グラフ彩色問題 (本記事)、クリーク被覆問題 (Clique Cover Problem)、スケジューリング問題 (Job Sequencing with Integer Lengths)がある。

この記事では、宮城県における市区町村を頂点、隣接する市区町村を辺で結んだグラフの頂点彩色問題に取り組む。宮城県には35の市町村があり、県庁所在地の仙台市は、5つの区に分かれる。それらを合わせた39の市区町村における彩色問題を考える。

グラフ彩色問題のQUBO表現による定式化

変数: $x_{i,k} \in \{0, 1\}$ (都道府県$i$が色$k \in \{1, 2, \cdots, K_\mathrm{max}\}$であれば$1$, そうでなければ$0$)
目的関数:

$$ H = A \sum_{v} \left( 1- \sum_{i=1}^n x_{v,i} \right)^2 + B \sum_{(u,v) \in E} \sum_{i=1}^n x_{u,i} x_{v,i} $$

上記のように定式化したQUBO表現された目的関数から行列Qの要素を計算するPythonスクリプトを以下に示す。

# 市区町村の数
N_CITIES = 39

# 色数
N_COLOR = 4

# イジング変数の数
N = N_CITIES * N_COLOR

# h(局所磁場), J(相互作用の係数), S(隣接行列)
J = {}
S = {}
h = [0] * N

# 一つの市区町村には、1色のみ割り当てる
param_A = 1
for v in range(N_CITIES):
    for i in range(N_COLOR):
        h[v*N_COLOR+i] = -param_A

        for j in range(i+1, N_COLOR):
            if (v*N_COLOR + i, v*N_COLOR+j) not in J.keys():
                J[v*N_COLOR + i, v*N_COLOR+j] = 2 * param_A
            else:
                J[v*N_COLOR + i, v*N_COLOR+j] += 2 * param_A

# 隣り合う市区町村には、それぞれ異なる色を割り当てる
param_B = 2.5
for u, ne in neighbors.items():
    for i in range(N_COLOR):
        for v in (x-1 for x in ne):
            if u < v:
                for i in range(N_COLOR):
                    if (u*N_COLOR+i, v*N_COLOR+i) not in J.keys():
                        J[u*N_COLOR+i, v*N_COLOR+i] = param_B
                    else:
                        J[u*N_COLOR+i, v*N_COLOR+i] += param_B

# QUBO行列を作成                  
Q = J.copy()
for i in range(N):
    if (i,i) not in Q.keys():
        Q[i,i] = h[i]
    Q[i,i] += h[i]

# 隣接行列を作成
S = {}
for i in range(N):
    for j in range(N):
        if (i,j )in Q.keys() and Q[i,j] != 0:
            S[i,j] = 1

実行結果

今回、(1)SAPI (D-WaveのソルバーAPI)と、(2) qbsolv（D-Waveが開発しているソルバー、詳細はこの記事を参照）を用いてこの問題を解いた。

(1) SAPIを用いた場合

この問題をD-Wave 2000Qに1000回解かせ、その中で最もエネルギーの低い解を以下に示した。しかし、隣り合う市区町村に同じ色が割り当てられたものが含まれていた。また、D-Waveが提供している埋め込みアルゴリズムを用いると、埋め込みに時間がかかった。

(2) qbsolvを用いた場合

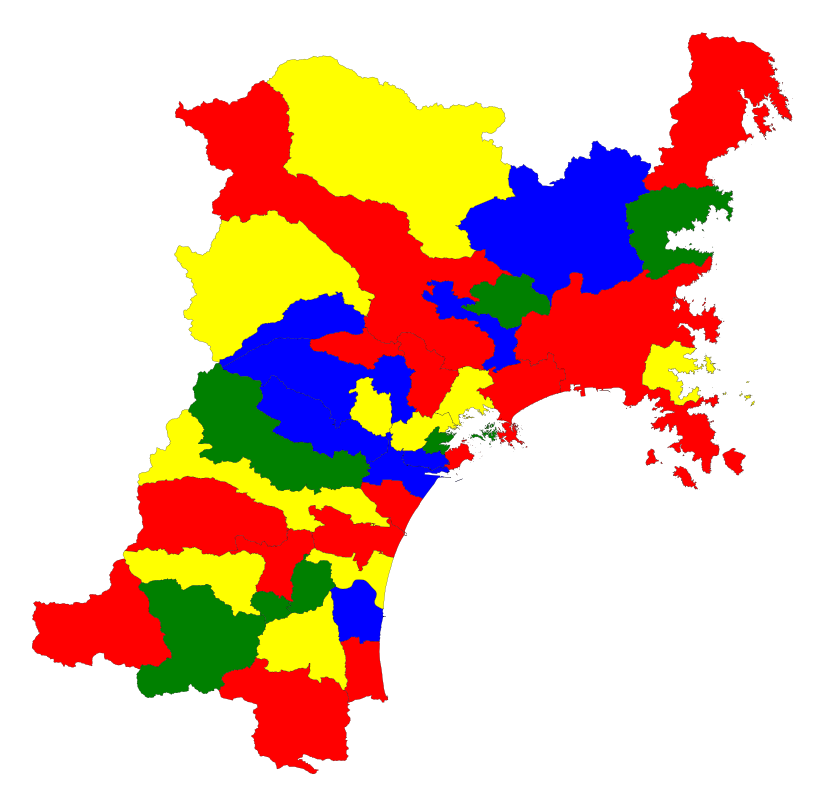
SAPIを用いて解を求める中で見つけたパラメータ(A, B)に設定し、qbsolvを用いて解いた結果を以下に示した。中央部の市区町村が密集した部分もきれいに彩色できていることが分かる。

まとめ

qbsolvを用いて、宮城県における市区町村をうまく塗り分けることができた。現在のD-Waveマシンでは解くことができる問題の大きさに限界があるが、今後のハードウェアの進歩に合わせて、より大きなグラフ彩色問題を解くことが期待できる。また、今回は頂点彩色問題を扱ったが、また機会があれば辺彩色問題やスケジューリング問題にも取り組んでいきたい。

参考

本記事の担当者

丸山尚貴

Post Views: 458

T-QARD Harbor

宮城県の市区町村を塗り分けろ – グラフ彩色問題をD-Waveマシンで解く