- タイトル: Traffic signal optimization on a square lattice with quantum annealing
- 著者: Inoue, D., Okada, A., Matsumori, T. et al.
- 書誌情報: Sci Rep 11, 3303 (2021)
- DOI: https://doi.org/10.1038/s41598-021-82740-0
背景
様々な交通信号制御
現在、多くの信号機には定周期制御という手法が使われています(fig1)。これは、青信号◯秒、赤信号△秒という設定をひたすら繰り返す手法です。具体的な秒数は、道路の大きさや過去の交通量などの情報から決定されます。
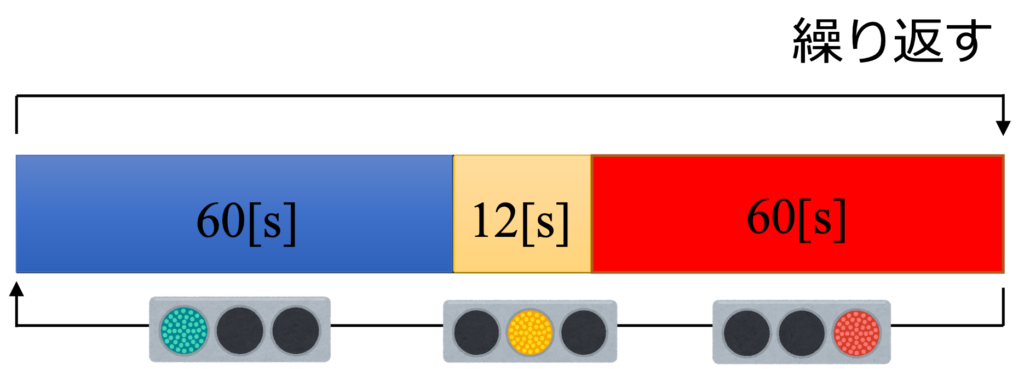
fig1. 定周期制御の例
定周期制御は最も簡単な制御方法ですが、渋滞が起きやすいという欠点があります。そこで、渋滞が起きやすい交差点をリアルタイムで制御する手法が生まれました。それが交通感応制御です。これは交通情報をリアルタイムで取得し、交通管制センターが自動or手動で信号機を制御します。交通感応制御は局所的に渋滞を解消できますが、周りの交差点にしわ寄せが来る可能性があります。
本論文の目的
交通感応制御のような局所的に最適な制御は、都市全体で最適な制御とは言いにくいです。しかし、全体制御の計算量は都市の大きさに比例して指数関数的に増大します($N$個の交差点がある場合、計算量は$2^N$となる)。そこで、本論文では高速かつ高精度な解探索が期待されている量子アニーリングマシンを用いて信号機の全体制御手法を提案します。
準備
量子アニーリングマシンとは
本論文の量子アニーリングマシンは、D-Wave 2000Qのことを指します。2000Qでは、最大2048個の量子ビットが使用可能です。また、アニーリングマシンを使用するには、最適化問題をイジングモデルに変換する必要があります。
$$イジングモデル: H=\sum_{i \neq j} J_{i j} \sigma_i \sigma_j+\sum_i h_i \sigma_i$$
相互作用$J_{ij}$と局所磁場$h_{i}$をマシンに入力することで、解候補$\boldsymbol{\sigma}$が出力されます。
問題設定
本論文では、単純化した都市を想定しています。
都市と信号の状態
$L \times L$の正方格子状を考えます(fig2 (a))。また、各交差点では2パターンの信号の状態を取ります(fig2 (b))。縦方向が青のときを、$\sigma = +1$、横方向が青のときを、$\sigma = -1$で表します。
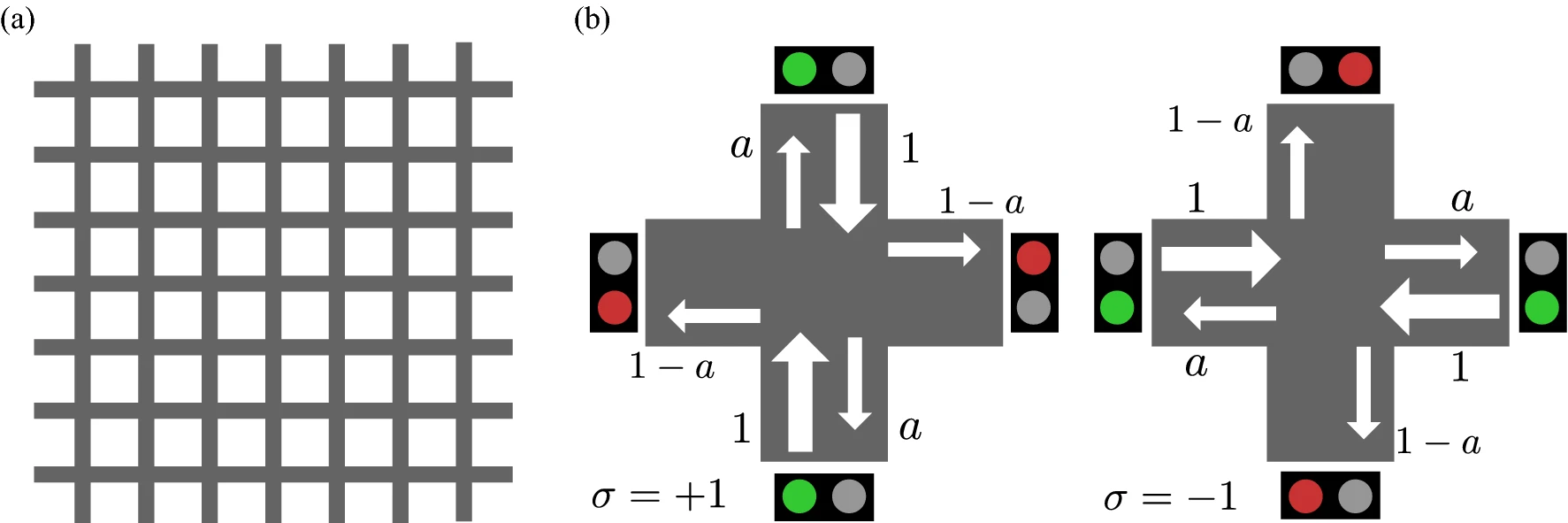
fig2. 都市と信号の状態, (https://doi.org/10.1038/s41598-021-82740-0)
自動車の動き方
自動車は交差点に到達すると、$a$の確率で直進し、$1-a$の確率で右折or左折をします(fig3)。全ての自動車がこのようにランダムな動き方をします。また、マップ外に出た自動車は反対の道路から入ってきます(周期境界条件)。

fig3. 自動車の動き方
定式化の準備
本論文の目的は、都市全体で最適な信号制御です。ここでいう「最適」というのは、「車の流れを良くするような」という意味になります。この目的を達成するためには、混みそうな方向を青信号にするという方法が考えられます。そこで、次の章では道路の込み具合を定式化していきましょう。
混み具合の定式化
まずは、$j \rightarrow i$が縦方向の場合の道路(以下、$road_{ij}$と表す)上にいる車の数を考えましょう(fig4)。
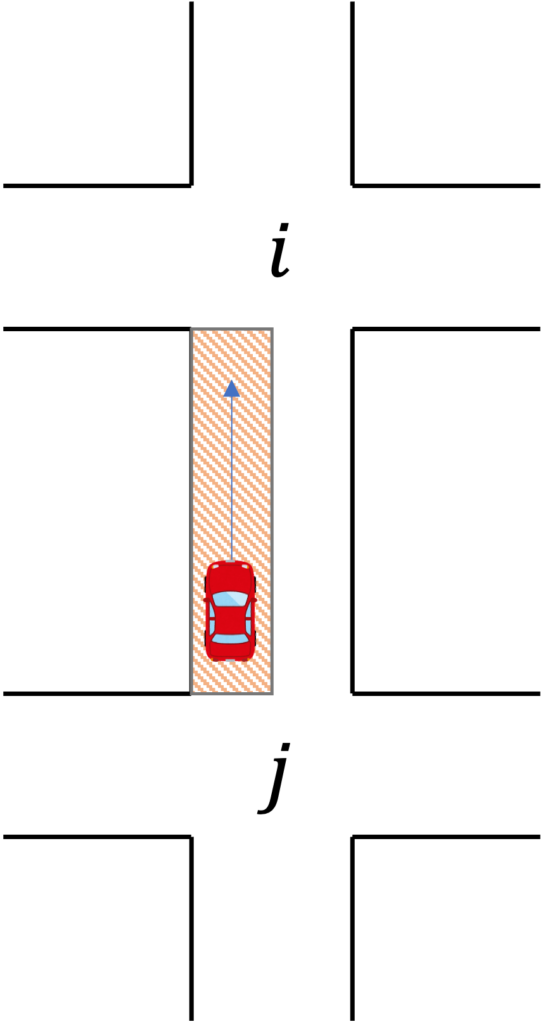
fig4. $j \rightarrow i$方向の道路上にいる車(赤車線部分)
ここで、$road_{ij}$を通過する単位時間当たりの平均台数$Q_{av}$[台/sec]が与えられているとします。これより、$\Delta t$[sec]間に通過する台数は$Q_{av} \Delta t$[台]となります。この内、何台が$road_{ij}$に残るのかは隣接する信号の状態から決まります(fig5)。そこで4パターンの信号の状態を考えていきましょう。
fig5.$road_{ij}$に残る台数の関係図
- $\sigma_i (t^∗)=+1, \sigma_j (t^∗ )=+1$のとき
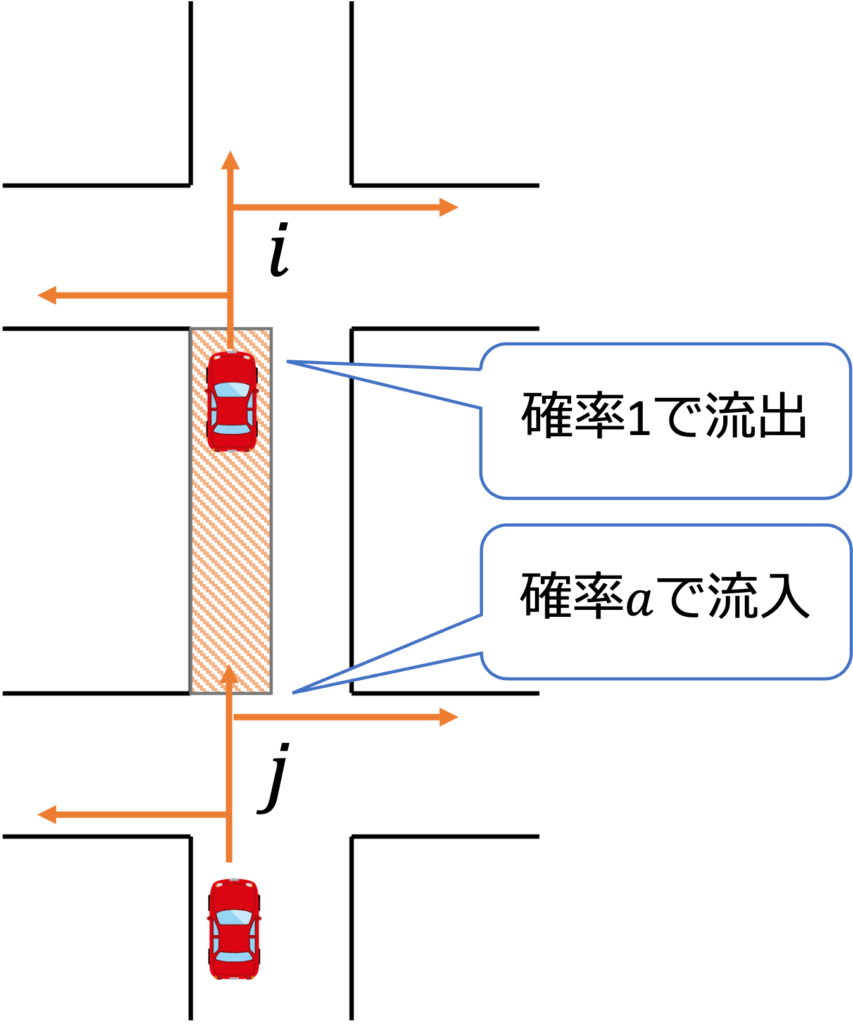
fig6. $\sigma_i (t^∗)=+1, \sigma_j (t^∗ )=+1$の場合
fig6より、$\Delta t$の間に$road_{ij}$から$(1-a)×Q_{av}\Delta t$[台]流出することが分かります。
- $\sigma_i (t^∗)=+1, \sigma_j (t^∗ )=-1$のとき
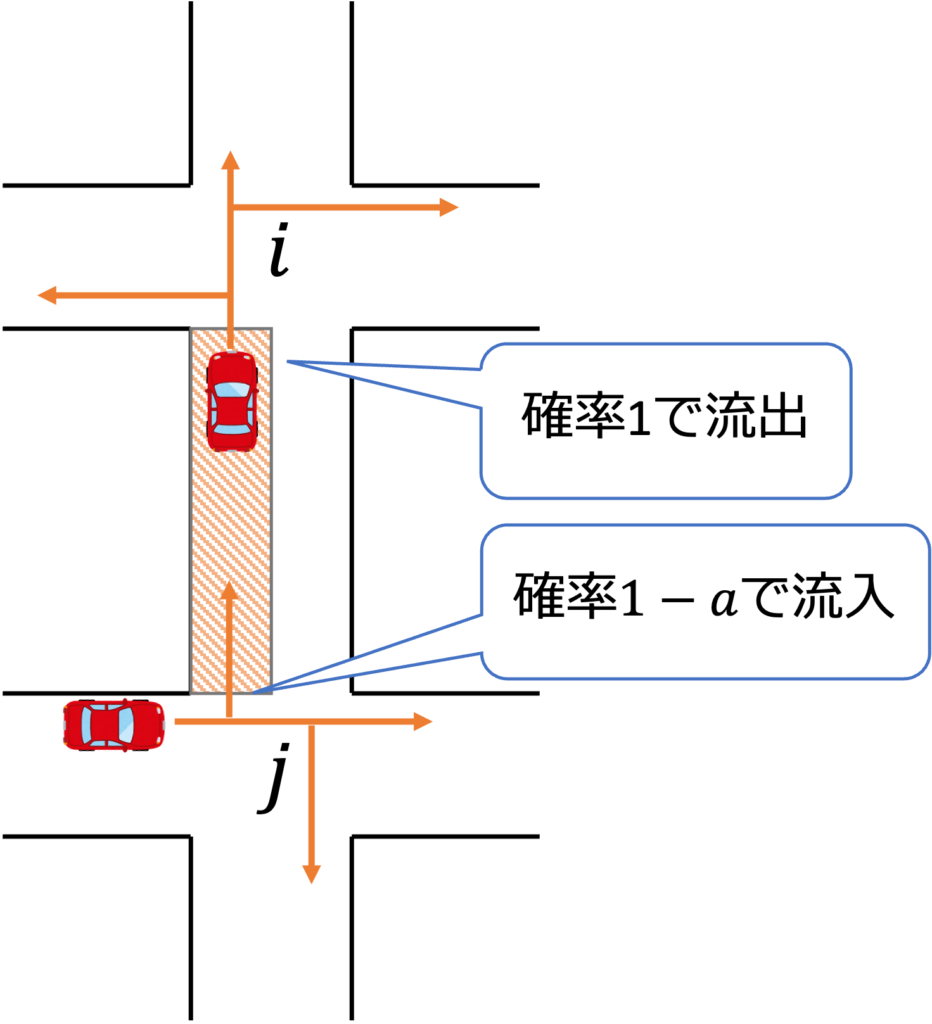
fig7. $\sigma_i (t^∗)=+1, \sigma_j (t^∗ )=-1$の場合
fig7より、$\Delta t$の間に$road_{ij}$から$a×Q_{av}\Delta t$[台]流出することが分かります。
- $\sigma_i (t^∗)=-1, \sigma_j (t^∗ )=+1$のとき
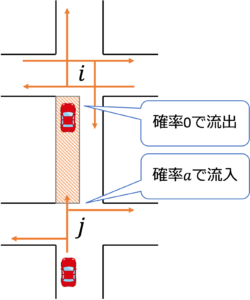
fig8. $\sigma_i (t^∗)=-1, \sigma_j (t^∗ )=+1$の場合
fig8より、$\Delta t$の間に$road_{ij}$に$a×Q_{av}\Delta t$[台]流入することが分かります。
- $\sigma_i (t^∗)=-1, \sigma_j (t^∗ )=-1$のとき
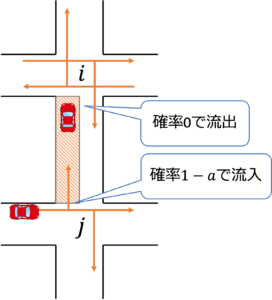
fig9. $\sigma_i (t^∗)=-1, \sigma_j (t^∗ )=-1$の場合
fig9より、$\Delta t$の間に$road_{ij}$に$(1-a)×Q_{av}\Delta t$[台]流入することが分かります。上記4パターンをまとめると次のようになります。ここで、流出する場合はマイナスで表すことで、「流入」する車の数としてまとめました。
| $\sigma_i$ | $\sigma_j$ | 流入する車の数 |
| +1 | +1 | $(a-1)×Q_{av}\Delta t$ |
| +1 | -1 | $-a×Q_{av}\Delta t$ |
| -1 | +1 | $a×Q_{av}\Delta t$ |
| -1 | -1 | $(1-a)×Q_{av}\Delta t$ |
これらを満たす式は、
$$(\Delta t \text{の間に流入する車の数})=\frac{1}{2} \lbrace -\sigma _i (t^∗)+(2a-1)\sigma _j (t^∗) \rbrace Q_{av} \Delta t$$
となります。$road_{ij}$が横方向のときも同様にして、
$$(\Delta t \text{の間に流入する車の数})=- \frac{1}{2} \lbrace -\sigma _i (t^∗)+(2\sigma -1)\sigma_j (t^∗) \rbrace Q_{av} \Delta t$$
となります。ここで、
$$s_{i j}=\left\{\begin{array}{cl}+1 & j \rightarrow i \text { が縦方向 } \\ -1 & j \rightarrow i \text { が横方向 }\end{array}\right\}$$
を用いると、上記2式は次のように表せます。
$$(\Delta tの間に流入する車の数)= \frac{s_{ij}}{2} \lbrace -\sigma _i (t^∗)+(2a-1)\sigma _j (t^∗) \rbrace Q_{av} \Delta t$$
これを用いて、車の数$q_{ij}^∗$に関する差分方程式が得られます。
$$q_{ij}^∗ (t^∗+\Delta t)=q_{ij}^∗ (t^∗ )+\frac{s_{ij}}{2} \lbrace -\sigma _i (t^∗ )+(2a-1)\sigma _j (t^∗ ) \rbrace Q_{av} \Delta t$$
両辺$Q_{av}\Delta t$で割ることにより、 $q_{ij}^∗$を正規化すると、
$$q_{ij}(t+1) = q_{ij}(t)+ \frac{s_{ij}}{2} \lbrace -\sigma _i (t)+α \sigma _j (t) \rbrace$$
となります。ここで、$ q_{ij}(t):=q_{ij}^{∗}(t^*)/(Q_{av}\Delta t), t:=t^{∗}/\Delta t, \alpha:=2a-1$です。$q_{ij}$ は正確には車の数ではないので、「混み具合」と呼ぶことにしましょう。この式を用いて、現在の時刻$t$の信号の状態から、次の時刻$t+1$における混み具合$q_{ij} (t+1)$が予想できます。これより、混みそうな方向を青信号にするような定式化を考えていきましょう。
混みそうな方向を青にする
ここで、縦方向と横方向の混み具合の差を考えましょう。
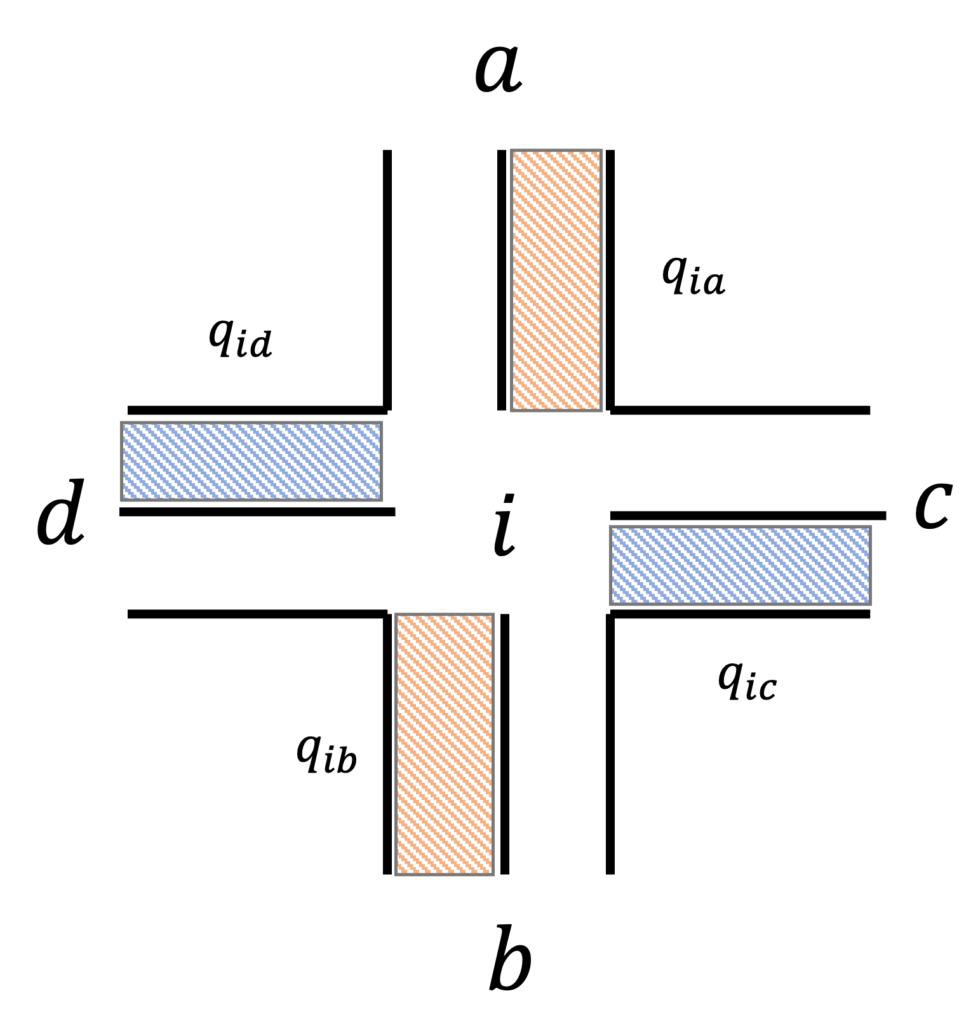
fig10. 交差点$i$に隣接する交差点$a, b, c, d$
fig10において、縦方向と横方向の混み具合の差は、
$$\frac{1}{2}\left(q_{i a}+q_{i b}\right) – \frac{1}{2}\left(q_{i c}+q_{i d}\right)$$
となります。これが正なら縦方向が、負なら横方向が混んでいると表せます。従って、時刻$t+1$における混み具合の差$x_{i}(t+1)$は、
$$x_{i}(t+1) = \frac{1}{2}\left(q_{i a}+q_{i b}\right) – \frac{1}{2}\left(q_{i c}+q_{i d}\right) = \frac{1}{2} \sum_{j \in N(i)} s_{ij}q_{ij}(t+1)$$
と表せます。ここで、$N(i)$は$i$に隣接する交差点の集合です。先程求めた混み具合$q_{ij}(t+1)$を代入すると、
$$
\begin{equation}
\begin{split}
x_{i}(t+1) &= \frac{1}{2} \sum_{j \in N(i)} s_{ij} \lbrace q_{ij}(t)+ \frac{s_{ij}}{2} \lbrace -\sigma_i (t)+α\sigma_j (t) \rbrace \rbrace \\
&= x_{i}(t)+ \lbrace -\sigma_{i}(t) + \frac{\alpha}{4} \sum_{j \in N(i)} \sigma_{j}(t) \rbrace
\end{split}
\end{equation}
$$
と変形できます。これより、混み具合の差$x_{i}$と信号機の色$\sigma_{i}$の関係式が導出できました。
ここまでのまとめ
混んでる方向を青信号にするために、混み具合の差を定式化しました。
$$
\begin{equation}
\begin{split}
x_{i}(t+1) &= \text{(縦方向の混み具合) – (横方向の混み具合)}\\
&= x_{i}(t)+ \lbrace -\sigma_{i}(t) + \frac{\alpha}{4} \sum_{j \in N(i)} \sigma_{j}(t) \rbrace
\end{split}
\end{equation}
$$
従って、
$$\left\{\begin{array}{cl}\sigma_{i}(t+1)\leftarrow +1 & \text{if } x_{i}(t+1)>0 \\ \sigma_{i}(t+1)\leftarrow -1 & \text{if } x_{i}(t+1)<0\end{array}\right\}$$
とすれば良さそうです。しかし、これでは局所制御になってしまい、全体制御をするという目的を果たせません。そこで、$x_{i}$をベクトル形式で表してみましょう。
目的関数
$$x_{i}(t+1) = x_{i}(t)+ \lbrace -\sigma_{i}(t) + \frac{\alpha}{4} \sum_{j \in N(i)} \sigma_{j}(t) \rbrace$$
をベクトル化すると次のようになります。
$$\mathbf{x}(t+1) = \mathbf{x}(t)+ \left( -\mathbf{I} + \frac{\alpha}{4} A \right)\boldsymbol{\sigma}(t)$$
ここで、$\mathbf{I}$は単位行列で、$A$は隣接行列です。混んでる方向を青信号にするということは、混み具合の差を0にするということに等しいです。つまり、$\mathbf{x}(t+1)$を0に近づけるような$\boldsymbol{\sigma}(t)$を選べば良いでしょう。従って、目的関数は、
$$\min \quad \mathbf{x}(t+1)^{T}\mathbf{x}(t+1)$$
となります。これを最小化するような$\boldsymbol{\sigma}$を選ぶことで、全体制御を実現することができます。しかし、これだけでは信号の色が頻繁に変わってしまう可能性があります。というのも、信号が頻繁に切り替わると、歩行者が渡りきれない等の問題が生じるからです。そこで、次の制約条件を加えます。
$$\min \quad \eta \left( \boldsymbol{\sigma}(t) – \boldsymbol{\sigma}(t-1) \right)^{T} \left( \boldsymbol{\sigma}(t) – \boldsymbol{\sigma}(t-1) \right)$$
$\eta$はハイパーパラメータです。この制約により、信号が切り替わるとペナルティが発生します。従って、最終的な目的関数は次のようになります。
$$H \left( \boldsymbol{\sigma}(t) \right) = \mathbf{x}(t+1)^{T}\mathbf{x}(t+1) + \eta \left( \boldsymbol{\sigma}(t) – \boldsymbol{\sigma}(t-1) \right)^{T} \left( \boldsymbol{\sigma}(t) – \boldsymbol{\sigma}(t-1) \right)$$
ここで、D-Waveマシンに入力できるように式変形を行いましょう。
$$
\begin{equation}
\begin{split}
H \left( \boldsymbol{\sigma}(t) \right) &= \mathbf{x}(t+1)^{T}\mathbf{x}(t+1) + \eta \left( \boldsymbol{\sigma}(t) – \boldsymbol{\sigma}(t-1) \right)^{T} \left( \boldsymbol{\sigma}(t) – \boldsymbol{\sigma}(t-1) \right)\\
&= \boldsymbol{\sigma}(t)^T(B^TB+\eta \mathbf{I})\boldsymbol{\sigma}(t) + (2\mathbf x (t)^TB – 2\eta \boldsymbol{\sigma}(t-1))\boldsymbol{\sigma}(t)+c(t)\\
&= \boldsymbol{\sigma}(t)^T J \boldsymbol{\sigma}(t)+ h \boldsymbol{\sigma}(t) + c(t)
\end{split}
\end{equation}
$$
ここで、$B := (-\mathbf{I}+\frac{\alpha}{4}A)、c(t)$は定数項です。相互作用$J$と局所磁場$h$を入力することで、解候補を得ることが出来ます。
実験
実験は、各ステップで信号の状態を決定します。その時に用いる手法は3種類あります。
手法の詳細
- 局所制御
各交差点の混み具合は、次のように表すことが出来ました。
$$x_{i}(t+1) := \text{(縦方向の混み具合) – (横方向の混み具合)}$$
従って、各交差点について次の操作を実行します。
$\left\{\begin{array}{cl}\sigma_{i}(t+1)\leftarrow +1 & \text{if } x_{i}(t+1)>0 \\ \sigma_{i}(t+1)\leftarrow -1 & \text{if } x_{i}(t+1)<0\end{array}\right\}$
この制御方法は、隣接する交差点の交通状況に関わらず、混んでる方向をただひたすら青信号にするという点で局所制御と言えます。
- シミュレーテッド・アニーリング(SA)
D-Waveのnealライブラリを使用します。
- 量子アニーリング(QA)
D-Wave 2000Q を使用します。ただし、D-Wave 2000Qは使用できる量子ビットに制限があるため、グラフ分割を行います。
グラフ分割
グラフが全結合の場合、2000Qの扱える最大変数は64変数です。従って、$L^2\leq64\Leftrightarrow L\leq8$を満たすように分割します。実際に分割した相互作用$J$を以下のfig11に示します。

fig11. 分割された相互作用, (https://doi.org/10.1038/s41598-021-82740-0)
分割にはMetisというグラフ分割ソフトウェアが使われています。
実験設定
| 定数 | 値 | |
| 直進確率 | $a$ | 0.9 |
| ハイパーパラメータ | $\eta$ | 1.0 |
| 混み具合の初期値 | $\mathbf{x}(0)$ | [-5.0,5.0]の範囲で一様分布に従う乱数 |
| 信号の状態の初期値 | $\boldsymbol{\sigma}(0)$ | {±1}の2項分布に従う乱数 |
実験の様子
上記の設定で1つ目の実験を行います。$t=100$時点での交差点の様子を見てみましょう。
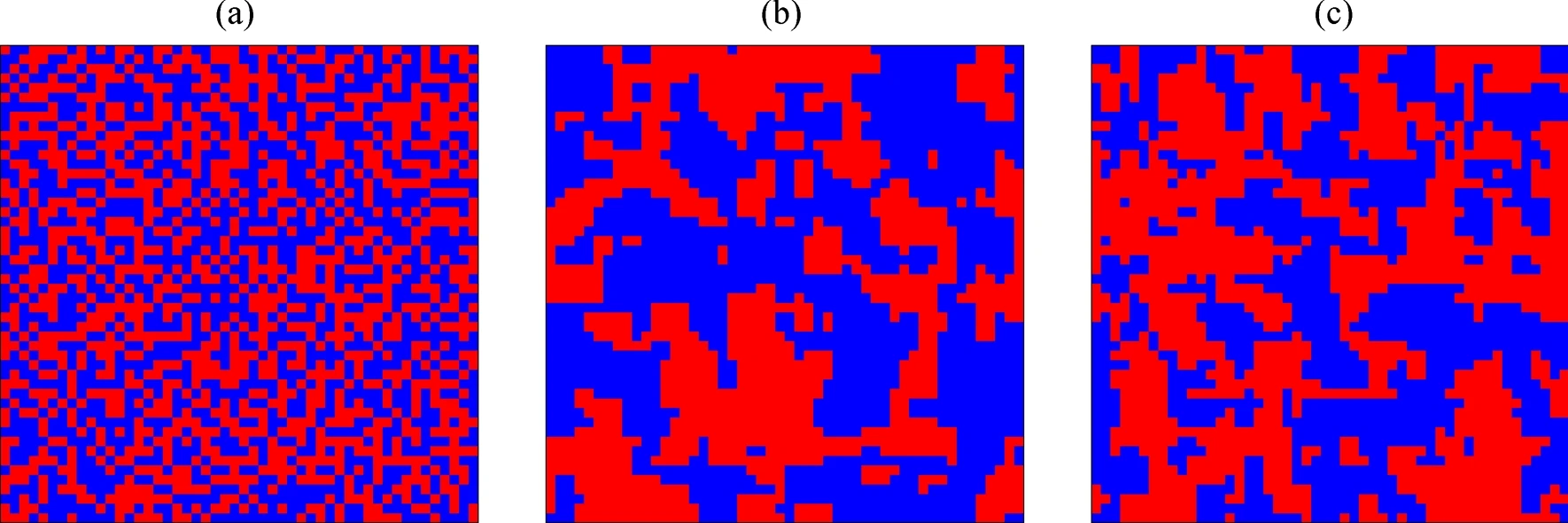
fig12. $t=100$時点での交差点。(a)が局所制御、(b)がSA、(c)がQAの場合, (https://doi.org/10.1038/s41598-021-82740-0)
赤は、$\sigma _{i} = +1$。青は、$\sigma _{i} = -1$を示しています。局所制御に比べて、SAやQAでは青色や赤色の大きなクラスターが出来ています(fig12)。クラスターが出来ていると次の交差点でもスムーズに進めるため、直感的にはSAやQAで最適化が上手く行っているように思えます。以降の実験では、本当にSAやQAが局所制御よりも優位なのか検証していきます。
ハミルトニアンの計測
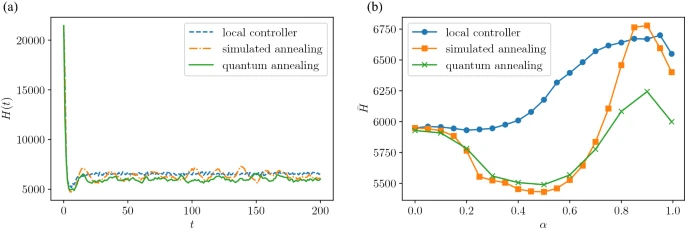
fig13.(a)横軸が時刻、縦時刻がハミルトニアン。(b)横軸が直進確率に関わるパラメータ、縦軸が平均ハミルトニアン, (https://doi.org/10.1038/s41598-021-82740-0)
fig13(a)を見て下さい。緑色がQAの結果です。ほとんどすべての時刻で、QAのハミルトニアンが最も低い値になっています。また、QAとSAが振動的になっていることも読み取れます。
考察(a)
まずは、QAとSAが振動的になったことについての考察です。本論文では、$t+1$時点で最適な解を出力するような目的関数を設計しました。しかし、その解が$t+2,t+3,…$で渋滞を引き起こす要因になっている可能性があります。そのため、ハミルトニアンは振動的になったと考えられます。
続いて、QAが最も優位になったことに対する考察です。D-Wave 2000Qは、相互作用$J$がスパースだと解の精度が向上することが知られています。今回使用した相互作用を展開すると、次のような形になります。
$$J = (1+\eta)\mathbf{I}-\frac{\alpha}{2}A+\frac{\alpha^{2}}{16}A^{T}A$$
ここで、 $A$は隣接行列なので、各列の非ゼロ要素は4個(fig14(a)、緑色ノード)です。また、$A^{T}A$の各列の非ゼロ要素は9個(fig14(a)、橙色ノード)です。従って、非ゼロ要素の総数は、$13L^2$となります。これより、$J$の疎密度は、
$$S_{J}(L)=(ゼロ要素数)/(全要素数)=(L^{4} – 13L^{2})/L^{4}$$
で表されます。
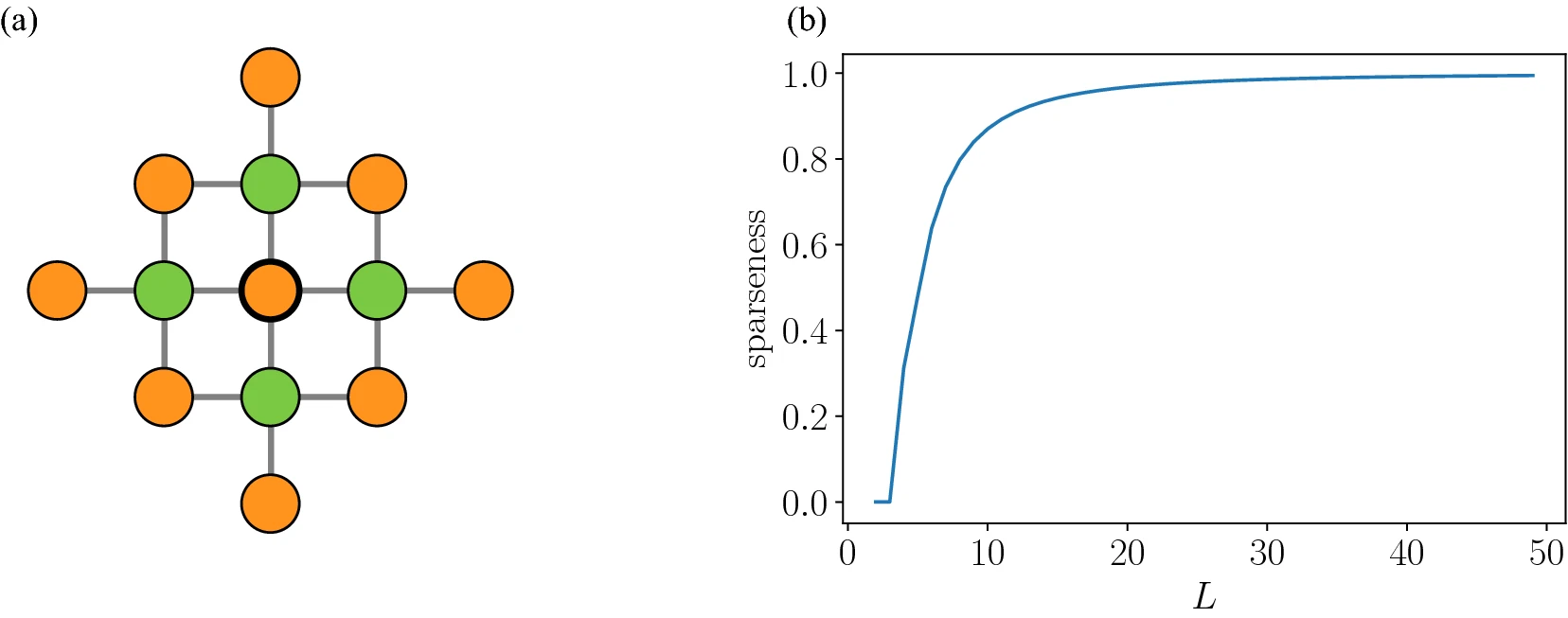
fig14.(a)グラフの隣接関係、(b)都市サイズと疎密度の関係, (https://doi.org/10.1038/s41598-021-82740-0)
これより、$L→∞$のとき、$S_J (L)→1$となります。つまり、都市サイズが大きくなると、スパース性が高くなるということです。これらの議論より、本論文の$L=50$の場合ではスパース性が高く(fig14(b)参照)、D-Wave 2000Qが優位になったと考えられます。
ハミルトニアンの時間発展
続いて、fig13(b)の結果を見ていきましょう。$\alpha$を変化させたときの時間平均ハミルトニアンをfig13(b)は示しています。これより、$\alpha$が0に近づくと、3手法とも同じ値に収束することが読み取れます。また、$\alpha=0.5$付近ではSAとQAに差はほとんどないものの、$\alpha=0.8$付近でSAのハミルトニアンが急激に上昇していることが分かります。
考察(b)
$\alpha\approx 0 \Leftrightarrow a = 1/2$のとき、相互作用と局所磁場は、
$$J\approx (1+\eta)I$$
$$h \approx -2 \left( \mathbf x(t)^T + \eta\boldsymbol{\sigma}(t-1)^T \right)$$
となります。$J$は対角行列なので$H(\boldsymbol{\sigma}(t))$の第1項は定数になります。従って、$ \boldsymbol{\sigma}$ は$h$の符号のみに依存して決定します。これを数式で表すと、
$$\sigma_i(t) = \left\{\begin{array}{cl} +1 & \text{if } x_i(t) + \eta\sigma_i(t-1)\geq 0 \\ -1 & \text{if } x_i(t) + \eta\sigma_i(t-1)<0\end{array}\right\}$$
となって、最適化制御と局所制御が等しくなり、3手法が同じ値に収束すると考えられます。
議論
QAは、グラフ分割をしてから問題を解く必要がありました。もし分割を行わずに解くことが出来れば、性能は向上するのでしょうか?そこで、SAを用いて「分割した場合」と「分割しない場合」で平均ハミルトニアンを計測しました。
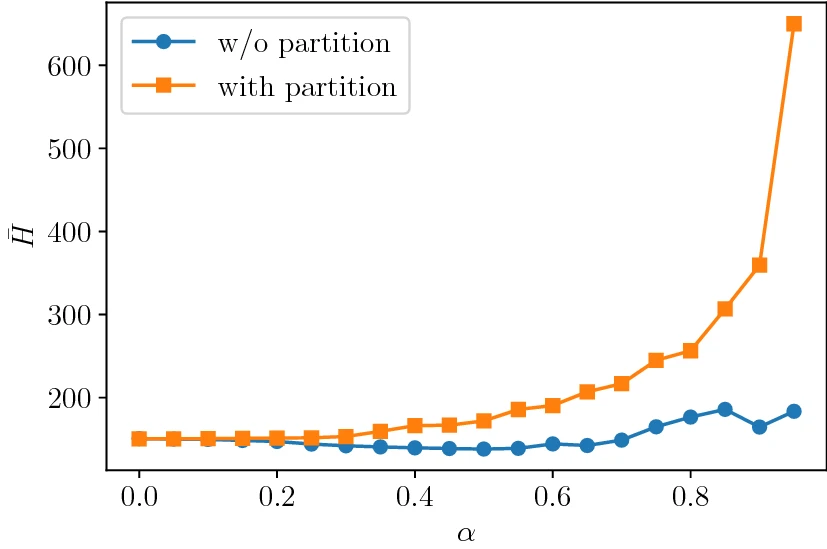
fig15. 直進確率を平均ハミルトニアンの関係(都市サイズは、$L=8$), (https://doi.org/10.1038/s41598-021-82740-0)
fig15において、「w/o partition」が分割しない場合、「with partition」が分割をした場合です。やはり$\alpha$が大きくなるにつれ、分割しない場合が優位になりました。これより、D-Waveマシンの扱える変数が増え、グラフ分割せずにQAで解くことができれば、さらなる性能向上が期待できるでしょう。
まとめ
- 車の直進確率$a$が$0.5$付近では、局所制御と最適化制御(SA, QA)に差は出ない。
- 車の直進確率が高いほど、QAで解くことが優位になる。
- グラフ分割せずにQAで解くことができれば、さらにQA が優位になるだろう。
あとがき
信号の色が青と赤の2パターンのみという単純な設定では、実際の交差点に適用するのは難しいと思いました。また、目的関数の最小化が本当に渋滞解消に繋がっているのか疑問でした。ハミルトニアンの比較だけでなく、車の停止時間等の測定結果も見たかったです。最後のグラフ分割の効果を検証する際に、なぜ$L=8$としたのか疑問が残りました。SAなら$L=50$で検証することも可能だったのではないかと思います。
本記事の担当者
鹿内怜央