文献情報
- タイトル : Solving Inequality-Constrained Binary Optimization Problems on Quantum Annealer
- 著者 : Kouki Yonaga、Masamichi Miyama、Masayuki Ohzeki
- 書誌情報 ( DOI ) : https://doi.org/10.48550/arXiv.2012.06119
概要
最適化問題の中には、不等式の形で表される制約 ( = 不等式制約 ) を含む問題が多くあります。この不等式制約を扱う際に、従来の手法ではスラック変数と呼ばれる補助変数が用いられています。しかし、スラック変数は二値変数を用いて表し直さなければならないため、多数の物理量子ビットが追加で必要となります。それにより、現行の量子アニーリングマシンを使って解くことのできる問題は小規模なものに限定されています。
そこで、本論文では、交互方向乗数法 ( ADMM ) という既存のアルゴリズムと量子アニーリングを組み合わせた新たなアルゴリズムを提案しています。このアルゴリズムにより、不等式制約をスラック変数なしで扱うことができ、従来よりも大規模な問題を解くことが可能となります。
本アルゴリズムの性能を検証するために、本論文では 2 次ナップサック問題 ( QKP ) を用います。そして、本アルゴリズムによって得られた QKP に対する解の精度を Gubori オプティマイザによって得られる厳密解と比較します。
課題
量子アニーリング ( QA : Quantum Annealing ) は、組合せ最適化問題を解くための技術です。そして、QA を実行するマシンを量子アニーリングマシンと呼びます。本論文では、D-Wave Systems が開発した量子アニーリングマシン ( = D-Wave マシン ) を使用します。現行の D-Wave マシンである D-Wave 2000Q は、以下の最小化問題を解きます。
$$ \underset{\bm{x}} {\rm{minimize}} \quad {\bm{x}}^{\top} Q {\bm{x}} \tag{1} $$
ここで、 $\bm{x} \in \{ 0,1 \}^{N}$ は $N$ 次元の二値ベクトル、 $Q$ は実数または整数の行列です。この問題を二次制約無し二値最適化問題 ( QUBO : Quadratic Unconstrained Binary Optimization ) と呼び、 $Q$ を QUBO 行列と言います[1]。
従って、D-Wave 2000Q を用いて問題を解くためには、対象の問題を QUBO 形式で表現する必要があります。今、対象の問題が以下の線形制約を含む最適化問題として与えられると仮定します。
$$ \begin{split} \underset{\bm{x}} {\rm{minimize}} \quad &f({\bm x}) \\ {\rm subject \ to} \quad &\bm{F}^{\top}_{l} \bm{x} = C_{l} \qquad(l=1,\cdots, L) \\ &\bm{G}^{\top}_{m} \bm{x} \leq D_{m} \quad (m=1,\cdots, M) \\ \end{split} \tag{2}$$
ここで、${\bm F}_{l}, \ {\bm G}_{m} \in \mathbb{Z}^{N}$ ( $\mathbb{Z}$ は整数の集合 )、$C_{l}, \ D_{m} \in \mathbb{Z}$ であり、$f(\bm{x})$ は QUBO 形式で与えられる目的関数です。$l$ は等式制約の番号を表す添え字、$m$ は不等式制約の番号を表す添え字です。
今、この問題を式 (1) の QUBO 形式に変換することを考えます。QUBO 形式は「制約無し」の最適化問題なので、等式制約 ${\bm F}^{\top}_{l} {\bm x} = C_{l}$ と不等式制約 ${\bm G}^{\top}_{m} {\bm x} \leq D_{m}$ を目的関数に含める形で表現し直さなければなりません。そのために用いられる方法の一つに「罰金法」と呼ばれるものがあります。
まずは、等式制約の方に罰金法を適用します。罰金法では、等式制約 ${\bm F}^{\top}_{l} {\bm x} = C_{l}$ $(l=1,\dots,L)$ を以下のように表現します。
$$ \displaystyle \sum_{l=1}^{L} ( \bm{F}^{\top}_{l} \bm{x} -C_l )^2 \tag{3}$$
そして、式 (3) を目的関数 $f({\bm x})$ に加えることにより、式 (2) は以下の問題に置き換わります。
$$ \begin{split} \underset{\bm{x}} {\rm{minimize}} \quad &f({\bm x}) + \alpha \sum_{l=1}^{L}(\bm{F}^{\top}_l \bm{x} – C_l)^2 \\ {\rm subject \ to} \quad &\bm{G}^{\top}_{m} \bm{x} \leq C_{m} \qquad(m=1,\cdots, M) \\ \end{split} \tag{2′} $$
式 (2) には ${\bm F}^{\top}_{l} {\bm x} = C_{l}$ $(l=1,\dots,L)$ という制約がありましたが、式 (2’) ではそれが無くなり、代わりに目的関数に式(3)の項を $\alpha$ 倍したものが足されています。これにより、制約を満たさなかった場合 ( すなわち ${\bm F}^{\top}_l {\bm x} – C_l \ne 0$ の場合 )、その誤差の二乗を $\alpha$ 倍したものがコスト関数に足されることになります。係数 $\alpha$ は罰金係数と呼ばれ、式 (3) の項がコスト関数に及ぼす影響の強さを決めるパラメータです。そのため、$\alpha$ は $ f ( {\bm x} ) $ よりも相対的に大きな値に設定します。
以上のようにして制約を目的関数に含める手法を罰金法と言います。また、罰金法により目的関数に加わる項を「罰金項」と呼び、制約を目的関数に含めることを「緩和」と呼びます。同じようにして、不等式制約 ${\bm G}^{\top}_{m} {\bm x} \leq D_{m}$ についても以下のように表現することができます。
$$ \displaystyle \sum_{m=1}^{M} ({\bm G}^{\top}_{m} {\bm x}-D_{m}+s_{m})^2 \tag{4} $$
ただし、$s_m \in \{ 0,1,\cdots, D_m \}$ とします。この新たに追加された変数 $s_m$ のことを「スラック変数」と呼びます。このスラック変数 $s_m$ は変数 $\bm{x}$ と同様、QA によって最適解を求める対象になります。
式 (4) を目的関数に加えることにより、式 (2′) は以下の問題に緩和されます。
$$ \displaystyle \underset{\bm{x}} {\rm{minimize}} \quad f({\bm x}) + \alpha \sum_{l=1}^{L}({\bm F}^{\top}_{l} {\bm x} – C_l)^2 + \beta \sum_{m=1}^{M} ({\bm G}^{\top}_{m} \bm{x} -D_m + s_m)^2 \tag{2”}$$
これにより、式 (2) は制約無しの最適化問題になりました。ここで、$\beta$ は $\alpha$ と同様の罰金係数です。しかし、$s_m \in \{ 0,1,\cdots, D_m \}$ であるため、 $D_m \geq 2$ のとき $s_m$ は二値変数ではありません。QUBO は「二値」最適化問題なので、$s_m$ が二値変数でなかった場合、 $s_m = 2^{0} \times y_1 + 2^1 \times y_2 + 2^2 + y_3 + \cdots $ というように補助的な二値変数で表現し直す必要があります ( 詳しくは 9.2. 補足2 : スラック変数の二値変数による展開 にて簡単な例を用いて説明しています )。さらに、このような展開を全ての不等式制約 ${\bm G}^{\top}_m {\bm x} \leq D_m \ (m=0,1,2,\cdots,M)$ に対して行う必要があります。この展開により多くの二値変数が追加され、物理量子ビットが $y_1, y_2, y_3,\cdots$ の個数分だけ余計に必要となります。D-Wave 2000Q の物理量子ビット数は 2048 個であるため、スラック変数を使ってしまうと、変数 ${\bm x}$ の数が少ない ( = サイズの小さい ) 問題しか解けなくなってしまいます。
以上の理由から、不等式制約に対してスラック変数を用いることは得策ではありません。したがって、本論文ではスラック変数を使わずに解く方法を開発しています。そして、従来よりもサイズの大きな不等式制約付きの問題が解けることを示しています。
背景
最適化モードとサンプリングモード
本論文で使用する D-Wave 2000Q には「最適化モード」と「サンプリングモード」と呼ばれる 2 つの後処理のモードが搭載されています。6. 実験 では両モードの比較も行うため、ここではその 2 つのモードについて紹介します。
まず、最適化モードでは、QA で得られたサンプル ( 解の候補 ) に対して局所的な更新を行うことによって、より低いコスト関数を得ます。ここで、コスト関数とは、式 (2’’) のような、最適化問題を解くために最小化する関数のことです。すなわち、最適化モードは、解きたい最適化問題に対して、なるべく良い解を求めるためのモードです。
一方、サンプリングモードでは、QA によって得られたサンプルを、次のように定義される確率分布に修正します。
$$ P({\bm x}) = \frac{1}{Z} \exp [-\beta E({\bm x})] \tag{5}$$
式 (5) の確率分布はボルツマン分布と呼ばれます。ここで、$\beta$ は逆温度です。$\beta$ を変化させることにより、確率分布 $P({\bm x})$ が変化します。例えば、$\beta \to \infty $ とすると、エネルギー $E({\bm x})$ を最も小さくするサンプルのみが得られます。一方、$\beta \to 0$ とすると、$P({\bm x})$ から多様なサンプルが生成されることになります。このように、サンプリングモードはボルツマン分布からサンプルを取得したい場合に用いるモードです[2]。
方法
拡張ラグランジュ法
本論文で提案するアルゴリズムは、拡張ラグランジュ法と ADMM に基づいています。ここからは、スラック変数を使わずに不等式制約を緩和する方法を議論しながら、拡張ラグランジュ法と ADMM について説明していきます。
今回は、簡単のため式 (2) において不等式制約のみを考えます。不等式制約 ${\bm G}^{\top}_m {\bm x} \leq D_m \ (m=0,1,2,\cdots,M)$ を緩和するために、ここではヘヴィサイドの階段関数 $\Theta (x)$ を用います。
$$ \begin{equation} \Theta (x) = \left \{\begin{array}{l}1 {\rm if} \ x > 0 \\0 {\rm if}\ x \leq 0 \end{array}\right.\end{equation} $$
$\Theta (x)$ のグラフを以下の図 1 に示します。
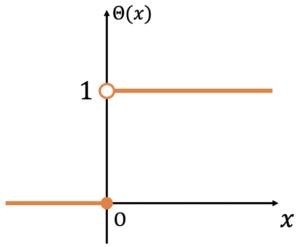
図1. ヘヴィサイドの階段関数 $\Theta({\bm x})$ のグラフ。
この階段関数 $\Theta (x)$ と罰金法を組み合わせることにより、不等式制約 ${\bm G}^{\top}_m {\bm x} \leq D_m \ (m=0,1,2,\cdots,M)$ を以下のように緩和することができます。
$$ E_{{\rm ineq}} ({\bm x}) = f({\bm x})+ \gamma \sum_{m=1}^{M} \Theta ({\bm G}^{\top}_{m} {\bm x} – D_m) \tag{6} $$
任意の $m$ について $\Theta ({\bm G}^{\top}_{m} {\bm x}^{\ast} -D_m)$ がゼロのとき、 ${\bm x}^{\ast}$ は実行可能解となります。それは、${\bm G}^{\top}_m {\bm x}^{\ast} \leq D_m \Leftrightarrow {\bm G}^{\top}_m {\bm x}^{\ast} – D_m \leq 0$ のとき、階段関数の定義より $\Theta ({\bm G}^{\top}_{m} {\bm x}^{\ast} – D_m)=0$ となるからです。これにより、スラック変数を使わなくても不等式制約を緩和することができました。
しかし、式 (6) は階段関数の中に変数 ${\bm x}$ が含まれているため、QUBO 形式にすることができません。したがって、このままでは D-Wave 2000Q を用いた最小化は不可能です。そこで、式 (6) のコスト関数を次の最適化問題に書き換えます。
$$ \begin{split} \underset{\bm{x}} {\rm{minimize}} \quad &f({\bm x}) + \gamma \sum_{m=1}^{M} \Theta(z_m) \\ {\rm subject \ to} \quad &\bm{G}^{\top}_{m} \bm{x} -D_m = z_m \qquad(m=1,\cdots, M) \\ \end{split} \tag{7} $$
ここで、 $\{ z_m \} \in \mathbb{Z}^N$ は補助変数です。すなわち、 $\Theta({\bm G}^{\top}_m {\bm x})$ が $\Theta(z_m)$ と等価になるように、制約として ${\bm G}^{\top}_m {\bm x} – D_m = z_m$ を課しています。これにより、階段関数の中には変数 ${\bm x}$ が無くなりました。ただし、新たな等式制約が登場したため、緩和し直す必要があります。このときに用いるのが「拡張ラグランジュ法」です。拡張ラグランジュ法を用いて等式制約を緩和したコスト関数 $E_{\rm{aug}}$ を以下のように定義します。
$$ \displaystyle E_{\rm aug}({\bm x},{\bm z},{\bm \lambda}) = f({\bm x}) + \gamma \sum_{m=1}^{M} \Theta(z_m)+ \sum_{m=1}^{M} \lambda_{m} ({\bm G}^{\top}_m {\bm x} – D_m – z_m) + \frac{\rho}{2} \sum_{m=1}^{M} ({\bm G}^{\top}_m {\bm x} -D_m -z_m)^2 \tag{8}$$
式 (8) の第 4 項は、式 (3) と同じ罰金項です。そして、第3項は「ラグランジュ未定乗数法」による項です。ラグランジュ未定乗数法は、罰金法と同じように制約を緩和する方法の一つです。罰金法との違いは、 $({\bm G}^{\top}_m {\bm x} – D_m – z_m)$ が 1 次になっている点と、係数 $\lambda_m$ が $m=1,2,\cdots, M$ という制約に依存している点です ( この係数はラグランジュ未定定数と呼ばれます )。
このように、拡張ラグランジュ法は、ラグランジュ未定乗数法と罰金法を組み合わせて制約を緩和する方法です。以降では、式 (8) を最小化することにより、対象の最適化問題を解くことを目指していきます。
ADMM
ADMMは、式 (8) のような、拡張ラグランジュ法を用いて定義したコスト関数を最小化するために広く用いられるアルゴリズムです。ADMM では、以下の 3 ステップからなる逐次最適化を繰り返し適用して ${\bm x}$、${\bm z}$、および乗数 ${\bm \lambda}$ を更新します。
$$ {\bm x}^{\ast}[t+1]=\underset{\bm{x}} {\rm{argmin}} \ \ E_{\rm aug}({\bm x}, {\bm z}^{\ast}[t+1], {\bm \lambda}[t]) \tag{9a}$$
$$ {\bm z}^{\ast}[t+1]=\underset{\bm{z}} {\rm{argmin}} \ \ E_{\rm aug}({\bm x}^{\ast}[t+1], {\bm z}, {\bm \lambda}[t]) \tag{9b}$$
$$ \lambda_{m}[t+1]=\lambda_{m}[t]+\rho ({\bm G}^{\top}_{m} {\bm x}^{\ast}[t+1] – D_m – z_m^{\ast}[t+1] ) \quad (m=1,\cdots,M) \tag{9c}$$
ここで、 $t$ は反復回数に相当します。収束するまで式 (9a) ~ (9c) を繰り返すことで、$E_{\rm aug}({\bm x},{\bm z},{\bm \lambda})$ を最小にする解を得ます。
すなわち、ADMM では、はじめに ${\bm z}$ を固定して ${\bm x}$ について最適化し ( 式 (9a) )、次に ${\bm x}$ を固定して ${\bm z}$ について最適化し ( 式 (9b) )、最後に最適化した ${\bm x}$ と ${\bm z}$ を用いて $\lambda_{m}$ を更新する ( 式 (9c) )、という 3 ステップを繰り返します。ポイントは、${\bm x}$ と ${\bm z}$ についての最適化を別々に行う点です。式 (9a) の ${\bm x}$ についての最適化では、 $E_{\rm aug}$ 内の階段関数に関する項は関係しないため QUBO 形式にすることができます。そのため、本論文では式 (9a) の ${\bm x}$ についての最適化に D-Wave 2000Q を用いています。
新しいアルゴリズム
本論文では、ADMM と QA を組み合わせたアルゴリズムを提案しています。通常の ADMM との主な違いは、上述の通り、式 (9a) を解くために D-Wave 2000Q を用いる点です。
本アルゴリズムでは、$E_{\rm aug}({\bm x},{\bm z},{\bm \lambda})$ に対して QA を適用して多数のサンプル $\{ {\bm x}_{\nu} \}$ ( $\nu$ は各サンプルのインデックス ) を取得します。そして、$E_{\rm aug}({\bm x},{\bm z},{\bm \lambda})$ を最小化する解 ${\bm x}^{\ast}_{\rm cost}$ を以下のように定義します。
$$ {\bm x}^{\ast}_{\rm cost}= \underset{ \{ {\bm x}_{\nu} \} } {\rm{argmin}} \ \ E_{\rm aug}({\bm x} = {\bm x}_{\nu},{\bm z},{\bm \lambda}) \tag{10}$$
すなわち、サンプル $\{ {\bm x}_{\nu} \}$ の中で $E_{\rm aug}$ を最小にするものを ${\bm x}^{\ast}_{\rm cost}$ とおきます。ここで、${\bm x}^{\ast}_{\rm cost}$ は必ずしも実行可能解である必要はありません。ただし、$\{ {\bm x}_{\nu} \}$ の他のサンプルは実行可能解とします。また、以下のように実行可能解 ( 不等式制約を全て満たす解 ) の中で $f({\bm x})$ を最小化する解 ${\bm x}^{\ast}_{\rm feas}$ を定義します。
$$ {\bm x}^{\ast}_{\rm feas} = \underset{ \{ {\bm x}_{\nu} \} } {\rm{argmin}}\ \ f({\bm x}) \ \ {\rm s.t.} \ \ {\bm G}^{\top}_{m} {\bm x} \leq D_m \quad(m=1,\cdots, M) \tag{11}$$
${\bm x}^{\ast}_{\rm cost}$ と ${\bm x}^{\ast}_{\rm feas}$ を別に定義したのは、${\bm z}$ と ${\bm \lambda}$ の更新には ${\bm x}^{\ast}_{\rm cost}$ を使用し、実行可能解の探索には ${\bm x}^{\ast}_{\rm feas}$ を使用するためです。
以下に、アルゴリズムの詳細を記載します。なお、本論文では QUBO を解くのに D-Wave 2000Q を用いていますが、他の QUBO ソルバを適用することも可能です。したがって、D-Wave 2000Q より多くの変数を扱うことができる QUBO ソルバを用いれば、さらにサイズの大きな不等式制約付きの最適化問題を解くことができます。
[ アルゴリズムの手順 ]
-
各パラメータを $\{ z_m \}=0$, $\{ \lambda_m \}=0$, $t=1$ と初期化する。
-
サイズ $N$ の完全グラフを embedding する。※ $N$ は変数 ${\bm x}$ の要素数 ( ${\bm x} \in \{ 0, 1 \}^N$ )。
- 式 (8) を用いて QUBO 行列を計算する。
- 計算した QUBO 行列を D-Wave 2000Q に適用し、サンプル $\{ {\bm x}_{\nu} \}$ を取得する。
-
サンプル $\{ {\bm x}_{\nu} \}$ を用いて、式 (10) と式 (11) から ${\bm x}^{\ast}_{\rm cost}$ と ${\bm x}^{\ast}_{\rm feas}$ を計算する。
-
$z_{m}^{\ast} = \min \ (0, {\bm G}^{\top}_m {\bm x}^{\ast}_{\rm cost} -D_m) \quad (m=1,\cdots,M)$ として ${\bm z}^{\ast}$ を更新する。
-
$\lambda_m = \lambda_m + \rho ({\bm G}^{\top}_m {\bm x}^{\ast}_{\rm cost} -D_m-z_m^{\ast}) \quad (m=1,\cdots,M)$ として ${\bm \lambda}$ を更新する。
-
収束しているかどうかを確認する ( 以下の基準のいずれかを満たした時に計算を終了する ) 。
-
$t>t_{\rm max}$
- $E_{\rm ineq}({\bm x}_{\rm feas}^{\ast})$ が $t_{\rm conv}$ 回のステップで改善されない
- $\sqrt{\sum_{m}({\bm G}^{\top}_m {\bm x}_{\rm feas} -D_m-z_m)^2} < \epsilon \qquad$ ※ $ t_{\rm max}, t_{\rm conv}, \epsilon$ は予め設定しておくパラメータ。
-
- $t \leftarrow t+1$
- 手順 3. ~ 9. を収束するまで繰り返す。
アルゴリズムにおいて、手順 3. ~ 5. が式 (9a) の ${\bm x}$ についての最適化、手順 6. が式 (9b) の ${\bm z}$ についての最適化、手順 7. が式 (9c) の ${\bm \lambda}$ の更新にあたります。手順 3. ~ 9. の反復において毎回 embedding することを避けるため、手順 2. では予め問題サイズ $N$ の完全グラフ ( すなわち全結合グラフ ) を embedding しています。一方で、unembedding は手順 4. で反復ごとに行われます ( embedding と unembedding に関しては 9.1.1. 補足1 : embeddingとunembedding で説明しています )。
実験
実験方法
QKP
本論文では、以下のように定義される 2 次ナップサック問題 ( QKP : Quadratic Knapsack Problem ) を用いて、本アルゴリズムの性能を検証します。ナップサック問題では、重量と価値を持つ荷物を、容量制限のある一つのナップサックに入れることを考えます。そして、ナップサックに入れた荷物の価値が最大になるような荷物の入れ方を求めます。すなわち、ナップサックの容量制限を不等式制約として含む最大化問題です。
$$ \begin{split} \underset{\bm{x}} {\rm{maximize}} \quad &{\bm x}^{\top} P {\bm x} \\ {\rm subject \ to} \quad &{\bm w}^{\top} {\bm x} \leq c\\ \end{split} \tag{7} $$
ここで、$P=\{ p_{i, j} \} \in \mathbb{Z}_{+}^{N \times N}$ ( $\mathbb{Z}_{+}$ は正の整数の集合) は荷物の価値を表す行列、 ${\bm w} = \{ w_i \} \in \mathbb{Z}_{+}^{N}$ は荷物の重量を表すベクトル、 $c \in \mathbb{Z}$ はナップサックの容量を表すスカラーです。変数 ${\bm x}=\{ x_i\} \ (i=1,\cdots, N)$ は以下のように定義されます。
$$ \begin{equation} \left \{\begin{array}{l}x_i = 0 {\rm if} \quad i \ 番目の荷物をナップサックに入れない \\x_i = 1 {\rm if}\quad i \ 番目の荷物をナップサックに入れる \end{array}\right.\end{equation} $$
行列 $P$ の非対角要素 $p_{i, j} \ (i \ne j)$ は、荷物 $i$ と荷物 $j$ が両方ナップサックに入れられた場合にのみ課される報酬です ( $x_i$ または $x_j$ がゼロのとき $x_i P_{i,j} x_j =0$ となるため)。なお、D-Wave 2000Q では最小化問題を扱うので、QUBO 形式にする際には、目的関数の符号を反転させて $f({\bm x}) = – {\bm x}^{\top} P {\bm x}$ とします。また、不等式制約については 5. 方法 で述べた手法で緩和します。
本実験では、 $P$ と ${\bm w}$ をランダムに生成します。具体的には、ペア $(i, j)$ の価値 $p_{i, j}$ を確率 $(1-\Delta)$ で 0 とし、確率 $\Delta$ で 1 ~ 100 の一様分布から選びます。つまり、 $\Delta$ が 1 に近いとき、QUBO 行列は非ゼロ要素が多くなり、$\Delta$ が 0 に近いとき、QUBO 行列は非ゼロ要素が少なくなります。したがって、変数同士の相互作用をグラフで表すと、$\Delta \approx 1$ のときそのグラフは密となり、$\Delta \approx 0$ のとき疎となります。また、重み $\{w_i\}$ は $[1, 50]$ からランダムに選び、容量 $c$ は $[50, \sum_i w_i]$ の一様分布から選びます。
MAPE
新しいアルゴリズムの典型的な性能を検証するために、10 個のインスタンスを生成します。インスタンスとは、上述の方法でランダムに生成した一つひとつの QKP のことです。そして、アルゴリズムの精度を検証するために、以下の平均絶対誤差 ( MAPE : Mean Absolute Percentage error ) を定義します。
$$ {\rm MAPE} = \frac{1}{N_{\rm inst}} \sum_{k=1}^{N_{\rm inst}} \frac{ |f_k ({\bm x}_{\rm opt}^{\ast}) – f_k ({\bm x}_{\rm feas}^{\ast})| }{f_k ({\bm x}_{\rm opt}^{\ast})} \tag{12}$$
ここで、$f_k({\bm x})$ は $k$ 番目のインスタンスの目的関数であり、$N_{\rm inst}$ はインスタンスの数 ( すなわち、ここでは $N_{\rm inst}=10$ ) です。また、${\bm x}_{\rm opt}^{\ast}$ は Gurobi オプティマイザ ( 最適化問題を厳密に解くソルバ ) で得られた最適解、${\bm x}_{\rm feas}^{\ast}$ は本アルゴリズムで得られた実行可能解です。${\rm MAPE} = 0$ のとき、全てのインスタンスで最適解が得られたことになります。
また、D-Wave 2000Q のアニーリング時間は $20 \ {\rm \mu s}$ に設定し、サンプルは 2000 個生成します。そして、アルゴリズムの予め決めておくパラメータは以下のように設定します。
$$ \rho = 0.1 \tag{13a} $$
$$ t_{\rm max}= 30 \tag{13b} $$
$$ t_{\rm conv} = 10 \tag{13c} $$
$$ \epsilon = 10^{-3} \tag{13d} $$
実験結果
QKP に対する解の精度の検証
QKP に対して ADMM アルゴリズムで得られた解の精度を MAPE によって評価した実験の結果を示していきます。以下の図 2 に、$\Delta=0.2, 0.6, 1.0$ のときの MAPE の $N$ – 依存性を示します。DW(opt) は 4. 背景 最適化モードとサンプリングモード で紹介した D-Wave 2000Q の最適化モードを使用した場合で、DW(β = …) は逆温度 $\beta$ が … のときのサンプリングモードを使用した場合です。
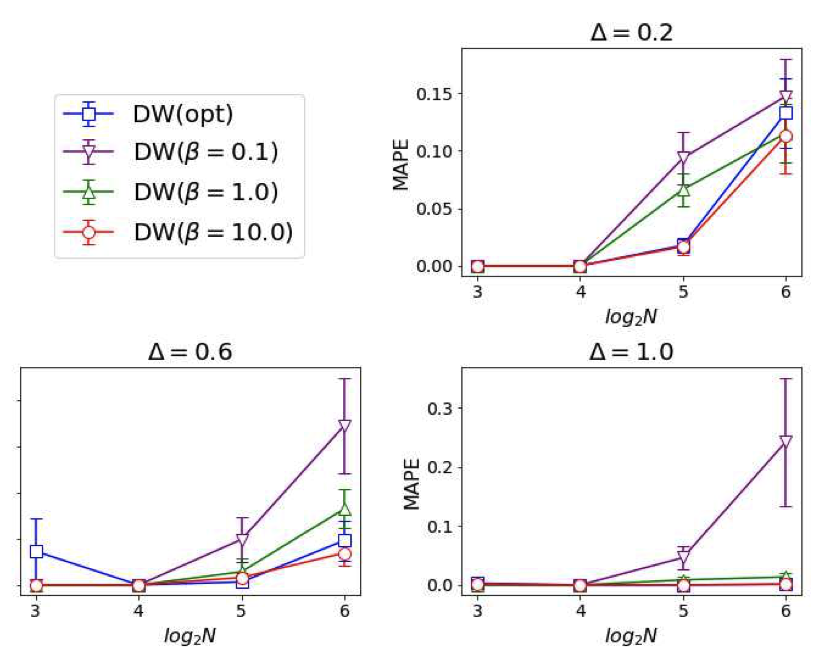
図2. MAPE の $N$ – 依存性 ( https://doi.org/10.48550/arXiv.2012.06119 )。
図 2 から、$N=64$ までの全てのインスタンスで実行可能解が得られていることが分かります。スラック変数を使用した場合、スラック変数の追加により、D-Wave 2000Q では $N=64$ の問題を解くことができません。したがって、本アルゴリズムは D-Wave 2000Q において、スラック変数を用いる以前の手法よりも大きなサイズの問題を扱えることが分かりました。
また、$\Delta=0.2$ のとき、$N$ が増加すると 4 つのモード全てにおいて MAPE が増加していることが分かります。一方、$\Delta=0.2$ では、DW(β = 0.1) を除き、$N$ が増加しても MAPE はほぼゼロに近い値を維持しています。このことから、QKP のグラフが密であるほど、本アルゴリズムによって実行可能解を正確に求められることが分かります。
4 つのモードを比較すると、DW(opt) および DW(β = 10.0) が $\Delta$ の値に関わらず正確な解を出しています。したがって、QKP では DW(opt) もしくは DW(β = 10.0) を使用することが良いと考えられます。また、DW(β = 0.1) では例外的に MAPE が大きくなっていることから、サンプリングモードにおける β の調整は重要であると言えます。
計算時間の検証
本アルゴリズムと Gurobi オプティマイザの計算時間を比較します。比較対象の時間をそれぞれ以下のように定義します。
- $t_{\rm QA}$ : D-Wave 2000Q に搭載された量子デバイスへの総アクセス時間 ( すなわち QA の合計時間 )
- $t_{\rm sampling}$ : インターネットの遅延や $t_{\rm QA}$、D-Wave 2000Q での他の処理を含む総サンプリング時間
- $t_{\rm unemb}$ : unembedding ( アルゴリズムの手順 4. ) にかかった合計時間
- $t_{\rm ADMM}$ : 本アルゴリズムによる総計算時間 ( すなわち $t_{\rm QA}$、$t_{\rm sampling}$、$t_{\rm unemb}$ などの処理の総和 )
- $t_{\rm Gurobi}$ : Gurobi オプティマイザによる総計算時間
それでは、$\Delta=0.2, 0.6, 1.0$ における各計算時間の $N$ – 依存性を以下の図 3 に示します。
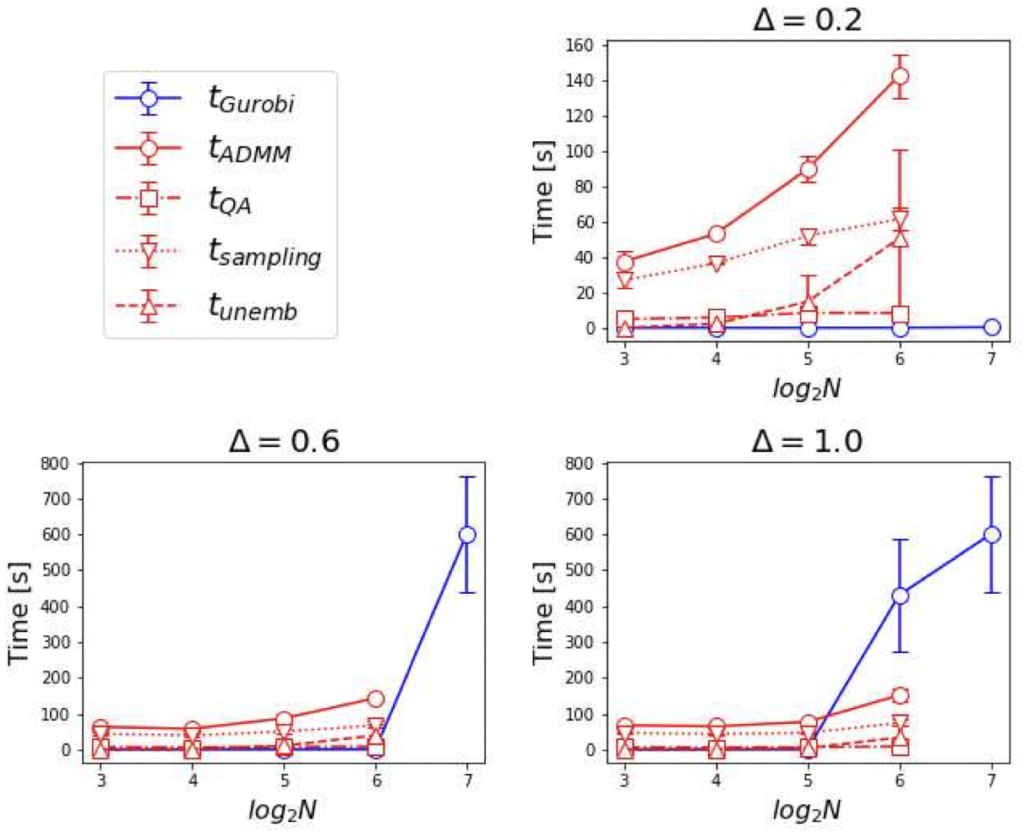
図3. $\Delta=0.2, 0.6, 1.0$ における計算時間の $N$ – 依存性 ( https://doi.org/10.48550/arXiv.2012.06119 )。
赤丸 ( $t_{\rm ADMM}$ ) と青丸 ( $t_{\rm Gurobi}$ ) は、それぞれ DW(β = 10.0) と Gurobi オプティマイザを用いて得られたインスタンス平均の計算時間です。この図から、$ \Delta = 0.2, 0.6$ では、Gurobi オプティマイザは ADMM より大幅に高速であることが分かります。しかし、$t_{\rm Gurobi}$ は $\Delta$ と $N$ の増加に伴い劇的に増加し、$\Delta=1.0$、$N=64$ では $t_{\rm ADMM} < t_{\rm Gurobi}$ となっています。したがって、本アルゴリズムは $\Delta$ および $N$ の増加に伴い Gurobi オプティマイザよりも高速になる可能性があります。
また、$t_{\rm sampling}$ および $t_{\rm unemb}$ は が大きくなると増加しますが、$t_{\rm QA}$ はほぼ一定です。したがって、$t_{\rm sampling}$ や $t_{\rm unemb}$ のような計算オーバーヘッドを削減すれば $t_{\rm ADMM}$ はより高速になり得ます。したがって、よりサイズが大きく密なグラフを実装した量子アニーリングマシンが開発され、もはや embedding や unembedding が必要無くなれば、本手法は高速化すると予想されます。
結論
本論文では、D-Wave 2000Q を用いた不等式制約付き二値最適化問題の新しい解法を提案しました。具体的には、拡張ラグランジュ法を用いて新たなコスト関数を定義し、QA と ADMM を組み合わせたハイブリッドアルゴリズムを開発しました。
本アルゴリズムの性能を QKP に対して検証した結果、スラック変数を用いる従来の手法では計算できない大規模な問題に対して、実行可能解を求めることができました。そして、問題のグラフが密であるほど、より正確な実行可能解が得られました。また、本アルゴリズムに適した後処理は、最適化モードあるいは $\beta = 10.0$ のサンプリングモードであることが分かりました。さらに、計算時間について検証した結果、QKP がサイズの大きな密グラフで与えられる場合、本アルゴリズムは Gurobi オプティマイザよりも高速に計算できることが分かりました。一般に、疎グラフに比べて密グラフの方が解くことが難しいため、密グラフについて正確な解を高速に得られる点も、本アルゴリズムの長所であると言えます。
あと書き
スラック変数なしで不等式制約を緩和するために階段関数を使い、さらに階段関数が QUBO 形式にできない問題を ADMM で解消している点が巧妙だなと感じました。
本論文のアルゴリズムによって、スラック変数を用いる従来手法では解けなかった問題サイズに対応できることは分かりましたが、従来手法で解ける問題サイズにおいて本アルゴリズムと解の精度を検証した場合には、どのような結果が得られるかが気になりました。
また、本アルゴリズムは D-Wave 2000Q が確率的に解を出力する性質を用いていますが、リバースアニーリング[4]を用いて前の反復での解を初期解とした場合に、本アルゴリズムによって得られる解の精度や収束の速さにどのような違いが現れるのかについて興味を持ちました。
補足
補足 1 : embedding と unembedding
ここでは、D-Wave マシンによる最適化で重要な役割を果たしている embedding と unembedding について説明します。
密グラフと疎グラフ
D-Wave マシンは、QUBO あるいはイジングモデルの最小化問題を近似的に解きます。QUBO とイジングモデルの最小化問題は、QUBO の二値変数 $x_i \in \{ 0, 1\}$ とイジングモデルのスピン変数 $s_i \in \{ -1, +1\}$ について $s_i = 2 x_i -1$ という変数変換を行うことにより、等価な最適化問題であることを示すことができます[1]。したがって、以降はイジングモデルを中心に説明を進めます。イジングモデルは、以下の式で表されます。
$$ \frac{1}{2} \sum_{i \ne j} J_{ij} s_i s_j + \sum_{i=1}^{N} h_i s_i $$
このイジングモデルは、スピン変数 $s_i$ をノード、相互作用 $J_{ij}$ をエッジの重み、磁場 $h_i$ をノードの重みとするグラフで表すことができます。D-Wave マシン上で最適化問題を解くためには、このグラフを D-Wave マシン上に実装されているハードウェアグラフに当てはめる必要があります。このハードウェアグラフ上では、物理量子ビットがノードにあたります。そして、量子ビット同士が回路上で結線された所がエッジとなります。しかし、全ての量子ビットが互いに結合しているわけではありません。物理的な回路として実装する以上、量子ビット同士を結線できるのは、互いに近接している箇所に限られます。このようなノード同士の結合が少ないグラフのことを「疎」グラフと呼びます。
一方で、ノード同士の結合が多いグラフのことを「密」グラフと呼びます。最も密なグラフは、全てのノード同士がエッジでつながっているグラフです。そのようなグラフは「完全グラフ」と呼ばれます。以下の図 4 に、疎グラフと密グラフ ( 完全グラフ ) の例を示します。
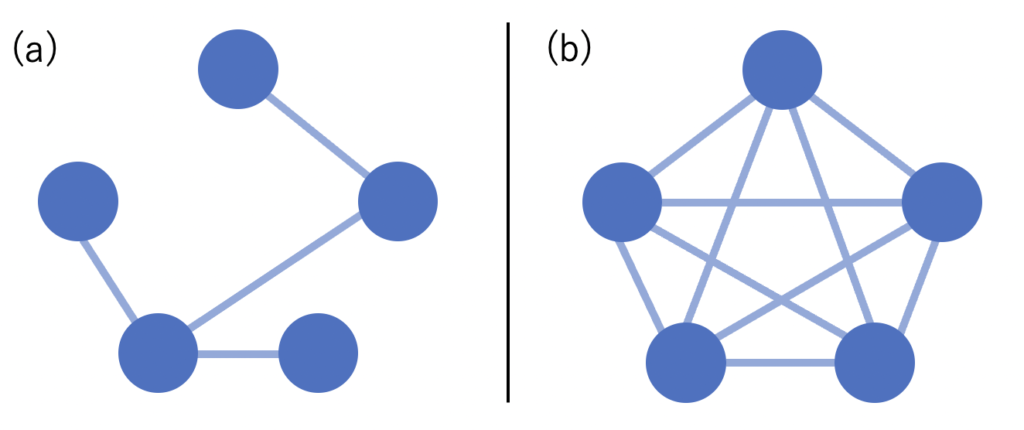
図4. (a) 疎グラフと (b) 密グラフ (完全グラフ) の例。
embedding
解きたい問題に対応するイジングモデルが疎グラフであれば、そのままハードウェアグラフに入力することができますが、密グラフであった場合には、何らかの工夫をして疎な結合のハードウェアグラフに埋め込む必要があります。D-Waveマシンには、この「埋め込み」を実現する技術が備わっており、embeddingと呼ばれています。すなわち、embedding は「イジングモデルのスピン変数 → 量子ビット への置換」を行う処理にあたります。
embedding の一例を示します。解きたい問題に対応するイジングモデルが上図 4(b) のグラフ ( 5 ノードの完全グラフ ) で与えられ、ハードウェアグラフが以下の図 6 で与えられていたとします。このグラフはキメラグラフと呼ばれ、D-Wave 2000Q のハードウェアグラフの単位構造 ( ユニット・セル ) として採用されています。
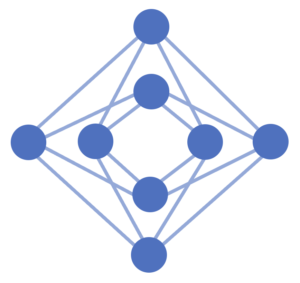
図5. D-Wave マシン上のハードウェアグラフの一例 (キメラグラフ)。
しかし、図 4(b) のグラフは全結合グラフなのに対し、図 5 のキメラグラフは疎グラフであるため、イジングモデルのノード ( スピン変数 ) をキメラグラフのノード ( 量子ビット ) に一対一で割り当てることはできません。この問題を解決するために、embedding では 1 つのスピン変数を複数の量子ビットに割り当てます。ただし、それらの量子ビットは同一のスピン変数を表すため、同じ向きを取るように制御する必要があります。このような、量子ビットからなるブロックをチェーン ( Chain ) と呼びます。チェーンの導入により、5 ノードの完全グラフはキメラグラフ上に以下のように埋め込むことができます。
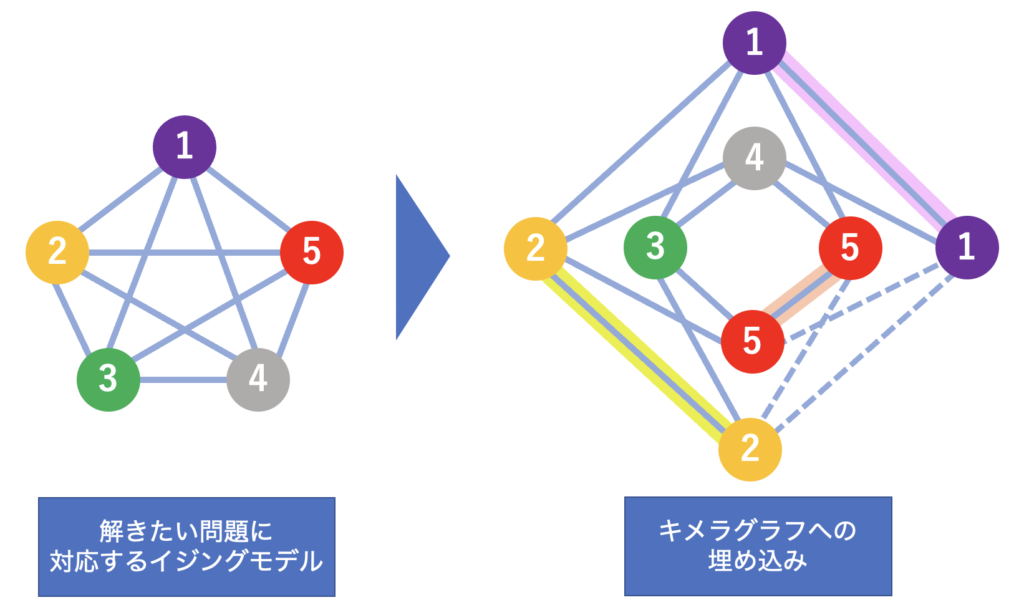
図6. チェーンを用いた埋め込みの一例 ( 点線は使われていないエッジ )。
図 6 に示した埋め込みでは、ノード 1, 2, 5 をチェーンにしています。これにより、5 種類のノード全てを他の 4 種類のノードと結合させ、擬似的に全結合を再現することができました。[3]
unembedding
量子アニーリングを実行した後、ハードウェアグラフ上の各量子ビットは +1 か -1 に対応するいずれかの状態を取りますが、それをイジングモデルのスピン変数に戻すことによって、解きたい最適化問題の解が得られます。この「量子ビット → イジングモデルのスピン変数への置換」という embedding と逆の処理を unembedding と呼びます。unembedding には、チェーンにおいて本来は同じ値を取るべき量子ビットが異なる値を取ってしまった場合 ( これをチェーンブレーク ( chain break ) と言います ) などに、どちらの値を採用するかを決定する処理が含まれます。デフォルトでは、チェーンの中で、その向きを取っている量子ビットが多い方を採用する「多数決法」が設定されています。また、他には「エネルギー最小化法」と呼ばれるものがあります。この方法では、局所的なコスト関数を最小化することによって、より低いエネルギーのサンプルが得られるようにしています。
補足 2 : スラック変数の二値変数による展開
3. 課題 にて、式 (4) のスラック変数 $s_m$ は $s_m= 2^{0} \times y_1 + 2^1 \times y_2 + 2^2 + y_3 + \cdots $ というように補助的な二値変数 $y_1, y_2, y_3, \cdots$ で表現し直す必要があると述べました。このことを簡単な例で確認していきます。
今、不等式制約の数が一つ ( すなわち $M=1$ ) であるとします。したがって、不等式制約 $ {\bm G}^{\top} _m {\bm x} \leq D_m \ (m=1,\cdots,M)$ の添え字 $m$ は省略します。そして、$N=3$、${\bm G} = [1,2,2]^{\top}$、${\bm x}=[x_1, x_2, x_3]^{\top}$、$D=3$ であるとします。このとき、不等式制約 ${\bm G}^{\top} {\bm x} \leq D$ は以下のようになります。
$$ x_1 + 2 x_2 + 2 x_3 \leq 3 \tag{*} $$
この不等式を式 (4) の罰金項にしてみると、
$$ (x_1 + 2 x_2 + 2 x_3 – 3 + s)^2 \tag{**} $$
となります。このとき $s$ がとり得る値は $\{ 0,1,2,3\}$ にする必要があります。このことは、以下の表から確認できます。表中の $s^{\ast}$ は、式 (**) を 0 にする $s$ の値、すなわち $s^{\ast} = – (x_1 + 2 x_2 + 2 x_3 – 3)$ です。この表から、$s^{\ast}$ が負のときにのみ不等式 (*) に反していることが分かります。従って、$s^{\ast}$ が $0,1,2,3$ の値を取れるようにすれば、不等式 (*) を満たす時にのみ罰金項 (**) が 0 になるように $s$ でカバーすることができます。
| $x_1$ | $x_2$ | $x_3$ | $x_1 + 2 x_2 + 2 x_3 – 3$ | $s^{\ast}$ |
| 0 | 0 | 0 | -3 | 3 |
| 0 | 0 | 1 | -1 | 1 |
| 0 | 1 | 0 | -1 | 1 |
| 0 | 1 | 1 | 1 | -1 |
| 1 | 0 | 0 | -2 | 2 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 2 | -2 |
以上より、不等式 (*) を満たすには $s \in \{ 0,1,2,3\}$ とすれば良いことが分かりました。$s$ のとり得る値の上限 ( ここでは 3 ) は $D$ に対応する値であるため、一般には $s \in \{ 0,1,\cdots,D \}$ とします。
さて、ここでは $s \in \{ 0,1,2,3\}$ とすれば良いことが分かりましたが、QUBO 問題は「二値」最適化問題であるため、$s$ を二値変数で表し直す必要があります。具体的には、新たな変数 $y_1,y_2 \in \{ 0, 1\}$ を用いて $s=2^0 \times y_1 + 2^1 \times y_2$ とすることにより、$s$ はちょうど $0,1,2,3$ の値をとれるようになります。
| $y_1$ | $y_2$ | $s$ |
| 0 | 0 | 0 |
| 0 | 1 | 2 |
| 1 | 0 | 1 |
| 1 | 1 | 3 |
また、$D=2$ の時には、先ほどの議論から $s \in \{ 0,1,2 \}$ とすれば良いわけですが、二値変数 $ y_1, y_2 \in \{ 0, 1\}$ で $s_m=2^0 \times y_1 + 2^1 \times y_2$ とすると、上の表が示すように $y_1=y_2=1$ のときに $s=3$ をとってしまいます。このような場合には $y_1=y_2=1$ にならないように $y_1 \times y_2$ という罰金項を、適切な罰金係数を掛けた上で目的関数に足すことで対処されます。
参考文献
-
T-Wave用語集 イジング模型とQUBO : /T-Wave/?p=2325
-
D-Wave ドキュメント 後処理モード D-Waveシステムの後処理方法 :
https://dwavejapan.com/app/uploads/2020/02/09-1105A-H_J-DeveloperGuidePostProcessing.pdf
-
NTTデータ量子コンピューティングガイドライン 量子アニーリングマシン/イジングマシン編 2021年 1月:
https://www.nttdata.com/jp/ja/-/media/nttdatajapan/files/news/services_info/2021/012800/012800-01.pdf -
T-Wave用語集 リバースアニーリング:/T-Wave/?p=2306