文献情報

• タイトル: Traffic Flow Optimization Using a Quantum Annealer
• 著者: Florian Neukart, Gabriele Compostella, Christian
  Seidel, David von Dollen, Sheir Yarkoni and Bob Parney
• 書誌情報: Frontiers in ICT 4, 29 (2017). (doi: 10.3389/fict.2017.00029)

概要

交通渋滞を緩和するために複数台の車の経路選択を組合せ最適化問題として定式化し、これをD-Wave 2Xにより解いた。

方法

方針

古典: 現時点の位置から目的地までの経路を各車両ごとに3つ用意する
量子: 各車両の取る経路を目的関数を最小化するように選択する

最適化問題の定式化

組合せ最適化問題の種類: 二値整数線型計画問題
変数: $q_{ij} \in \{0, 1\}$ (車$i$が経路 $j \in {1, 2, 3}$を取れば$1$, そうでなければ$0$)
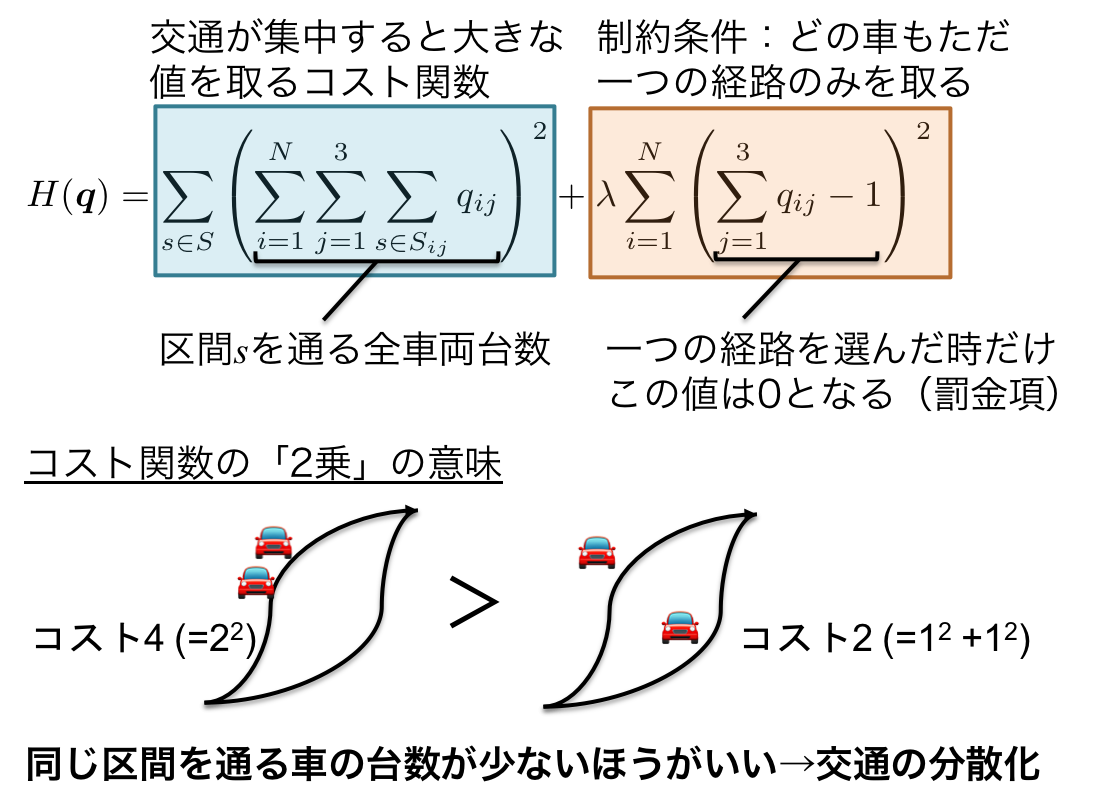
目的関数:

用いたデータセット

公開データセットのT-Drive trajectory datasetの中から、北京の街の中心と北京空港の間を行き来する418台の車のGPSデータを今回の問題の対象として抽出した。また、OSMnxというツールを用いて北京の街の地図から交差点をノード、その間を繋ぐ道路をセグメントとして抽出し、先述のGPSデータをそれらの上にマッピングしたものを入力データとした。

D-Waveマシン実装上の工夫

最適化変数の数 = 1,254変数（=418台×3経路）

1,024量子ビットのD-Wave 2Xではこの数の二値変数を扱うことができない。qbsolvライブラリを用いた逐次最適化を用いた。

論文の結果

D-wave 2X (qbsolv)を用いて解いた結果を元に車の位置の再配置を行った。車が通る全ルートの中での各セグメントの登場回数を混雑度の指標とし、この回数が10回を超えるセグメントを混雑している道路として、その数を用いて結果を評価した。その結果、混雑している道路の数は元々の入力データやランダムに車を再配置した場合に比べて有意に改善されていることが確認できた。

また、計算は50回行ったが、qbsolvにデータを入力してからD-Wave 2Xで計算された結果が帰ってくるまでの時間の中で最小のものはクラウドや処理待ちによる影響が最も小さいと考え、計算時間を計測すると、22秒という結果が得られた。

本記事の担当者

鈴木海渡（編集：観山正道）