文献情報
- タイトル: Ising formulations of many NP problems
- 著者: Andrew Lucas (Google Scholar)
- 書誌情報: Frontiers in Physics 2, 5 (2014). (doi: 10.3389/fphy.2014.00005)
- 親ページ: “Ising formulations of many NP problems” by Andrew Lucas (2014)
- 章タイトル: 5.2. Knapsack with Integer Weights
概要
組合せ最適化問題の類型のひとつにナップサック問題がある。これをIsing模型(変数が1 or -1)と等価な形式であるQUBO形式(変数が1 or 0)によって表現した。
ナップサック問題とは
導入
ナップサック問題にはいくつかの種類があるが、今回扱うのは以下のような形式の問題である。
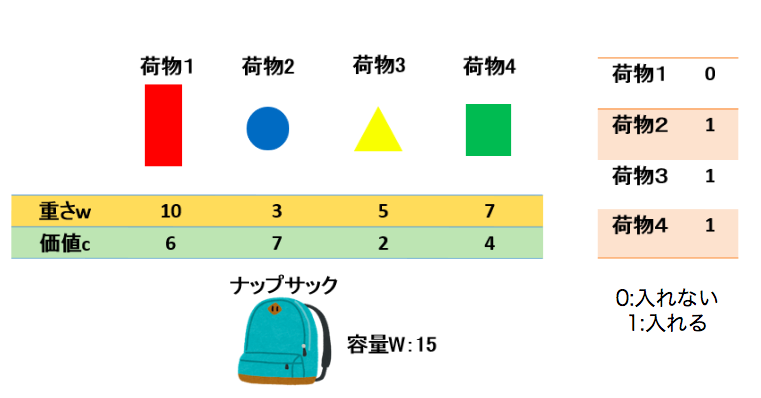
いま、N個の荷物(荷物1、荷物2、・・・荷物N)をがあり、それぞれの荷物についてその荷物の「重さ」と「価値」が分かっているとする。これらの荷物をナップサックに詰め込んで運びたいが、ナップサックには容量があるので持っていく荷物の重さの合計はこの容量を越えてはならない。この条件の下、持っていく荷物の価値の合計を可能な限り大きくするにはどの荷物を持っていくのが良いか?
QUBO表現による定式化
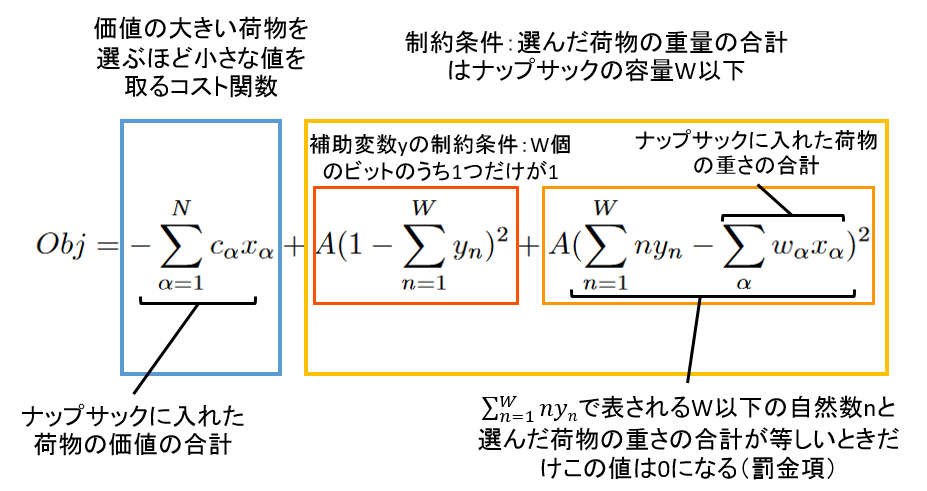
適化変数: $x_{\alpha} \in \{0,1\}$ (荷物$\alpha$をナップサックに入れれば$1$,入れなければ$0$)
補助変数: $y_n$ (自然数$m$を表すとき左から$m$番目の$y_m$が$1$,それ以外の全ての$y_{n (n\neq m)}$は$0$)
目的関数:

本記事の担当者
鈴木海渡