文献情報
- タイトル:Path Integral Monte Carlo Quantum Annealing-based Clustering and Routes Optimization of Clustered UAV Network
- 著者:Chongle Zhang, Changhua Zhu, Yuxin Li, Min Ni, Yunpeng Zhu
- 書誌情報:https://doi.org/10.1109/PAAP54281.2021.9720448
概要
無人航空機(以下UAV)は他のUAVや管制室と通信する際にエネルギーを消費します。UAVがどのUAVや管制室と通信を行うかを表したものを無線通信網と呼びますが、消費するエネルギーが小さくなるような無線通信網を作成します。この論文では量子アニーリングをシミュレーションする手法である量子モンテカルロ法によって無線通信網を作成するアルゴリズムを提案しました。また実験では最適化手法の一つであるSimulated Annealing(以下SA)で作成した場合との比較を行います。実験の結果、量子モンテカルロ法ではSAのときよりも消費するエネルギーが小さい無線通信網を作成することができました。
背景・課題
UAVとはドローンのような人間が搭乗せずに管制室などと通信しながら飛行する航空機を指します。現在UAVは軍事・農業といった様々な分野で広く使われています。一方でUAVは通信する際にエネルギーを消費するため、エネルギー消費量の小さい通信網を作成することが重要になります。この通信網の作成は組合わせ最適化問題として表すことができ、組合わせ最適化問題を解くために使われるアルゴリズムにSAがあります。携帯電話や乗用車についての通信網の作成をSAで行った先行研究はありますが、SAでは十分にエネルギー消費量が小さい解を得られない可能性があります。一方で量子モンテカルロ法はSAと比較すると最適な解を得られることが期待される最適化手法であり、SAよりもエネルギー消費量が小さい無線通信網を作成できる可能性があります。そこで本論文では量子モンテカルロ法により無線通信網を作成し、SAとの比較を行います。
方法
目標はエネルギー消費量が最も小さい無線通信網を得ることです。このためにどのUAV間同士で通信を行うかを求めます。
グラフへの変換
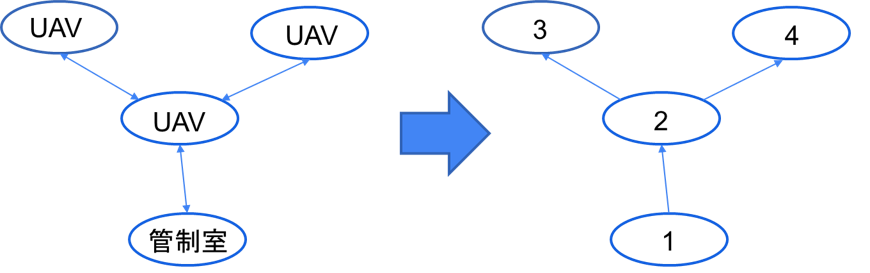
まず管制室とUAVを頂点、通信における送受信の関係を辺、その辺の重みをUAV同士で通信する際に消費されるエネルギー量とみなすことで無線通信網を有向グラフとして表現します。図1に例を示しました。ここで頂点1は管制室を表します。有向グラフで考えることで、UAV間の通信を有向グラフ上の辺として考えることができます。
定式化
まず二値変数として$s_{i,j}$を定義します。これは頂点$i$から頂点$j$に辺を生やすときに1、そうでないときに0となる変数です。
目的関数
実際に通信が行われるUAV間で消費されるエネルギー量の総和、つまり有向グラフの辺の重みの総和を最小化します。これは以下の(1)式のように定式化することができます。ここで$w_{i,j}$は頂点$i$から頂点$j$を結ぶ辺の重みを表します。
$$
H_{0}=\sum_{i,j} w_{i,j} s_{i,j} \tag{1}
$$
辺の重み$w_{i,j}$は以下の(2)式で表されます。$d_{i,j}$はUAV同士の距離を表します。$E_r$は無線通信を行うためのUAVの機器に必要なエネルギー量を表す定数、$\varepsilon_{\text{f}_\text{s}}$、$\varepsilon_{\text{mp}}$は通信距離に対するコストを表す定数、$d_0$は距離についてのしきい値です。今回はこれらの具体的な値は$E_r=50 \mathrm{nJ/bit}$、$\varepsilon_{\text{f}_\text{s}}=10\mathrm{pJ/bit/m^2}$、$\varepsilon_\text{mp}=0.0013\mathrm{pJ/bit/m^4} $、$d_0=87.7\mathrm{m}$としました。
$$
w_{i,j}=E_s(d_{i,j})
=\left\{
\begin{array}{ll}
E_r + \varepsilon_{\text{f}_\text{s}} d_{i,j}^2 & d_{i,j} \leq d_0 \\
E_r + \varepsilon_\text{mp} d_{i,j}^4 & d_{i,j} > d_0
\end{array}
\right.
\tag{2}
$$
制約項
実際に利用できる無線通信網を作成するためにはUAVの性能によるいくつかの制約があります。この制約を制約項として最小化問題に定式化します。
制約項1
すべてのUAVは他のUAVや管制室と通信を行いながら飛行します。そこでどのUAVも他のUAVまたは管制室のうちどれか一つから情報を受信する制約を加えます。ここでそれぞれのUAVにつき受信源は1つあれば十分であり、2つ以上のUAVから受信することは消費するエネルギー量が増加するため不要です。これを有向グラフで考えるとどの頂点も他の頂点から入る辺が1本だけあるという制約です。これは以下の(3)式のように定式化されます。ここで$B$は頂点数を表します。
$$
H_1=\sum_{j=2}^B \left(\sum_{i} s_{i,j} – 1\right)^2 \tag{3}
$$
$\sum_{i} s_{i,j}$は頂点$i$に入る辺数を表します。制約を満たして頂点$i$に入る辺の数が1のとき$(\sum_i s_{i,j} – 1)^2 = 0$となり最小となります。
制約項2
UAVは機体の性能上の問題により通信を行うことができるUAVの数に制限があります。このためUAVが一定の数を超えるUAVと通信を行わないという制約を加えます。これを有向グラフで考えると各頂点から出る辺数に制限があることを表します。
頂点から出る辺の数に対する制約の定式化について考えます。まず$\sum_j s_{i,j}$は頂点$\j$から出る辺数を表しています。頂点から出る辺数が$\Delta$本以下であるときは$\sum_j s_{i,j} – 1$が$\sum_j s_{i,j} -1$ と$\Delta-1$の小さい方と一致します。なぜなら頂点から出る辺数が$\Delta$ 本以下であるときは$\sum_j s_{i,j} – 1 \leq \Delta – 1$であるので$\sum_{j} s_{i,j}-1 = \min(\sum_{j} s_{i,j}-1, \Delta – 1)$となりますが、頂点から出る辺数が$\Delta$本より多いときは$\sum_{j}s_{i,j}-1>\Delta-1$であるので$\min(\sum_j s_{i,j} -1, \Delta -1)=\Delta – 1$となり、$\sum_{j} s_{i,j} -1$と一致しなくなるからです。つまり制約を満たすためには管制室以外の頂点$2 \leq i \leq B$ について$\sum_{j} s_{i,j}-1 = \min(\sum_{j} s_{i,j}-1, \Delta – 1)$を満たす必要があります。
そこで$\min(\sum_{j} s_{i,j}-1, \Delta – 1)$を表すために$E_{i,e}$を導入します。$E_{i,e}$の定義は以下の(5)式で表されます。
$$
E_{i,e} = \left\{
\begin{array}{ll}
0 & e \geq \sum_j s_{i,j}\\
1 & e < \sum_j s_{i,j}
\end{array}
\right.
\tag{5}
$$
それぞれの$e$の値に対する$E_{i,e}$の値と、$\Delta < \sum_j s_{i,j}$、$\sum_j s_{i,j} \leq \Delta$ それぞれのときの$\sum_{e=1}^{\Delta-1} E_{i,e}$の値を図2に示しました。図2から$\sum_{e=1}^{\Delta-1} E_{i,e} = \min(\sum_j s_{i,j} – 1, \Delta – 1 )$となることが確認できます。
以上より制約項2の定式化は以下の(4)式で表されます。ここで$\Delta$は頂点から出ることのできる最大の辺数を表します。
$$
H_2 = \sum_{i=2}^B \left(\sum_{j} s_{i,j} – \sum_{e=1}^{\Delta – 1} E_{i,e} \right)^2 \tag{4}
$$
制約を満たすように頂点から出る辺数が$\Delta$本以下であるとき、つまり$\sum_j s_{i,j} \leq \Delta$のときは$(\sum_j s_{i,j} – \sum_{e=1}^{\Delta-1} E_{i,e})^2 = (\sum_j s_{i,j} – (\sum_{j} s_{i,j} – 1))^2=1$となり最小となります。
なお論文ではこの制約項について頂点から出る辺数を$\Delta – 1$本以下に制限するとありましたが、これは$\Delta$ 本以下の誤りであると考えられます。頂点から出る辺の本数がちょうど$\Delta$本のとき$\sum_{j} s_{i,j} = \Delta$であるから$\sum_{e=1}^{\Delta-1} E_{i,e} = \sum_j s_{i,j} – 1$となり、このときは$(\sum_{j} s_{i,j} – \sum_{e=1}^{\Delta-1} E_{i,e})^2$は最小値である1をとり、(4)式の定式化では頂点から出る辺の本数がちょうど$\Delta$本のときは制約を満たすと解釈できるからです。
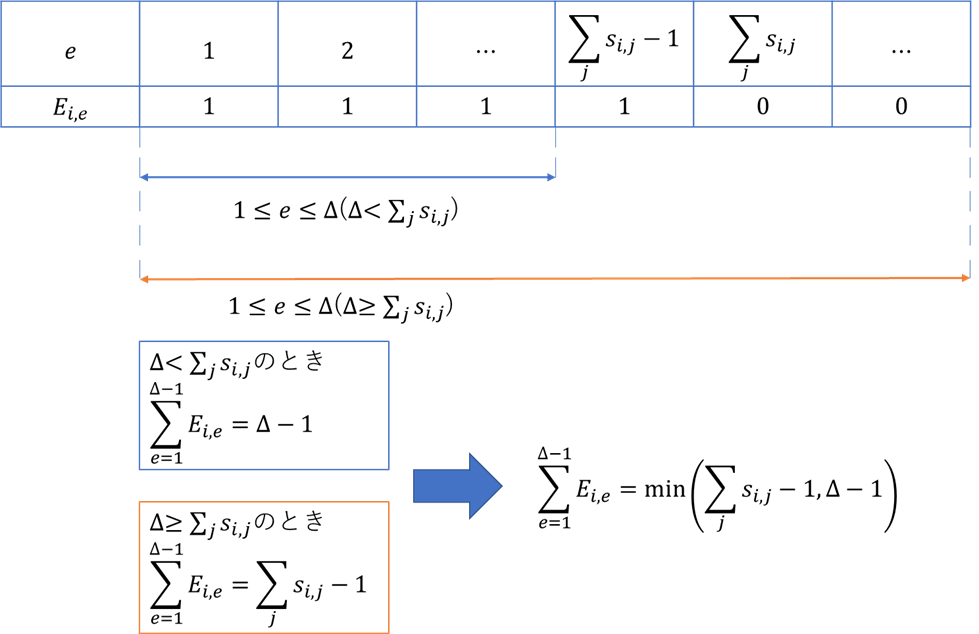
 $e$の値に対する$E_{i,e}$と$\sum_{e=1}^{\Delta-1}E_{i,e}$の値
$e$の値に対する$E_{i,e}$と$\sum_{e=1}^{\Delta-1}E_{i,e}$の値制約項3
最後に三つ目の制約項です。管制室が航空を制御するためにはUAVによる情報の送信を制限する必要があります。そこで送信を行うUAVの個数を制限する制約を加えます。
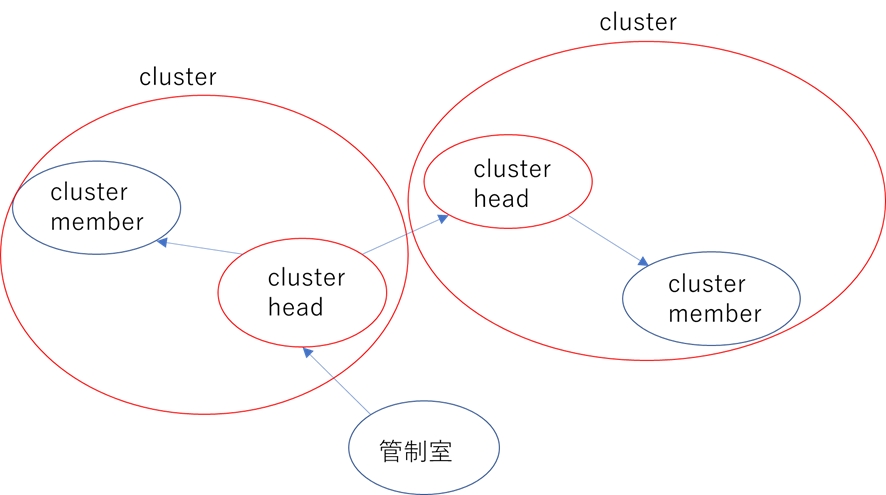
他のUAVへ送信を行うUAVをcluster head、cluster headから情報を受け取るUAVをcluster member、1つのcluster headとcluster memberで構成されるUAVの集合をclusterと呼びます。図3にUAVをcluster memberとcluster headに分類した例を示しました。図3のように無線通信網はいくつかのclusterに分けることができ、clusterの個数はcluster headの個数に一致します。
本論文ではこの制約によりclusterの個数を$C_{num}$個に制限します。有向グラフで考えるとcluster headを表す頂点はその頂点から出る辺が1本以上あることを表すので、この制約は出る辺が1本以上ある頂点を$C_{num}$個にする制約になります。この制約の定式化は以下の(6)式となります。
$$
H_3 = \left(\sum_{i=2}^B \left(\sum_{j=2}^B s_{i,j} -\sum_{e=1} E_{i,e}\right) – C_{num}\right)^2 \tag{6}
$$
この定式化について説明します。まず$E_{i,e}$は前述のとおりです。頂点から出る辺数が0すなわち$\sum_{j} s_{i,j} = 0$のとき、$e \geq 1$で$E_{i,e}=0$となるので$\sum_{e} E_{i,e} = 0$となります。一方頂点から出る辺数が1以上すなわち$\sum_{j} s_{i,j} \geq 1$のとき、$1 \leq e \leq \sum_{j} s_{i,j} – 1$で$E_{i,e}=1$、$\sum_{j} s_{i,j} \leq e$で$E_{i,e}=0$となるので$\sum_{e} E_{i,e}=\sum_{j} s_{i,j} – 1$となります。つまり頂点から出る辺数が1以上のとき$\sum_{j} s_{i,j} – \sum_{e} E_{i,e}=1$となります。以上より$\sum_{i=2}^B (\sum_{j=2} s_{i,j} – \sum_{e=1}E_{i,e})$が頂点から出る辺数が1以上のとなる頂点の数を表しています。cluster headとなる頂点の個数が$C_{num}$個のとき$H_3$は最小となります。
これらの目的関数と制約項によりコスト関数は以下の(7)式のようになります。ここで$w_{\max}$は辺の重みで最大のものを表します。$H_1$~$H_3$が最小とならないときは$w_{\max}$を係数にかけているためコスト関数は最小となりません。
$$
H_0 + w_{\text{max}} ( H_1 + H_2 + H_3) \tag{7}
$$
量子モンテカルロ法
量子アニーリングによって無線通信網を作成すると、SAを利用した時よりも通信網のエネルギー量が小さくなることが期待されます。量子アニーリングでは最適化問題をQUBO形式に表す必要があります。QUBOとは以下の(8)式の形式で表される式のことです。ここで$x_{i} \in \{0, 1\}$は二値変数を表します。
$$
QUBO = \sum_{i} \sum_{j} Q_{ij} x_{i} x_{j} \tag{8}
$$
しかし(4)式、(6)式で用いた変数$E_{i,e}$をQUBO形式で表すことが困難です。そこで本論文では量子モンテカルロ法により最適化を行います。
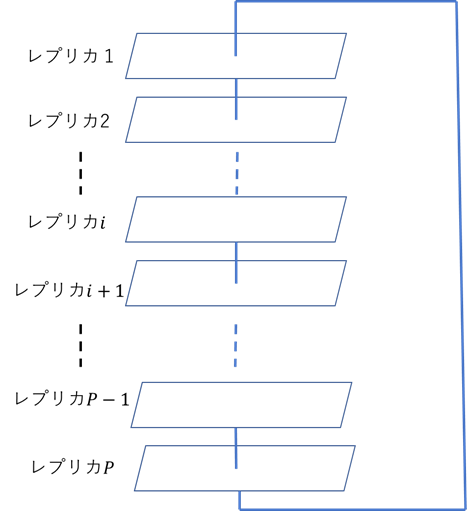
量子モンテカルロ法は量子アニーリングを古典コンピュータ上でシミュレーションしたものとなります。量子アニーリングは最適化問題を表す古典イジング模型に横磁場の影響を加えて最適化問題の解を探索します。古典コンピュータではこの古典イジング模型と横磁場を直接分割して表現することは困難ですが、十分に大きな個数の古典的なイジング模型を用いることでシミュレーションすることが可能になります。ここで用いる古典イジング模型の個数を$P$として、そのうち$i$番目のものをレプリカ$i$と呼ぶことにします。図4に$P$個のレプリカを用いる様子を示しました。図4のように量子モンテカルロ法におけるハミルトニアンは$P$個のレプリカを用いることによって次元が1つ増えています。
横磁場の影響は隣り合ったレプリカの相互作用によって近似的に表すことができます。具体的には以下の(9)式によって横磁場の影響を表現することができます。
$$
H_k = -J_\Gamma \left( \sum_{z}^{P-1} \sum_{(a, b)} s_{a,b}^{z} s_{a,b}^{z+1} + \sum_{(a, b)} s_{a,b}^{P} s_{a,b}^{1} \right) \tag{9}
$$
$J_\Gamma$は以下の(10)式で表されます。
$$
J_\Gamma = -\frac{T}{2} \log \tanh \frac{\Gamma}{PT} \tag{10}
$$
ここで$\Gamma$は横磁場にかかる係数であり、初めは高い値として状態を更新しながら徐々に小さくします。また$T$は温度を表し、これは十分小さな値をとります。
量子モンテカルロ法における最適化問題を表すコスト関数は上記に示した(7)式を$P$個のレプリカそれぞれについて計算し、その平均をとった以下の(11)式で表されます。
$$
H_P =\frac{1}{P} \sum_{z=1}^{P}(H_0 + w_{\max}(H_1 +H_2 + H_3)) \tag{11}
$$
以上より量子モンテカルロ法におけるコスト関数は以下の(12)式で表されます。
$$
H_c = H_p + H_k \tag{12}
$$
$\Gamma$を小さくすると$J_\Gamma$の値は大きくなるため、状態を更新するにつれ(12)式の第二項の影響が$P$個の解を等しくするように強まります。複数の解を用いて解の候補を増やすことでエネルギーが低くなる状態を探しやすくし、さらに複数の解が一つに近づくようにすることができます。
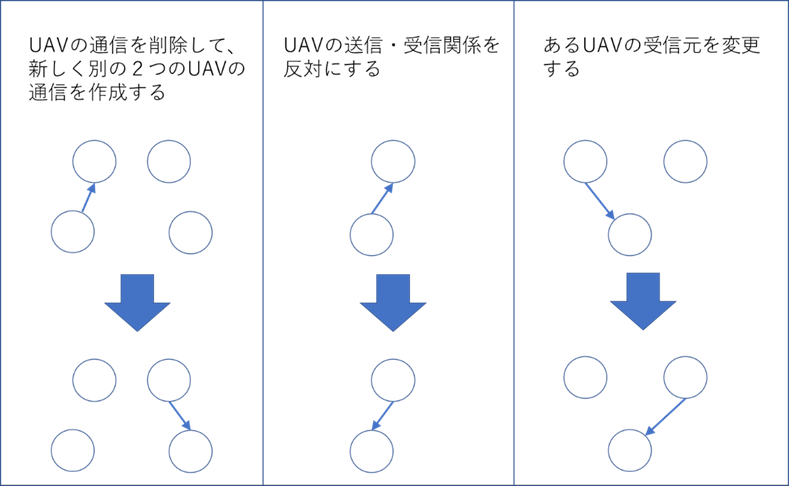
量子モンテカルロ法ではレプリカそれぞれについて解を変化させます。このとき解を変化させる方法は以下の3つです。また図5にこの3通りの変化の例を示しました。
- ある2つのUAVの通信を削除して、新しく別の2つのUAVの通信を作成する
- UAVの送信・受信関係を反対にする
- あるUAVの受信元を変更する
状態を遷移させるかを決定するためにコスト関数を計算します。変化させる前の状態と変化させた後の状態に対して(11)式の差分を$\Delta H_p$、(9)式の差分を$\Delta H_k$ 、$\Delta H_c = \Delta H_p / P – \Delta H_k$とします。$\Delta H_p < 0$または$\Delta H_c < 0$のときは解を変化させた後の状態に遷移させます。そうでない場合は確率$\exp(-\Delta H_c / T)$で状態を遷移させます。
量子モンテカルロ法では以上の解の変化・遷移を$P$個のレプリカそれぞれに対して行うことを繰り返します。レプリカ1からレプリカ$P$まで解の変化・遷移を行うごとに実際のエネルギー消費量を記録していきます。ここで量子モンテカルロ法では$P$個の解が得られますが、実際に記録する解は$P$個のうち最もエネルギー消費量が小さい解を選択します。
上記をまとめると量子モンテカルロ法は以下のアルゴリズムによって実行されます。
- $P$個のレプリカを用意する。
- レプリカ1について図5の3つの方法のうちどれか1つで解を変化させる。
- レプリカ1の変化させる前と後の状態でコスト関数を計算し、その値によって解を遷移させる。
- レプリカ2~レプリカ$P$について2.、3.を同様に実行する。
- レプリカ1~レプリカ$P$の中で最も小さいエネルギー消費量を記録する。
- (9)式の$\Gamma$の値を更新する。
- 02.~06.を繰り返す。
実験
まず実験を行うための問題を生成します。ここでは管制室が1つ、UAVが49機と設定しました。これらを合計50個の頂点と見なし、それぞれ1000m×1000m×1000mの範囲を持つ3次元座標上に配置します。ここで管制室を表す頂点は(500, 500, 0)の位置に配置し、UAVを表す頂点はランダムな位置に配置します。
量子モンテカルロ法のパラメータは以下の通りにして実験を行います。
- $\Delta=6$
- $C_{num}=20,50,100$
- $P=40$
- $T=0.04$
- $(\Gamma \text{の初期値})=2.5PT=4.0$
量子モンテカルロ法とSAの比較を行います。20回独立に問題の生成、量子モンテカルロ法による通信網作成、SAによる通信網作成を行います。比較の指標にはすべての問題の中で得られたエネルギー消費量の平均値、最小値、最大値を用います。量子モンテカルロ法では上記のアルゴリズムの02.~06.を$10^2$~$10^7$回繰り返すごとにエネルギー消費量の平均値、最小値、最大値を求めます。SAも同様に解の遷移の回数が$10^2$~$10^7$回のときにエネルギー消費量の平均値、最小値、最大値を求めます。
結果
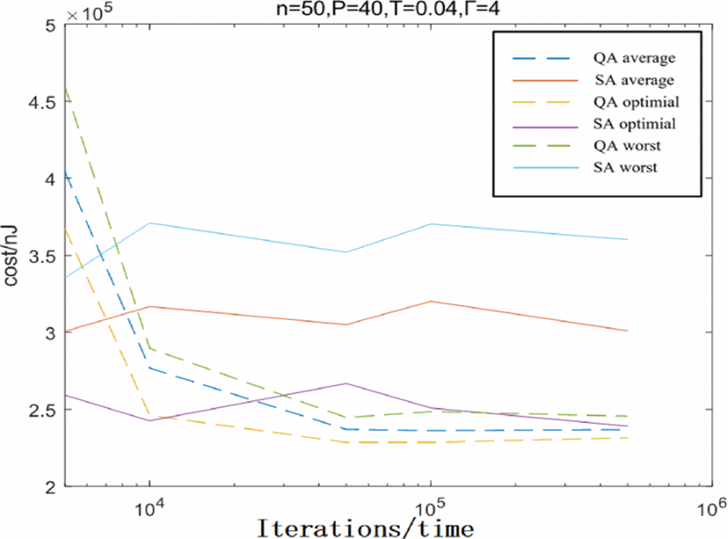
エネルギー消費量の最小値・平均値・最大値のグラフを図6に示しました。QAは量子モンテカルロ法によって作成したときのエネルギー消費量です。初めのうちはSAの方がエネルギー消費量が少なくなっていました。しかし、更新を繰り返すと量子モンテカルロ法が最小値・平均値・最大値のすべてでSAのエネルギー消費量を下回りました。
結論
QAのシミュレーションである量子モンテカルロ法を用いることで、SAよりもエネルギー消費量が小さい通信網を作成することができました。将来的にはD-waveのような量子アニーラを用いて無線通信網の作成実験を行うとしました。
あとがき
通信網の作成を最適化問題として捉えたことやQAを古典コンピュータ上でシミュレーションする部分が面白く感じました。
一方で今回の定式化ではUAVの無線通信網として利用できない解が得られるのではないかと考えました。その例として図7に今回設定した3つの制約を満たす解の一つを示しました。図の例ではUAV同士の間にサイクルが存在しており、かつどのUAVも管制室と通信していません。このような通信網は実際には採用できません。今回の3つの制約に加えて、すべてのUAVが管制室からの情報を受け取るような制約を加えれば対応できると考えました。