文献情報

• タイトル: Analytic and Algorithmic Solution of Random Satisfiability Problems
• 著者: M. Mézard, G. Parisi, R. Zecchina
• 書誌情報: https://www.science.org/doi/10.1126/science.1073287

概要

K-SAT は、いくつかの変数からなる論理式を充足するような真偽値の割当を求める組合せ最適化問題です。K-SAT は $K \ge 3$ のときに NP 完全問題であることが示されており、現在のところ、入力サイズに対して最悪多項式時間で解くアルゴリズムの存在は知られていません。そこで、K-SAT に関して以下の 2 点の研究が進められています。

1. K-SAT の難しさの原因の理解 (計算複雑性理論の観点からの興味)
2. K-SAT を平均的に高速に解くヒューリスティックの開発

本論文では、統計力学、特にスピングラス理論の手法を用いて K-SAT を解析し、上の 2 つの問いに対する洞察を与えます。より具体的には、以下の 2 つの事項について考察します。

1. K-SAT の解空間の構造を調べ、K-SAT の相転移とその原因について考察する
2. K-SAT のインスタンスが与えられたときに、そのインスタンスの解の分布を調べることで、効率的に真偽値の割当を決定するアルゴリズムを構成する

背景

K-SAT とその相転移

K-SAT の詳細な問題設定を述べます。

• 論理変数 $x_1, x_2,\dots,x_N$: $\mathrm{true}$ か $\mathrm{false}$ の2値を取る変数
• リテラル: 論理変数の肯定 $x$ または否定 $\lnot x$
• 節: $K$ 個のリテラルの論理和
• 論理式: $M$ 個の節の論理積

たとえば、 $N=4$ 変数、 $M=3$ 節の 3-SAT のインスタンス (具体的な問題) は以下のような形を取ります。

$$ (x_1\lor x_3 \lor \lnot x_4) \land (\lnot x_1\lor \lnot x_2 \lor x_4) \land (x_2 \lor \lnot x_3 \lor x_4) $$

このようにして与えられる論理式に対して、論理式全体の値を $\mathrm{true}$ にするような各論理変数への論理値の割当を見つけるか、またはそのような割当が存在しないことを報告する問題が K-SAT です。解が存在するとき、そのインスタンスは充足可能、存在しないときは充足不可能であるといいます。例えば、上の例は充足可能であり、 $(x_1,x_2,x_3,x_4)=(\mathrm{true}, \mathrm{false},\mathrm{false},\mathrm{true})$ が解の一つです。

K-SAT のインスタンスに解が存在するか否かは、論理変数の個数 $N$ と節の個数 $M$ の比 $\alpha := M/N$ によって大まかに決定されることが知られています。すなわち、ある臨界値 $\alpha_c$ が存在して、 $\alpha < \alpha_c$ ではほとんどのインスタンスが充足可能、 $\alpha > \alpha_c$ ではほとんどのインスタンスが充足不可能となります。また、 $\alpha$ が臨界値 $\alpha_c$ に近いインスタンスは解くことが難しいことが実験的に知られています。このように、ある臨界値を境に問題の性質が急激に変化する現象は相転移と呼ばれています。

このような背景から、K-SAT について、次の問題の解明が求められています。

• $\alpha \approx \alpha_c$ で問題が難しくなるのはなぜか？なぜ相転移が起こるのか？
• $\alpha \approx \alpha_c$ のインスタンスを高速に解くことのできるアルゴリズムを作ることはできるか？

本論文では、両方の問について考察します。

スピングラス理論

まず、スピングラス模型の基礎である Ising 模型について説明をします。Ising 模型は、 $N$ 個のスピン $s_1, s_2, \dots, s_N$ ($s_i$ は $\pm 1$ の2値を取る変数) からなる系であり、ハミルトニアンは次式で定義されます。

$$ E(\{s_i\}) = \sum_{i,j} J_{i,j} s_i s_j $$

$J_{i,j}$ は結合定数と呼ばれ、スピン $s_i$ と $s_j$ の間の相互作用を表します。 $J_{i,j}<0$ のときは $s_i,s_j$ が同じ向きを向くのが、 $J_{i,j}>0$ のときは $s_i,s_j$ が異なる向きを向くのがそれぞれエネルギーが小さくなり、安定になります。

$J_{i,j} = (\text{負の定数})$ とした最も基本的な模型は、磁石などの強磁性体のモデルとして用いられます。このモデルでは、各スピンの向きが揃うのが安定な状態であり、これは磁石の性質を捉えています。

スピングラス模型は、結合定数 $J_{i,j}$ の符号や大きさが結合によってランダムな値を取るモデルです。このモデルでは、どのようにスピンの値を決めても、 $J_{i,j}s_is_j>0$ となる不安定な結合が生じます。この不安定さはフラストレーションと呼ばれ、これによりスピングラス模型は複雑な挙動を示します。スピングラス模型のエネルギーは、下図に示すように多数の極小値を取ります。それぞれの谷は「状態 (state)」と呼ばれ、これらは非常に大きなエネルギーの壁で遮られています。

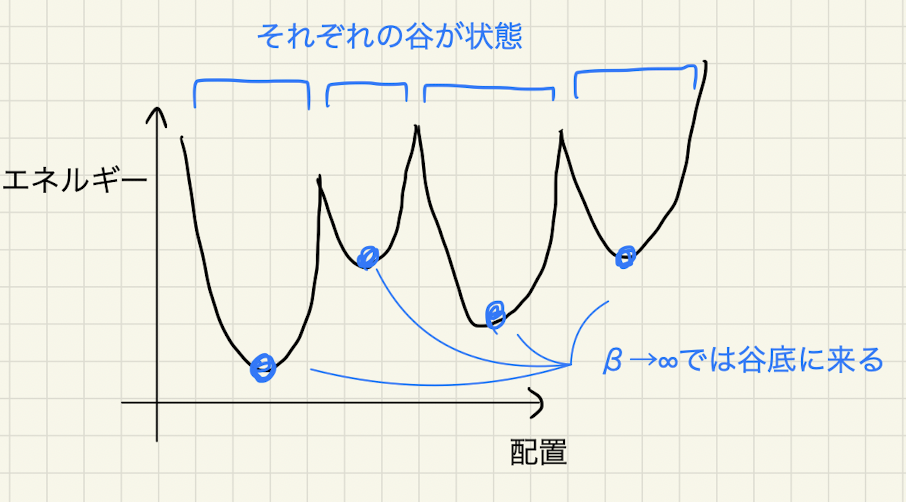
スピングラス模型を分析する手法は統計物理学において大きく発展しています。また、ニューラルネットワークや組合せ最適化問題など、情報科学における複雑な対象をスピングラス模型でモデル化し、解析する試みが多く行われています。

本論文では、K-SAT をスピングラス模型で表し、物理学において発展した手法である cavity 法を用いて K-SAT の挙動を分析します。

手法

スピングラス模型への帰着

K-SAT を以下のようにスピングラス模型に対応させます (前節でのスピングラス模型の説明では、ハミルトニアンは2つのスピンの積の和として定義されましたが、以下の対応では $K$ 個のスピンの積の和として定義されることに注意してください)。

• 変数 $x_i$ → スピン $s_i$:
  • $s_i=\begin{cases}1 & (x_i = \mathrm{true})\\ -1 & (x_i=\mathrm{false})\end{cases}$
• リテラル → 結合定数 $J$:
  • $J_a^r=\begin{cases}1 & (\text{節 $a$ の $r$ 番目のリテラルが肯定}) \\ -1 & (\text{節 $a$ の $r$ 番目のリテラルが否定})\end{cases}$
• 節のエネルギー: $\varepsilon_{J_a}(s_{i_1(a)},\dots,s_{i_K(a)}) = \begin{cases}0 & (\text{節 $a$ が $\mathrm{true}$}) \\ 1 & (\text{節 $a$ が $\mathrm{false}$})\end{cases}=2^{-K}\prod_{r=1}^K(1-J_a^r s_{i_r(a)})$
• 全エネルギー: $E = \sum_a \varepsilon_{J_a}$

すなわち、全エネルギーは充足されていない節の数です。インスタンスが充足可能であることと、全エネルギーの最小値 (基底エネルギー) が $0$ であることは同値です。

逆温度 $\beta \to \infty$ とした極限において、系はエネルギーの極小値を取ることが統計力学から導出されます。

スピングラス模型では、極小値が非常に多くあるため、 $\beta\to\infty$ の極限でも系の状態は定まりません。そこで、「極小値たちからなる系」の統計力学である “zero-temperature thermodynamics” を導入します。この系は、以下の式で支配されます。

$$ \exp(-Ny\Phi(y))=\int de \exp(N(\Sigma(e)-ye)) $$

• $\Phi(y)$: 「自由エネルギー」(通常の意味での自由エネルギーではないので、鉤括弧に入れている)
• $y$:「逆温度」(同上)
• $e$: エネルギー
• $\Sigma(e)$: “complexity”、エネルギー $e$ を持つ状態の個数の対数 (通常の統計力学におけるエントロピーに対応)

通常の熱力学において $\beta\to\infty$ の極限で系がエネルギーの極小値をとるのと同様に、$y\to\infty$ の極限で系の基底エネルギーが得られます。

Cavity 法の適用

Cavity 法は、「系の一部を取り出し、それと残りの系の関係を調べる」という考え方に基づく計算手法です。「残りの系」の振る舞いを詳細に記述するのは難しいので、代わりに系の平均値で置き換えるという近似を行います。

ここでは、節 $a$ を取り出して、それに含まれるスピン $s_i$ と、残りの系の関係を調べます。そのために、以下の2つの量を考えます。

• Cavity field $h_{i\to a}$
  • 「スピン $s_i$ が節 $a$ でどちらの向きを向きたいか」を表す量
  • すなわち、「節 $a$ を取り除いたときに、 $s_i$ がどちらの向きを向く傾向があるか」を表す量
  • 例えば、節 $a$ を取り除いた系において、 $s_i = 1$ となることが多いなら、節 $a$ でも $s_i$ は肯定リテラルであることが望ましいので、 $h_{i \to a} > 0$ となる。
• Cavity bias $u_{a \to i}$
  • 「節 $a$ が $\mathrm{true}$ となるために、スピン $s_i$ にどちらの向きを向いてほしいか」を表す量
  • 例えば、節 $a$ において $s_i$ が肯定リテラルなら、 $s_i=1$ となることが望ましいので、 $u_{a \to i}>0$ となる。

このように、cavity 法において、系は関数 (節) と変数 (スピン) の間の「メッセージ」のやり取りとして捉えられます。cavity field がスピンから節へのメッセージ、cavity bias が節からスピンへのメッセージに当たります。このような関数と変数の関係は、以下に示すような二部グラフで表現することができます。下図において、□ で表される頂点は関数 (節) で、○ で表される頂点は変数 (スピン) です。このグラフを因子グラフと呼びます。3-SAT の因子グラフでは、□ は 3 つの ○ とつながっており、○ は平均 $\alpha=M/N$ 個の □ とつながっています。

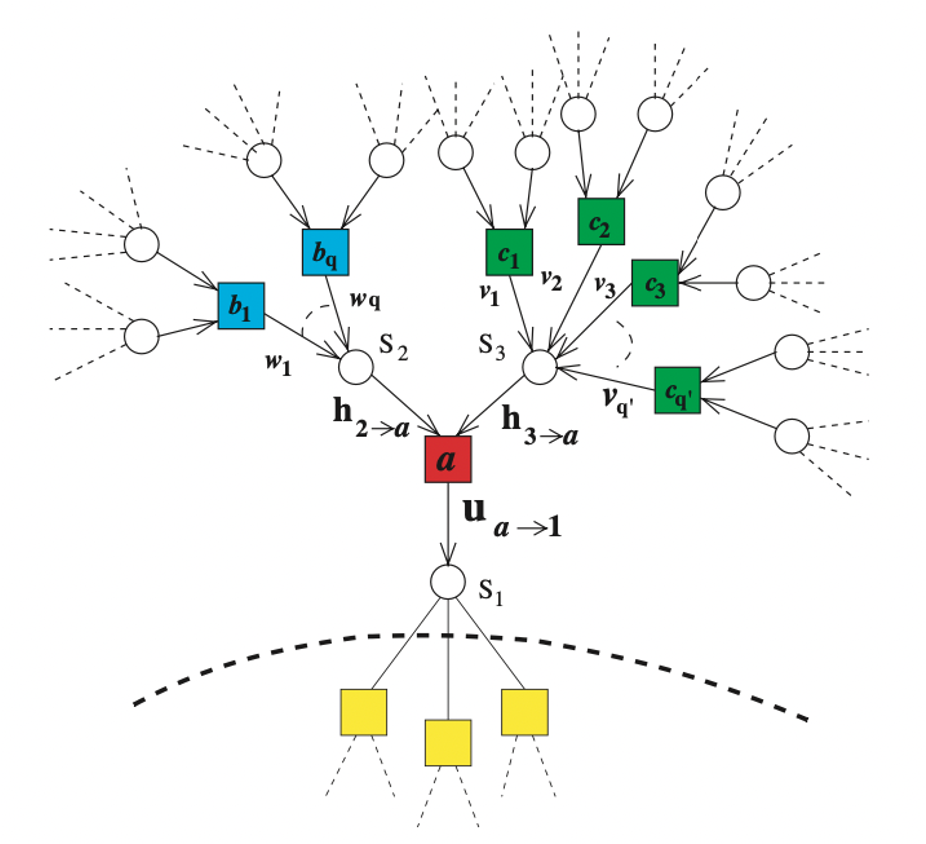
Cavity field と cavity bias の計算方法を説明します。まず、cavity field $h_{i \to a}$ については、節 $a$ 以外からの cavity bias の総和として求められます。

$$ h_{i \to a} = \sum_{b \neq a} u_{b\to i} $$

次に、cavity bias $u_{a \to i}$ については、節 $a$ について $s_i$ 以外のスピンを動かして全エネルギーを最小化したときの $s_i$ の係数として定義されます。このとき、 $s_i$ 以外の変数は、残りの系からの平均的な影響を cavity field を通して受けていると考えます。

$$ \min_{s_1,\dots, s_{i-1},s_{i+1},\dots, s_K} \left( \varepsilon_{J_a}(s_1,\dots,s_K) – \frac{1}{2} \sum_{j \neq i} h_{j \to a} s_j \right) = \frac{1}{2} \left( a_J( s_1,\dots, s_{i-1},s_{i+1},\dots, s_K) + s_i u_{a \to i}(h_1,\dots, h_{i-1},h_{i+1},\dots, h_K) \right) $$

すなわち、左辺を最小化した結果が右辺の形で表されるように $a_J, u_{a \to i}$ を定めます。ここで、 $a_J$ は節 $a$ の平均エネルギーです。 $a_J, u_{a \to i}$ は、 $\varepsilon_{J_a}$ の定義式を代入することで具体的に書き下すことができますが、ここでは省略します。

以上のように、 $h_{i \to a}, u_{a \to i}$ はお互いに定義し合う形になっています。これを連立方程式として解くことで、 $h,u$ の値が求められます。この連立方程式を解析的に解くのは困難ですが、確率伝搬法を用いて近似的に解くことができます。因子グラフが木ならば確率伝搬法は厳密解に収束することが示されています。K-SAT の因子グラフは木ではありませんが、疎グラフなので局所的に木と見なすことができ、局所的には正しい値が求められていると考えられます。

Cavity bias を重ね合わせた “survey” の導入

Cavity bias と cavity field は、状態 (局所最適解) ごとに定義される量です。複数の状態の扱い方には、いくつかの考え方があります。

最も簡単な方法は、単一の状態のみ考える方法です。これは RS (Replica Symmetry) 仮定と呼ばれます。計算は簡単になりますが、実際には多数の状態がある系を単一の状態によって代表させる近似は粗すぎるため、現実と整合しないことがあります。K-SAT の問題においては、RS 仮定に基づく計算は問題の性質を捉えきれません。

より正確な近似方法として、複数の状態を考え、それらを対等に扱うという方法があります。これは 1 step RSB (Replica Symmetry Breaking) 仮定と呼ばれます。これは、cavity bias の代わりに、 cavity bias の分布を考えることに対応します。Cavity bias の分布を survey $Q^{(y)}(u)$ と呼び、次の式で定義します。

$$ Q^{(y)}(u)=\sum_\omega \delta (u-u^{(w)}) $$

ここで、 $u^{(\omega)}$ は状態 $\omega$ の cavity bias です。また、和は $y$ によって選択される状態 $\omega$ について取ります。すなわち、zero-temperature thermodynamics において、「逆温度」が $y$ であるときに「自由エネルギー」 $\Phi$ を最小化するエネルギー、すなわち $\Sigma(e)-ye$ を最大化するエネルギー $e$ を持つ状態 $\omega$ について和を取ります。

Cavity bias の更新式に倣って、survey の更新式を導出すると以下のようになります。

$$ Q_{a\to 1}^{(y)}(u)=C \int \prod_{r=1}^q dw_r Q_{b_r \to 2}^{(y)}(w_r) \int \prod_{s=1}^{q’} dv_s Q_{c_s \to 3}^{(y)}(v_s) \delta(u-u_J(W,V)) \exp(ya_J(W,V)) $$

この式は、このままでは計算が困難ですが、 $\beta \to \infty$ の極限において単純化することができます。 $\beta \to \infty$ で、cavity bias $u_{a\to i}$ は $0, \pm 1$ の 2 値を取ります ($\pm 1$ のどちらかは、節 $a$ において変数 $i$ が肯定リテラルか否定リテラルかによります)。よって、survey は「cavity bias が $0$ となる状態の割合」という一つの実数で特徴づけられます。この事実を利用すると、より単純な survey の更新式が得られます。具体的な式については文献 [2] を参照してください。

平均インスタンスの挙動の解析

方法

ここでは、前節で説明した問題設定のもと、ランダムな K-SAT インスタンスの平均的な挙動を分析します。具体的には、以下の点に興味があります。

• $\alpha=M/N$ の値を変化させたときの、平均インスタンスの充足可能性
• 充足可能なら、解の発見の難しさ
• 相転移点 (問題の性質に急激な変化が起こる $\alpha$ の値)

まず、survey の更新式のインスタンス平均を取ります。次に、モンテカルロ法で survey を計算します。得られた survey から、自由エネルギー $\Phi(y)$ を $y$ の関数として求めます。自由エネルギー、エネルギー、complexity は Legendre 変換によって相互に変換可能であることが熱力学から導出されるため、求めた自由エネルギー $\Phi(y)$ から基底エネルギーと complexity を計算することができます。

結果

$\alpha$ を変えたときの、エネルギー $0$ の状態の complexity $\Sigma(0)$、基底エネルギー $e_0$、状態数が最大となるエネルギー $e_{th}$ の計算結果をグラフに表したものを下図に示します。今回は物理的な対象を扱っているわけではないので、縦軸に単位はありません。

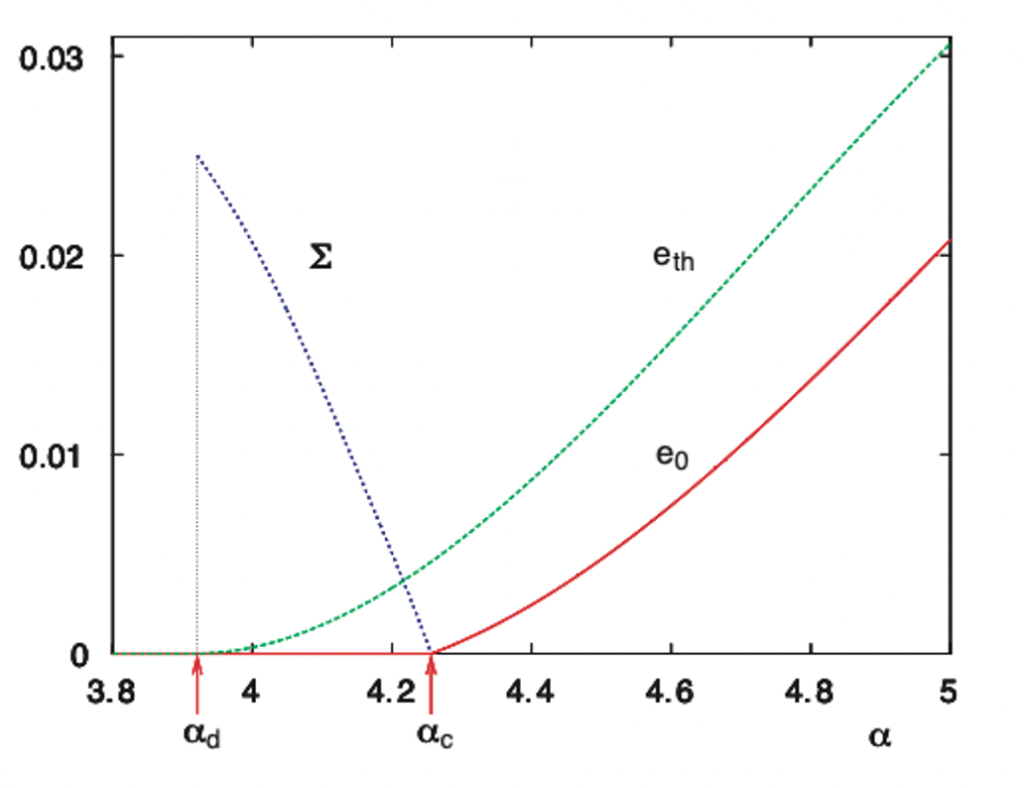
この図から、3 つの相の存在が確認できます。以下、それぞれの相の特徴について説明します。

1. SAT 相 $\alpha < \alpha_d \approx 3.9$
   • この相では、 $e_0 = 0$ であり、平均インスタンスは充足可能です。
   • この相では、すべての survey が $0$ となります。つまり、すべての状態で cavity bias が $0$ となります。これは、各スピンは特定の向きを向こうとしないことを意味し、一部のスピンをランダムに向き付けても、残りのスピンを適当に向き付けることで多くの場合に充足可能となります。
   • この相では、シンプルな山登り法や SA (Simulated Annealing) を用いて容易に解が求まります。
2. Hard-SAT 相 $\alpha_d < \alpha < \alpha_c \approx 4.3$
   • この相でも $e_0 = 0$ であり、平均インスタンスは依然として充足可能です。
   • この相では、 survey は $0$ 以外の値も取るようになります。また、 $\Sigma(0)$ が小さくなり、代わりに正のエネルギーを持つ状態が多くなります。これは、エネルギーが正の局所最適解が、エネルギー $0$ の解に比べて多数あることを意味します。そのため、SA などの探索アルゴリズムが局所最適解に陥り、エネルギーが $0$ の解に到達することが難しくなります。
3. UNSAT 相 $\alpha > \alpha_c$
   • この相では、 $e_0 > 0$ であり、平均インスタンスは充足不可能です。

経験的に知られている SAT-UNSAT 境界と一致する $\alpha_c$ が得られました。また、 $\alpha \approx \alpha_c$ で問題を解くことが難しくなるという現象に対して、「論理式を充足しない局所最適解が非常に多くなるから難しくなる」という説明を与えることに成功しました。

特定インスタンスに対するアルゴリズム

Survey propagation algorithm

ここでは、特定の K-SAT インスタンスが与えられたときに、効率的にインスタンスを解くアルゴリズムを考えます。

Cavity 法を用いて得られる各スピンの分布の情報を利用することで、次のようなアルゴリズムで解を構築することができます。

1. モンテカルロ法により survey を計算する
2. Survey から、cavity field の分布を計算する
3. Cavity field の分布から、スピンを決定する: $w_i^+, w_i^-$ をそれぞれ、スピン $s_i$ の cavity field が正/負になる確率とする。 $|w_i^+-w_i^-|$ が最大の $i$ を選んで、 $s_i$ を $w_i^+>w_i^-$ なら $1$、 $w_i^+<w_i^-$ なら $-1$ にする。
4. スピンが $1$ つ減った問題に対して、1-3 を繰り返す
5. Survey がすべて $0$ になったら、 SA で残りの問題を解く

手順 5 では、survey がすべて $0$ であるようなインスタンスは SAT 相にあるはずだから、簡単な SA で解けるという、前節で説明した結果を利用しています。

このアルゴリズムを survey propagation algorithm と命名します。

結果

Survey propagation algorithm を、 3-SAT の SAT-UNSAT 境界に近いインスタンスに適用して、解を見つけるまでの実行時間を計測し、既存のアルゴリズムと比較することで性能の評価を行います。

まず、既存のベンチマーク $\alpha \approx 4.2, N \approx 2000$ に対して survey propagation algorithm を実行しました。すべてのインスタンスに対して高速に解を見つけることができました。

次に、より大きなインスタンス $\alpha \approx 4.2, N \approx 10^5$ を複数作成し、 survey propagation algorithm を実行しました。これもすべてのインスタンスで、十分高速に解を見つけることができました。Survey propagation algorithm と同程度の性能を持つアルゴリズムは、高度にチューニングした walksat アルゴリズムのみでした。

時間計算量は、およそ $O(N^2)$ のオーダになることが観察されました。

結論

本論文では、cavity 法を用いて K-SAT 問題を解析し、以下のような結論が得られました。

平均インスタンスの挙動の分析:

• SAT-UNSAT 境界付近に Hard-SAT 相が存在することが確認された。
• Hard-SAT 相では、問題を充足しない局所最適解が非常に多く存在するため、単純な SA などの探索方法では解に到達することが難しいことが判明した。

特定インスタンスを解くアルゴリズムの構成:

• 与えられたインスタンスに対して cavity 法を適用して、各変数の値の分布が得られる。この情報を利用して変数の値を逐次的に決定する survey propagation algorithm を考案した。
• Survey propagation algorithm は、SAT-UNSAT 境界に近い大きなインスタンスに対しても効率的に解を発見することができた。これは、既存のほとんどのアルゴリズム (具体的には、高度にチューニングした walksat アルゴリズム以外) を上回る性能である。

あとがき

NP 完全問題のような非常に複雑な組合せ最適化問題に対しても、スピングラス理論の知見を適用することでアプローチできることが非常に興味深かったです。他の NP 完全問題に対しても、「局所最適解が増えることが難しさの原因である」という描像が得られるのか、逆に P 問題をスピングラス模型に帰着させたときにどのような挙動を示すのかに興味を持ちました。

参考文献

[1] M. Mézard, G. Parisi, R. Zecchina, “Analytic and Algorithmic Solution of Random Satisfiability Ptroblems,” Science, Vol 297, Issue 5582, pp. 812-815, 2002

[2] M. Mézard and R. Zecchina, “The random K-satisfiability problem: from an analytic solution to an efficient algorithm,” Phys. Rev. E 66 (2002) 056126