文献情報
タイトル :Fair Sampling Error Analysis on NISQ Devices
著者 :John Golden, Andreas Bärtschi, Daniel O’Malley, Stephan Eidenbenz
書誌情報 :https://doi.org/10.1145/3510857
概要
量子交互演算子アンザッツ(Quantum Alternating Operator Ansatz:QAOA)は最適化問題に対して有効で、Grover Mixier QAOAと呼ばれる手法は理論的に、全ての要素を等確率でサンプリングすること(フェアサンプリング)が可能です。しかし、実際のデバイスはノイズあり中規模量子(Noisy Intermediate Scale Quantum:NISQ)デバイスと呼ばれ、ノイズが存在しており、完全なフェアサンプリングは難しいです。
本論文ではNISQデバイスにおけるGrover Mixier QAOAのフェアサンプリングの現状について調査します。
背景・課題
量子アニーリングは組合せ最適化問題に対するヒューリスティックとして提案されました。しかし、量子アニーリングに対する直接的な手法では最適解が複数存在した場合、フェアサンプリングすることが不可能であることが実験的に証明されました。量子アニーリングのフェアサンプリング性を向上させる手法として、より複雑なハミルトニアンを導入する手法が提案されていますがシステム的な偏り(バイアス)が残ってしまう場合もあります。
量子交互演算子アンザッツ(Quantum Alternating Operator Ansatz:OAOA)も量子アニーリングと同様に最適化問題に対して有効であるヒューリスティックな量子アルゴリズムです。中でもGrover Mixier QAOAと呼ばれる手法は、ノイズのない理想的なデバイスにおけるフェアサンプリング性を理論的に保証します。しかしながら、現在のゲート型の量子コンピュータはノイズあり中規模量子(Noisy Intermediate Scale Quantum:NISQ)デバイスと呼ばれ、ノイズが存在しています。本論文では現在のNISQデバイスのGrover Mixier QAOAについて、ノイズが量子ビットのfidelity(精度)と基底状態間のフェアサンプリングの両方に与える影響を分析します。
以下は本文で用いられる用語です。
フェアサンプリング
サンプリングとは母集団から一部の要素を抽出することを指します。フェアサンプリングとはサンプリングの際、全ての選択可能な要素を等確率でサンプリングすることを指します。これにより最適解を偏りなく探索することが可能となります。逆にフェアサンプリングが行われない場合、全ての最適解を探索することが不可能となる場合が考えられます。
量子交互演算子アンザッツ(QAOA)
QAOAはゲート方式の量子コンピュータ上でユニタリ演算子US(問題インスタンスの全ての解の重ね合わせを生成) に対しユニタリ演算子 UP(γk)と混合ユニタリ演算子 UM(βk) を交互にp 回を適用し、最終的に計算基底での測定を行うことで実行されます。具体的なQAOAの手順については最後の「付録」に示します。
量子ボリューム(Quantum Volume : QV)
量子ボリューム(Quantum Volume : QV)とは、NISQデバイスの性能を評価する指標であり、システムのエラーが少ないほど高い数値を示します。
実験方法
本実験ではIBM Qシステム(IBM社が提供する量子コンピュータサービス)をqiskit(IBM社が提供する量子コンピュータ向けのフレームワークでIBM Qを操作可能)を用いて実行します。以下に示すテスト問題を解くための量子回路を作成し、各量子回路ごとに40,960回のショットを収集しました。集めたデータからNISQデバイスにおけるフェアサンプリング性と量子ビットのfidelityの関係、さらにはaggregate errorとフェアサンプリング性を比較することによってNISQデバイスのフェアサンプリング性を検証します。
テスト回路
図1は最適解が複数存在する問題の一覧です。左から問題番号、イジング模型$H_C=-\sum J_{ij}Z_iZ_j$、イジング模型のハミルトニアン、$q0=↑$とした場合の基底状態を示しています。濃い赤色、薄い赤色のエッジは強磁性結合$J_{ij}=+2,J_{ij}=+1$を、濃い青色、薄い青色のエッジは反強磁性結合$J_{ij}=-2,J_{ij}=-1$を表しています。なお、$n$量子ビットの問題は$q0$を$↑$に固定することで$n-1$量子ビットの問題として扱うことができ、例えば(a)問題は4L,4T,5T回路で解くことができます。図3は図2の問題を実デバイスに反映させる際の、ハードウェアの構造の候補を表しています。
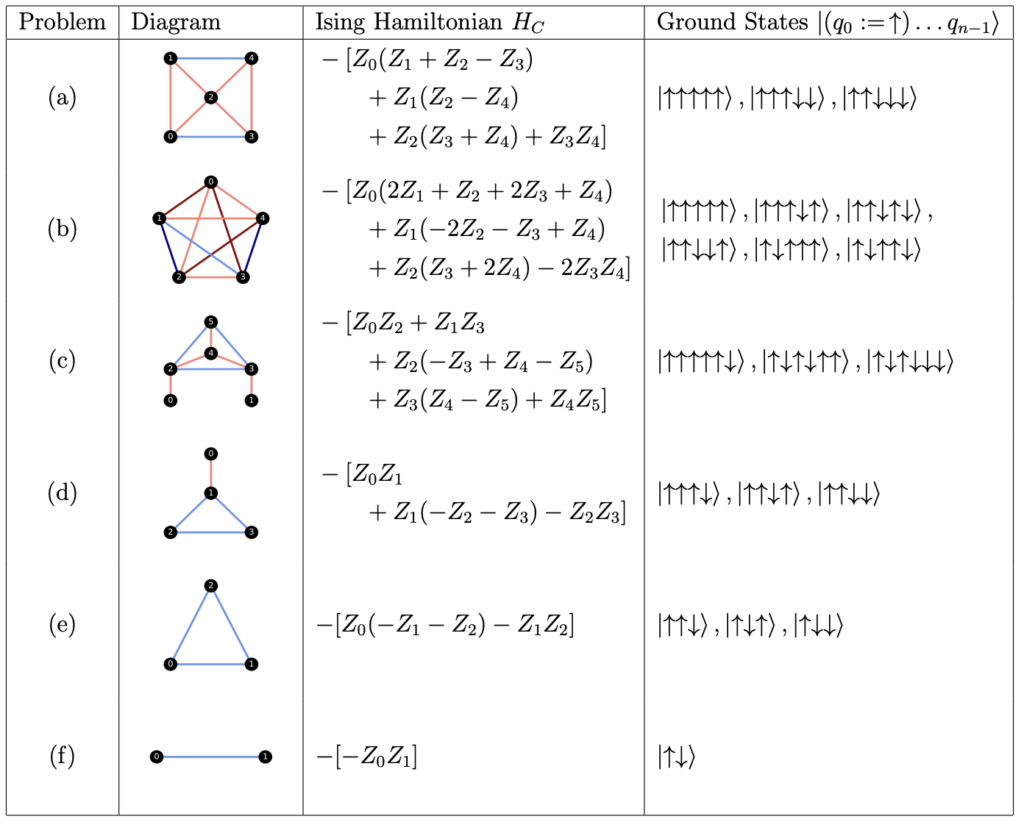
図1:NISQハードウェアでテストする縮退した基底状態を持つイジング模型

図2:テスト問題を埋め込むNISQハードウェアの構造
Number of Shots to Reject Fair Sampling : NSRFS
NSRFSはピアソンのカイ二乗検定を用いた量子回路のフェアサンプリング性を示す指標です。ピアソンのカイ二乗検定とは、帰無仮説と呼ばれる仮説とそれに対する対立仮説を設定し、ピアソンのカイ二乗検定統計量(式(1))はカイ二乗分布と呼ばれる確率分布に従うと仮定して行う統計的検定です。統計量と確率分布の差異が有意水準:$α$以下であれば帰無仮説を採択します。一方で、有意水準以上であれば帰無仮説を棄却し対立仮説を採択します。式(1)中の期待値Eと実測値$O$は帰無仮説の下における値です。
$$
\chi^2 = \sum_{i} \frac{ \left( O_{i} – E \right)^2 }{E}
\tag{1}
$$
今回、帰無仮説を「量子回路は完全なフェアサンプリング性を示す」と設定しました。一方で対立仮説は「量子回路は完全なフェアサンプリング性を示さない」と設定しました。この時、帰無仮説の下における期待値$E$は、回路の縮退した基底状態の数$d$、観測された基底状態数$n_{g.s.}$を用いて式(2)で表されます。
$$
E_{i} = E = \frac{n_{g.s.}}{d}
\tag{2}
$$
aggregate error
aggregate errorは特定のハードウェア上で与えられた回路の精度を表す指標として有効であると考えられます。IBM Qをqiskitで実行する際、qiskitは個々の量子ビットの測定誤差とネイティブゲートセット(CX, SX, RX, RZ)の誤差率を報告します。これを用いて、量子ビット$q_1,…q_l$に作用するゲート$g_1,…,g_k$を持つ回路Cについて、チップ$H$上で評価される場合そのaggregate error$E_{CH}$を式(3)で定義します。
$$
E_{C,H} = 1- \left(\prod_{i=1}^k \left(1-e_i \right) \right) \left(\prod_{i=1}^l \left(1-m_i \right) \right)
\tag{3}
$$
$e_i、m_i$はそれぞれqiskitによって報告されたゲート$g_i$のエラー率、量子ビット$q_i$の測定誤差です。
結果
基底状態確率とフェアサンプリング性
図3はテスト問題(d)(e)(f)における基底状態確率とNSRFSの関係を示しています。その結果、この二つには正の相関関係があることが確認されました。このような関係を「ソフトアンフェア」であるとし、ソフトアンフェアな回路では基底状態確率の向上と公平なフェアサンプリング性は高性能な量子ビットを用いることで実現されます。
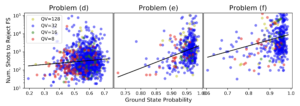
図3:(d),(e),(f)問題に対する回路の基底状態確率とNSRFS
黒線:回帰直線
図4はテスト問題(a)(b)(c)における基底状態確率とNSRFSの関係を示しています。(a)問題に対する4T回路はソフトアンフェアな性質を示し、4L回路は基底状態確率とNSRFSの間に相関を示しませんでした。しかし、5T回路ではその二つの間に負の相関関係が確認されました。これは高い基底状態確率と高いフェアサンプリング性を同時に実現できないことを示しており、(b),(c)問題に対する回路でも同様の結果となりました。このような関係を「ハードアンフェア」であるとします。
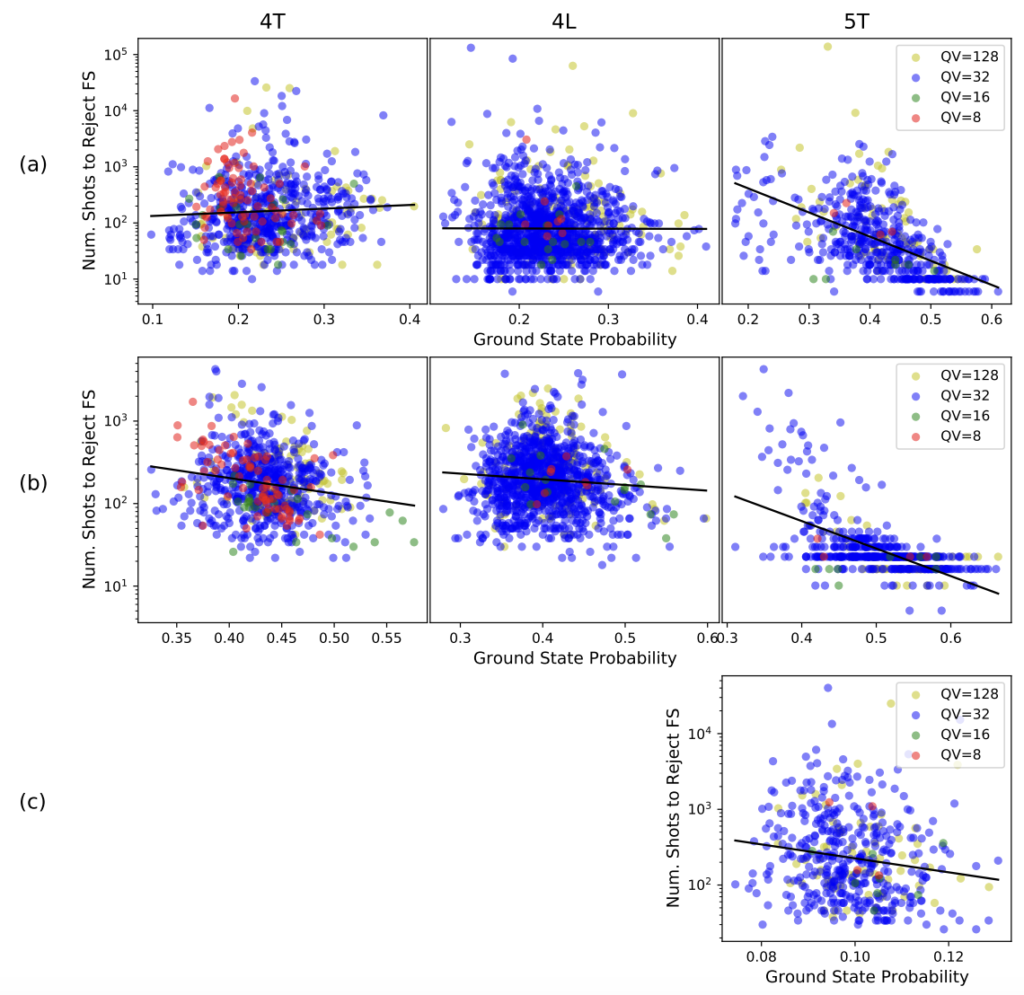
図4:(a),(b),(c)問題に対する回路の基底状態確率とNSRFS
黒線:回帰直線
aggregate errorとフェアサンプリング性
図5はハードアンフェア回路(回路(b))とソフトアンフェア回路(回路(e))におけるaggregate errorと基底状態確率(図6左)、NSRFS(図6右)の関係を示したものです。図6左に示す結果から、いずれの回路においてもaggregate errorの増加とともに基底状態確率の低下が確認されました。図5右に示す結果について、問題(e)に対する回路ではaggregate errorの増加とともにフェアサンプリング性が低下していることが確認されました。一方、問題(b)に対する回路ではaggregate errorの増加とともにフェアサンプリング性が増加していることが確認されました。また、量子ボリューム(Quantum Volume : QV)とaggregate errorには弱い正の相関があることが確認されました。
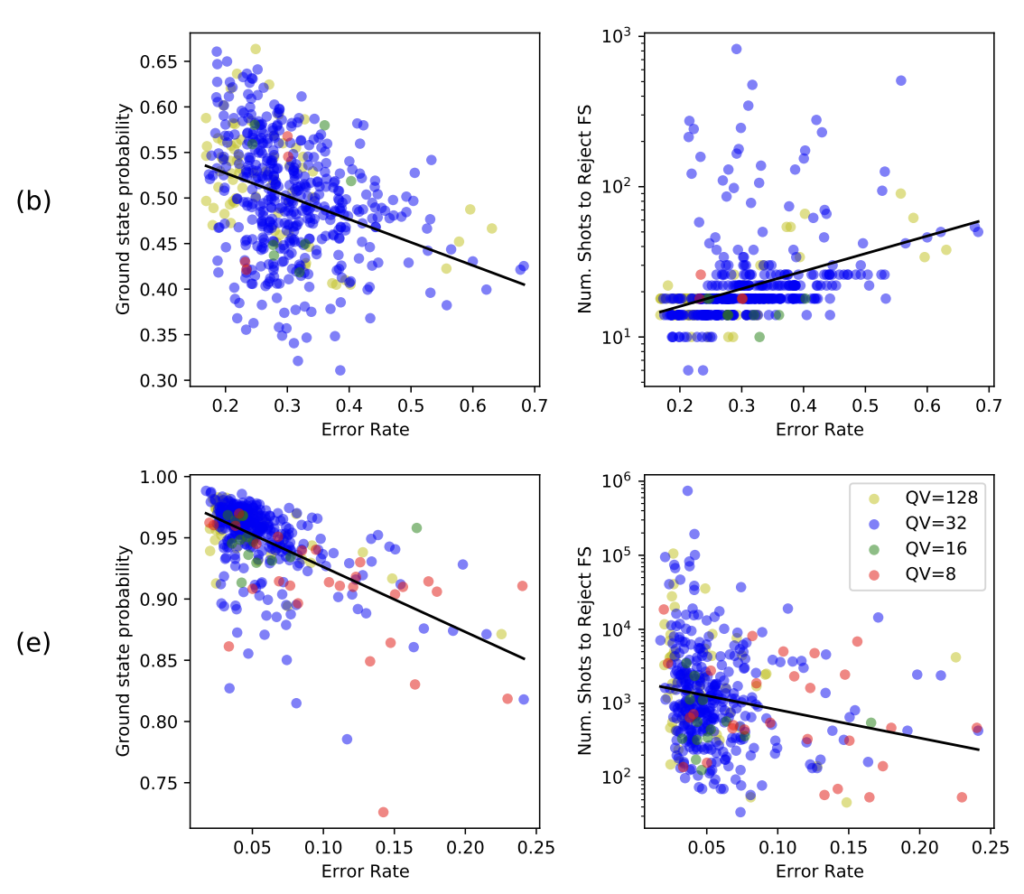
図5:問題(b),(e)に対する回路のaggregate errorと基底状態確率(左)、NSRFS(右)
黒線:回帰直線
図6はすべての回路におけるaggregate errorとNSRFSの関係を示したものです。この結果から、フェアサンプリング性はaggregate errorが最も小さい時に最も高く、またaggregate errorがおよそ0.5に近づくと低下し、その後再び上昇することが観察されます。
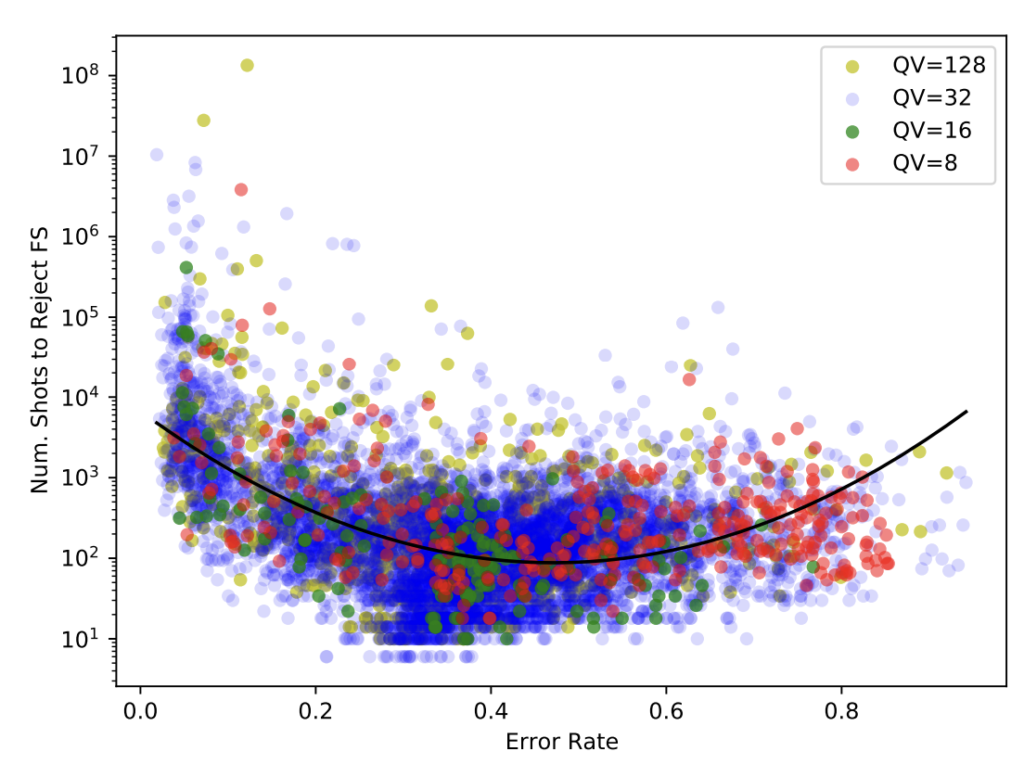
図6:すべての問題に対する回路のaggregate errorとNSRFS
黒線:近似曲線
考察
基底状態確率とフェアサンプリング性
ハードアンフェアの原因はノイズの多い量子ビットが大きな量子回路に組み込まれることにより、よりランダムなサンプリングを行うことによる可能性があります。これにより、基底状態確率は下がるものの、高いフェアサンプリング性が得られると考えられます。
aggregate errorとフェアサンプリング性
ソフトアンフェア回路についてaggregate errorとNSRFSに負の相関が見られたのは、aggregate errorの増加により、ある基底状態が他の基底状態よりも有利になるようなバイアスが生じてる可能性があります。図7に示す結果から、ハードウェアのバイアスがaggregate errorの指標の中央で支配的であることを示し、さらにデバイスのエラーが増加すると全体のバイアスは打ち消され、その結果フェアサンプリングが実現されていると考えられます。
結論
本研究ではNISQデバイスのフェアサンプリング性を評価するためにNSRFSと呼ばれる指標を定義しました。NISQデバイスのNSRFSには以下のような特徴が見られました。
- 3量子ビットで構成された回路では精度の高い量子ビットを用いることによって高いフェアサンプリング性を得ることができる(ソフトアンフェア)
- 4量子ビット以上で構成された回路では精度の高い量子ビットを用いても高いフェアサンプリング性を得ることができない(ハードアンフェア)
さらに、本論中で定義した回路の精度を評価するaggregate errorとNSRFSの間には線形の関係が見られませんでした。これらの結果から、NISQ回路のフェアサンプリング性には回路内部の偏りがお互いに打ち消しあい、全体としてフェアサンプリングが実現されていることがわかりました。
QAOAについて
付録
以下ではQAOAによって最適解が求められる理由を、周辺の知識も合わせて示します。
量子状態と重ね合わせの原理
量子状態は波動関数$\psi$によって表されます。ある量子状態$\psi$は別の量子状態$\psi_1, \psi_2, \cdots, \psi_n$の線型結合)で表すことができます。(重ね合わせの原理)
$$
\begin{align}
\psi = \sum_{i}^{n} c_{i} \psi_{i} = \sum_{i} a_{i} \quad(c_{i} \in C)
\end{align}
\tag{4}
$$
ブラケット記法
量子力学において量子状態を記述するための記法です。ある量子状態が複数の量子状態の線型結合で表される場合、その要素を列ベクトルの要素として並べたものがブラケット記法で表すものです。
次の式はケットベクトルと呼ばれるものです。量子状態を表すベクトルであることから状態ベクトルとも呼ばれます。
$$
\begin{align}
\label{ket}
\ket{\psi} = (a_0, a_1, \cdots, a_n)^\top
\end{align}
\tag{5}
$$
ケットベクトルの随伴行列(行列Aの各要素を複素共役な数をとり、さらに行列に転置を施したもの)はブラベクトルと呼ばれ、次の式で表されます。
$$
\begin{align}
\label{bra}
\bra{\psi} = \ket{\psi}^{\dagger} = (a_0^*, a_1^*, \cdots, a_n^*)
\end{align}
\tag{6}
$$
期待値
古典的な系の物理量$A$の期待値$\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}} \ev{A}$は、確率密度関数$P(x)$を用いて次の式で定義されます。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\begin{align}
\label{exp}
\ev{A} = \int_{-\infty}^{\infty} A P(x) dx
\end{align}
\tag{7}
$$
確率密度関数$P(x)$は以下の規格化条件を満たします。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\begin{align}
\label{norm}
\int_{-\infty}^{\infty} P(x) dx = 1
\end{align}
\tag{8}
$$
さらにある量子状態$\ket{\psi(x)}$の確率密度関数$P(x)$は次の式で表されます
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\begin{align}
\label{prob}
P(x) = \ket{\psi(x)}^* \ket{\psi(x)} = \braket{\psi(x)}{\psi(x)}
\end{align}
\tag{9}
$$
天下り的ではありますが、物理量$A$が量子的な系の場合の期待値$\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}\ev{A}$は、その演算子を$\hat{A}$とした時、次の式で表されます。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\begin{align}
\label{exp_q}
\ev{A}
&= \int_{-\infty}^{\infty} \hat{A} P(x) dx\\
&= \hat{A} \braket{\psi(x)}{\psi(x)}\\
\end{align}
\tag{10}
$$
ここで、演算子$\hat{A}$が$A$に対する固有値で、$\ket{\psi(x)}$がそれに対する固有ベクトルだとすると、固有ベクトルの定義より固有値と固有ベクトルの間には
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\begin{align}
\label{equ:eigen}
A \ket{\psi(x)} = \hat{A} \ket{\psi(x)}
\end{align}
\tag{11}
$$
が成立するので、量子的な物理量$A$の期待値$\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}\ev{A}$は次の式で表されます。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\def\evv#1#2{\mathinner{\left\langle{#2}|{#1}|{#2}\right\rangle}}
\begin{align}
\label{equ:braket-exp-2}
\begin{split}
\ev{A}
&= \hat{A} \braket{\psi(x)}{\psi(x)}\\
&= \evv{\hat{A}}{\psi(x)}\\
&= \evv{A}{\psi(x)}\\
\end{split}
\end{align}
tag{12}
$$
変分法
ハミルトニアン$H$はエルミート行列であるため、その固有値$\lambda$は実数である。ハミルトニアン$H$に対する固有値を$E$とし、それに対する固有ベクトルを$\ket{\psi}$とする。さらに、固有値の最小値を$E_0$とし、それに対する固有ベクトルを$\ket{\psi_0}$とします。このとき、固有値と固有ベクトルの関係から次の式が成り立ちます。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\def\evv#1#2{\mathinner{\left\langle{#2}|{#1}|{#2}\right\rangle}}
\begin{align}
\begin{split}
H\ket{\psi} &= E\ket{\psi}\\
H\ket{\psi_0} &= E_0\ket{\psi_0}
\end{split}
\end{align}
\tag{13}
$$
$E_0$は固有値の最小値であるため$E \ge E_0$です。よって任意の状態$\ket{\psi}$に対し、次の式が成り立ちます。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ev#1{\mathinner{\left\langle{#1}\right\rangle}}
\def\evv#1#2{\mathinner{\left\langle{#2}|{#1}|{#2}\right\rangle}}
\begin{align}
\evv{H}{\psi} \ge E_0
\end{align}
\tag{14}
$$
最適化問題に対するQAOA:Quantum Approximate Optimization Algorithm
以上で説明した内容を踏まえ、論文中でoriginal approachと紹介された手法について整理します。
- step1
組合せ最適化問題を定式化し目的関数$C(z)$を作成
$$
\begin{align}
\begin{split}
C(\bm{z}) &= \sum_{\alpha=1}^m C_{\alpha}(\bm{z})\\
\bm{z} &= (z_1, z_2, \cdots, z_n)
\end{split}
\end{align}
\tag{15}
$$ - step2
初期状態
$$
\begin{align}
\ket{\psi} = \frac{1}{\sqrt{2^n}} \sum_{\bm{z}} \ket{\bm{z}}
\end{align}
\tag{16}
$$
を作成 - step3
初期状態に作用するユニタリ演算子を以下のように定義する。
$$
\begin{align}
U(C,\gamma) = e^{-i\gamma C} = \prod_{\alpha=1}^m e^{-i\gamma C_{\alpha}}
\end{align}
\tag{17}
$$
$$
\begin{align}
\begin{split}
U(C,\beta) &= e^{-i\beta B} = \prod_{j=1}^n e^{-i\beta \sigma_j^x}\\
B &= \sum_{j=1}^n X_j
\end{split}
\end{align}
\tag{18}
$$
また、初期状態に対しそれぞれ$p$個の$U(C,\gamma)$と$U(C,\beta)$を適用したものを次の式で表します。
$$
\begin{align}
\begin{split}
\ket{\bm{\gamma}, \bm{\beta}} = U(B,\beta_p)U(C,\gamma_p) \cdots U(B,\beta_1)U(C,\gamma_1) \ket{\psi}
\end{split}
\end{align}
\tag{19}
$$
パラメータ$\beta, \gamma$に対して上式で定義した$\ket{\bm{\gamma}, \bm{\beta}}$を量子回路上で設計します。 - step4
$C(z)$の期待値$\def\evv#1#2{\mathinner{\left\langle{#2}|{#1}|{#2}\right\rangle}} \evv{C(z)}{\bm{\gamma}, \bm{\beta}}$を量子コンピュータを用いて計算し、古典コンピュータで$C(z)$の期待値が小さくなるようにパラメータ$\beta, \gamma$を更新します。 - step5
step2~step4を繰り返し、最適なパラメータ$\beta’, \gamma’$を得ます。得られた$\beta’, \gamma’$に対し$\ket{\bm{\gamma’}, \bm{\beta’}}$から$\bm{z}$を取得し、これが最適化問題の解となります。
あとがき
量子回路に触れる初めての機会で、読み進めるのに難航しましたが、量子アニーリングと量子ゲートの違いやフェアサンプリングの重要性、統計的検定など広く学ぶことができました。初読の段階ではフェアサンプリングが実現できるものだと思い込んでいました。読み進めてみると完璧には実現できないが、高性能な量子ビットを用いた場合と、逆に低性能な量子ビットを用いた場合に高いフェアサンプリング性を実現できるとの結論に至りました。この結論に混乱してしまいましたが、低性能な量子ビットが乱数生成機のように振る舞っていると飲み込むことで乗り越えました。
論文ではこのような結果になっているものの、図7からError Rateの小さい量子回路のフェアサンプリング性はError Rateの大きいそれと比べ、明らかに性能が良いように私は見て取れます。しかしながら、本文でも指摘されていた通り量子デバイスを評価する際にはQVだけではなく、複数の評価基準を用いて判断することが重要であるという点については納得しました。また、今回QVという指標が導入されましたが、この指標の有用性についても勉強したいと思いました。