文献情報

• タイトル：Constrained quantum annealing of graph coloring
• 著者：Kazue Kudo
• Doi リンク：https://doi.org/10.48550/arXiv.1806.05782

概要

量子アニーリングでは、組合せ最適化問題の制約は罰金項として表現することが一般的です。しかしこの手法は量子アニーリング (QA) の性能を落としてしまうことが知られています。本論文では 制約付き量子アニーリング (Constrained Quantum Annealing, CQA) と呼ばれる手法を用いて組合せ最適化問題を解きます。この手法は制約を罰金項として表現するのではなく、量子効果を表す driver Hamiltonian を適切に用いることで制約を満たした解のみに限定して探索を行うことができる手法です。本論文では組合せ最適化問題の一例としてグラフ彩色問題に注目して、グラフ彩色問題を CQA を用いて解きます。実験の結果では CQA により最適解に近い解を得ることができました。一方で予想と違う結果も得られ、この考察も行います。

背景・課題

イジング模型とグラフ彩色

量子アニーリングでは組合せ最適化問題のコスト関数をハミルトニアンとして表現します。ハミルトニアンはイジング変数 $\sigma_{i} ∈ \{−1,1\}$ と 2 つのイジング変数間の相互作用の係数 $J_{ij}$、局所磁場 $h_{i}$ を用いて以下の形 (1) 式で表されます。

$$
H(\sigma) = – \sum_{i<j} J_{ij}\sigma_{i}\sigma_{j} – \sum_{i} h_{i}\sigma_{i} \tag{1}
$$

本論文では組合せ最適化問題としてグラフ彩色問題に着目します。グラフ彩色問題とは辺で隣接した頂点に対して同じ色を割り当てないように各頂点を 1 色で彩色する問題のことです。図 1 にグラフ彩色問題の例を示しました。図 1(b) の例では隣接した頂点に同じ色を割り当てているのでグラフ彩色問題の解としては不適切です。

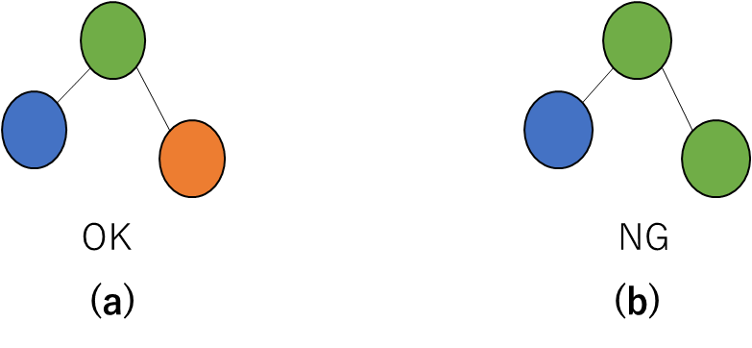
実際にグラフ彩色問題をイジング模型として定式化してみます。

グラフは頂点数を $n$、辺数を $m$ として、彩色に用いる色の数を $q$ とします。イジング変数は $\sigma_{i,a} \in \{-1,1\}$ とします。これは頂点 $i$ に色 $a$ を割り当てるとき $\sigma_{i,a} = 1$、それ以外で $\sigma_{i,a} = -1$ となります。

隣接した頂点に同じ色を割り当てないことを表す項は以下の (2) 式となります。ここで $E$ は辺の集合を表し、$(ij) \in E$ は頂点 $i$ と頂点 $j$ が隣接していることを表します。頂点 $i$ に色 $a$ が割り当てられるとき $\frac{\sigma_{i,a}+1}{2} =1$、それ以外で $\frac{\sigma_{i,a}+1}{2} =0$ となるので、頂点 $i$ と頂点 $j$ に同じ色 $a$ が割り当てられないとき $\frac{\sigma_{i,a}+1}{2}\frac{\sigma_{j,a}+1}{2}=0$ となり $H_{1}$ は最小値 0 をとります。

$$
H_{1} = \sum_{(ij) \in E} \sum_{a=1}^{q} \frac{\sigma_{i,a}+1}{2} \frac{\sigma_{j,a}+1}{2} \tag{2}
$$

ここからは各頂点に 1 色だけ割り当てる制約を定式化します。まず、各頂点に 1 色だけ割り当てるときは以下の (3) 式を満たします。これは $\sigma_{i,a}=1$ となる色 $a$ が１つだけあり、$\sigma_{i,a}=-1$ となる色 $a$ が $q − 1$ 色あるからです。

$$
\sum_{a=1}^{q} \sigma_{i,a} = 1 \cdot 1 + (-1) \cdot (q-1) = 2 – q \tag{3}
$$

このような制約はイジング模型として次の (4) 式のように定式化されます。$\sum_{a=1}^{q} \sigma_{i, a} = 2 -q$ を満たすとき $H_{2}$ は最小値 0 をとります。

$$
H_{2} = \sum_{i=1}^{n} \left( \sum_{a=1}^{q} \sigma_{i,a} – (2-q) \right)^{2} \tag{4}
$$

よってグラフ彩色問題をハミルトニアンとして定式化すると次の (5) 式で表すことができます。

$$
H = H_{1} + \alpha H_{2} \tag{5}
$$

このように制約をハミルトニアンとして定式化するためには二乗の項を加えるのが一般的です。このような項を罰金項と呼びます。しかし罰金項を用いる手法は量子アニーリングの性能を落としてしまうことが知られています。

量子モンテカルロ法

量子アニーリングを古典コンピュータ上でシミュレーションする手法に量子モンテカルロ法があります。この手法では実は、制約を満たした中で解を探索できるので罰金項を用いる必要がありません。

量子モンテカルロ法では複数のハミルトニアンとそれらの相互作用を用いて解を探索します。以下に量子モンテカルロ法のアルゴリズムの概要を示しました。

1. 1 つのハミルトニアンに対して解の状態を少しだけ変化させる
2. 変化する前後のハミルトニアンの値を計算し、実際に解を遷移させるか決定する
3. 上記をすべてのハミルトニアンに対して繰り返す

このアルゴリズムのグラフ彩色問題における例を図 2 に示しました。このアルゴリズムでは解の状態を変化させるとき、変化させた後の状態が制約を満たした解になっていれば常に制約を満たした解を探索することができます。例えば図 2 では解を変化させるときに 1 つの頂点の色を変更していますが、この変更方法は頂点に 1 色だけ割り当てる制約を常に満たすことができます。

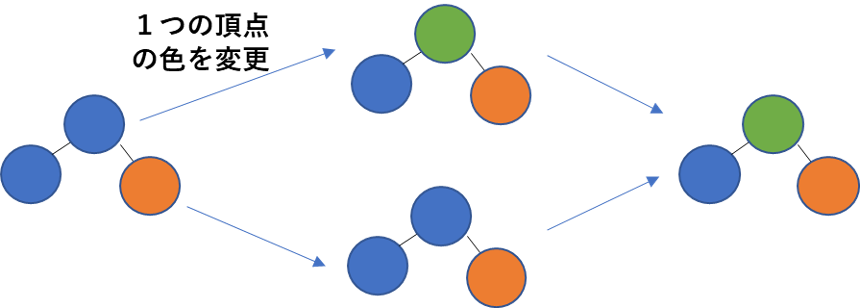
一方で量子モンテカルロ法は縮退 (同じエネルギー値を持つ状態が複数あること) が起きる問題に対しては非効率的になることが知られています ([1])。グラフ彩色問題で縮退が起きている状態を図 3 に示しました。これらはすべて異なる状態ですが、エネルギー値は等しくなります。

実はグラフ彩色問題は縮退度が高い問題です。なぜなら、グラフが $q$ 色で彩色可能 ($q$ 色のグラフ彩色問題の解が存在する) な時にはグラフ彩色問題の解の個数は少なくとも $q!$ 通りあるからです。例えば図 3 の例では 3 色割り当てる方法が $3! = 6$ 通り存在します。また図 3 の例のように頂点数 $n$ と $q$ が等しいときに色の割り当て方は $q!$ 通りになります。

量子モンテカルロ法がグラフ彩色問題のような縮退度が高い問題に対して非効率的になる例を図 4 に示しました。図 4 では初期状態からハミルトニアンの値を減少させるのに 3 回色の変更を行う必要がありましたが、頂点数が多いグラフでは色の変更回数がさらに増えてしまい非効率的となります。

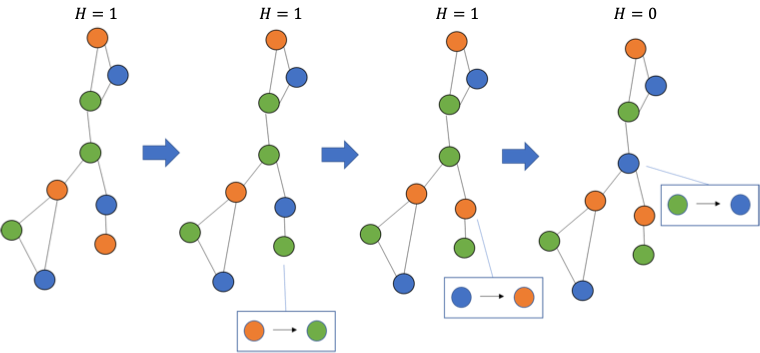
量子モンテカルロ法が縮退度の高い問題に対して非効率になる一方で、縮退度の高い問題は量子アニーリングにおいては有利になります。これは基底状態 (エネルギーが最小になる状態) の数が多くなり、基底状態に到達しやすくなるからです。

量子アニーリングにおけるハミルトニアン

これまでは古典的なハミルトニアンを考えていました。ここでは量子アニーリングにおけるハミルトニアンを考えます。量子アニーリングにおけるハミルトニアンは次の (6) 式で表されます。

$$
H = sH_{p} + (1 – s)H_{d} \tag{6}
$$

$s$ は時間に依存するパラメータです。$0 \leq t \leq T$ の間で量子アニーリングを行うときパラメータ $s$ は $s(0) = 0$、$s(T)=1$ を満たします。

$H_{p}$ は problem Hamiltonian と呼ばれる項です。この項は組合せ最適化問題のコスト関数を表し、古典的なハミルトニアンにおけるイジング変数 $\sigma_{i}^{z}$ をパウリ行列の z 成分 $\hat{\sigma}_{i}^{z}$ に置き換えることで得られます。パウリ行列の z 成分を次の (7) 式に示しました。

$$
\hat{\sigma}_{i}^{z} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \tag{7}
$$

$H_{d}$ は driver Hamiltonian と呼ばれる項です。この項は量子効果を表しています。例として横磁場イジング模型の driver Hamiltonian を次の (8) 式に示しました。

$$
H_{d} = \sum_{i=1}^{N} \hat{\sigma}_{i}^{x} \tag{8}
$$

ここで $\hat{\sigma}_{i}^{x}$ はパウリ行列の $x$ 成分で、これを次の (9) 式に示しました。

$$
\hat{\sigma}_{i}^{x} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \tag{9}
$$

$\hat{\sigma}_{i}^{x}$ はスピンの向きを反転させる性質があります。上向きと下向きのスピンをそれぞれ $\ket{\uparrow} = (1, 0)^T, \ket{\downarrow}=(0, 1)^T$ と書くことにします。ここで $\ket{\cdot}$ はケットと呼ばれ、列ベクトルで表される量子状態を指しています。このとき　$\hat{\sigma}_{i}^{x} \ket{\uparrow}_i = \ket{\downarrow}_i$、$\hat{\sigma}_{i}^{x} \ket{\downarrow}_i = \ket{\uparrow}_i$ となります。

このように driver Hamiltonian は上向きと下向きを入れ替えながら解を探索します。

量子アニーリングは $0 \leq t \leq T$ において $s(0)=0, s(T)=1$ を満たすので $H(0)=H_{d}, H(T)=H_{p}$ となります。つまり解の初期状態は $H_{d}$ の基底状態ですが、$t=T$ では解は $H_{p}$ の基底状態となり最適化問題の解を得ることができます。

状態が時間に対してどのように変化するかはシュレディンガー方程式によって表されます。シュレディンガー方程式を次の (10) 式に示しました。

$$
i \frac{\partial}{\partial t} \ket {\psi(t)} = H(t) \ket{\psi(t)} \tag{10}
$$

ここで $\ket{\psi(t)}$ は系の状態で、$H(t)$ はハミルトニアンです。

手法

本論文では 制約付き量子アニーリング (Constrained Quantum Annealing, CQA) [2] と呼ばれる手法を用います。これは量子アニーリングで制約を罰金項として加えずに driver Hamiltonian を工夫することで制約を満たした解に限定して探索を行うことができる手法です。

制約が次の (11) 式の形で表されているとします。$C$ は任意の制約で、$c$ は定数行列です。

$$
C(\{\hat{\sigma}_{i}^{z} \}) = c \tag{11}
$$
CQA で用いる driver Hamiltonian $H_{d}$ はこの制約 $C$ に対して次の (12) 式の条件を満たす必要があります。

$$
[H_{d}, C] = H_{d}C – CH_{d} = 0 \tag{12}
$$

なおこの $[,]$ は行列の交換子と呼ばれるもので、二つの行列 $A,B$ の積の順序を入れ替えたときの差を表します。$[A,B] = AB – BA$ です。

(12) 式を満たすとき $\frac{d}{dt} C(\{\hat{\sigma}_{i}^{z} \}) = 0$ となることが知られています ([1]) 。従って解の初期状態が $C(\{\hat{\sigma}_{i}^{z} \}) = c$ を満たしているならばすべての時刻に対して $C(\{\hat{\sigma}_{i}^{z} \}) = c$ を満たすことができます。

CQA ではこのようにして制約を満たした解のみに限定させることができます。

しかし任意の $C$ に対して (12) 式を満たす $H_{d}$ を見つけることは難しいです。そこで制約を次の (13) 式に限定した形で考えます。

$$
\sum_{i=1}^{N} \hat{\sigma}_{i}^{z} = c \tag{13}
$$

実は $H_{d}$ として (14) 式を選ぶと、(13) 式の制約に対して (12) 式を満たすことが知られています。

$$
H_{d} = -J\sum_{i,j} (\hat{\sigma}_{i}^{x} \hat{\sigma}_{j}^{x} + \hat{\sigma}_{i}^{y} \hat{\sigma}_{j}^{y}) \tag{14}
$$

ここで $\hat{\sigma}_{i}^{y}$ はパウリ行列の $y$ 成分で、これを次の (15) 式に示しました。

$$
\hat{\sigma}_{i}^{y} = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \tag{15}
$$

グラフ彩色問題の制約は (3) 式で表され、これは (13) 式の形を満たしています。よってグラフ彩色問題における CQA の $H_{d}$ は次の (16) 式となります。ここで $J$ は定数です。

$$
H_{d} = -J\sum_{i=1}^{N} \sum_{a,b} (\hat{\sigma}_{i,a}^{x} \hat{\sigma}_{j,b}^{x} + \hat{\sigma}_{i,a}^{y} \hat{\sigma}_{j,b}^{y}) \tag{16}
$$

CQA では解の初期状態、つまり driver Hamiltonian の基底状態が制約を満たしている必要があります。なぜなら CQA は時間に対して制約 $C$ の値が変化しないことを利用するので初期状態が制約を満たしていないと最終的に得られる解も制約を満たさなくなるからです。一方で (15) 式の $H_{d}$ は基底状態がグラフ彩色問題の制約を満たしていません。このような場合では以下の(17) 式で定義される項を driver Hamiltonian に対して加えることで最終的な状態が解の制約を満たしているものに限定させることができることが知られています。

$$
H_{aux} = \sum_{j} B_{j} C_{j}(\{\hat{\sigma}_{i}^{z}\}) \tag{17}
$$

ここで制約が複数個あるのでそれぞれの制約を $C_{j}$ と表しました。$B_{j}$ は各制約にかかる係数であり、これは適切に選択する必要があります。

以上がグラフ彩色問題に対する CQA の driver Hamiltonian でした。

では problem Hamiltonian について考えます。グラフ彩色問題に対する problem Hamiltonian は次の (18) 式で表されます。(18) 式は (2) 式のハミルトニアンに対して定数項などを除いたものです。なお(2) 式は古典的なハミルトニアンであり、量子アニーリングではイジング変数をパウリ行列に置き換えることが必要です。

$$
H_{p} = J \sum_{(ij) \in E} \sum_{a=1}^{q} \hat{\sigma}_{i,a}^{z} \hat{\sigma}_{j,a}^{z} \tag{18}
$$

基底状態に対するハミルトニアンの値 $E_{0}$ は次の (19) 式となります。

$$
E_{0} = m \times \{ (q-2) \times 1 + 1 \times (-1) + 1 \times (-1) \} = m(q-4) \tag{19}
$$

これは $m$ 本の各辺 $(i, j)$ に対して頂点 $i$ と頂点$j$ どちらにも割り当てられない $\sigma_{i,a}=\sigma_{j,a}=1$ となる色が $q-2$ 色あり、頂点 $i$ にだけ割り当てられる$\sigma_{i,a}=1,\sigma_{j,a}=1$ となる色が 1 色あり、頂点$j$にだけ割り当てられる$\sigma_{i,a}=-1,\sigma_{j,a}=1$ となる色が 1 色あるからです。

CQA は制約を満たした状態のみに限定するので、探索する必要のある状態数を量子アニーリング (QA) よりも減らすことができます。具体的には QA では頂点数を $N$ とすると $2^{Nq}$ 個の状態を探索する必要がありますが、CQA では $q^{N}$ 個の状態を探索するだけで済みます。このため CQA では QA よりも基底状態に到達しやすくなることが期待できます。

実験

本論文では CQA を数値シミュレーションして実験を行います。

数値シミュレーションは 4 次元ルンゲクッタ法と呼ばれる数値計算法を用いて行います。

実験に用いるグラフ彩色問題は以下の条件を満たしたものからランダムに生成します。

• 色の数：4
• 頂点の数：6
• 隣接する頂点の数：3

driver Hamiltonian について (16) 式の $a,b$ の選び方は以下の二つを用います。

• nearest-neighbor type (NN type)：$b=a+1$
• full-chain type (FC type)：$b>a$

また式 (6) のパラメータ $s(t)$ は以下の二つを用います。

• linear annealing：$s(t)=t/\tau_{\text{li}}, T=\tau_{\text{li}}$
• exponential annealing：$s(t)=1-\exp(t/\tau_{\text{ex}}), T=15\tau_{\text{ex}}$

評価指標 1

本実験では二つの評価指標を用います。

まず一つ目の評価指標は residual energy です。この評価指標では最終的な解のエネルギーと基底状態のエネルギーの差を表します。これは以下の (20) 式で定式化されます。ここで $\psi$ は最終的な解の状態を表しています。

$$
E_{res} = \bra{\psi} H_{p} \ket{\psi} − E_{0} \tag{20}
$$

評価指標 1-結果

評価指標として residual energy を用いた時の実験結果を図 5 に示しました。上の図 5 (a) が linear annealing を用いた時、下の図 5 (b) が exponential annealing を用いた時の結果です。縦軸が residual energy の値、横軸は式 (5) で出てきたアニーリングに要する時間です。

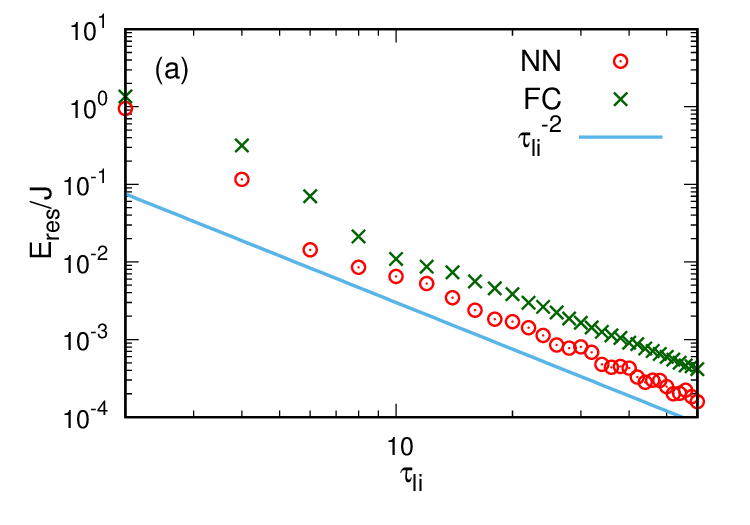
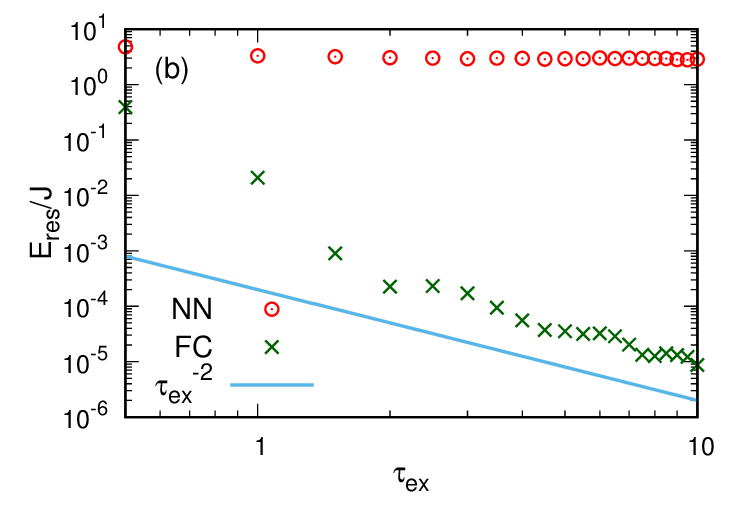
linear annealing では　$\tau_{li}$ を大きくすると NN と FC どちらも residual energy は減少しました。また NN の方が FC よりも residual energy が小さくなりました。

一方で exponential annealing では $\tau_{\text{ex}}$ を大きくすると FC の residual energy は減少しましたが、NN の residual energy は大きいままでした。

評価指標 2

二つ目の評価指標は success probability です。これは基底状態が観測される確率を表します。

success probability を求めるためにはまず解の状態を次の (21) 式のように対角化します。ここで $\ket{i}$ は頂点に割り当てられた色の組合せを表しています。

$$
\ket{\psi} = \sum_{i} c_{i} \ket{i} \tag{21}
$$

ここで状態 $\ket{i}$ が観測される確率で $|c_{i}|^{2}$ で求めることができます。よって基底状態が観測される確率はクロネッカーのデルタ $\delta$ を用いて次の (22) 式で求めることができます。

$$
p_{suc} = \sum_{i} \delta(\bra{i} H_{p} \ket{i}, E_{0}) \tag{22}
$$

評価指標 2-結果

評価指標として success probability を用いた時の実験結果を図 6 に示しました。上の図 6 (a) が linear annealing を用いた時、下の図 6 (b) が exponential annealing を用いた時の結果です。縦軸が success probability の値、横軸は式 (5) で出てきたアニーリングに要する時間です。

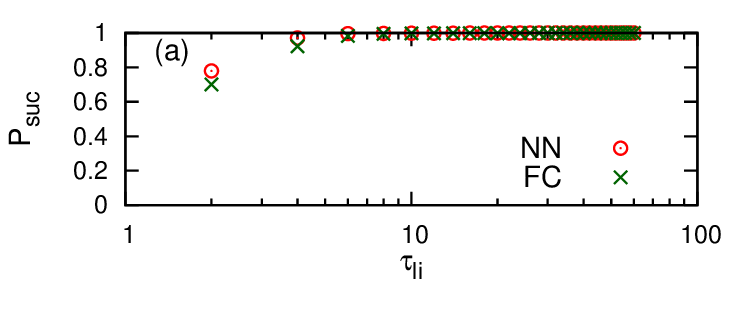
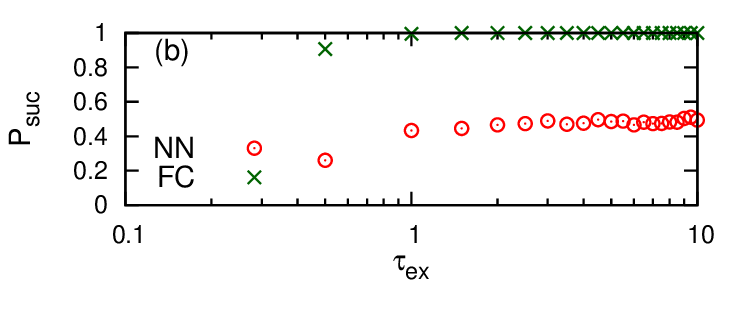
linear annealing では $\tau_{\text{li}}$ を大きくすると NN type と FC type どちらも success probability は増加しました。また $\tau_{\text{li}}$ が小さいときでは NN type の方が FC type よりも success probability が高くなりました。

一方で exponential annealing では $\tau_{\text{ex}}$ を大きくすると FC type の success probability は増加しましたが、NN type の success probability は低いままでした。

実験結果のまとめ

量子アニーリングでは次の事実が成立することが知られています。ここで $\phi_{0}(s)$ は基底状態、$\phi_{1}(s)$ は第一励起状態、$\Delta_{g}(s)$ は $\phi_{0}(s)$ と $\phi_{1}(s)$ のエネルギー差です。

アニーリング時間 $T$ が次の条件を満たすとき、励起状態が観測される確率は十分小さい。ここで $s$ は時間に関するパラメータであり $s=\frac{t}{T}$ である。

$$
T \gg \frac{\max_{0 \leq s \leq 1}|\bra{\phi_{1}(s)} \frac{dH(s)}{ds}\ket{\phi_{0}(s)} |}{\min_{0 \leq s \leq 1} \Delta_{g}^{2}(s)} \tag{23}
$$

https://doi.org/10.48550/arXiv.1806.05782

上の事実から $\Delta_{g}(s)$ が大きければ $T$ が小さくても励起状態が観測される確率が小さくなるので基底状態を求めやすくなることが分かります。

そこで本章の初めに示した driver Hamiltonian の typeである NN type と FC type について $\Delta_{g}(s)$ の値をそれぞれ求めると図 7 のようになりました。

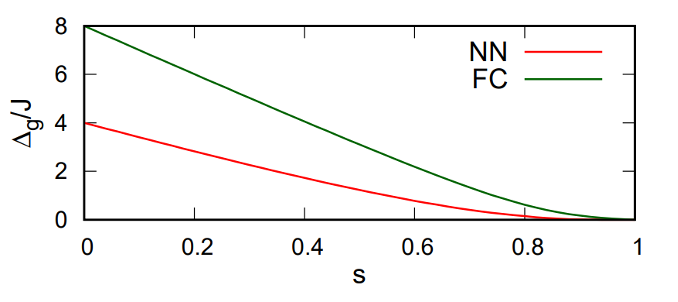
図 7 から FC type の方が $\Delta_{g}(s)$ の値が大きくなることがわかりました。よって FC type は NN type と比べて基底状態を見つけやすいことが期待されます。

一方で実験では linear annealing を用いた時に評価指標が residual energy と success probability のどちらの時でも NN type の方が性能が良くなり、「FC type の方が NN type よりも基底状態を見つけやすい」という予想に対して反している結果です。

考察

ここからは linear annealing に焦点を当てて予想と反した結果が得られた理由について考察します。

考察では図 8 に示した二つのグラフに注目します。この二つのグラフを用いて実験のとき同様 4 色のグラフ彩色問題に対して linear annealing を用いて CQA を実行します。

グラフ (b) はグラフ (a) よりも辺の数が多く、縮退度が低いです。つまりグラフ (b) はグラフ (a) より基底状態の数が少ないため、基底状態を得にくくなります。

CQA のパラメータ $s$ は上記の実験の同じものを用います。つまり、

• linear annealing：$s(t)=t/\tau_{\text{li}}, T=\tau_{\text{li}}$

です。また $\tau_{\text{li}} = 20$ は $\tau_{\text{li}} = 20$ とします。

評価指標

考察で用いる評価指標は ground-state population と呼ばれるものです。これは実験の時に評価指標として用いた success probability が最終的に得られた状態で基底状態が観測される確率で合ったのに対し、ground-state population では各 $s$ で基底状態が観測される確率を表しています。これは次式のように定式化されます。ここで $\phi_{0}(s)$ は各 $s$ の基底状態を表します。

$$
f_{g}(s) = \braket{\phi_{0}(s)|\phi_{0}(s)} \tag{24}
$$

なお理想的には常に $f_{g}(s)=1$ となります。

結果

評価指標として the ground-state population を用いた時の実験結果を図 9 に示しました。上の図 9 (a) が図 8 (a) のグラフに対する結果、下の図 9 (b) が図 8(b) のグラフに対する結果です。

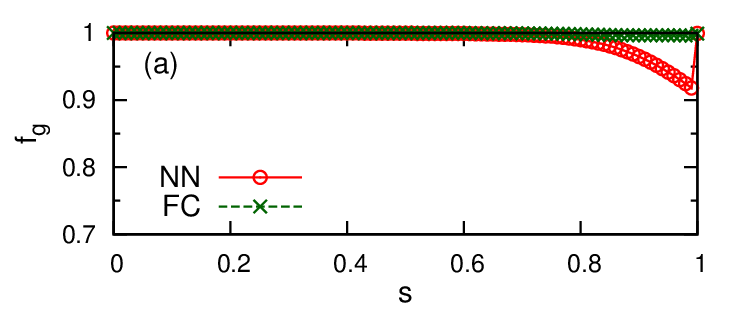
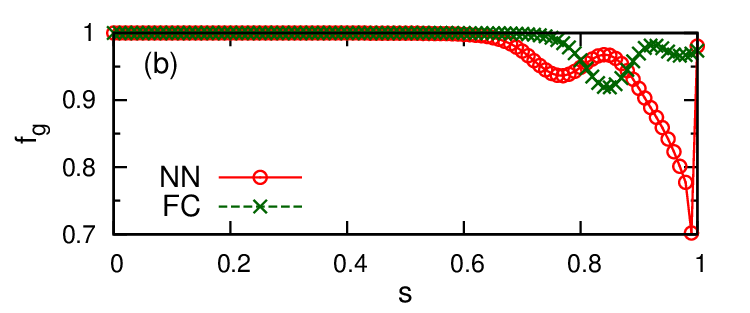
NN type のとき$s = 1 $ の直前で (a) では $f_g (s) \cong 0.9$、(b) の $f_g (s)$ はそれ以下まで $f_g$ の値が小さくなりました。

一方で FC type では (a)、(b) ともに $f_g (s)$ は高くなりました。FC type の方が $\Delta_{g}^{2} (s)$ が大きいことを考えると、この結果は (23) 式から考えた「FC type の方が NN type よりも基底状態を見つけやすくなる」という予想と一致しています。

また NN type では (a) と (b) のどちらも $s=1$ のとき $f_g (s)$ は $f_g (1)=1$ に急激に上昇していました。これはグラフ (a) とグラフ (b) どちらも基底状態が縮退しており、$s=1$ のときに励起状態が複数の基底状態のどれかに吸収されたからだと考えられます。

グラフ (b) について $s=0.8,0.9,1.0$ のときのエネルギーの分布を図 11 に示しました。左 (a) が NN typeのとき、右 (b) が FC type の時の結果です。

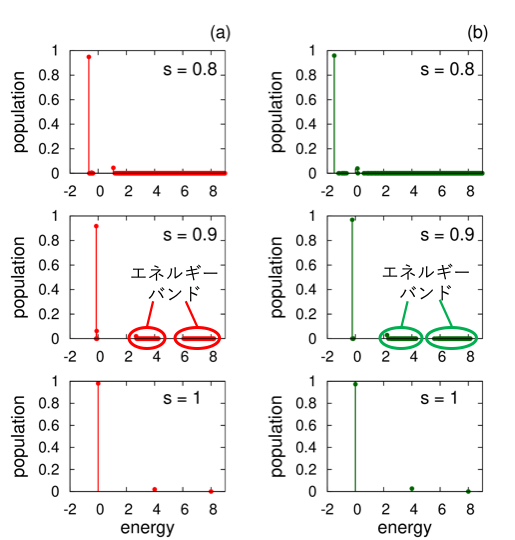
$s=0.8$ のときは NN type と FC type で似たような分布でした。$s=0.9$ のとき NN type と FC type を比較すると、NN typeでは基底状態に非常に近いが基底状態ではない部分の分布が高くなりました。$s=1.0$ では NN type と FC type どちらも励起状態が基底状態に吸収されており、これは図 9 で $f_{g}(1)=1$ となったことと一致しています。

考察：NN type がFC typeより residual energy が小さくなった理由

以上を踏まえて linear annealing で FC type より NN type の方が residual energy が小さくなった理由を考察していきます。

図 10 に着目すると $s=0.9$ では NN type と FC type どちらもエネルギー状態は基底状態と2つのエネルギーバンドが存在しています。NN type では FC type よりも基底状態と第一励起状態間のエネルギーギャップ $\Delta_{g}(s)$ が小さくなりました。しかしながら FC type の場合ではエネルギーバンド間のエネルギーギャップが NN type よりも小さくなりました。これは NN type より FC type の方が最終的 ($s = 1$ のとき) に他の励起状態に吸収されるような励起状態に広がりやすくなることを示唆しています。 この結果として FC type では高エネルギー状態の分布が広がるので residual energy が NN type よりも大きくなったと考えられます。

結論

本論文では CQA でグラフ彩色問題を解きました。

CQA は制約を満たした解のみを探索することができるので通常の QA よりも探索する必要のある状態の数が減少し基底状態に到達しやすくなることが期待できます。

実験では driver Hamiltonian として NN type と FC type を用いた場合を比較しました。結果は linear annealing で NN type の方が FC type よりも性能が良くなり、これは予想と反した結果となりました

これは量子アニーリングのまだ知られていない特性を明らかにする可能性を示唆しています。

あとがき

driver Hamiltonian を工夫することで制約を満たした解のみに限定させることができる点が面白いと感じました。

exponential annealing ではNN type を用いたとき性能が FC type と比べると著しく悪くなっていましたが、この原因の考察に興味がわきました。

また CQA と通常の QA で実際の最適化性能の差についても興味を感じました。

本記事の作成者

執筆者：原知正

メンター ：小川 立誠

参考文献

[1]：Kenichi Kurihara, Shu Tanaka, Seiji Miyashita, “Quantum Annealing for Clustering”, https://doi.org/10.48550/arXiv.1408.2035

[2] : Itay Hen, Federico M. Spedalieri, “Quantum Annealing for Constrained Optimization”,https://doi.org/10.48550/arXiv.1508.04212