敵対的生成ネットワークの性能を高める変分量子回路

Table of Contents

文献情報

タイトル : Variational Quantum Circuits Enhanced Generative Adversarial Network
著者 : Runqiu Shu, Xusheng Xu, Man-Hong Yung and Wei Cui
書籍情報 : https://arxiv.org/pdf/2402.01791

概要

敵対的生成ネットワーク(GAN:Generative Adversarial Network)は、画像を生成する深層学習(Deep Learning)の一つで、生成器(Generator)と識別器(Discriminator)から構成される。生成器は偽物の画像を作り、識別器はその画像が本物か偽物かを判定する役割があり、この二つを競わせるように学習することで、生成器から本物のような画像を生成することができるようになる。GANの課題として、生成器の表現力が高い画像を生成しようとすると、生成器と識別器を構成するニューラルネットワークのパラメータ(バイアス, 重み)の数が多くなり、その結果、ニューラルネットワークの学習回数が増えてしまうことがあげられる。そこで解決方法として論文では、新たにQCGANと呼ばれる、生成器のニューラルネットワークの一部を回転角$\theta$をパラメータに持つ変分量子回路に変えたものを紹介している。パラメータ$\theta$の変分量子回路を増やすことで、少ない量子ビットでも量子状態の表現力を高めることができる。その結果、手書き画像生成において、少ないパラメータと学習回数で、精度の良い画像を生成することが確かめられた。

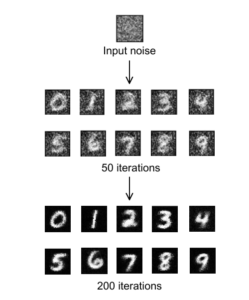
図1　QCGANによる手書き文字の生成画像

図1はQCGANに入力ノイズ(input noise)を入力して、学習50回目(50 iterations)と学習200回目(200 iterations)の手書き文字の生成画像(サイズ28×28、784ピクセル)を表す。学習回数が増えると手書き数字が鮮明になっていく様子が確認できる。

実験手法

論文では、新たにQCGAN(Quantum-classical GAN)というものを導入している。QCGANは、GANと同様に生成器と識別器から構成され、異なる点はQuantum Generator(以下、量子生成器とする)が量子ビットから成る変分量子回路とニューラルネットワークのハイブリットで構成されている点である。

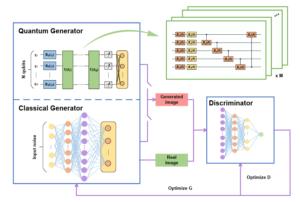
図2　古典的なGANとQCGANの構造

QCGANの仕組みはGANとほぼ同じなので、詳しい仕組みは、Appendixを参照してもらいたい(Appendix.1)。ここでは、生成器の中身を説明する。生成器で行われていることは、以下の①から④の過程から成る。

①エンコーディング

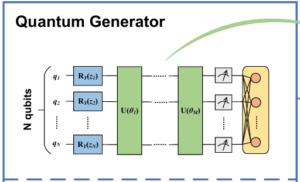
図3　QCGANの生成器の構造

1. 潜在変数$z$の要素数の量子ビットを用意する。
2. 潜在変数$z$の要素の値を量子ビットの回転角に対応させる。
3. 初期状態$\ket{0}$の基底状態の量子ビットにy軸を軸として角度$z_i$回転させる演算子$R_y(z_i)$を作用させる(Appendix.3)。
$$\begin{align*}
\ket{\psi_z} = \overset{N}{\underset{i=1}\otimes} R_{y}(z_{i}) \ket{0}
\end{align*}
$$

②変数の進化

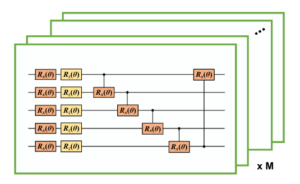
図4　QCGANの生成器を構成する変分量子回路の構成

次に、Encodingされた量子ビットに回路UをM回作用させる。UはX軸回転ゲートとZ軸回転ゲートで構成されており、いずれの回転ゲートも量子ビットの向きを$\theta$回転させる。CNOTゲートは2入力量子ビットで、量子状態の数を増やす役割がある(Appendix.3)。 $V(\theta)$はUがM個から成る回路で、①, ②の操作を式にまとめると以下の式になる。
$$\begin{align*}
\ket{\psi_z, \theta} = V(\theta)\ket{\psi_{z}} = V(\theta) \overset{N}{\underset{i=1}\otimes} R_{y}(z_{i}) \ket{0}
\end{align*}$$

③計測と更新

この操作では、始めに反応後の量子ビットを計測する。この時、計測後の値の数は、潜在変数$z$の要素数と一致する。なぜなら、潜在変数に対応する量子ビットの数は不変だからである。しかし、これでは768ピクセルの画像を出力できないので、次に計測値をニューラルネットワークに入力し、生成画像を出力させる。

④生成器の学習

QCGANの学習方法は、GANと同様に誤差逆伝播法(BP:Back-Propagation)で学習可能である。このようにして、ニューラルネットワークのパラメータ(バイアス、重み)と変分量子回路のパラメータ$\theta_i (i = 1, 2, \ldots , M)$を更新する。

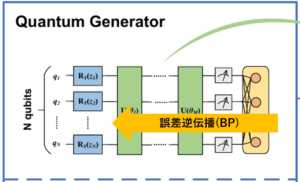
図5　変分量子回路の学習方法

以上①～④の過程をMindSpore Quantumと呼ばれるフレームワークで実装し[1]、MNISTの手書き文字画像を使ってQCGANを評価する。評価には、Fréchet Inception Distance*(FID)を使った。(Appendix.2)

実験結果

表1　QCGANとその他の古典的なGANの生成器における層の構造とパラメータ数

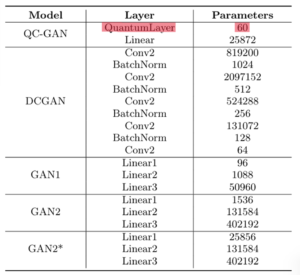
この表は、実験で用いた様々な種類のGANの層(Layer)の数とパラメータ(Parameters)の数を表している。QCGANのパラメータの数が他より少ないことに注目してほしい。特に、QuantumLayerのパラメータの数が60で少ないのが顕著である。

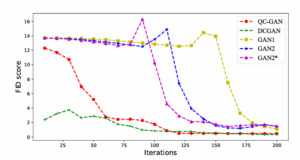
図6　QCGANとその他の古典的なGANにおける学習回数に対するFID値の変化

図6のグラフは、横軸を学習回数(Iterations)、縦軸をFID値にしたときのそれぞれのGANの振舞いを表す。FIDは画像の類似度を表す指標である(Appendix.2)。赤線のQCGANと緑線の深層畳み込み敵対的生成ネットワーク(DCGAN:Deep Convolutional GAN)がすぐにFID値が小さくなっているとわかる。つまり、少ない学習回数で本物そっくりな画像を生成できることを示す。また、表1よりQCGANとDCGANのパラメータ数を比べると、QCGANの方がパラメータの数が小さいことがわかる。つまり、QCGANは学習時間を小さくすることができることが示された。さらに、論文では、生成器のパラメータ数が768のとき、QCGANの潜在変数は100でGAN2の潜在変数は5であったことが確認された。一般的に、潜在変数が大きくなると、特徴量が増えて多様な画像を生成することにつながる。QCGANにはそのような性能もあることが示された。

まとめ

本論文では、GANの生成器を量子ビットとニューラルネットワークのハイブリットで構成される変分量子回路に変えたQCGANを用いて手書き画像を生成し、従来からある数々のGANと伴に、FID値で画像の性能と学習回数を比較した。その結果、QCGANは他の種類のGANよりも少ないパラメータと学習回数で画像を生成することが可能であるとわかった。このことから、変分量子回路を用いた画像生成モデルは、パラメータの数を減らし、学習速度を向上させることが期待できる。

Appendix

Appendix.1 GANの仕組み

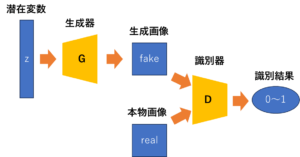
図7　GANの全体像

図7のようにGANは、画像を作り出す生成器と、生成画像と本物画像を判定する識別器から成る。
識別器は、本物画像に対して1(True)を出力し、生成画像に対して0(False)を出力するように学習する。
一方、生成器は、*潜在変数$z$から生成画像を作り、識別器に本物画像であるとだます(つまり、識別器に1(True)と判定させる)ように学習する。

*潜在変数(ノイズ, ノイズベクトル): 観測データに直接現れないが、データ生成プロセスに影響を与える潜在的な要因を表す変数。

潜在変数は、平均0、分散1の標準正規分布からサンプリングされる。
図8は、生成器を構成するニューラルネットワークの概略図である。簡単化のため、隠れ層の数は1つにして描いている。
入力層の値から出力層の値に向けて、重み$w$をかけた値の和をとり、閾値であるバイアス$\theta$を引いた後、活性化関数に通すことを繰り返す。今回利用したMNISTの場合では、生成器は20～100程度のベクトルの要素から成る潜在変数Zを入力し、784ピクセルの画像データを出力する。

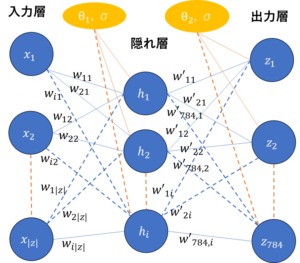
図8　生成器(Generator)の構造

図9は識別器を構成するニューラルネットワークの概略図である。
識別器は、784ピクセルの画像データを入力し、そのデータが本物画像であるか(判定値1)、生成画像であるか(判定値0)判定するため出力層は1つである。

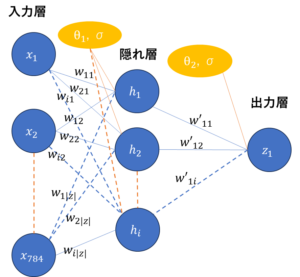
図9　識別器(discriminator)の構造

次に、GANの学習方法を説明する。
始めに、生成器と識別器を構成するニューラルネットワークのパラメータ($w$, $\theta$)の値をランダムに設定する。次に、識別器の学習を行う。生成器で画像を生成した後、識別器に通す。この時、パラメータをランダムに設定したので、識別器の判定はでたらめである。そこで、図10のように損失関数を用いて*誤差逆伝播法で、識別器が正しく画像を判定するようにパラメータを調節する。これによって、識別器は、生成画像と本物画像を正しく見分けられるようになる。

*誤差逆伝播法: 出力層から入力層に向かって、勾配(誤差の変化率)を計算し、その計算結果を基にパラメータを調節することで正解の値と予測値の差を小さくさせるアルゴリズム。

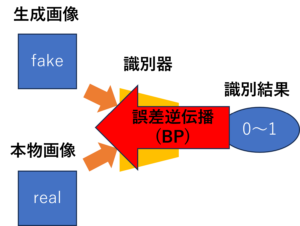
図10　識別器の学習

識別器の損失関数:
$$
\begin{align}
&L_{D} = -\ \left( \ \frac{1}{m} \sum_{i = 1}^{m}\ [\log D(\vec{x_{i}}) + \log (1 – D(G(\vec{z_{i}}))])\right) \tag{1} \\
&m:\ 画像データの数,\ \vec{x}:\ 本物画像データ\\
&G(\vec{z}):\ 潜在変数から求めた生成画像データ\\
&D(\vec{x}):\ 本物画像データの判定値(0 or 1)\\
&D(G(\vec{z})):\ 生成画像データの判定値(0 or 1)
\end{align}
$$

目標は損失関数の値が0になるように学習することである。識別器は本物画像を$D(\vec{x})=1$、生成画像を$D(G(\vec{z}))=0$と判定するので、この損失関数に代入すると0になり、目標を達成する。次に、図11のように生成器が学習済みの識別器をだますように(つまり、識別器に生成画像を1と判定させる)、ニューラルネットワークのパラメータを調節する。具体的には、識別器のパラメータ($w$, $\theta$)を固定して、生成器の損失関数を用いて誤差逆伝播法で生成器を学習する。

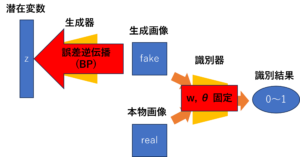
図11　生成器の学習

生成器の損失関数:
$$
\begin{align}
L_{G} = -\ \left( \ \frac{1}{m} \sum_{i = 1}^{m}\ [\log D(G(\vec{z_{i}}))]\right) \tag{2}
\end{align}
$$
目標は損失関数の値が0になるように学習することである。生成器は識別器に生成画像を本物画像であると誤判定させたいので、$D(G(\vec{z}))=1$と判定し、この損失関数に代入すると0になり、目標を達成する。このようにして、GANでは、識別器と生成器の学習を競わせることで、生成器で画像を生成することが可能になる。
最後に、上記の損失関数を一つの式にまとめて、全体の学習目標を示した目的関数を説明する。以下がそのGANの目的関数である。

$$
\begin{align*}
\underset{G} \min\ \underset{D} \max\ V(D, G) = E_{x \sim P_{data(x)}}[\log D(\vec{x})] + E_{z \sim P_{z(z)}}[\log (1 – D(G(\vec{z})))] \tag{3}
\end{align*}
$$

第1項は本物画像データに関する期待値で、第2項は生成画像データに関する期待値である。式では、識別器は第1項と第2項の和を最大化することを目標にし、生成器は第2項を最小化することを目標にしていることを表す。
まず、式(3)の目的関数から式(1)の識別器の損失関数について説明する。
図12は、式(3)に含まれる対数関数をグラフにした図である。識別器の場合、式(3)の値を最大化させたく、識別器の判定が正しい時、$D(G(\vec{z}))=0$, $D(\vec{z})=1$となり、式(1)は0に近づいて最大化する。

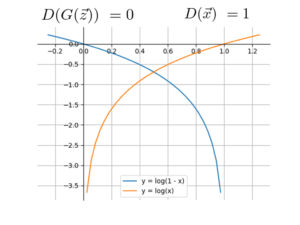
図12　識別器についての目的関数

次に式(3)の目的関数から式(2)の生成器の損失関数について説明する。式(3)では、値を最小化させたく、生成器が識別器をだます時、$D(G(\vec{z}))=1$となり、この時、式(3)は$-\infty$になり、最小になってる。しかし、学習始めの勾配が緩やかで、学習が進まない可能性があるので、損失関数には、図14のように、$log(x)$を用いている。よって、生成器の損失関数は式(2)のようになる。

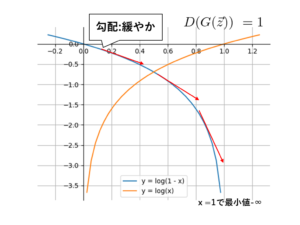
図13　生成器についての目的関数

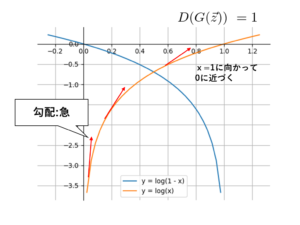
図14　生成器の損失関数との対応

Appendix.2 FID値

FID(Fréchet Inception Distance)値は、本物画像と生成画像の類似度の値で、生成画像が本物画像に似ているほど、FID値は小さくなる。
FID値をもとめる式は
$$
\begin{align*}
&FID(x, g) = ||\mu_x – \mu_g||_2^2 + Tr(\sigma_x + \sigma_g – 2(\sigma_x \sigma_g)^{0.5}) \\
&\mu_x:\ 本物画像データの特徴量の平均(ベクトル) \\
&\sigma_x:\ 本物画像データの特徴量の分散(ベクトル) \\
&\mu_g:\ 生成画像データの特徴量の平均(ベクトル) \\
&\sigma_g:\ 生成画像データの特徴量の分散(ベクトル)
&\end{align*}
$$
と表される。第1項は$L^2$ノルムで、第2項は$\sqrt{\sigma_x}$と$\sqrt{\sigma_g}$の差の共分散行列をトレースをとった値である。
求め方は、まず、*Inception-v3という学習済みのモデルに本物画像データを入力して、画像の特徴量を抽出する。同様に、生成画像の特徴量も抽出する。次に、本物画像データの特徴量の分布をガウス分布とみなして、平均と分散をもとめる。生成画像データについても同様にもとめる。それらをFIDの式に代入して、値をもとめる。

*Inception-v3: 画像データを入力して、画像の特徴量を出力する学習済みのモデル

Appendix.3 量子ゲート

量子ビット(Qbit)は、古典的なビットのような0か1の2値ではなく、観察されるまで0と1の状態が重なっている(重ね合わせの状態)。
この重ね合わせの状態$\ket{\psi}$を式で表すと
$$
\begin{align*}
&\ket{\psi} = \alpha \ket{0} + \beta \ket{1}
= \left[
\begin{array}{cccc}
\alpha\\
\beta
\end{array}
\right] \\
&|\alpha|^2 + |\beta|^2 = 1 \\
&\alpha,\ \beta:\ 複素数 \\
&\ket{0},\ \ket{1}:\ 複素数ベクトル
\end{align*}
$$
となる。$|\alpha|^2 $は観察されたとき0を返す確率を示し、$|\beta|^2$は観察されたとき1を返す確率を示す。そのため、$\alphaと\beta$は、0と1の起こりやすさを表すので、確率振幅と呼ばれる。
次に0と1の重ね合わせの状態を単位球面上で視覚的に表現されたブロッホ球(Bloch sphere)を紹介する。

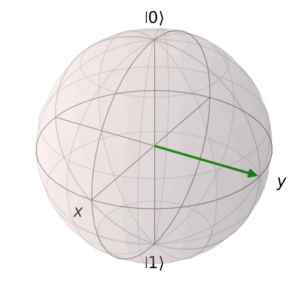
図15　ブロッホ球の例

例えば、$\ket{\psi} = \frac{1}{\sqrt{2}} \ket{0} + \frac{i}{\sqrt{2}} \ket{1}$をブロッホ球で表したのが図15である。
これを踏まえて、回転ゲートを説明する。今回の変分量子回路に使われた回転ゲートは、x軸回転ゲート、y軸回転ゲート、z軸回転ゲートである。
x軸回転ゲートは、x軸を軸にして、量子ビットを任意の角度$\theta$回転させる働きがある。行列で表すと、
$$
R_x(\theta) = \left[
\begin{array}{cccc}
\cos \frac{\theta}{2} & -i \sin \frac{\theta}{2}\\
\\
-i \sin \frac{\theta}{2} & \cos \frac{\theta}{2}
\end{array}
\right]
$$
となり、状態$\ket{\psi}$の行列と積をとることで、量子ビットがx軸ゲートを通った後の状態をもとめることができる。
同様にして、y軸ゲートは、y軸を軸として量子ビットを回転させて、その行列は、
$$
R_y(\theta) = \left[
\begin{array}{cccc}
\cos \frac{\theta}{2} & -\sin \frac{\theta}{2}\\
\\
\sin \frac{\theta}{2} & \cos \frac{\theta}{2}
\end{array}
\right]
$$
である。zゲートは、z軸回転でその行列は
$$
R_z(\theta) = \left[
\begin{array}{cccc}
e^{-i \frac{\theta}{2}} & 0\\
\\
0 & e^{i \frac{\theta}{2}}
\end{array}
\right]
$$
である。最後に二つの量子ビットに作用させるCNOTゲートを説明する。

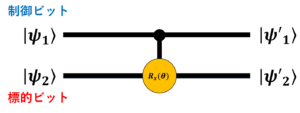
図16　CNOTゲート

$\ket{\psi’_1}$は、$\ket{\psi_1}$を出力する。 $\ket{\psi’_2}$は、まず$\ket{\psi_1}$と$\ket{\psi_2}$のテンソル積をとる。
$$
\begin{align*}
\ket{\psi_1} \otimes \ket{\psi_2} &= (\alpha_1 \ket{0} + \beta_1 \ket{1}) \otimes (\alpha_2 \ket{0} + \beta_2 \ket{1})\\
&= \alpha_1 \alpha_2 \ket{00} + \alpha_1 \beta_2 \ket{01} + \beta_1 \alpha_2 \ket{10} + \beta_1 \beta_2 \ket{11}\\
&=\left[
\begin{array}{cccc}
\alpha_1 \alpha_2\\
\alpha_1 \beta_2\\
\beta_1 \alpha_2\\
\beta_1 \beta_2
\end{array}
\right]
\end{align*}
$$
次に、図16の制御ビットが$\ket{0}$の時は何も操作せず、制御ビットが$\ket{1}$の時は、標的ビットにx軸回転ゲートを作用させる。
この過程は行列では、
$$
U_{CNOT\ R_x} =
\left[
\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & \cos\frac{\theta}{2} & -i \sin\frac{\theta}{2}\\
0 & 0 & -i \sin\frac{\theta}{2} & \cos\frac{\theta}{2}
\end{array}
\right]
$$
と表され、二つの量子ビットのテンソル積の後にこの行列と積をとることで、CNOTゲートを作用させたことになる。テンソル積の計算結果を見ると、ベクトルの要素数が2つから4つに増えている。これは、量子状態が2つから4つになることを表している。パラメータ$\theta$を持つCNOTゲートを何度も作用させることで量子状態を増やすことができるので、使用するパラメータ$\theta$の種類を少なくても古典的なニューラルネットワークと同等の表現力を持つことが可能になる。

参考文献

[1] https://gitee.com/mindspore/mindquantum/tree/research/paper_with_code

あとがき

本論文では、GANの生成器の部分に変分量子回路を用いたQCGANだけでなく、GANの生成器と識別器に変分量子回路を用いたQuGANも紹介している。しかし、結果ではQuGANの生成が画像は不鮮明であることが多かった。このように変分量子回路の能力が発揮される場面には条件があるように思える。今後は、画像生成モデルに条件を変えて変分量子回路を組み込むことで生成画像の向上の原因を明らかにし、その有効性を示すことが求めらる。

本記事の担当者

嶋﨑司晃

Post Views: 106