文献情報
- タイトル:Power network optimization: a quantum approach
- 著者:Giuseppe Colucci, Stan van der Linde, and frank Phillipson
- 書誌情報:https://doi.org/10.1109/ACCESS.2023.3312997
概要
電力ネットワーク全体で電力を効率的に使用するためには電力の余剰の最適化が重要な要素です。本論文では、量子アニーリングを用いて電力余剰を最適に活用できるようなネットワークを探索する方法を示しました。そして、ドイツの送電ネットワークでの電力余剰を最適化するという問題に対して、量子と古典のハイブリッドソルバーと古典ソルバーのそれぞれで結果を出して、古典ソルバーに対して量子と古典のハイブリッドソルバーがコスト関数の値がより低い解を出すことを示しました。
背景
電力ネットワークとは発電所で作られた電力を全国まで送るために結ばれる電力系統のことです。本論文においては特に、ある地域が複数の地区に分割されていて、その地区内の地点同士で電力を共有しているようなネットワークのことを指しています。本記事において地域、地区、地点の使い方については図1のとおりで、地区は地点の集合、地域は地区の集合という意味で用いています。ここで電力ネットワークを最適化するとは、地域全体で総電力余剰を最小化することを指します。総電力余剰の最小化とはつまり、地点によって電力余剰の大小がある中で、その地点をまとめて地区として電力を共有することで、電力余剰の大きい地点から電力余剰が小さい地点に電力が送られて地区や地域としてみた時に電力の余剰が小さくなった状態のことです。本論文ではそのようなネットワークの中で構築するコストが最小のものを探索します。
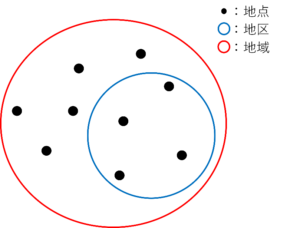
図1: 地点・地区・地域を表す図
問題
本論文では電力ネットワークの最適化をグラフ分割問題として設定します。グラフとは頂点と、頂点同士の関係を辺として表したデータ構造のことです。また、グラフ分割問題とは図2に示したように、ある1つのグラフに対し分割数を設定して、与えられた制約を守りつつコストを最小化(最大化)できるような分割方法を探る問題のことです。このとき、分割された後のそれぞれの部分をクラスタと呼びます。本論文では、頂点を地点、辺を2つの地点の間の送電線、クラスタを地区としてグラフを考えます。そして最小化するためのコストは送電線を構築するのにかかるコストとして設定します。地点における電力余剰はその地点を示す頂点の重みによって符号化されます。また、地区や地域の総電力余剰はそれらの和として表されます。また、構築するコストは辺に対して重みをつけることで考慮することができます。以上のようなグラフの中で、それぞれのクラスタ(地区)での重みの総和(総電力余剰)をある一定値以下に抑えつつ、構築するコストが最小のものを探索します。
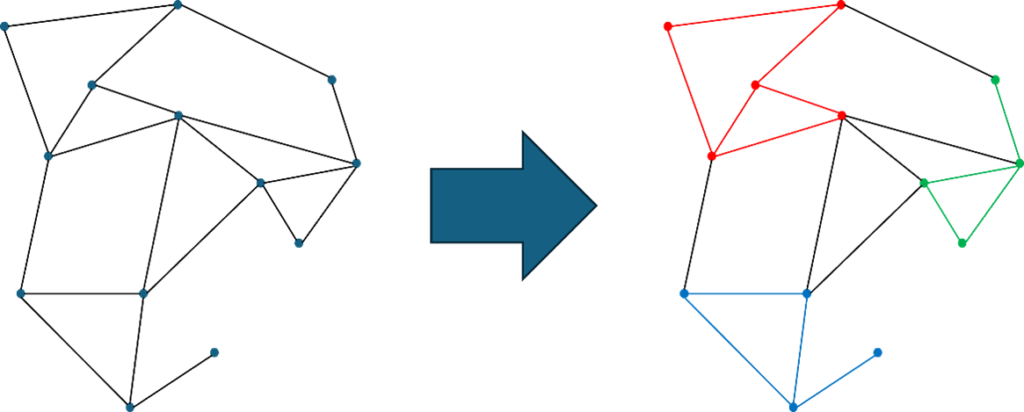
図2: グラフ分割問題を表す図
方法
グラフ分割問題は、NP困難と呼ばれる古典コンピュータでは解くことが難しい問題です。量子アニーリングでは、グラフ分割問題をコスト関数の最小化問題として定義することで解くことができるようになります。以下では、まず、問題で述べた電力ネットワークの最適化問題を数学的に定式化する方法を説明します。その後、実際に量子アニーリングハードウェアを用いて解くためにQUBO定式化と呼ばれる定式化を行います。最後に、ドイツの送電データを用いて問題設定をし、カナダにあるD-Wave社が提供するハイブリッドソルバーのCQMおよびBQMと、Azure Quantumで利用可能な古典ソルバーのパラレルテンパリング(PT)、シミュレーテッドアニーリング(SA)、サブストキャスティックモンテカルロ(MC)およびタブーサーチ(TS)で、どれがよりコスト関数値が低い解を出せるかで比較しました。それぞれのソルバーについての説明は以下のとおりです。また、問題設定に用いたデータはSciGRIDと呼ばれる欧州送電網のオープンソース参照モデルです。
- D-Wave CQM: CQMはConstrained Quadratic Modelのことで制約付き二次モデルを意味します。すなわち、制約を表す式を別に持つ、二次のコスト関数の最小化問題です。変数については2値および整数値のどちらでも定義可能です。
- D-Wave BQM: BQMはBinary Quadratic Modelのことでバイナリ二次モデルを意味します。すなわち、二次のコスト関数の最小化問題です。変数については二値のみで定義可能です。
- PT: パラレルテンパリングとは別名レプリカ交換モンテカルロ法のことで、異なる温度で様々な分布をまとめ、その分布の集まりをシミュレーション計算の対象とすることで、マルコフ連鎖モンテカルロ法のサンプリング効率の改善を図ろうとしたものです。
- SA: シミュレーテッドアニーリングとは別名焼きなまし法と呼ばれ、高温状態の金属の温度を徐々に下げると、秩序ある構造が作り出されるという技術をコンピュータ上で再現したアルゴリズムです。
- MC: サブストキャスティックモンテカルロとは拡散モンテカルロと呼ばれるもののひとつで、確率分布に従いpopulationを増やしたり捨てたりし、それによる確率分布の変化を追うものです。
- TS: タブーサーチとは人工知能の概念に基づいた局所探索法を一般化したものです。基準から近傍のサンプルを複数生成し、その中から最良のサンプルを選び出します。そしてそのサンプルで同様の操作を繰り返します。ただし、複数サンプルから最良のサンプルを選び出すという操作を毎回タブーリストに追加し、その操作によるサンプル生成を行わないようにします。以上のようなアルゴリズムです。
数学的定式化
問題で述べたグラフについて、グラフ$G=(V,E)$として頂点$V$を地点、辺$E$を2つの地点間の送電線とします。また、$P$をクラスタ(地区)の数、$N=|V|$をグラフの頂点(地点)の数とします。そして2値変数$v_{np}$を頂点$n$がクラスタ$p$にある時に$1$、そうでないときに$0$を表すものとします。$w_n$を頂点$n$における電力余剰を表す定数、$k$をクラスタ間での電力余剰の偏りをなくすための値を示す定数、$\alpha$と$\beta$をそれぞれ1つのクラスタ内とクラスタ間の送電コストを表す定数として定義します。すると目的関数と制約は以下のように表されます。
$$
\tag{1}
\min_{\boldsymbol{v} \in \{0,1\}^{PN}} \sum_{p=1}^{P} \left\{ \alpha \left( \sum_{n=1}^{N} v_{np} \right)^2 + \beta \left( |E|\, – \sum_{\{n,m\} \in E} v_{np} v_{np} \right) \right\}
$$
$$
\tag{2}
\sum_{p=1}^{P} v_{np} = 1, \quad n = 1, \ldots, N
$$
$$
\tag{3}
\sum_{n=1}^{N} v_{np} w_n – k \sum_{n=1}^{N} v_{np} \leq 0, \quad p = 1, \ldots, P
$$
(1)式で表される目的関数は二つの項で構成されます。第一項は、一つのクラスタ内における送電線の総構築コストを表し、第二項はクラスタ間での送電線の総構築コストを表します。(2)式と(3)式はそれぞれ制約を表します。(2)式の制約はOne-hot制約といい、各頂点が一つのクラスタにのみ属することを強制します。(3)式の制約はBalancing制約といい、クラスタ間での電力の余剰の偏りが大きくなることを防ぐ制約です。$k$は電力の余剰の偏り度合いを表す変数で、この値が大きいほど、より大きい偏りを許容することとなります。
QUBO定式化
(1)から(3)で示した数式はCQMと呼ばれる制約付き二次モデルの形です。この状態を入力として解けるソルバーもありますが多くの量子ソルバーではこの形では解けません。よってこれをQUBOの定式化により変換する必要があります。この時、目的関数と制約は以下のような形となります。
$$
\min_{\boldsymbol{x} \in \{0,1\}} H \left(\boldsymbol{x}\right) + \sum_{i=1}^{\#\text{constraints}} \lambda_i P_i\left(\boldsymbol{x}\right)
$$
この式について、$H\left(\boldsymbol{x}\right)$はハミルトニアンのことで目的関数に対応しています。また、$\lambda_i P_i \left(\boldsymbol{x}\right)$はペナルティ項と呼ばれ、制約を表しています。ここで、$\lambda_i $はハイパーパラメータと言いそれぞれの制約を強制する強さを表現します。以上のことを踏まえて(1)から(3)式を変換するとQUBO最適化問題は以下のようになります。
$$
\min_{\left(\boldsymbol{v},\boldsymbol{x}\right) \in \{0,1\}^{PN} \times \{0,1\}^{PN}} H\left(\boldsymbol{v}\right) + \lambda_{oh} P_{oh} \left(\boldsymbol{v}\right) + \lambda_{bc} P_{bc} \left(\boldsymbol{v}, \boldsymbol{x}, K \right)
$$
ただし、
$$
\tag{4}
H\left(\boldsymbol{v}\right) = \sum_{p=1}^P \left\{\alpha\left(\sum_{n=1}^N v_{np} \right)^2 + \beta\left(|E| \, – \sum_{\{n,m\} \in E} v_{np} v_{mp} \right)\right\}
$$
$$
\tag{5}
P_{oh}\left(\boldsymbol{v}\right) = \sum_{n=1}^{N} \left(\sum_{p=1}^{P}\boldsymbol{v}_{np} \, – \, 1\right)^2
$$
$$
\tag{6}
P_{bc}\left(\boldsymbol{v},\boldsymbol{x},K\right) = \sum_{p=1}^P \left(\frac{2^K – \frac{1}{2}\,}{c} \left(c + \sum_{n=1}^N \boldsymbol{v}_{np}\left(\boldsymbol{w}_n \, – \, k \right)\right) – \sum_{a=0}^{K-1}2^a\boldsymbol{x}_{ap}\right)^2, \quad c = \frac{1}{2}\sum_{n=1}^N \left(\boldsymbol{w}_n \, – \, k \, – \, |\boldsymbol{w}_n \, – \, k|\right)
$$
以下では最適化問題の各項についてその導出方法を説明します。まず、(4)式で表されるハミルトニアンですが、これは(1)式で表される元の目的関数がQUBOの形式に準拠していたためそのまま導出することができます。次に、(5)式について、これは(2)式で表されるOne-hot制約と同じ意味を示すように式変形が為されています。すなわち、(2)式で表される等式を満たすときのみ(5)式の値は$0$となり、それ以外では必ず正の値を取ります。(6)式についても同様で、Balancing制約の(3)式の不等式を満たすときに(6)式の値はより小さくなるようになっています。(6)式が複雑となっているのは元の制約が不等式だからです。さらに変数が整数だけでなく小数が使われるため、このような形となっています。制約が等式であれば、移項して2乗することで(5)式のように簡単に導出することができますが、不等式制約ではそのようにすることはできません。一般に、変数が整数の時は、スラック変数と言われる変数を用いると1つの不等式制約を2つの等式制約に変形することができます。これに少しの工夫を加えて小数も扱えるようにしたのが(6)式です。(6)式の$K$はハイパーパラメータでこの値が大きいほど精度は高くなります。
実験
本論文では3つの実験を行いましたが、本記事ではそのうちの1つを取り上げます。実験ではSciGridと呼ばれる欧州送電網のオープンソースを用いました。このオープンソースを基にドイツの電力ネットワークを表すグラフを構築し、そのグラフに対して2~9分割のグラフ分割問題を解き、そのときのコスト関数の値を比較しました。SciGridを基に作成したドイツの電力ネットワークを表すグラフが以下のとおりです。
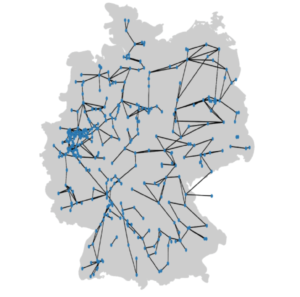
図3: SciGRIDを基にしたドイツの電力ネットワークのグラフ https://doi.org/10.1109/ACCESS.2023.3312997
本実験におけるパラメータの値は以下の通りとしました。
- $\alpha = 1$
- $\beta = 10$
- $k = 0.5$
また、各頂点における電力余剰は一様分布$[0,1)$から決定することとし、ハイパーパラメータの$\lambda_{oh}$と$\lambda_{bc}$は表1のように設定しました。そして、もう1つのハイパーパラメータである$K$について、$K=10$とするとバランシング制約のエラーを検知するのに十分で、オーバーフローの点でも問題がないことを確認できたため、$K=10$として設定しました。
表1: 各クラスタ数におけるハイパーパラメータの値
| $P$ | $\lambda_{oh}$ | $\lambda_{bc}$ |
|---|---|---|
| 2 | 500 | 0.01 |
| 3 | 300 | 0.08 |
| 4 | 270 | 0.2 |
| 5 | 250 | 0.2 |
| 6 | 240 | 0.4 |
| 7 | 230 | 0.9 |
| 8 | 230 | 0.9 |
| 9 | 290 | 1.0 |
結果
ハイブリッドソルバー(CQM, BQM)と古典ソルバー(PT, SA, MC, TS)のそれぞれで出した結果が以下のとおりです。
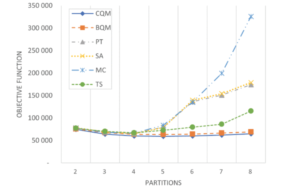
図4: ハイブリッドソルバーと古典ソルバーのそれぞれを用いて出した結果を表すグラフ https://doi.org/10.1109/ACCESS.2023.3312997
グラフについて、縦軸はコスト関数の値、横軸はクラスタの数を表します。このグラフからわかることとして、ハイブリッドソルバーのBQMおよびCQMではほかの古典ソルバーに比べてコスト関数の値が小さく、また、その差はクラスタの数が大きくなるに従い顕著となります。
以下はクラスタの数を6としたときにCQMによって得られた解の例です。これを見ると、クラスタによっては互いに離れた点が生成されてしまっています。これは、目的関数のパラメータであるクラスタ間の送電コストを表す$\beta$が定数であることに起因すると考えられます。改善する方法としては、これをクラスタ間の地理的距離を表す関数として定義することが挙げられます。
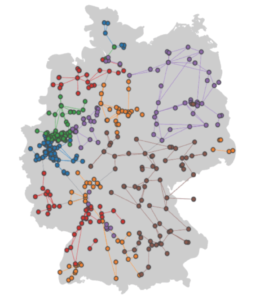
図5: 得られた結果の一例
https://doi.org/10.1109/ACCESS.2023.3312997
結論
本論文では、電力余剰を最適化できるような電力ネットワークを量子アニーリングを用いて構築する方法を提案し、実際のドイツのデータを用いて作成した電力ネットワークにおいてそれを適用し、古典ソルバーによって解いた結果と比較しました。その結果、量子と古典のハイブリッドソルバーでは古典ソルバーに比べ、コスト関数が低い値を出すという点で優れていることが分かりました。また、クラスタの数が大きくなるにしたがって、コスト関数値の差も大きくなることが分かりました。このことから、より大規模で複雑なネットワークを構築するより良い方法として量子アニーリングが用いられることが期待できます。
あとがき
本論文では、量子と古典のハイブリッドソルバーが電力ネットワークの最適化に有効であることが示されました。しかし、ビット数の制限により、量子アニーリング単独と古典ソルバーの比較は行われておらず、その有効性についても言及されていませんでした。また、本記事ではクラスタ間での電力移動がない場合に焦点を当てて紹介しましたが、論文内ではクラスタ間の電力移動を考慮した定式化も行われていました。ただ、この場合、扱う変数の数が増大するため、定式化にとどまり、実験は実施されていませんでした。今後、量子アニーリング技術が発展し、より大規模な問題を解決できるようになれば、本論文で行えなかった量子アニーリング単独と古典ソルバーの比較や、クラスタ間の電力移動を考慮した電力ネットワークの最適化が可能になると考えられます。その結果、電力ネットワーク最適化における量子アニーリングの有効性は、さらに明らかとなるでしょう。
本記事の作成者
山田竜雅