文献
- タイトル: Finding Maximum Cliques on the D-Wave Quantum Annealer
- 著者: Guillaume Chapuis, Hristo N. Djidjev, Georg Hahn, Guillaume Rizk
- URL: https://arxiv.org/abs/1801.08649
概要
あるグラフの部分グラフのうち、それに含まれる任意の二点間に辺があるような部分グラフで最大のものを最大クリークと呼ぶ。与えられたグラフから最大クリークを発見する問題は最大クリーク問題と呼ばれており、これはNP困難であると知られている。本論文はこの最大クリーク問題のD-Wave 2Xを用いた解法について述べている。
解き方
グラフをG=(V, E)と表し、Vは点の集合、Eは辺の集合とする。グラフGに対して、辺のある二点間の辺をなくし、辺のない二点間に辺を張った(辺の集合Eに対して補集合$\overline{E}$を考える)グラフH=(V, $\overline{E}$)を考える。このとき、グラフHの独立集合S (どの二点間も辺で継がられてない点の集合)はグラフGではクリークに他ならない。つまり、最大クリーク問題と最大独立集合は表裏一体の関係となっており、このことを利用してグラフG最大クリークを求めるために、グラフHの最大独立集合問題を見つけることを試みる。
この問題の読み替えは、のちで用いる変数の数や目的関数の表現をより簡便にする意味がある。
最適化問題の定式化
被最適化変数: $x_{i} \in \{0, 1\}, i \in V$ (i番目の頂点が求める最大独立集合に含まれていれば1, そうでない場合は0)
目的関数:
目的関数の第1項は最大独立集合に含まれる点数が大きければ目的関数を小さくし、第2項は辺で結ばれる2点をどちらも最大独立集合に含めると目的関数を大きくする罰金項として作用している。

係数A, Bは正しい解を出力するように任意に選ぶことができる。
分割の方法
D-Waveマシンに当てはめられる完全グラフの最大の点の数は理論的には49個であるが、実際はおおよそ45個くらいである。そのため、それより大きいグラフは分割する必要がある。
まずグラフの一点vを定め、その一点の隣接する点の集合を$G_1$ (vは含まない)とv以外で構成される$G_2$と分けることができ、グラフGの最大クリークは($G_1$の最大クリークの数 + 1) or $G_2$の最大クリーク数である。 (B)

上の2つを用いて全ての部分グラフがDWに当てはめられるように分割してゆくアルゴリズムが以下である。

古典計算を用いた方法

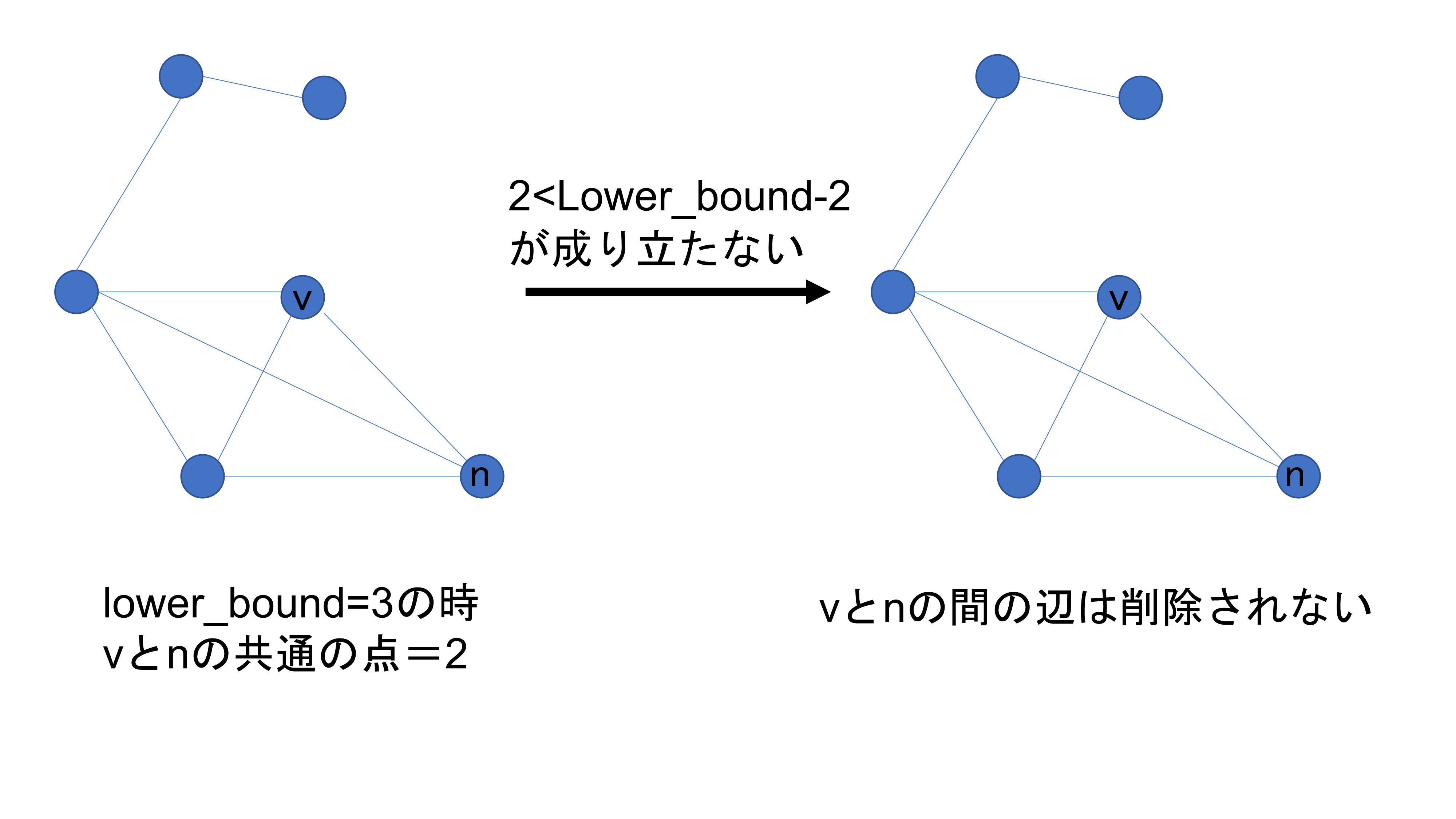
得られた部分グラフについて、最大独立集合(最大クリーク)を見つけるアルゴリズムは、求める集合に関係のない辺や点を消すアルゴリズムが用いられる。グラフG=(V, E)についてある関数を用いてk-core (点の次数kより小さいものを削除していき最終的にグラフが存在したものがk-core)の値の変数lower_boundを定める。グラフの任意の点vを決め、その隣接する点nに対してそれぞれ、共通する点の数<lower_bound-2が成り立つ時、vとnの間の辺を削除する。これを繰り返すことで最大クリークに関係ない辺や点を削除できる。
これらを全ての点に対して行うと最大クリークのグラフのみが残る。
D-Waveマシンを用いた方法
得られた部分グラフについて、前述のQUBO表現された目的関数を最小化するようにD-Wave 2Xを用いた。
結果
D-wave 2Xを用いて解いた結果、点の数が45個くらいでは古典的な方法 (fmc, pmcなど) の方が早いが、点の数が800個以上になるとD-Wave 2Xで解いた方が早いという結果が出た。現段階ではD-Waveマシンを用いて最大クリーク問題を解く利点はあまりないが、今後量子ビットの数が増えてゆけば古典的な方法よりも点の数に関わらず早く解を見つけられると考えられる。
本記事の作成者
神津岳志(編集:みやままさみち)