ナーススケジューリング問題をD-Wave 2000Qで解く

文献情報

タイトル: Application of Quantum Annealing to Nurse Scheduling Problem
著者: Kazuki Ikeda, Yuma Nakamura & Travis S.Humble
書誌情報: Scientific Reports 9, Article number: 12837 (2019) https://doi.org/10.1038/s41598-019-49172-3

概要

ナーススケジューリング問題とは

医療現場では人の命に関わる業務を行っているため、看護師の勤務の質が厳しく求められています。しかし、看護師の生活の質も守らなければいけないため、勤務表の作成が困難になっています[1]。ナーススケジューリング問題 (Nurse scheduling Problem, NSP)とは、複数の制約の下で看護師に最適なシフトを割り当てる問題です。NSPは1969年以前より研究されており、NP困難であることが知られています[2]。

問題

NSPでは様々な制約例が考えられます。例えば、こなせる仕事量 (労働力) は看護師の経験値に依存します。そのため、業務の多い日に新人のみで働くことは出来ません。よって、「各日に必要な労働力を確保する」制約が必要です。他にも多くの制約を考慮することもできますが、本論文では制約を以下の3つに定めています。

2日以上連続して勤務する看護師がいないようにする（ハード制約）
各日に必要な労働力を確保するようにする（ハード制約）
忙しさに応じて出勤回数を調整できるようにする（ソフト制約）

制約には、ハード制約とソフト制約があります。ハード制約は必ず満たさなければならない制約です。一方、ソフト制約は必ずしも満たす必要はないものの、満たすのが望ましい制約です。

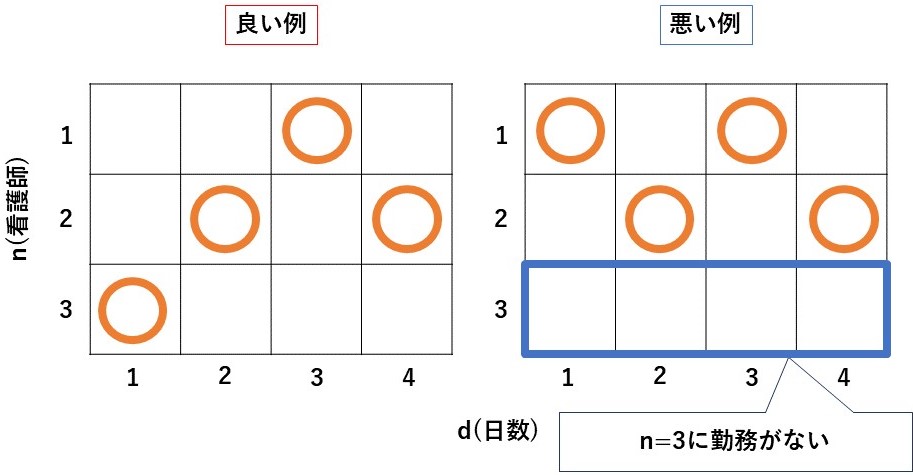
図1は、看護師3人で4日勤務する場合を計算したシフトスケジュールです。このように、NSPには複数のハード制約があるため従来の数値解法[3]では全ての制約を満たすのが困難です。
本論文ではNSPを組合せ最適化問題として捉え、QUBO形式に変換します。そして、D-Wave 2000Qで解くことにより、NSPに対する量子アニーリングの計算性能を検証します。

方法

QUBOへの変換

NSPを量子アニーリングで解くために、QUBO形式に変換します。

定数

看護師(Nurses)： n = 1,…,N
日数(Days):：d = 1,…,D
行列J：看護師nが2日以上連続で勤務するとペナルティを課す

$$
J_{i(n, d), j(n, d’)}
=
\left\{\begin{array}{cc}
a>0 & \text {if } |d – d’| = 1 \
0 & \text { otherwise }
\end{array}\right\}
$$

d日に必要な労働力： W(d)

看護師nの持つ労働力：E(n)

看護師nが希望する勤務日数：F(n)　※1

看護師nがd日に勤務希望する：G(n,d) ≔ h₁(n)h₂(d)　※2

※1 最低限の出勤回数を定めるためにF(n)に$ F(n) ≥ [D/N] $という条件を付けます。ここで、$ [x] ~ (x∈R) $ は$ x $ の整数部分の表します。
例えば、N=3,D=4では、F(n) ≥ 1となります。つまり、各看護師は4日間で1回以上は働かなければいけません。

※2 また、忙しさや時間帯によって出勤回数を調整するため、$ h_1 (n), h_2(n) $を次のように定義します。

$$
\begin{equation}
h_{1}(n):=\left\{\begin{array}{cc}
3 & \text { busy } \
2 & \text { moderate } \
1 & \text { idle }
\end{array}\right\} \quad h_{2}(d):=\left\{\begin{array}{cc}
2 & \text { weekend or night } \
1 & \text { weekday }
\end{array}\right\}
\end{equation}
$$

変数

・バイナリ変数: q_n,d∈ {0,1}
　q_n,d= 1は看護師nがd日に働くことを表します。

QUBO

全ての制約を満たすとき、値は0となります。

第1項の補足

第1項は、行列Jを使わずに第1項をシンプルに表現することもできます。

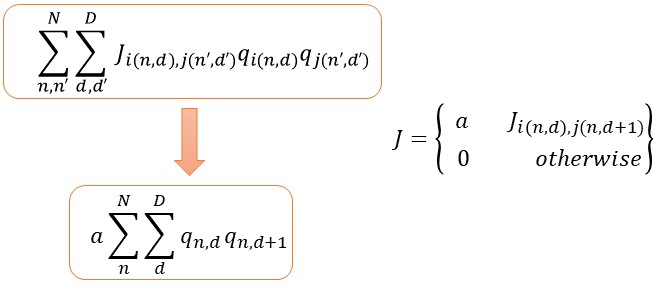
第3項の補足

第3項のh₁h₂について、具体例を元に理解を深めましょう。

N = 3、D = 4
h₁(1) = 1 (暇), h₁(2) = 2 (普通), h₁(3) = 3 (忙しい)
h₂(d) = 1 (常に平日）
F(n) = 4 (全員,毎日働きたい)

このとき、

n=1（暇な人）では,
$\left(\sum_{d}^{D} q_{i(1, d)}-4\right)^{2}$
→4回働くように最適化

n=2（普通の人）では,
$\left(\sum_{d}^{D} 2q_{i(2, d)}-4\right)^{2}$
→2回働くように最適化

n=3（忙しい人）では,
$\left(\sum_{d}^{D} 3q_{i(3, d)}-4\right)^{2}$
→4/3回働くように最適化

これより、暇な人ほど多く、忙しい人ほど少なくシフトが入るように最適化されることが分かります。

実験・結果

以上で定式化が終わりました。
いよいよ、D-Wave 2000Qを用いて実験します。設定は次の通りです。

定数
- N = 3 , 4 (看護師の人数)
- D = 5 – 14 (日数)
- λ = 0.3, γ = 1.3 (制約の係数)
- a = 7/2　 (2日以上勤務すると課されるペナルティ)
- h₁(n)= 1 　 (全員、暇)
- h₂(d)= 1　 (常に平日)
- E(n) = 1　 (全員が1人分の労働力を持つ)
- W(d) = 1　 (各日付dに1人分の労働力が必要)
D-Wave の設定
- アニーリング時間:　200μs
- サンプル数:　1000

QUBOに上の具体的な値を代入すると、第2項、第3項は次の意味に変わります。

[実験1]FA vs SA

フォワードアニーリング(FA)、シミュレーテッドアニーリング(SA)を用いて、基底状態を見つける確率を比較します。

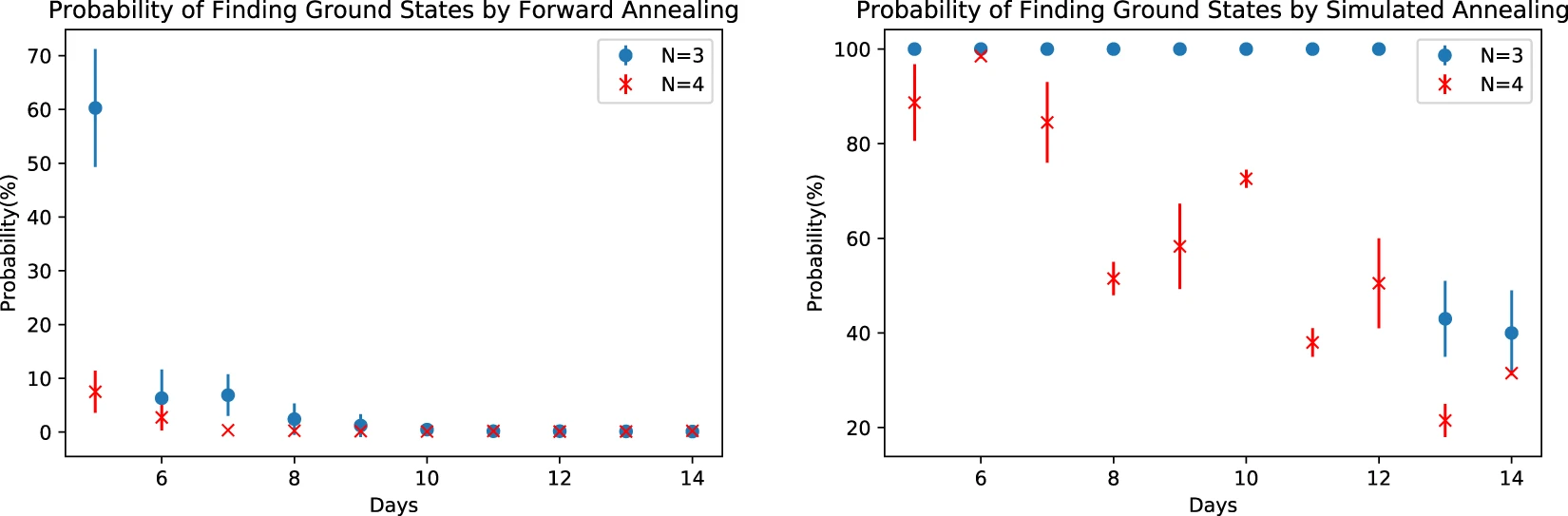
実験1_結果 — 図2: 基底状態を見つける確率(エラーバーは標準偏差) (https://doi.org/10.1038/s41598-019-49172-3)

FAでは、日数Dが大きくなると基底状態の解を1回も見つけられていません。一方、SAでは全ての場合で基底状態の解が観測されています。これより、SAの方が有用であると考えられます。

[実験2]FA vs RA

FAとリバースアニーリング(RA)を用いて、基底状態を見つける確率を比較します。
RAは、FAで得られた解を初期状態とします。そして、横磁場を切った状態から徐々に横磁場を印加し、再び横磁場を切るという操作によって、より良い解を探索します。本論文では、以下のように横磁場を調整しています。

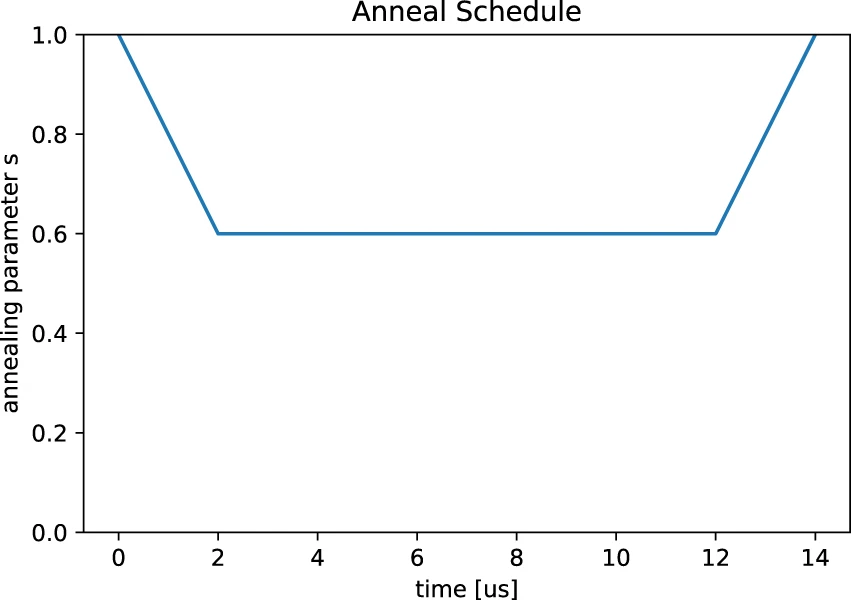
図3: アニーリングスケジュール (横磁場の強さをどのように変化させるのかを表します)(https://doi.org/10.1038/s41598-019-49172-3)

実験2では、RAの初期状態をFAの解からランダムに選んでいます。FAとRAによる基底状態を見つける確率を以下に示します。

図4: 基底状態を見つける確率(エラーバーは標準偏差) (https://doi.org/10.1038/s41598-019-49172-3)

RAにより、ほとんどの場合で解の改善に成功しています。一方、NとDを大きくすると、FAと同様に確率が0であることから、RAは必ずしもFAより精度を向上させないことも分かります。また、実験2では初期入力がランダムに選ばれているため、FAの解の分布に強く影響されます。なぜなら、FAの解には基底状態に近い解や、基底状態から遠い、質の悪い解も含まれているためです。これより、精度が向上するのは初期状態が基底状態に近い場合と考えられます。そこで、次の実験3では初期入力として基底状態に近い解を選んで精度を比較します。

[実験3]初期入力がランダム vs 初期入力が低エネルギー

RAの初期状態が基底状態に近い場合の、基底状態を見つける確率を求めます。初期状態は、FAで得た最もエネルギーの低い解を使用します。

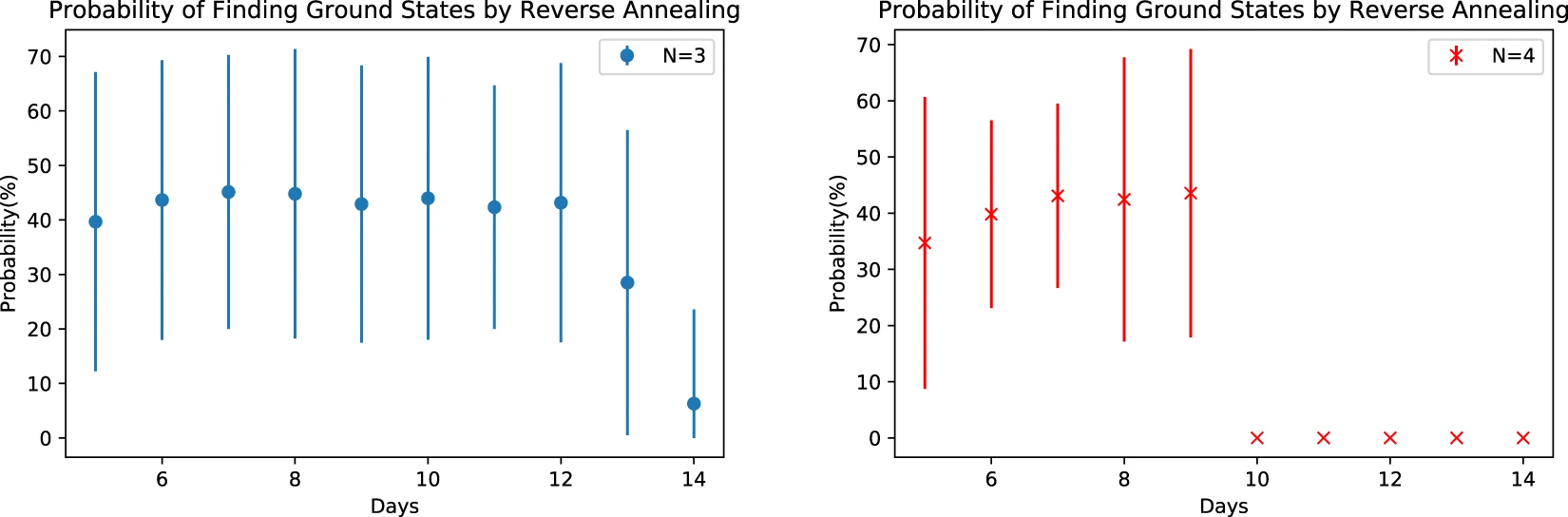
実験3の結果 — 図5: 基底状態を見つける確率(エラーバーは標準偏差) (https://doi.org/10.1038/s41598-019-49172-3)

初期入力がランダムだった時よりも精度は向上しています。とはいえ、基底状態を使っても同じ基底状態が得られるとは限りませんでした。これは、横磁場の調整度合いによって極小解に陥ってしまう可能性を示しています。

結論

NSPを解くには、FAよりもSAを用いた方が有効だと分かりました。しかし、FAで得た解はRAによって改善することが可能でした。さらに、RAの初期入力を基底状態に近い解とすることで、より基底状態を見つける確率が高くなりました。

編集者あとがき

SAの結果がFAよりもかなり良くて残念でした。制約項の係数を調整することで、本論文よりも良い結果が得られるか検証したいと考えています。また、結果が同じグラフにプロットされていないため比較が難しかったです。加えて、W(d)やG(n,d)といった変数を1以外で置いた結果も気になりました。そこで、今後再現実験を行い、結果を別の記事「ナーススケジューリング問題をD-Wave 2000Qで解く (検証編)」で紹介していますので、ぜひ読んでください。

参考文献

[1]池上敦子,(9 June 2005).”ナース･スケジューリング-調査･モデル化･アルゴリズム-”
[2]Solos, Ioannis; Tassopoulos, Ioannis; Beligiannis, Grigorios (21 May 2013). “A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem”. Algorithms. 6 (2): 278–308.doi:10.3390/a6020278.
[3]Cooper, T. B. & Kingston, J. H. The complexity of timetable construction problems, In International Conference on the Practice and Theory of Automated Timetabling, pp. 281–295 (Springer, 1995).

本記事の担当者

鹿内怜央 (メンタリング：丸山尚貴、羽場廉一郎)

Post Views: 487