文献情報
タイトル : Graph Partitioning using Quantum Annealing on the D-Wave System
著者 : Hayato Ushijima-Mwesigwa, Christian F. A. Negre, and Susan M. Mniszewski
書誌情報:https://arxiv.org/abs/1705.03082
まえがき
本論文は既にジャーナル版も公開されている。最新情報に関してはそちらを参照されたい。(https://doi.org/10.1371/journal.pone.0227538)
本記事で登場する、「グラフ分割問題」や「ラプラシアンマトリックス」等の意味についての詳細な説明は本記事の最後の方にある語彙補足集に、あくまで筆者が勉強した補足として書いているため参考にしていただきたい。
概要
本論文では、グラフ分割問題を取り扱う。グラフ分割問題とはグラフのノードを複数のグループに分割することであり、以下の二つの条件を満たすことを考える。
- カットする辺の数を最小にする
- 各グループのノード数ができるだけ等しくなるようにする
今回はグラフ分割問題を分割数が2の場合はグラフの最小カットとして、分割数がkの場合はCommunity Detection (CD) として、それぞれコスト関数を定義する。
これらのコスト関数は、D-Wave Systems の量子アニーリングマシンを用いてヒューリスティックに解くことが可能である。コスト関数の変数間の結合は完全グラフの形状をとる一方、D-Wave マシンの量子ビット間の結合はスパースである。そのため、論文公開当時の最新機種であるD-Wave 2Xに実装可能な任意の問題の変数は高々45個と少なく、実際の大きな問題に対しては非現実的である。したがって、本論文では実装を工夫することで、さらに多くのノード数を持つようなグラフ分割問題をD-Wave マシンを用いて解くことを考える。具体的には、グラフの辺数を削減するために、辺重みに対するしきい値(Threshold)を導入する。
また、使用する量子ビットの数は、グラフのノード数と分割数に比例して増加する。したがって、量子アニーリングで全て計算しようとすると量子ビットが足りなくなってしまうため、D-Wave マシンと古典コンピュータのハイブリッド方式でこの問題に取り掛かる。
方法
量子アニーリングでグラフ分割問題を解くために、コスト関数の最小化問題として定義する必要がある。本論文では、分割数が2の場合と3以上の場合に分けて定式化を行う。
分割数が2の場合
ノードの隣接関係について、各ノード間の重みを行列として以下のように定義する。
\begin{equation}
A_{ij} =
\left \{\begin{array}
{l}0 (i=j のとき) \\
W_{ij} (i\neq j のとき)
\end{array}\right.
\end{equation}
ただし、$W_{ij}$は辺$ij$の重みを表す。$W_{ij} = 0$である場合には辺ij が存在しないことを表している (図1参照)。
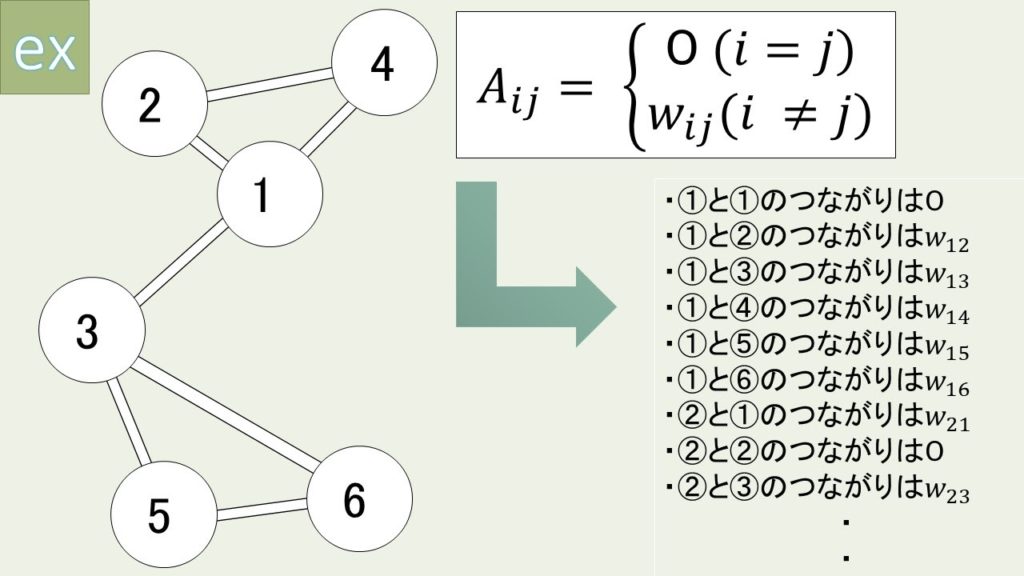
次に、「一つの点に対して、どのくらいの点が隣接しているか、また、どれだけの重みがあるのか」を表す定数を次式のように定義する (図2参照)。
$$g_i = \displaystyle\sum_{j}^{} A_{ij}$$
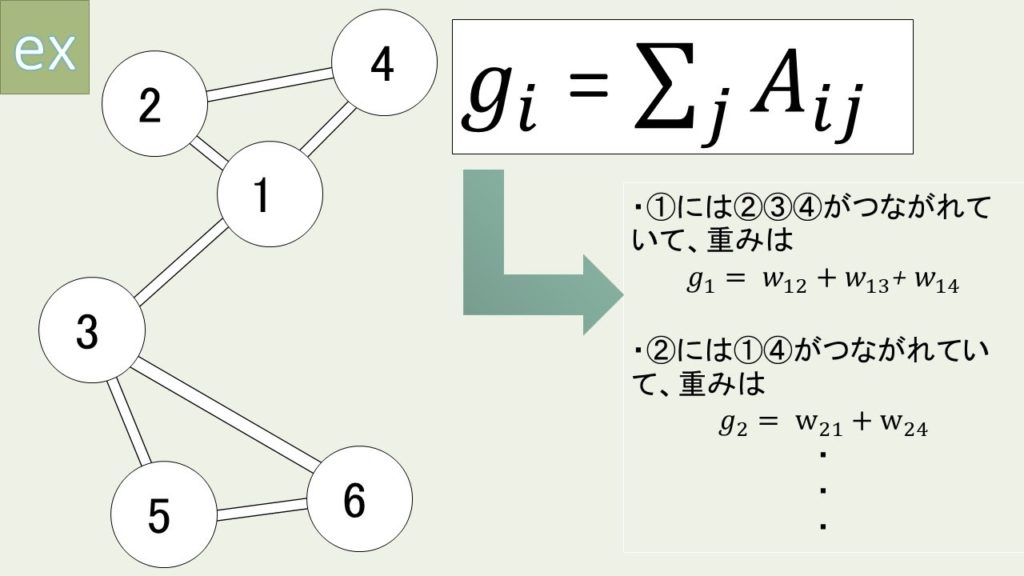
すると、モジュラリティは次式のように定義される。モジュラリティはグラフ分割問題において、広く用いられる手法である。
$$B = A – \frac{gg^t}{2m}$$
$$B_{ij} = A_{ij} – \frac{g_ig_j}{2m} = A_{ij} – \frac{g_ig_j}{\sum_{i}^{}g_i}$$
続いて、分割した際にノードがどのグループに属すかを表す二値変数を定義する。2つのグループは片方を+1、もう片方を-1とすることで区別が可能となる (図3参照)。
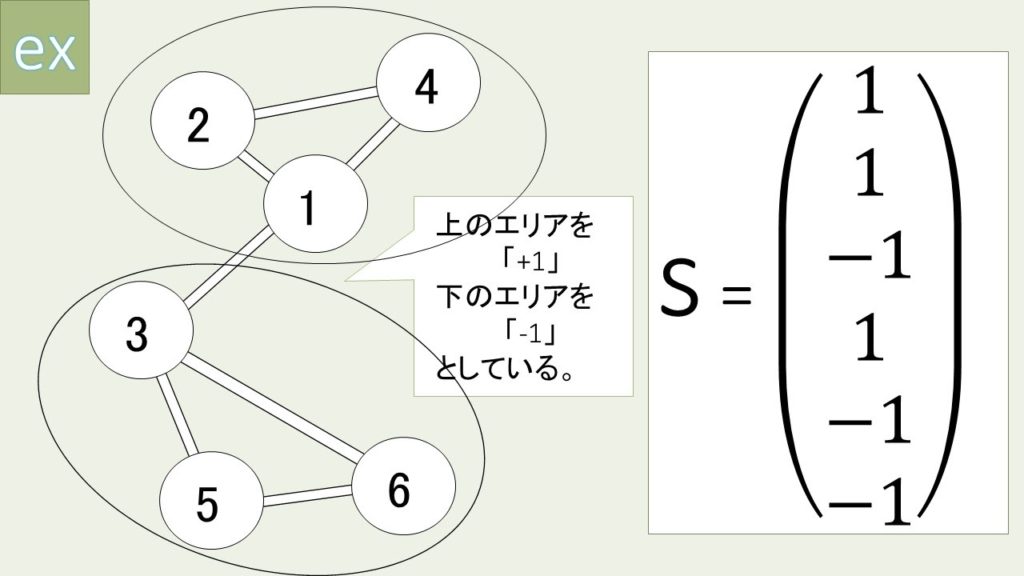
最終的に、以下のように最小化したいコスト関数Q(s)を定義する。
$$Q(s) = s^TBs$$
$Q (s) $を最小化問題はイジング模型の形式となっており、D-Waveマシンで実行可能な形式となっている。
分割数がkの場合
今回定式化するコスト関数は目的関数項と制約項から成り立っている。以下にそれぞれについて説明する。
コスト関数の目的関数項について
まず、ノードがどのグループに属すかを表す二値変数を定義する。今回は分割数が2のときと違い、±1だけでは表現できない。そのためn(ノード数)×k(分割数)の行列を用いて次式のように表す (図4)。
\begin{equation}x_{ij} = \left \{\begin{array}{l}1(ノードiがj番目のグループにあるとき) \\0 (上記以外)\end{array}\right.\end{equation}
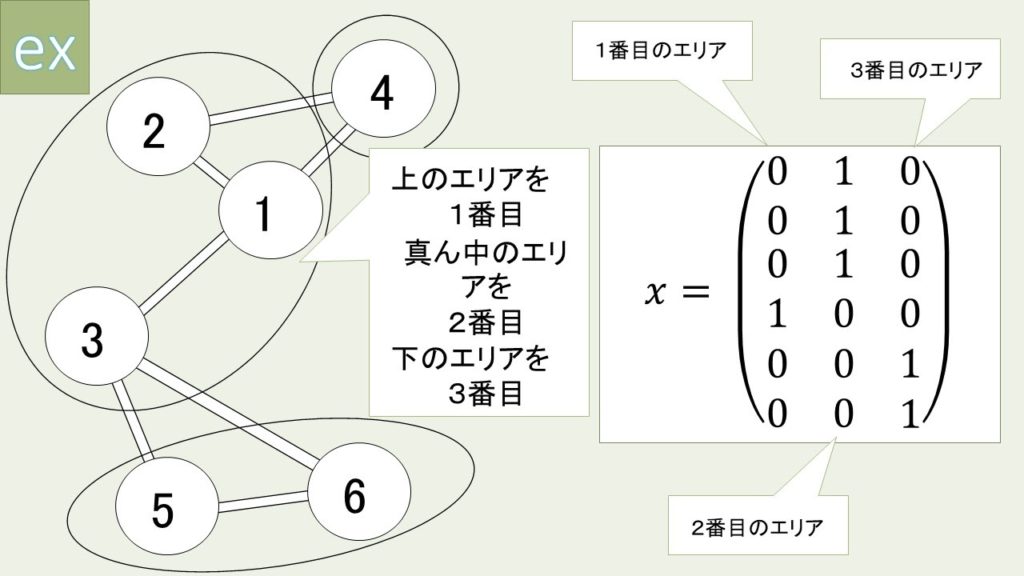
$$\sum_{j=1}^{k} x_j^T L x_j$$
ここで、$x_j$ は行列$x$の$j$番目の列ベクトルである。この目的関数項の値はカットする辺の数に比例するため、この値が小さいほど良い分割となる。
コスト関数の制約項について
まず、各ノードが必ずただ一つのグループに属するように制限するような制約項を導入する。すなわち、ここで課す制約は、任意の$i $について、以下の等式が成立するというものである。
\begin{equation}
\sum_{j=1}^{k}x_{ij} = 1
\end{equation}
これを制約項として緩和することでコスト関数に組み込む。コスト関数のメインの項の値は、カットする辺の数に比例した値をとる。そのため制約項は違反すると値が大きくなってしまうように以下のように設定すればよい。
\begin{equation}
(制約項①) = \sum_{i=1}^{n} γ_i \left(\sum_{i=1}^{k}x_{ij} – 1\right)^2
\end{equation}
ただしγは制約項の強さを表す定数である。
次に、ノードができるだけ均等に分かれるように制限する制約項を導入する。そのためには、n個のノードをk個のグループに分割した時、各グループのノード数をn/kに近づけるような次式のような制約項を設ければよい。
\begin{equation}
(制約項②) = \sum_{j=1}^{k} α_j \left(\sum_{i=1}^{n} x_{ij} – \frac{n}{k}\right)^2
\end{equation}
ただし、αは制約項の強さを調整する定数である。
求めたいコスト関数
以上により、コスト関数Q'(x)は以下のように定義できる。
\begin{equation}
Q'(\mathbf{x}) = β\left( \sum_{j=1}^{k}x^T_jLx_j \right)+ \sum_{i=1}^{n} γ_i \left( \sum_{i=1}^{k}x_{ij} – 1 \right) ^2 \sum_{j=1}^{k} α_j \left(\sum_{i=1}^{n} x_{ij} – \frac{n}{k} \right) ^ 2
\end{equation}
コスト関数Q'(x)の最小化は、QUBO (Quadratic Unconstrained Binary Optimization) と呼ばれ、D-Waveマシンで実装可能な問題である。
しきい値を使った辺の削減
D-Wave マシンにコスト関数を実装する際には、コスト関数の変数間の隣接関係 (辺) を実機のプロセッサ上のグラフ構造に割り当てる必要がある。この際、マイナー埋め込みという手法を用いられる。マイナー埋め込みでは、1個の二値変数を複数の量子ビットを用いて表現する。したがって、今回のコスト関数中の定数B, Lによっては、多くの量子ビットを消費してしまうという問題があるのだ。
本論文では、BまたはLに対してしきい値を導入することで、グラフ分割の精度を極力落とさずに変数間の辺の数を減らす。例えば、しきい値が0.12のとき、0<Bij(もしくはL)<0.12のBij(もしくはL)を0として扱う。
表1に分割数が2の場合にしきい値を導入した場合の結果を示す。しきい値の値に連動して、モジュラリティが減ってしまう代わりに、コスト関数の変数間の辺数が少なくなっていることが分かる。

また、表2は分割数が4の場合にしきい値を導入した場合の結果を示す。

表1、表2のいずれの結果においても、コスト関数の変数間の辺数が減り、D-Wave マシンに埋め込む際に要求される量子ビット数を減らすことができている。
結果
分割数が2の場合において、二つのデータセットを用いて提案手法と既存手法(METISやKaHIP)を比較する。
D-Waveを用いる際には、小さな問題に対して問題全体を実機で計算する場合と、大きな問題に対して分割して複数回計算を行う場合に使い分ける。今回は前者をsapiと呼び、後者をqbsolvと呼ぶことにする。
1つ目のデータセットには最大70の頂点を持つ比較的小さいグラフが含まれている。2つ目のデータセットは最大9000個の頂点を持つグラフから構成されている。
結果を表3に示す。

最初のデータセットのグラフについて、前述した通り、D-Wave 2Xマシンによりグラフ分割できるノード数の限界は45であるが、今回の検証のQUBO定式化によりノード数が45以上のものについても取り扱うことができている。
次に、二つ目のデータセットでは、D-Waveマシンにはqbsolvを使用してグラフ分割を行った。すべての処理を量子アニーリングで行わず、古典コンピュータとのハイブリッド方式で行うことにより、ノード数が100を超えるグラフの分割が可能となった。その分割の結果を以下の表4に示す。表1同様、値はカットする辺の数である。また、使用したグラフは(Chris Walshaw :: Research :: Partition Archive)から閲覧することができる。

続いて、ノード数がN、分割数がk=2×n(nは自然数)の場合について、様々なグラフに対して実験を行った。表5、表6に結果を示す。


最後に分子の電子構造グラフに対して実験を行う。表7は、二つの分子において、分割数を変更した場合の結果である。Pheny dendrimerの場合はqbsolvを用いた場合の結果の方が従来の結果よりカット数が増加してしまっているが、Peptide laftの場合はカット数に置いてより良い結果を残すことができている。

結論
今回実験した、量子アニーリングと古典コンピュータを併用して行ったグラフ分割の結果は、これまでのグラフ分割の方法(METISやKaHIP)と同等、もしくはそれ以上の結果を残すこととなった。
また、モジュラリティとしきい値を利用することにより、分割の質に対する影響を抑えながら、量子ビット数を減らし、グラフ分割を実行することができた。
語彙と補足
この語彙補足集はこの記事のライターが書いたものであり、論文に書かれていた解釈とずれている可能性があることを考慮して欲しい。
グラフ
グラフとは、点(ノード)と辺(エッジ)からなる組のことである。その特徴は、点同士のつながりのみに着目しているという点である。すなわち、点同士のつながり方さえ同じであれば、点の位置はどこでもよいということである。
グラフ分割問題
グラフ分割問題には以下の2種類がある。
・カットする辺の数(重み)を最小にする方法
・モジュラリティによる分割
ラプラシアンマトリックスとコスト関数のメイン項の求め方
以下の説明は以下のURLから閲覧できる『グラフラプラシアンを噛み砕いて噛み砕いて跡形もなくしてみた』(https://qiita.com/silva0215/items/0d1d25ef51b6865a6e15)という記事を参考にしている。
ラプラシアンマトリックスは、隣接行列Dと次数行列Aを用いて、以下のように定義されている。
$ L = D – A $
以下のグラフを例に解説する。
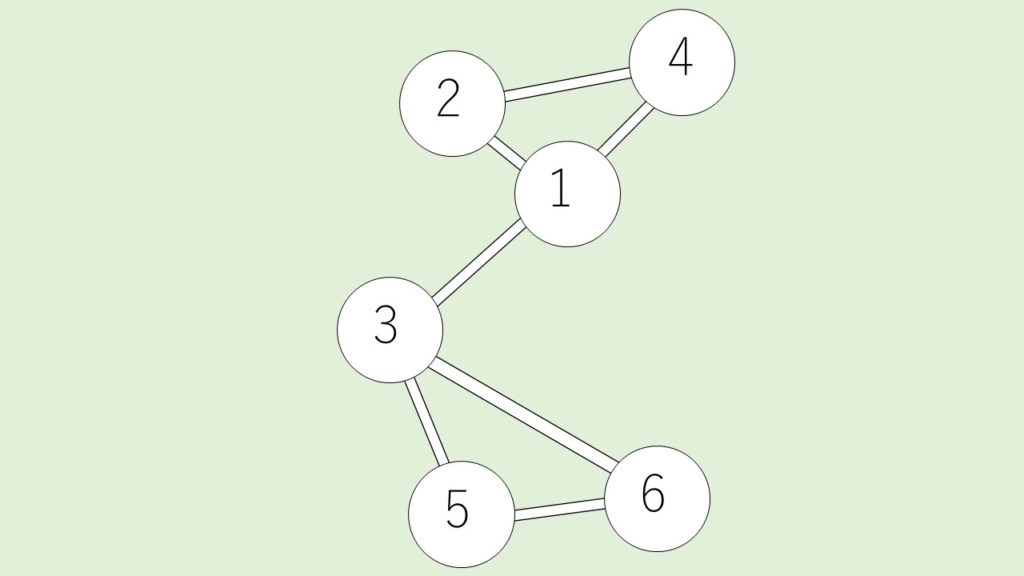
隣接行列について
D(隣接行列)とは、行も列も頂点に対応しており、頂点iと頂点jがつながっている場合は1、頂点iと頂点jがつながっていない場合は0となる。例えば、頂点1と頂点2とが辺でつながっているとき、1行目2列目は1となる。さらに2行目1列目も1となる。よって、隣接行列は必ず対称行列となる。
例に挙げたグラフでは、隣接行列Dは以下のようになる。
$$
D = \begin{pmatrix}
0&1&1&1&0&0 \\
1&0&0&1&0&0 \\
1&0&0&0&1&1 \\
1&1&0&0&0&0 \\
0&0&1&0&0&1 \\
0&0&1&0&1&0
\end{pmatrix}
$$
次数行列について
A(次数行列)も、行も列も頂点に対応しており、頂点に接続する辺の数を表している。すなわち、i行目i列目に頂点iから出ている辺の数が対応している。すなわち、次数行列は対角行列である。
例に挙げたグラフでは、次数行列Aは以下のようになる。
$$
A = \begin{pmatrix}
3&0&0&0&0&0 \\
0&2&0&0&0&0 \\
0&0&3&0&0&0 \\
0&0&0&2&0&0 \\
0&0&0&0&2&0 \\
0&0&0&0&0&2
\end{pmatrix}
$$
ラプラシアンマトリックスの計算
前述したように、ラプラシアンマトリックスの定義はL=D-Aであるから、例におけるラプラシアンマトリックスは以下のようになる。
$$
L = \begin{pmatrix}
3&-1&-1&-1&0&0 \\
-1&2&0&-1&0&0 \\
-1&0&3&0&-1&-1 \\
-1&-1&0&2&0&0 \\
0&0&-1&0&2&-1 \\
0&0&-1&0&-1&2
\end{pmatrix}
$$
ラプラシアンマトリックスの別の求め方
また、ラプラシアンマトリックスには、別の求め方がある。頂点iから頂点jの向きで辺がつながっているときは1、逆向きでは-1とする行列Cを定義する。まず、具体例のグラフの辺の向きを任意に決定する。
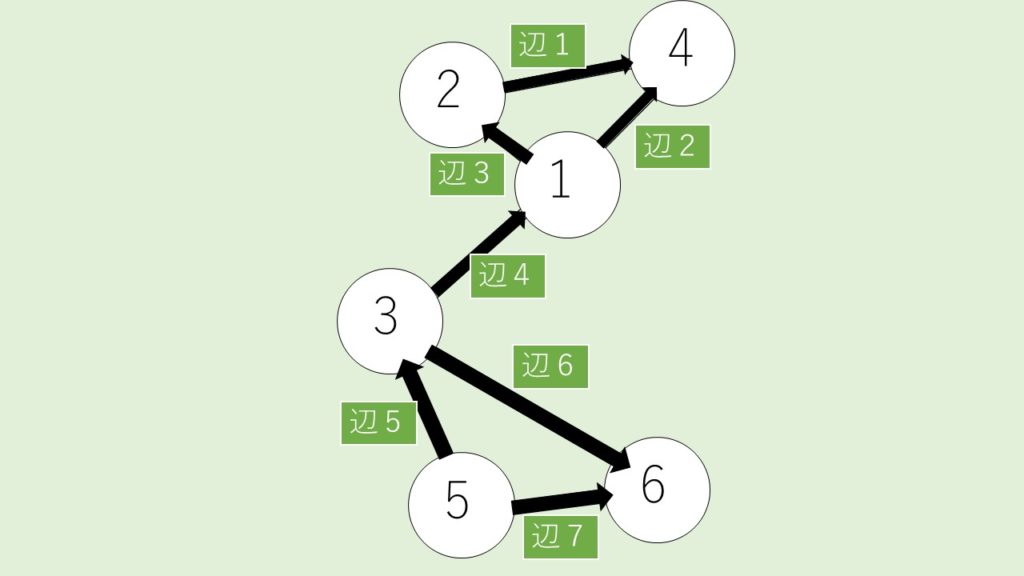
このとき、行列Cは以下のようになる。
$$
C = \begin{pmatrix}
0&1&1&-1&0&0&0 \\
1&0&-1&0&0&0&0 \\
0&0&0&1&-1&1&0 \\
-1&-1&0&0&0&0&0 \\
0&0&0&0&1&0&1 \\
0&0&0&0&0&-1&-1
\end{pmatrix}
$$
すると、ラプラシアンマトリックスLはCとCの転置行列の積で求められる。
$$L = C C^T$$
コスト関数のメインの項を求める。ここで、sは、各ノードがどのグループに属しているかを表している。すなわち、片方のエリアにある場合は1、反対側のエリアにある際は-1に対応しているのである。
まず分割数が2の場合におけるメイン項の導出について、以下の式を考える。
$$N_c = \frac{1}{4} \sum_{(i,j) \in E}^{} (s_i – s_j)^2$$
この式について、添え字i,jはいずれもノードに対応している。すなわち、ノードiとノードjが同じグループに分割されているときは、
$${1 – 1}2 or {(-1) – (-1)}2 = 0$$
ノードiとノードjがそれぞれ別のグループに分割されていた時は、
$${1 – (-1)}2 or {(-1) – 1}2 = 4$$
これをすべてのノード間について計算しているため、右辺のΣ以降は、カットする辺の数の4倍の値となっていることが分かる。
確かに$N_c$はカットする辺の数のとなっていることが分かる。
次に、以下の式について考える。
$$\| s^T C \|^2$$
$s^T C$は、(1×n行列)×(n×n行列)より、(1×n行列)となる。そしてこの行列の各列の値は、ある辺が分割されているかを判定できており、分割されていない場合は0,分割されている場合は、2となっている。したがってこれを2乗したときの値は4でありその総和であるため、$\| s^T C \|^2$もカットする辺の数の4倍を表している。
$s^T C$は各辺がカットされているかいないかの指標を表すこととなっている。
ゆえに、以下の等式が成り立つ。
$$\sum_{(i,j) \in E}^{} (s_i – s_j)^2 = || s^TC ||^2$$
したがって、カットする辺の数を最小にすることが目標であるため、カットする辺の数の4倍を表す$|| s^TC ||^2$が最小となる場合を求めればよい。
ここで、$|| s^TC ||^2$についてさらに変形する。まず、
$$|| s^TC || = ||C^Ts||$$
であるから、
$$|| s^TC ||^2 = s^TCC^Ts$$
とできる。ここで、ラプラシアンマトリックスは
$$L = CC^T$$
であることから、最終的に
$$N_c = \frac{1}{4} (s^TLs)$$
となり、コスト関数のメインの項を導くことができた。
分割数がkの場合もこれと同様にして導くことができる。
感想&あとがき
今回この記事を書きました、日髙です。工学部の1年生で初めて英語の論文なるものを読み、分からないことだらけで本当に時間がかかってしまいました。(本当につらかったです・・・)
僕が本当に苦労したのは以下のことで、
- 英単語が分からないのが多すぎる
- 「グラフ」が何か全く分からなかった
- グラフ分割に2種類も方法があったこと
- ラプラシアンマトリックス・モジュラリティ
- コスト関数のメイン項がいきなり$s^TLs$で定義されていたこと
軽い気持ちでこのt-waveのバイトに参加してしまったことを少し後悔したことは苦い思い出です。研究っていうのは好きだからこそできるんだと身をもって、1年生の時点で体験できたことは本当に幸運だったと思います。さらに幸運なことに、本論文を通して、僕はグラフや量子アニーリングに興味を持つことができたので、苦しみながら今後も励んでいこうと思います!
本記事の担当者
日高光稀 (メンタリング:丸山尚貴、羽場廉一郎)