概要
記事「量子アニーリングを用いたグラフ彩色」では貪欲法によるグラフ彩色の際に、サブルーチンとして独立点集合を量子アニーリングで求めた場合と古典コンピュータで求めた場合において、グラフ彩色の最適化性能を比較しました。本記事では古典コンピュータで独立点集合を求める3つの近似的なアルゴリズムRamsey、CliqueRemoval、SampleISを説明します。
最大独立点集合とクリーク
独立点集合とはどの2頂点においても結ぶ辺が存在しない頂点集合のことです。グラフ彩色の貪欲法では独立点集合を求めて1色ずつ割り当てることを繰り返します。この貪欲法ではすべての頂点に色を割り当てるまでの繰り返しの回数が彩色の色数となるので求める独立点集合は頂点数の多い方が色数が小さくなることが期待できます。なお常に最大独立点集合を求めても最小色数の彩色が得られるとは限りません。例えば以下のグラフでは最小色数は3色ですが、貪欲法の各ステップで最大独立点集合を常に求めると4色での彩色となります。
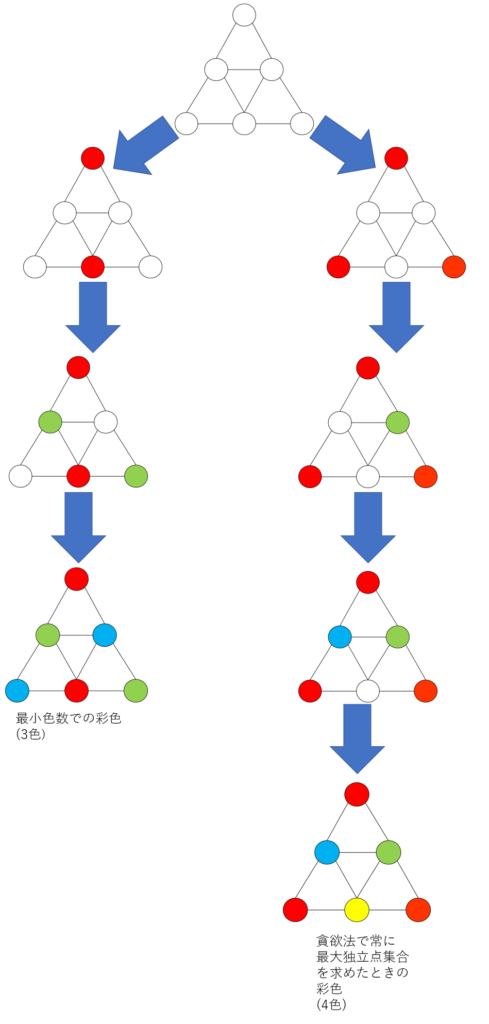
クリークとはどの2頂点においても結ぶ辺が存在する頂点集合のことです。グラフに頂点数$ k$のクリークが存在すると彩色に必要な色数は$ k $以上となります。例えば図1の例ではグラフに頂点数3のクリークが存在するので彩色には3色以上必要となります。
アルゴリズム
Ramsey
1つ目のアルゴリズムはRamsey[1]です。これは独立点集合とクリークをそれぞれ一つずつ求めるアルゴリズムです。Ramseyは頂点を一つ選び、その頂点に隣接している頂点の集合と、隣接していない頂点の集合とでそれぞれ再帰的に独立点集合とクリークを求めます。具体的には以下の通りです。ここで$ I$と$ C$はそれぞれ求める独立点集合とクリークを表します。
- グラフの頂点数が0ならば$ I=∅$、$ C=∅$として終了する。
- 頂点$ v$を選択する。
- 頂点$ v$に隣接している頂点の部分グラフでRamseyを実行し,独立点集合($ I_1$)とクリーク($ C_1$)を求める。
- 頂点$ v$に隣接していない頂点の部分グラフでRamseyを実行し,独立点集合($ I_2$)とクリーク($ C_2$)を求める。
- $ C_1$と$ I_2$に$ v$を追加する。
- $ I_1$と$ I_2$の頂点数が多い方を$ I$、$ C_1$と$ C_2$の頂点数が多い方を$ C$として$ I$と$ C$を求めて終了する。
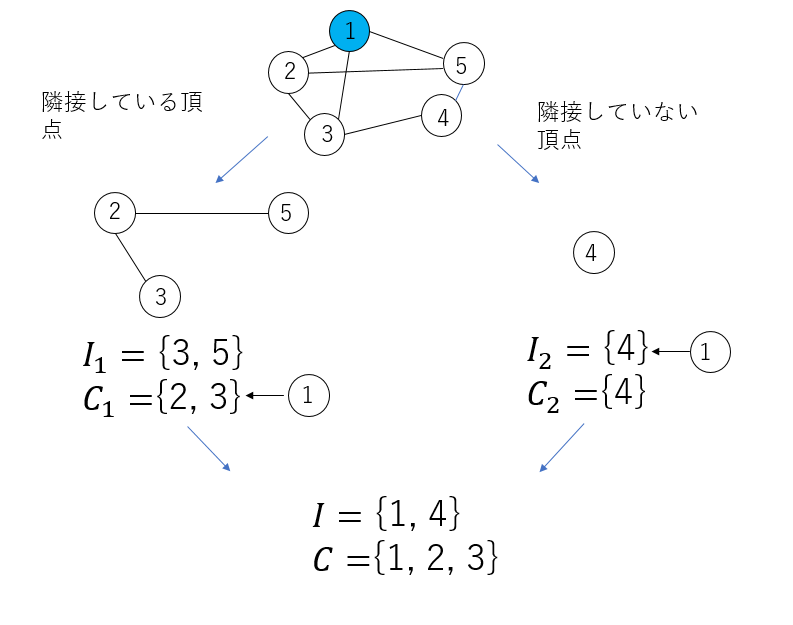
Ramseyは下図のように動作します。
CliqueRemoval
CliqueRemoval[1]はRamseyを改良したアルゴリズムです。これは独立点集合とクリークの集合を求めるアルゴリズムです。ただしRamseyとは異なり、CliqueRemovalでは複数個のクリークを求めます。CliqueRemovalはRamseyを実行してグラフからRamseyで得られたクリークを削除することを繰り返します。具体的には以下の通りです。ここで$ I$と$ C$はそれぞれ求める独立点集合とクリークの集合を表します。
- グラフからRamseyを利用してクリークと独立点集合を求める
- グラフから得られたクリークを削除する。
- グラフの頂点数が0ならば手順5へ移動する。
- Ramseyを利用してクリークと独立点集合を求めて手順2に戻る。
- 得られた独立点集合のうち、最も頂点数の多いものを$ I$とし、$ C$をすべての得られたクリークからなる集合として$ I$と$ C$を出力する。
CliqueRemovalは下図のように動作します。

SampleIS
SampleIS[2]は独立点集合を求めるアルゴリズムで、CliqueRemovalを改良したアルゴリズムです。SampleISは頂点数に応じて再帰的な実行またはCliqueRemovalの実行を行います。具体的には以下の通りです。ここで$ I$は求める独立点集合、$ n$はグラフの頂点数、$ k$はグラフを彩色する色の数を表し、グラフが$ k$色で彩色可能であると仮定しています。
- グラフの頂点数が1ならば$ I$にその頂点を追加して終了する。
- グラフから$ \log_{k}n$個の頂点をランダムに選択する(この頂点の集合を$ I_1$とする)。
- $ I_1$が独立点集合でないなら2.に戻る。
- $ I_1$のどの頂点にも隣接していないような頂点の数が$ \frac{n}{k}\log n / 2 \log \log n$以上ならば、$ I_1$に隣接していない頂点集合でSampleISを実行して独立点集合を求める。$ I$をSampleISで求めた独立点集合と$ I_1$の和集合を$ I$として終了する。
- $ I_1$に隣接していない頂点でCliqueRemovalを実行して独立点集合を求める。$ I_2$を求めた独立点集合と$ I_1$の和集合とする。
- $ I_2$の頂点の数が$ \log^{3}n/6 \log \log n$以上ならば$I= I_2$として終了する。
- 2.に戻る
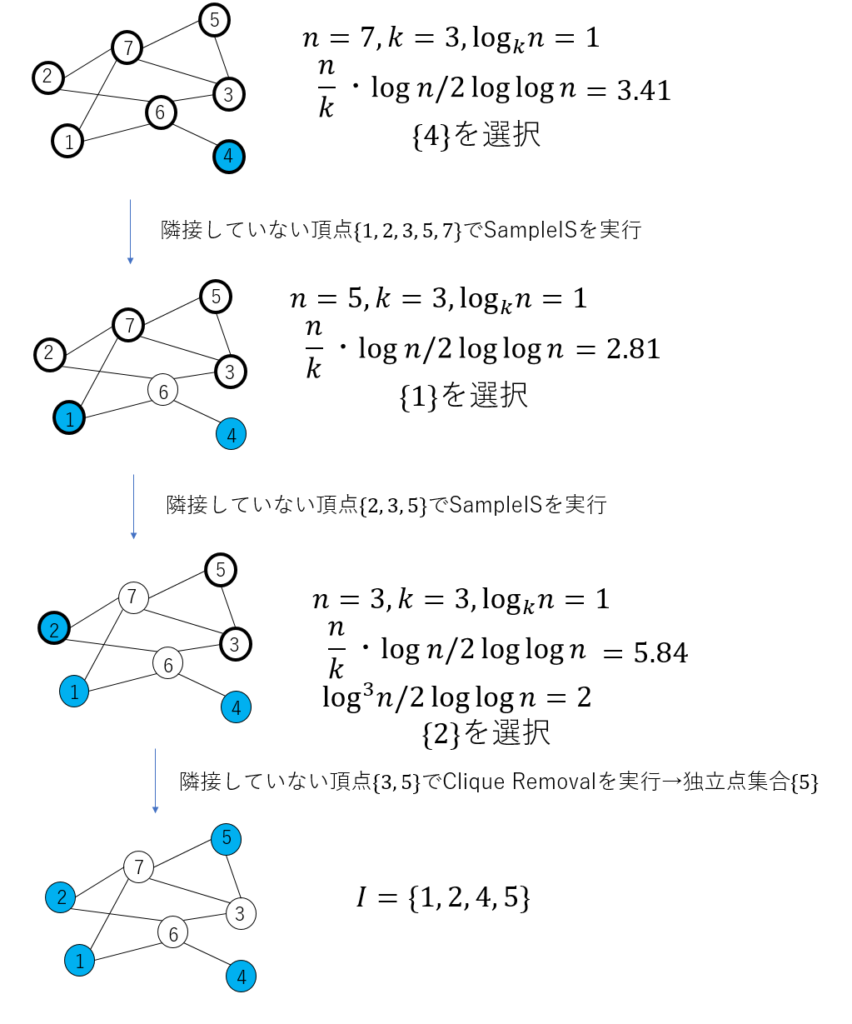
SampleISは下図のように動作します。
参考文献
[1] R.Bopanna and M.M.Halldórsson. Approximating maximum independent sets by excluding subgraphs. BIT Numerical Mathematics, 32(2), pp. 180—196, 1992.
[2] M.M.Halldórsson. A still better performance guarantee for approximate graph coloring. Information Processing Letters, 45(1), pp. 19—23, 1993.
あとがき
RamseyやCliqueRemovalは比較的単純に感じましたが、SampleISは頂点数などの基準で何を実行するかを決定するのが面白く感じました。これらのアルゴリズムの近似性能は理解できていないので勉強したいと思います。