文献情報

タイトル：Quantum annealing for combinatorial clustering
著者：Vaibhaw Kumar, Gideon Bass, Casey Tomlin, Joseph Dulny III
書誌情報：https://arxiv.org/abs/1708.05753

概要

クラスタリングとは、教師無し学習の一つで、類似した特徴を持ったデータが同じグループに属するようにグループ分けすることを指します。主な手法にk-meansや階層型クラスタリングがありますが、これらは局所探索法であるため最適解に到達する保証がありません。一方で、SAや遺伝的アルゴリズムのような大域的な探索手法では実行時間が長くなってしまいます。
そこで、本論文では高速に実行可能な量子アニーリングを利用します。まず、量子アニーリングマシンで計算可能な形でクラスタリングを定式化します。そして、その最適化を実行し得られた結果をk-meansと比較し、提案手法の利点と欠点について議論します。

今回紹介する定式化手法

本論文では、One-hot encodingとBinary clusteringの2つの定式化手法を紹介します。

従来のクラスタリングの定式化

クラスタリングは次のコスト関数$H$ の最小化として表現されます。

$$
H =
\frac{1}{2} \sum^K_{a=1} \sum_{C(i)=C_a} \sum_{C(j)=C_a} d(x_i,x_j) \tag{1}
$$

$x_i$は各データ点、$d(x_i,x_{j})$はデータ点間の距離です。また、$C(i)=C_a$は$i$番目のデータ点がクラスター$C_a$に属することを表します。つまり、このコスト関数$H$は同じクラスターに属するデータ点間の距離の総和となっています。

One-hot encodingの定式化

ここでは、$N$個のデータ点$x_i(i=1 \sim N)$を$K$個のクラスター$C_a(a=1 \sim K)$に割り当てるという問題を考えます。
まず、データ点$x_i$がクラスター$C_a$に属するかどうかを表現する二値変数$q_{i,a}$を以下のように定義します。

$$
q_{i,a} =
\begin{cases}
1 & \text{if データ点x_iがクラスターC_aに属する} \\
0 & \text{otherwize}
\end{cases}
\tag{2}
$$

この表現方法をOne-hot encodingと呼び、$q_{i,a}$によりコスト関数$H$は以下のように書き直されます。

$$
H’ = \frac{1}{2}\sum^N_{i,j=1}d(x_i,x_j)\sum^K_{a=1}q_{i,a}q_{j,a} \tag{3}
$$

しかし、このコスト関数を最小化するとすべての$q$が0、すなわち全てのデータ点がどのクラスターにも含まれない状態が最適解となってしまい、クラスタリングが実現できません。そこで、各データ点がただ1つのクラスターに含まれるように以下の制約$\Phi_i$を加えます。

$$
\Phi_i = \left(\sum^K_{a=1}q_{i,a}-1\right)^2 \tag{4}
$$

最終的にこの問題は以下のコスト関数$H$で定式化されます。

$$
H = H’ + \sum^N_{i=1}\lambda_i \Phi_i = \frac{1}{2}\sum^N_{i,j=1}d(x_i,x_j)\sum^K_{a=1}q_{i,a}q_{j,a} + \sum^N_{i=1}\lambda_i\left(\sum^K_{a=1}q_{i,a}-1\right)^2 \tag{5}
$$

ここで、$\lambda_i$は制約の強さを決める係数であり、制約違反を起こさないように十分大きくする必要があります。この十分な値を調べるために、ある1つのデータ点がどのクラスターにも割り当てられない場合に最大でどのくらいコスト関数$H’$の値が小さくなるかを考えます。
もし、各クラスターに最低1つはデータ点が割り当てられるとすると、1つのクラスターに含まれるデータ点の個数は最大で$(N-K+1)$個になります。この時、ある1つのデータ点がどのクラスターにも割り当てられなくなる（値が0になる）と、自身を除いた$(N-K)$個のデータ点との間の距離がコスト関数$H’$において足し合わされなくなります。図1では$N=6,K=3$のケースを例にこれを説明しています。

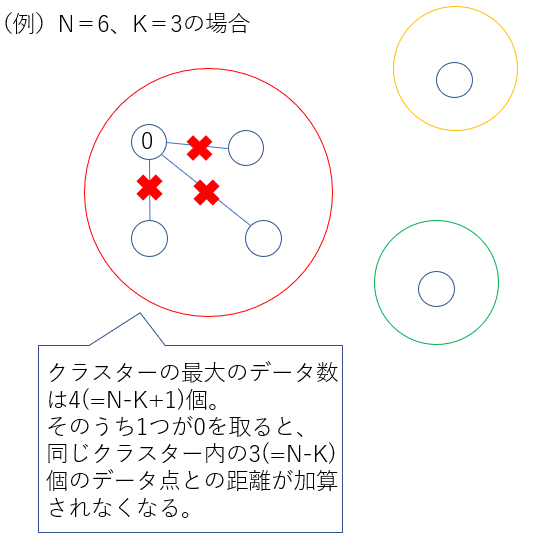
コスト関数$H’$が最も減少するのは、同じクラスター内の$(N-K)$個の点が$x_i$から$d$の最大値だけ離れている場合です。これを数式として表すと以下のようになります。

$$ \sum_{x_j \in C_a}d(x_i,x_j) \leq (N-K) \cdot \max_{x_j \in C_a} d(x_i,x_j) \tag{6}$$

つまり、すべての$i$について以下の不等式を満たすように$\lambda_i = \lambda$と設定すると、ある点をどのクラスターにも割り当てない事によるコスト関数$H’$の減少量が制約違反による$\lambda\Phi_i$の増加量を下回るため、制約違反を防ぐ事ができます。

$$ \lambda \geq (N-K) \cdot \max_{i,j} d(x_i,x_j) \tag{7}$$

実践的には、$d(x_i,x_j)$の値は$ \underset{i,j}{\max} d(x_i,x_j)=1$となるよう正規化されるので、

$$ \lambda = N-K \tag{8}$$

となります。

スピン変数を用いたコスト関数の書き換え

ハードウェア上での数値の精度について考えるために、コスト関数 $H$をスピン変数$s_{i,a}\in\{1,-1 \}$ で書き換えます。$q_{i,a}$ と$s_{i,a}$ は$q_{i,a}=\frac{1}{2}(s_{i,a}+1)$という対応関係にあるため、コスト関数 $H$ は$s_{i,a}$を用いて以下のように書き直されます。

$$
H = \frac{1}{2}\sum^K_{a=1}\sum^N_{i,j=1}d(x_i,x_j)\frac{1}{2}(s_{i,a}+1)\frac{1}{2}(s_{j,a}+1) + \lambda \sum^N_{i=1}\left(\sum^K_{a=1} \left\{\frac{1}{2}(s_{i,a}+1)\right\}-1\right)^2 \tag{9}
$$

コスト関数 $H$を展開して最小化に影響しない定数項を取り除き、全体を4倍すると以下の式が得られます。

$$
\begin{align}
H &= \frac{1}{2}\sum^K_{a=1}\sum_{(i,j)}d(x_i,x_j)s_{i,a}s_{j,a} + \lambda \sum^N_{i=1}\sum_{(a,b)} s_{i,a}s_{i,b} \\ &+ \sum_{(i,j)}d(x_i,x_j)\sum^K_{a=1}s_{i,a} + 2\lambda(K-2)\sum^N_{i=1}\sum^K_{a=1}s_{i,a}
\end{align} \tag{10}
$$

ここで、ハードウェアの制約の下で係数 $\lambda$の最大化を考えます。 $K>2$で、ハードウェアの精度が $n$ ビットである場合、 $\lambda$について以下の等式が成立します。

$$
2 \lambda(K-2) = 2^{n-1}-1 \tag{11}
$$

これと式 $(6)$より、データ間の距離 $d$の大きさについて以下の不等式が成立します。

$$
|d| \leq \frac{2(2^{n-1}-1)}{(N-K)(K-2)} \tag{12}
$$

上記の不等式から、データの個数$N$ が大きくなるほど $d$の最大値が小さくなり、数値の精度が悪化することが分かります。こういった理由から、現代の$6$ビットの量子アニーリングマシンをソルバーに用いる場合には、データの個数$N$ が小さいクラスタリングのみ確実に扱うことができます。

Binary clusteringの定式化

ここでは、 $N$ 個のデータ点を2 個のクラスターに割り当てるという問題を考えます。この場合には、スピン変数を用いてデータ点がクラスター1 に属することを$1$ 、属さない（クラスター2に属する）ことを$-1$ で表現することで、全てのデータ点が必ずいずれか一方のクラスターに割り当てられます。そのためone-hot制約を用いない以下のコスト関数$H$ で定式化されます。

$$
H = \frac{1}{2} \sum^N_{i,j=1}d(x_i,x_j)s_i s_j\tag{13}
$$

$d(x_i,x_j)$の値が大きいほど、$s_i,s_j$は異なる値を取ろうとするため別のクラスターに割り当てられやすくなります。この定式化には制約が存在しないため、数値の精度について心配する必要がありません。さらに、$K=2$の時のOne-hot encodingと比較して使用する量子ビットの数が半分になります。一方で、この定式化は $K=2$の場合にしか対応していません。そのため、より多くのクラスターへの割り当てを扱うには、分割した各クラスターを再度クラスタリングにより分割する階層型クラスタリング等の利用が必要です。

結果

ここまでで提案した定式化によるクラスタリングの性能を、既存手法であるk-meansと比較します。提案手法のソルバーにはハードウェアで実行可能な問題サイズであれば量子アニーリング(QA)マシンを、問題サイズが大きい場合はqbsolvを利用します。qbsolvとは元の大規模な問題を分割し、サイズの小さいそれぞれの問題を個別に解くツールです。本論文では分割後のソルバーにはタブーサーチという局所探索法を用いています。

One-hot encodingの結果

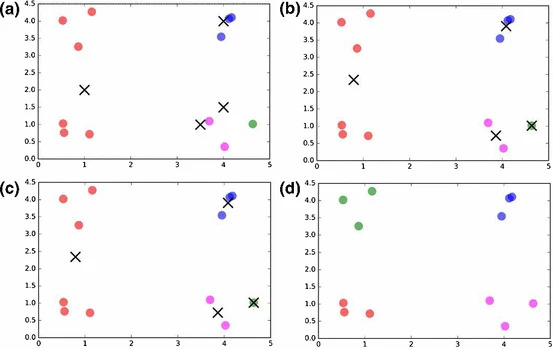
まず、$N=12,K=4$の結果を図 2に示します。(a)~(c)はk-means、(d)はOne-hot encodingにより定式化しQAマシンで解いた結果です。k-meansで解く際、クラスターの中心のうち、一つが二つのクラスターの真ん中に、残りの三つが他の二つのクラスターの近くに初期化されてしまうと最適解を得ることができていません。このような問題はデータ点が$2$次元より大きい空間に属する際により頻繁に起こります。一方、One-hot encodingで定式化しQAマシンで解いた場合には依存する初期値が存在しないため1000サンプル全てで最適解を得ることができました。

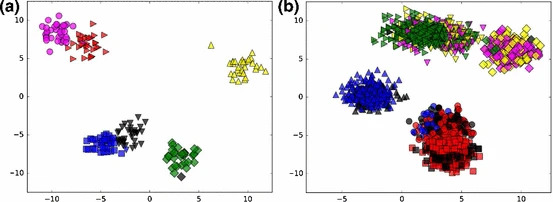
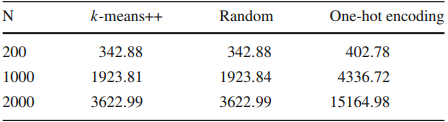
次に、サイズが大きい場合の結果を図3に示します。(a)が $N=200$、(b)が $N=2000$であり、いずれも$K =6$としています。さらに、結果を比較する指標として各手法におけるInertiaを表1にまとめています。Inertiaとは全てのクラスターについて属するデータ点のクラスターの中心からの距離の総和をとったものであり、小さいほどクラスター内のデータ点が近くにまとまっており良い結果となります。なお、k-meansについては、クラスターの中心をランダムに初期化する場合と、中心どうしが離れて配置されるよう初期化をするk-means++を用いた場合の両方で結果を出しています。また、10通りの初期値に対する結果の中でInertiaが最も小さいものを解としています。この場合には、全てのケースでOne-hot encodingはk-meansよりも明らかに劣る結果となりました。この理由について、One-hot encodingは定式化の手法でありクラスタリングの結果は用いたソルバーの性能にも依存する事から、サイズが大きくなったことでqbsolvによる最適化が十分に行えなくなったのだと考えられます。

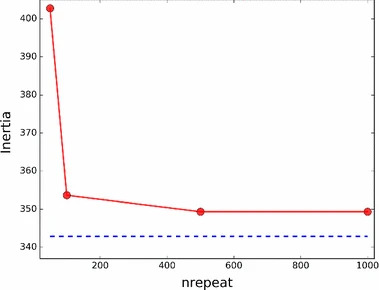
また、上の $N=200$の問題において、qbsolvのパラメーターnum_repeatを変更した際のInertiaの値を図4に示します。num_repeatとはqbsolvによる問題の分割と最適化の試行回数を決めるパラメーターです。num_repeatが大きくなるにつれてInertiaの値が減少し、k-meansの結果に近づいていることがわかります。この結果から、ソルバーを改良するとOne-hot encodingによってより良い解が得られるようになると予想されます。

Binary clustering の結果

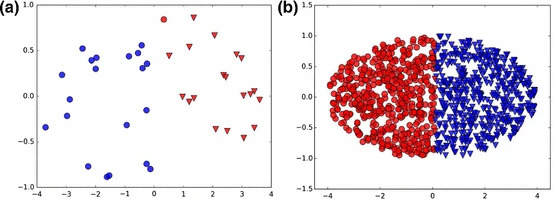
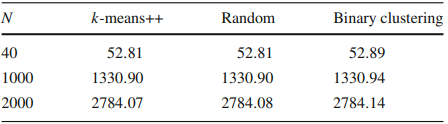
$N＝40$の場合は実際のハードウェアで、 $N=1000,2000$の場合は、qbsolvで問題を解いています。図 5は(a)が $N=40$、(b)が $N＝2000$の問題を解いた結果です。また、各手法のInertiaを表 2にまとめています。Binary clusteringはOne-hot encodingとは異なり、サイズ $N$によらずk-meansの結果と比べわずかな違いしかありませんでした。

結論

本論文では、One-hot encodingとBinary clusteringの2つの手法でクラスタリングを定式化し、量子アニーリングマシンやqbsolvで実行して性能を評価しました。One-hot encodingではデータ点が多い場合にk-meansよりも劣る結果となりました。原因としては、問題を解くために多くの量子ビットが必要であることや、制約の数値精度が十分でないことなどが挙げられます。しかし、ソルバーの質が向上することでよい解が得られると予想されます。対してBinary clusteringではデータのサイズによらずk-meansと比較してもよい結果となりました。制約がなく、使用する量子ビットも少ない事がその理由として考えられます。

あとがき

Binary clusteringではサイズ$N$ が大きくなっても結果が悪化しないが、 $K=2$とかなり使用できる範囲が限られていました。 $K$が3以上でもメモリや数値精度、解の質に問題がないように拡張ができないか興味があります。今回読んだ論文の内容をもとに別な定式化を考えてみたいです。

本記事の担当者

會田裕樹