文献情報

• タイトル : Hybrid Quantum Annealing via Molecular Dynamics
• 著者 : Hirotaka Irie, Haozhao Liang, Takumi Doi, Shinya Gongyo, Tetsuo Hatsuda
• 書誌情報 : https://doi.org/10.1038/s41598-021-87676-z

概要

量子アニーリングは、組合せ最適化問題を近似的に解く量子アルゴリズムです。近年の量子アニーリングマシンの登場により、量子アニーリングの実用的な利用法も広く研究され始めています。

しかし、量子ビット数やノイズ対策にはまだ限界があり、現状の量子アニーリングマシンでは大規模な問題を高精度で解くことができません。そこで、大規模性能を補完する方法の一つとして、量子アニーリングマシンによる小規模な最適化を古典的手法と組み合わせるハイブリッド方式の開発が行われています。

本論文では、古典的手法として分子動力学法を量子アニーリングの前処理に用いる古典・量子ハイブリッド方式を提案します。そして、本手法を用いて最大カット問題とイジングスピングラス問題を解き、得られる解の精度や計算時間を古典的最適化手法 ( タブーサーチやシミュレーテッドアニーリング ) と比較します。

背景

イジングモデルと量子アニーリング

組合せ最適化問題の多くは、$s_i \in \{\pm 1\} $ ( $i=1,\dots,N$ ) をスピン変数、$J_{ij}$ を相互作用、$h_i$ を外磁場とするイジングモデルの基底状態 ( 以下の式 (1) を最小にするようなスピン変数 $s_i$ の組み合わせ ) を探索する問題として表すことができます。

$$
\begin{equation}
\mathcal{H}_{\rm{Ising}}(s)=\frac{1}{2}\sum_{i\ne j}^{N}J_{ij}s_{i}s_{j}+\sum_{i=1}^{N}h_is_i \tag{1}
\end{equation}
$$

そして、量子アニーリング ( QA : Quantum Annealing ) は、以下の量子ハミルトニアン $\mathcal{H}_{\rm{QA}}$ を時間発展させ、式 (1) の基底状態を求める手法です。

$$
\begin{equation}
\mathcal{H}_{\rm{QA}}(\sigma ; \tau)=A(\tau)\left[ -\sum_{i=1}^{N}\sigma_i^{x} \right] +B(\tau)\left[ \frac{1}{2}\sum_{i\ne j}^{N}J_{ij}\sigma_{i}^{z}\sigma_{j}^{z}+\sum_{i=1}^{N}h_i \sigma_i^{z} \right] \tag{2}
\end{equation}
$$

ここで $\sigma_i^x$ と $\sigma_i^z$ は、それぞれ各 $i$ ( $=1,2,\cdots,N$ ) における $2\times2$ のパウリ行列の $x$ 成分と $z$ 成分を表します。また、$\tau$ は時間 $t$ に依存する関数であり、その値域は $[0,1]$ です。そして、スケジューリング関数 $A(\tau)$ および $B(\tau)$ は、初期 ( $\tau=0$ ) に $A(0)\gg B(0)$、終期 ( $\tau=1$ ) に $A(1)\ll B(1)$ となるように選びます。

量子アニーリングを実行するマシンのことを量子アニーリングマシンと言います。量子アニーリングマシンとしては D-Wave Systems が開発した D-Wave マシンがあり、本論文でも使用されています。しかし、現状の D-Wave マシンは、ノイズ対策や量子ビット数に限界があるため、変数の数が多い ( = 規模の大きい ) 最適化問題の解を正確に求めるのは難しいのが現状です。そこで、本論文では、量子アニーリングの前処理として分子動力学法を用いることにより、量子アニーリングで探索する解の領域を削減する工夫を行っています。

分子動力学法

分子動力学法 ( MD : Molecular Dynamics ) とは、分子や原子といった粒子の運動方程式を数値的に解くことにより、多数の粒子の運動を追跡する手法です。生体分子を構成する原子の解析や、液体中の衝撃波に関する実験など、計算機シミュレーションの方法として様々な分野で利用されています。

上述の通り、MD では粒子それぞれの運動方程式を繰り返し解きますが、それは以下に示す古典ハミルトニアン $\mathcal{H}(\{q_i\},\{p_i\})$ の正準方程式を解くことと等価であることが知られています ( 添字 $i$ は粒子一つひとつの番号です )。[1]

$$
\begin{equation}
\frac{d q_i}{d t}=\frac{\partial \mathcal{H}}{\partial p_i}\ ,\ \frac{d p_i}{d t}=-\frac{\partial \mathcal{H}}{\partial q_i} \tag{3}
\end{equation}
$$

ここで、$q_i$ は一般座標、$p_i$ は一般運動量です。古典ハミルトニアン $\mathcal{H}$ は、$q_i$ と $p_i$ を変数とし、系全体のエネルギーを表現する関数です。したがって、系に存在する粒子同士の相互作用などの情報を全て含んでいます。

式 (3) の正準方程式を繰り返し解いて粒子の時間発展を計算していくメリットは、古典ハミルトニアンを適切に設計することにより、エネルギー最小化を行うことができる点です。したがって、イジングモデルの基底状態を探索するような古典ハミルトニアン $\mathcal{H}$ を設計すれば、MD によって組合せ最適化問題の解を求めることができます。よって、そのような古典ハミルトニアンを設計することが目標となります。

手法

手法の概要

本論文では、MD と QA を組み合わせた新しい量子最適化システム HQA ( Hybrid Quantum Annealing ) を提案しています。以下の図 1 に、HQA の概念図を示します。

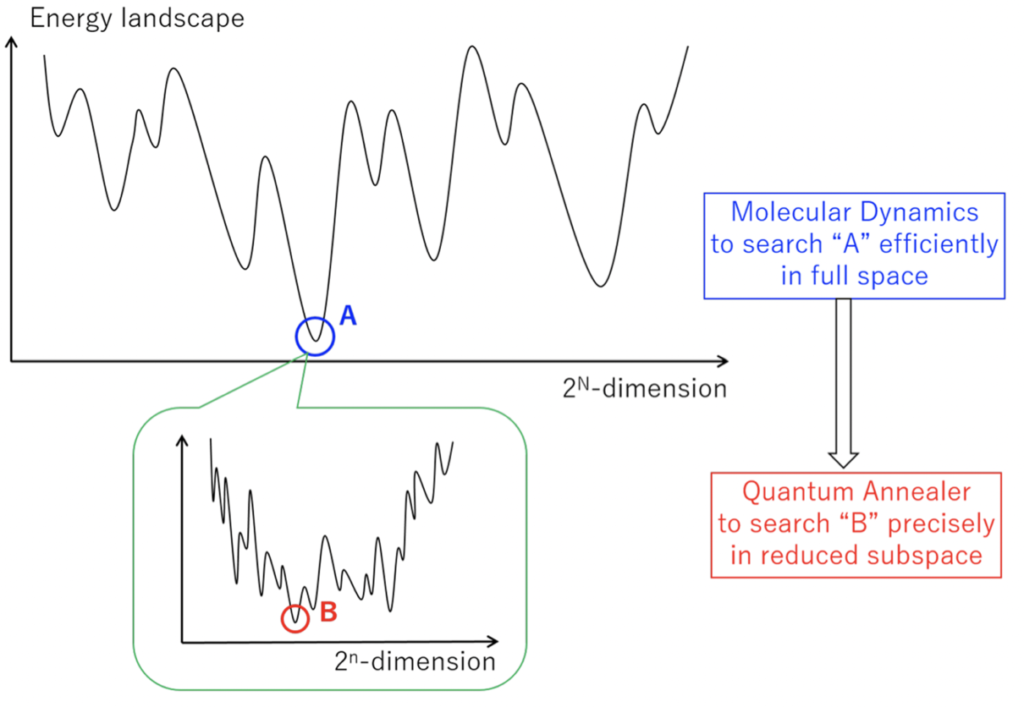
図 1 が示すように、HQA では、はじめに変数 $N$ 個の最適化問題に MD を適用します。これにより、問題サイズを $n$ 個にまで絞り込みます。そして、残る変数 $n$ 個の部分問題に QA を適用し、$N$ 変数全ての最終的な解を得ます。

古典ハミルトニアンの設計

ここでは、MD を用いてイジングモデルの基底状態を求めるための古典ハミルトニアン $\mathcal{H}_{\rm{MD}}$ を設計します。そのような $\mathcal{H}_{\rm{MD}}$ は、以下の式 (4) のように記述することができます。

$$
\begin{equation}
\mathcal{H}_{\rm{MD}}(\varphi,p ; \tau)=\alpha(\tau)\sum_{i=1}^{N}\left( \frac{p_i^{2}}{2}+V(\varphi_i) \right) + \beta(\tau)\left[ \frac{1}{2}\sum_{i \ne j}^{N}J_{ij}\varphi_i \varphi_j + \sum_{i=1}^{N}h_i|\varphi_i|\varphi_i \right] \tag{4}
\end{equation}
$$

ここで、$\varphi_i$ ( $i=1,\cdots,N$ ) は連続 flux 変数、$p_i$ ( $i=1,\cdots,N$ ) は連続共役運動量です。flux 変数 $\varphi_i$ は、イジングモデルのスピン変数に対応します。ただし、向き $\{+1,-1\}$ だけでなく、大きさ $|\varphi_i|$ を持ちます。MD の時間発展は $\tau=t\ / \ t_{f}\in[0,1]$ とします。したがって、$t\in [0,t_{f}]$ が実際の発展時間に対応します。また、スケジューリング関数 $\alpha(\tau)$、$\beta(\tau)$ は QA と同様、初期 ( $\tau=0$ ) は $\alpha(0)\gg \beta(0)$、終期 ( $\tau=1$ ) は $\alpha(1)\ll \beta(1)$ となるように選びます。

そして、ポテンシャル項 $V(\varphi)$ は $V(\varphi)=\varphi^{M} \ (M=4,6,8,\cdots)$ という下に凸の関数です。この項には、flux 変数 $\varphi_i$ の絶対値 $|\varphi_i|$ を時間発展に伴って大きくする効果があります。

式 (4) を、式 (2) の QA のハミルトニアンと比較してみます。式 (4) の第一項は、各 flux 変数が初期に $\varphi_i=0$ の周りで振動することを保証します。これは、式 (2) の第一項が、初期に各スピンを重ね合わせ状態にするのと似た役割になっています。式 (4) の第二項は、式 (2) の第二項と同様、イジングモデル ( 式 (1) ) を表す項です。式 (2) と式 (4) は、いずれも終期 ( $\tau=1$ ) で第二項のイジングモデルの基底状態を得ることを目的として設計されています。

この $\mathcal{H}_{\rm{MD}}$ に関して、以下の正準方程式を解くことによって flux 変数の時間発展を計算します。

$$
\begin{equation}
g \frac{d\varphi_i}{d\tau}=\frac{\partial \mathcal{H}_{\rm{MD}}(\varphi,p ; \tau)}{\partial p_i},\qquad g \frac{d p_i}{d\tau}=-\frac{\partial \mathcal{H}_{\rm{MD}}(\varphi,p ; \tau)}{\partial \varphi_i} \tag{5}
\end{equation}
$$

ここで、$\tau=(\ t\ /\ {t_{f}})\equiv g t$ です。 $g \to 0$ のとき、flux 変数の運動は断熱的になります。本論文では、式 (5) を GPGPU マシン上で leapfrog algorithm を用いて解いています。leapfrog algorithm とは、微分方程式の数値計算法の一つで、古典力学系の計算でよく用いられる手法です。[1]

初期条件については、$\varphi_i(\tau=0)=0$ とし、$p_i(\tau=0)$ は $+1$ または $-1$ にランダムに選択します。また、凸ポテンシャル $V(\varphi)$ については、$M = 4, 6, 8$ をテストし、$M = 6$ が発展時間と精度の点で最も良い性能を示したため、この論文ではこの値を使用しています。

用語の導入 – frozen 変数と ambivalent 変数 –

上で設計した古典ハミルトニアン $\mathcal{H}_{\rm{MD}}$ について、試験的に MD 発展を行います。イジングモデルのパラメータ $J_{ij}$ および $h_i$ は、$-1\le J_{ij} \le+1$、$-2\le h_i \le +2$ の区間からランダムな値を 1 ペア選びます。図 2 は、そのときの flux 変数の全軌道 $\{\varphi_i\}\ (i=1,\cdots,10,000)$ です。ここで、MD 時間ステップ $\delta \tau$ は $\delta \tau=1\ / \ 50,000$ とします。

また、QA のような断熱的時間発展を模倣したシミュレーションをするには、式 (5) で $g\to 0$ とする必要がありました。したがって、$g$ には小さな値を選ばなくてはなりません。そこで、ここでは $g=\delta \tau\ (=1 \ / \ 50,000)$ としています。

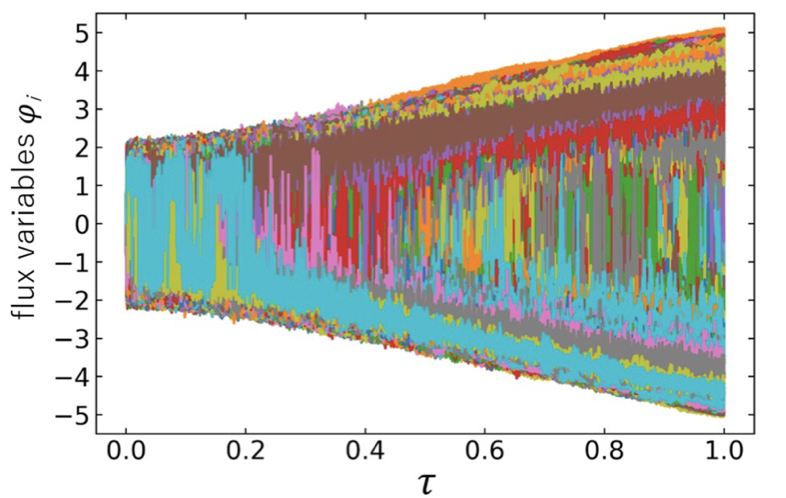
図 2 には全ての flux 変数の軌道が色分けされて示されています。一番手前に見える水色の軌道を見ると、初期は $\varphi_i=0$ の周りで振動していますが、終期は振動が小さくなり、負の方向に落ち着いていることが分かります。また、茶色の軌道を見ると、初期の軌道は隠れていますが、徐々に正の方向に落ち着いています。一方で、終期になっても $\varphi_i=0$ の周りで振動し続けている軌道も見られます。このように、各 flux 変数の軌道は ｢ 正に落ち着く ｣、｢ 負に落ち着く ｣、｢ $\varphi_i=0$ の周りで振動し続ける ｣ という 3 つの傾向に分けられることが分かりました。

次に、これらの傾向を定量的に分ける基準として、以下の式 (6) で表される flux 変数の時間平均を考えます。

$$
\begin{equation}
\overline{\varphi}_{i}(\tau)\equiv \frac{1}{\delta}\int_{\tau-\delta}^{\tau}d \tau’ \varphi_i(\tau’) \tag{6}
\end{equation}
$$

ここで、区間 $\delta$ は MD ステップ $\delta \tau$ より十分大きく、かつ $1$ より十分小さいものとします。以下の図 3 に式 (6) の概念図を示します。

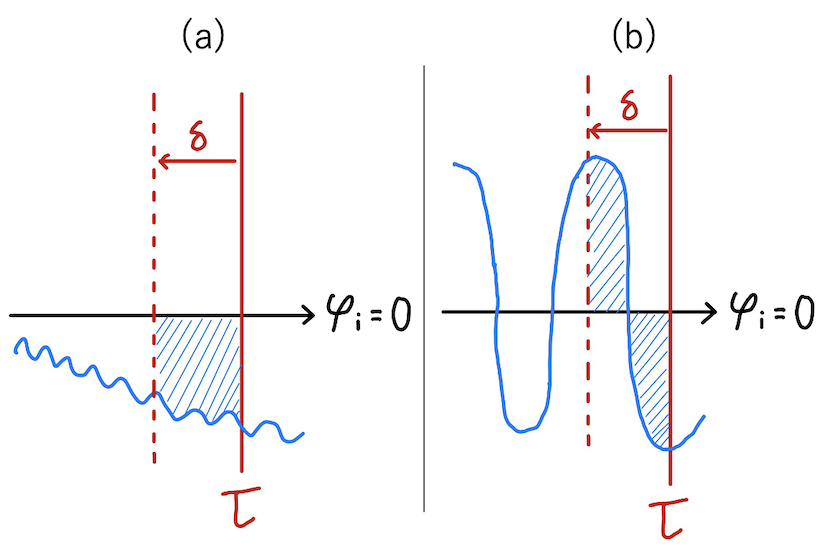
図 3(a) では、flux 変数の軌道が負に落ち着く場合の積分値 $\overline{\varphi}_{i}(\tau)$ を青の斜線で示しています。また、図 3(b) では、軌道が $\varphi_i=0$ の周りで振動し続ける場合の $\overline{\varphi}_{i}(\tau)$ を青の斜線で示しています。図 3(b) の場合は、$\overline{\varphi}_{i}(\tau)$ に正の領域と負の領域があるため、その絶対値 $| \overline{\varphi}_{i}(\tau) |$ は図 3(a) に比べて小さくなります。したがって、$\varphi_i=0$ の周りで振動し続ける場合の $| \overline{\varphi}_{i}(\tau) |$ の値は、軌道が正 ･ 負に落ち着く場合より小さくなることが分かります。

よって、終期 $\tau=1$ での $|\overline{\varphi}_{i}(\tau)|$ の値 ( $|\overline{\varphi}_{i}(\tau=1)|$ ) で並べ替えることにより、$|\overline{\varphi}_{i}(\tau=1)|$ が小さい方を ｢ $\varphi_i=0$ の周りで振動し続ける変数 ｣、$|\overline{\varphi}_{i}(\tau=1)|$ が大きい方を ｢ 正・負に落ち着く変数 ｣ という様に分けることができます。本論文では、前者を ambivalent 変数と呼び、後者を frozen 変数と呼んでいます。具体的には、ambivalent 変数と frozen 変数は以下の図 4 のように定義されます。

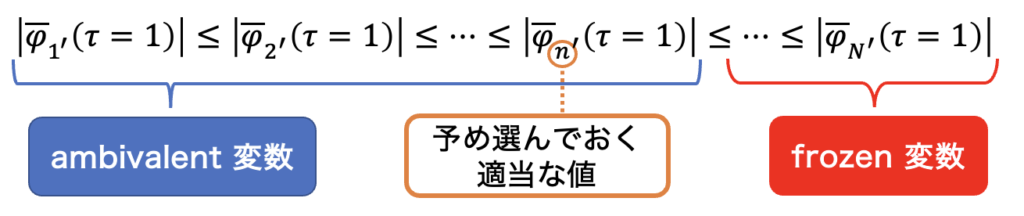
図 4 において、$i’$ はソート後のインデックスです。したがって、$\{\varphi_{i’}\} \ (i’=1,\cdots,n)$ が ambivalent 変数で、$\{\varphi_{i’}\} \ (i’=n+1,\cdots,N)$ が frozen 変数です。ambivalent と frozen を分ける整数 $n\ (<N)$ については、予め適当な値を選んでおきます。

ハイブリッド量子アニーリング

MD とソートの組み合わせにより、flux 変数を frozen 変数と ambivalent 変数に分けることができました。frozen 変数は、値の正 ･ 負が定まっているため、解きたい最適化問題に対する解が確定している変数とみなすことができます。それは、スピン変数の取り得る値は $-1$ か $+1$ であるため、$s_{k’}=\rm{sgn}({\varphi}_{k’}(\tau=1))$ として符号を取り出せば良いからです。ここで、${\rm sgn}(x)$ は $x>0$ のときに $+1$、$x<0$ のときに $-1$ を返す符号関数です。これにより、frozen 変数に関してはスピンの向き $\{+1,-1\}$ を固定することができます。

一方の ambivalent 変数は、解きたい問題に対する解がまだ確定していない変数です。本論文では、この ambivalent 変数に対して QA ( もしくは他のイジングソルバ ) を使用します。具体的には、ambivalent スピン $\{s_i\}\ (i’=1,\cdots,n)$ について以下のイジングモデルを定義し、その基底状態を QA ( もしくは他のイジングソルバ ) によって求めます。

$$
\begin{equation}
\mathcal{H’}_{\rm{Ising}}(s)=\frac{1}{2}\sum_{i’\ne j’}^{n}J_{i’j’}^{\rm{eff}}s_{i’}s_{j’}+\sum_{i’=1}^{n}h_{i’}^{\rm{eff}}s_{i’}\equiv \mathcal{H}_{\rm{Ising}}(s|s_{k’=n+1,\dots,N} : \rm{frozen})-(\rm{const.}) \tag{7}
\end{equation}
$$

ここで、$J_{i’j’}^{\rm{eff}}$ と $h_{i’}^{\rm{eff}}$ は frozen スピン $\{s_i\}\ (i’=n+1,\cdots,N)$ の値を代入することによって以下のように求められます。

$$
\begin{equation}
J_{i’j’}^{\rm{eff}}=J_{i’j’}, \quad h_{i’}^{\rm{eff}}=h_{i’}+\sum_{k’=n+1}^{N}J_{i’k’}s_{k’},\quad(i’,j’=1,2,\dots,n) \tag{8}
\end{equation}
$$

以下の図 5 は、$N$ 変数の最適化問題を解く HQA の全体像を示すフローチャートです。

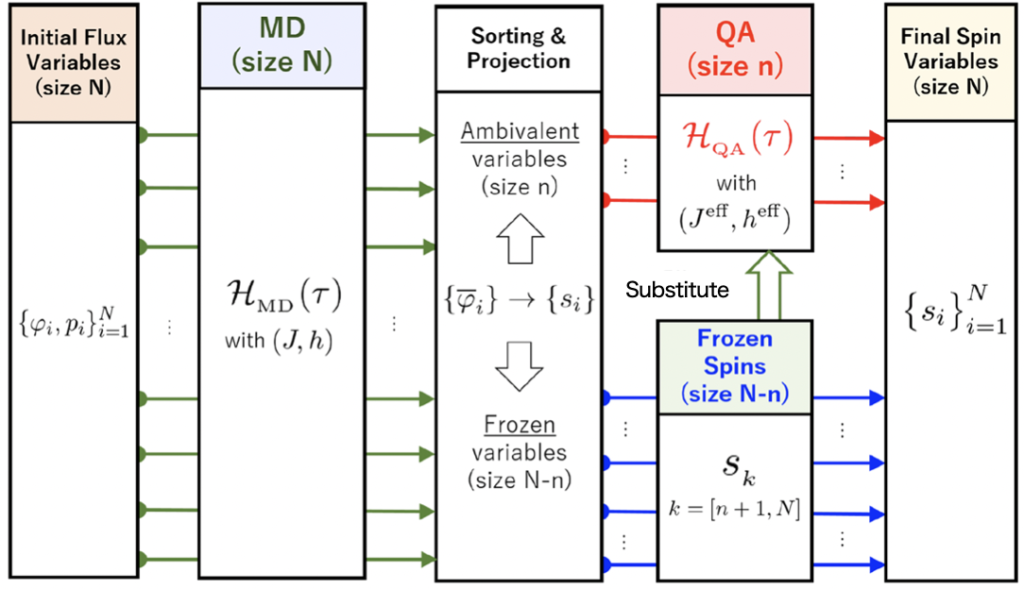
図 5 に示すように、HQA では、はじめに $N$ 変数の最適化問題に MD を適用し、$\overline{\varphi}_i$ の値でソートすることによって $N-n$ 個の frozen 変数と $n$ 個の ambivalent 変数に分けます。そして、frozen 変数は符号を取り出して最終的なスピンの値として固定し、ambivalent 変数は QA ( もしくは他のイジングソルバ ) によってスピンの値を求めます ( ただし、このとき最小化するイジングモデルには、既に確定している frozen スピンの値を代入します )。これにより、最終的な $N$ 個のスピンの値を得ることができます。

結果

実験 1 : 最大カット問題

実験 1 の設定

ここでは、最大カット問題を用いて HQA の解の精度を検証します ( 最大カット問題の定義や例については用語集：最大カット問題にて説明しています[2] )。本実験で用いる最大カット問題は、$K_{2000}$ と呼ばれる 2000 ノードの完全グラフ上の問題です。完全グラフとは、全ての頂点同士が点で結ばれているグラフのことを言います。$K_{2000}$ では、$J_{ij}=\pm 1$ をランダムに選びます。このランダムな問題を 100 個生成し、それぞれについて求めた最大カットの平均値を算出することにより、各ソルバの典型的な性能を評価します。

この実験では、以下の 5 つのケースで解の精度を比較します。

1. MD のみ ( 前処理だけ ) : MD と略記
2. MD と QA ( D-Wave_2000Q_5 ) によるHQA ( $n=48$ ) : HQA(DW48) と略記
3. MD と古典タブーサーチ ( QBSolv ) による HQA ( $n=1000$ ) : HQA(TS1000) と略記
4. シミュレーテッドアニーリング ( dwave.neal ) : SA と略記
5. タブーサーチ ( QBSolv ) : TS と略記

SA と TS は、HQA や MD との比較のために用いる古典的な最適化手法です。SA は、焼きなまし法とも呼ばれ、物質を過熱した後に温度を徐々に下げることでエネルギーを最小化する物理的プロセスに由来します。温度を一段回下げる過程をスイープと呼びますが、その回数を本実験では $N_{\rm{sw}} =1000$ とします。SA 全体で、逆温度 $\beta$ はスイープごとに $\beta_{\rm{I}}=0.01$ から $\beta_{\rm{F}}=1.0$ まで増加させます ( 逆温度は温度 $T$ の逆数 ( $\beta = 1\ / \ T$ )なので、スイープごとに温度を下げていくことに対応します )。TS は、探索済みの領域をタブーリストに入れることにより再度探索することを避けながら、現時点での解の近傍を局所探索していくアルゴリズムです。

実験 1 の結果

以下の図 6 に、各ソルバによって得られた最大カットを示します。横軸は MD ステップ $(\delta \tau)^{-1}$ で、縦軸は最大カットです。したがって、縦軸の値が大きいほど解の精度は良いと言えます。各線に付いている薄色の帯は $\pm 1 \sigma$ の信頼区間を表しています ( $\sigma$ は標準偏差 )。また、$C^{\ast}$ は、統計力学的な解析によって求めた $K_{2000}$ のおおよその理論値です。

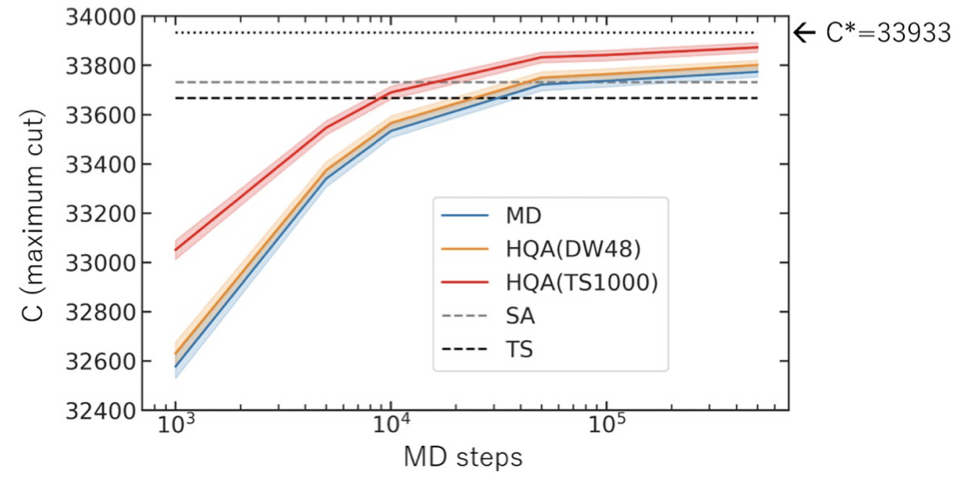
図 6 から、MD ステップ数を増やすほど、MD および HQA の精度は向上していることが分かります。また、MD 単独では $500,000$ 回の MD ステップで $C^{\ast}$ から $0.4\%$ の誤差まで到達しています。ここでの誤差とは、該当する最大カット $C$ に対して、${100\times(C^{\ast}-C)}/{C^{\ast}}\ (\%)$ で求められる割合です。すなわち、この値が小さいほど精度が高いと言えます。

$500,000$ 回の MD ステップと同等の計算時間で得られた SA の精度は誤差 $0.6\%$、TS の精度は誤差 $0.8\%$ であるため、MD 単独で他の古典ソルバよりも高い精度が出ていることが確認できます。さらに、( 500,000 MD ステップ ) + ( QA or TS ) のハイブリッド方式 HQA について、HQA(DW48) は誤差 $0.3\%$、HQA(TS1000) は誤差 $0.2\%$ の精度まで向上しています。MD を用いたソルバの精度を比較すると、いずれの MD ステップにおいても MD $<$ HQA(DW48) $<$ HQA(TS1000) となっており、HQA(TS1000) が最も高精度になっています。

実験 2 : イジングスピングラス問題

実験 2 の設定

ここでは、イジングスピングラス問題を用いて HQA の解の精度を検証します。この問題では、イジングモデルのパラメータである $J_{ij}$ と $h_i$ を、それぞれ区間 $-1\le J_{ij}\le +1$ と $-2\le h_i \le +2$ からランダムに選びます。このランダムな問題を 100 個生成して、それぞれについて求めた最小エネルギーの平均値 $E\equiv \left\langle \mathcal{H}_{\rm{Ising}}^{(\rm{min})(s)} \right\rangle$ を算出することにより、各ソルバの典型的な性能を評価します ( エネルギーは式 (1) の $\mathcal{H}_{\rm{Ising}}$ の値です )。

この実験では、以下の 6 つのケースで解の精度を比較します。

1. MD のみ ( 前処理だけ ) : MD と略記
2. MD と QA ( D-Wave_2000Q_5 ) による HQA ( $n=48$ ) : HQA(DW48) と略記
3. MD と古典タブーサーチ ( QBSolv ) によるHQA ( $n$ が小さい場合 ) : HQA(TS( $n$ の値 )) と略記
4. MD と古典タブーサーチ ( QBSolv )による HQA ( $n$ が大きい場合 ) : HQA(TS( $n$ の値 )) と略記
5. シミュレーテッドアニーリング ( dwave.neal ) : SA と略記
6. タブーサーチ ( QBSolv ) : TS と略記

SA のスイープ回数は実験 1 と同様、$N_{\rm{sw}} =1000$ とし、逆温度 $\beta$ はスイープごとに $\beta_{\rm{I}}=0.01$ から $\beta_{\rm{F}}=1.0 $ まで増加させます。

また、本実験では、問題サイズ $N$ を $N = 1000,\ 2000,\ 10000$ と変化させ、問題サイズに対する各ソルバの依存性を評価します。さらに、HQA(TS) については、整数 $n$ の値を変化させ、$n$ の大きさによる精度の違いも確認します。具体的には、$N=1,000$ のときに $n=500$ と $n=800$、$N=2,000$ のときに $n=500$ と $n=1,000$ 、$N=10,000$ のときに $n=1,000$ と $n=4,000$ を比較します。

実験 2 の結果

以下の図 7 に、各ソルバによって得られた最小エネルギーを示します。横軸は MD ステップ $(\delta \tau)^{-1}$ で、縦軸はエネルギーの値です。したがって、縦軸の値が小さいほど解の精度は良いと言えます。

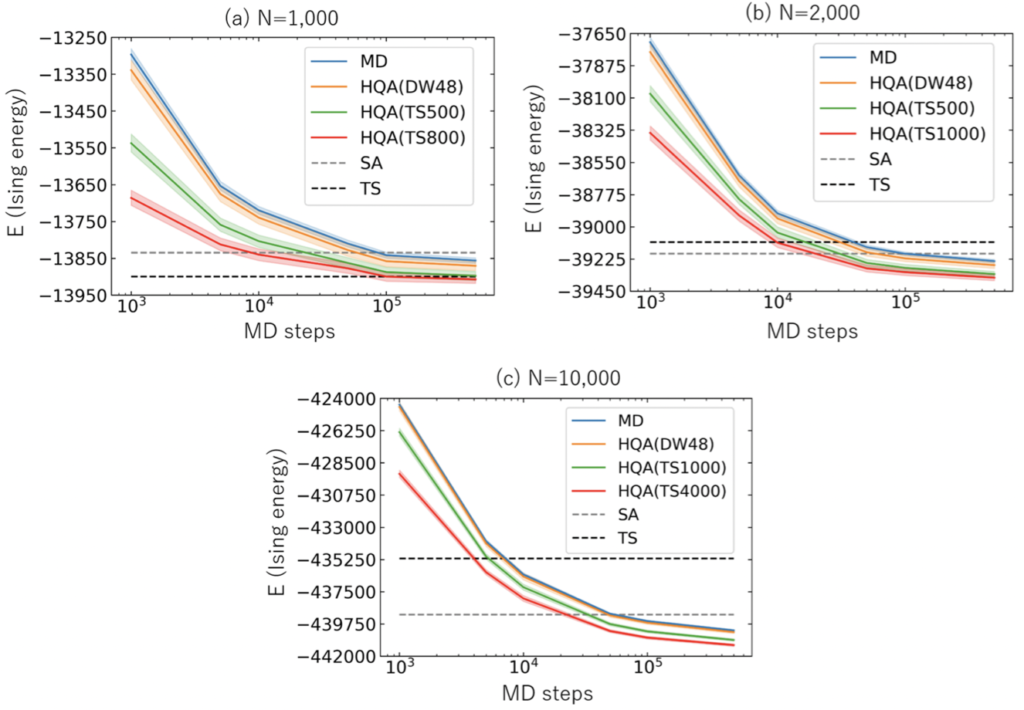
図 7 から、いずれの問題サイズにおいても、MD ステップ数を増やすほど、MD を用いたソルバの精度は向上していることが分かります。また、これらの精度は、いずれの MD ステップにおいても MD $<$ HQA(DW) $<$ HQA(TS( $n$ が小さい場合 )) $<$ HQA( TS( $n$ が大きい場合 )) となっており、HQA(TS( $n$ が大きい場合 )) が最も高精度になっています。HQA(DW) よりも HQA(TS) が高精度なのは実験 1 と同様の結果ですが、$n$ が大きくなると、HQA(TS) の精度はさらに向上しています。すなわち、ambivalent とみなして TS で解く変数を増やした方が良い精度が出ていることになります。

$500,000$ 回の MD ステップと同等の計算時間で得られた SA や TS の精度と比較すると、$N=1,000$ では、MD を用いたソルバはおおよそ SA 以上、TS 以下の精度となっています。そして、$N=2,000$ になると、MD を用いたソルバは全て SA と TS の精度を超えており、さらに$N=10,000$ では、SA と TS の精度を大きく凌駕しています。

したがって、MD を用いたソルバは、問題サイズが大きくなるにつれて、SA や TS と比較したときに精度が向上することが確認できました。

結論

本論文では、分子動力学法を量子アニーリングの前処理に利用する古典 ･ 量子ハイブリッド方式 HQA を開発しました。

本手法で最大カット問題 $K_{2000}$ を解いた結果、HQA(TS1000) が同等の計算時間の SA や TS に比べて最も良い精度となりました。また、イジングスピングラス問題を解いた結果、問題サイズ $N$ が $2,000$ や $10,000$ になると、MD を用いたソルバは SA や TS を超える精度となり、HQA(TS ( $n$ が大きい場合 )) が最も良い精度となりました。

以上の結果から、HQA によって、問題サイズが数千変数を超える大規模な組合せ最適化問題を高精度で解けることが分かりました。したがって、本手法によって QA の大規模性能を補完することができたと言えます。

あと書き

分子動力学法という古典力学に基づく計算機シミュレーション法を連続最適化の手法として用いることにより、組合わせ最適化問題を解くことができる点が面白いと感じました。

また、量子アニーリングの前処理として使用する連続最適化手法を分子動力学法以外のものに変えた時に、得られる解の精度や計算時間にはどのような違いが現れてくるかに興味を持ちました。

さらに、本論文では ambivalent 変数と frozen 変数を適当な整数 $n$ で分けていましたが、量子アニーリングで解く必要のある ambivalent 変数をさらに削減するための工夫を検討したいと感じました。それに関連して、ambivalent 変数の中でも殆ど符号が固定されている ( frozen な ) 変数を活かしたリバースアニーリング [3] の適用も効果的なのではないかと考えました。

参考文献

1. 神山新一 ･ 佐藤明 : 分子シミュレーション講座 分子動力学シミュレーション (新装版) , 朝倉書店 (2020)．
2. T-Wave 用語集 最大カット問題 : https://qard.is.tohoku.ac.jp/T-Wave/?p=3866
3. T-Wave 用語集 リバースアニーリング : https://qard.is.tohoku.ac.jp/T-Wave/?p=2306

本記事の担当者

高林泰成 ( メンタリング : 羽場廉一郎 )