文献情報
- タイトル: The simplest model of jamming
- 著者: Silvio Franz and Giorgio Parisi
- 書誌情報: https://iopscience.iop.org/article/10.1088/1751-8113/49/14/145001
概要
統計力学と組合せ最適化の関連は長らく指摘されています.特に,充足可能性問題 (SAT) やグラフ彩色問題などの,離散変数の 制約充足問題 (Constraint Satisfaction Problem, 以下 CSP) に対しては,統計物理学の観点からの研究が進んでいます.例えば,[1] では,ランダムな SAT インスタンスの性質をスピングラス理論の手法を用いて解析し,制約の個数と変数の個数の比を変えると相転移が起こることを示しました.また,スピングラス理論の手法を転用して,SATインスタンスを解く効率的なアルゴリズムを提案しました.
一方で,連続変数 CSP に対する統計力学的な研究はあまりなされていません.本論文では,ガラスのモデルとして統計物理学で研究されている「球のパッキング」問題が,連続変数 CSP として捉えられることに着目します.球のパッキングは「ジャミング転移」と呼ばれる相転移現象を示すことが知られています.本論文では,連続変数 CSP の単純な例であるパーセプトロンの挙動を統計力学の手法を用いて解析し,球のパッキングと同様のジャミング転移が起こることを示します.
本研究の結果より,多くの連続変数 CSP がジャミングという共通の性質を持つことが予想されます.また,球のパッキングよりも扱いやすい問題であるパーセプトロンがジャミング現象を示すことが明らかとなったことから,パーセプトロンをより詳細に調べることで,ジャミングに対する理解が深まることが期待されます.
背景
しばらく,背景となる統計物理学の知識の簡単な説明をしたのちに,それらをまとめて本研究の貢献について述べます.
相転移と臨界現象
相転移とは,物理系の物理量が急激に変化する現象です.例えば,水の融解 (固体から液体への変化) と蒸発 (液体から気体への変化) は,水の温度を上げていくにつれ,それぞれ $0$ ℃と $100$ ℃を境に水の密度が急激に変化する相転移の例です.他にも,鉄がある温度で強磁性 (磁石にくっつく状態) から常磁性 (磁石にくっつかない状態) へ変化する現象も相転移です.
臨界現象とは,物理系の相転移点での振る舞いです.転移点付近で,物理量はしばしばべき乗則に従います.例えば,鉄の強磁性から常磁性への転移では,温度 $T$ においての磁化 $m(T)$ は臨界温度を $T_c$ として
$$
m(T) \propto (T_c-T)^\beta \
\beta \approx 0.325
$$
のように振る舞うことが知られています.このべき乗則の指数 $\beta$ は臨界指数と呼ばれ,臨界現象を特徴づける値として興味の対象となっています.
先程の臨界指数 $\beta \approx 0.325$ は,鉄の強磁性・常磁性の転移に特有の値ではなく,実は強い普遍性を持っています.他の多くの物質の強磁性・常磁性転移でも同じ臨界指数を示すばかりか,一見全く異なる現象でも同じ臨界指数を持つと考えられているものがあります.例えば,水の液体から気体への転移において密度は不連続に変化しますが,その変化量を $\Delta \rho(T)$ とすると,
$$
\Delta \rho(T) \propto (T_c-T)^\beta \
\beta \approx 0.325
$$
という,強磁性・常磁性転移と同じ臨界指数を持つ臨界現象を示すことが確認されています.同じ臨界指数を持つ系は同じ普遍性クラスに属すると言われ,系の詳細によらない普遍的な性質を反映していると考えられています.さまざまな相転移現象を普遍性クラスへ分類することは,統計物理学の大きな目標の一つとなっています.
スピングラス理論
Ising 模型は,$N$ 個のスピン $s_i$ ($s_i$ は $\pm 1$ の2値を取る変数) からなる系であり,ハミルトニアンは次式で定義されます.
$$
E({s_i}) = \sum_{i,j} J_{i,j} s_i s_j
$$
$J_{i,j}$ は結合定数と呼ばれ,スピン $s_i$ と $s_j$ の間の相互作用を表します.$J_{i,j}<0$ のときは $s_i,s_j$ が同じ向きを向くのが,$J_{i,j}>0$ のときは $s_i,s_j$ が異なる向きを向くのがそれぞれエネルギーが小さくなり,安定になります.
特に, $J_{i,j}$ を負の定数とした最も基本的な模型は,磁石や鉄などの強磁性体のモデルとして用いられます.このモデルでは,各スピンの向きが揃うのが安定な状態であり,これは磁石の性質を捉えています.
スピングラス模型は,結合定数 $J_{i,j}$ が結合によってランダムな値を取るモデルです.このモデルでは,どのようにスピンの値を決めても, $J_{i,j}s_is_j>0$ となる不安定な結合が生じます.この不安定さはフラストレーションと呼ばれ,これによりスピングラス模型は複雑な挙動を示します.スピングラス模型のエネルギーは,下図に示すように多数の極小値を取ります.それぞれの谷は「状態 (state)」と呼ばれ,これらは非常に大きなエネルギーの壁で遮られています.
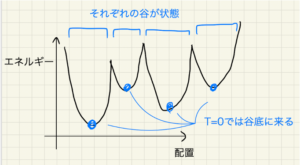
図1: 状態の模式図
スピングラス模型を分析する手法は統計物理学において大きく発展しています.次節で紹介するレプリカ法が代表的な手法です.
レプリカ法
本節では,レプリカ法の計算の詳細には触れず,手法のイメージを定性的に説明します.また,スピングラス理論で重要な概念である「レプリカ対称性」について説明します.
前節で説明したように,スピングラス模型のエネルギー地形は多くの状態に分かれます.系は,いずれかの状態をランダムに取ることになります.そこで,各状態にある系の振る舞いの平均値を取れば,ランダムな系の平均的な振る舞いがわかります.
そこで,解析したい系の同一のコピー (レプリカ) をたくさん作ったとしましょう.これらのレプリカは,それぞれがいずれかの状態をランダムに取ります.系の多数のレプリカを一つの大きな系と見て,その振る舞いを調べれば,元の系の平均的な振る舞いがわかるでしょう.これが,レプリカ法のアイデアです.
もし,状態が一つしかない,つまりエネルギー地形に谷が一つしかない場合,すべてのレプリカは同じ状態に入ります.このとき,どのレプリカも互いに区別できず,レプリカの入れ替えについて対称となります.これを「レプリカ対称性」 (Replica Symmetry, RS) と呼びます.
状態が多数ある場合は,それぞれのレプリカが異なる状態に入り,レプリカの入れ替えについての対称性が破れます.これを「レプリカ対称性の破れ」 (Replica Symmetry Breaking, RSB) と呼びます.
離散変数 CSP の相転移
相転移を起こす系は物理系に限りません.CSP (制約充足問題) も相転移を起こすことが知られています.
CSP とは,いくつかの制約を満たす変数の値の割り当てが存在するかどうか判定する問題です.例えば,K-SAT は,与えられた論理式を満たすような,真偽変数への値の割り当てが存在するか判定する CSP です.他には,グラフ彩色は,与えられたグラフに対して,同じ色が隣り合わないように各頂点に色を割り当てる CSP です.また,これらの例はどれも変数の値が離散的な値を取るため,離散変数 CSP になります.
離散変数 CSP はしばしば相転移を起こすことが知られています.変数の数を $N$, 制約の数を $M$ とし,比 $\alpha = M/N$ を変えると, $\alpha$ が小さいときは制約が少なく,制約の充足が容易であるのに対し, $\alpha$ が大きいときは制約が多く,すべての制約を充足することが難しくなります. $\alpha$ を固定して $N\to \infty$ の極限を考えると, $\alpha$ が小さい領域ではほとんどのインスタンスが充足可能であり, $\alpha$ が大きい領域ではほとんどのインスタンスが充足不可能となります.さらに,充足可能性の変化は急激に起こります. つまり,ある臨界値 $\alpha_c$ が存在して, $\alpha < \alpha_c$ では充足可能, $\alpha > \alpha_c$ では充足不可能となります.このように,充足可能性が急激に切り替わる相転移を SAT-UNSAT 転移と呼びます.
離散変数 CSP は Ising 模型などの離散的な変数を持つ統計力学模型に置き換えて解析することができます.例えば, [1] では K-SAT を Ising 模型に置き換えて,スピングラス理論の手法を用いて解析しています.詳細は記事を参照してください.
ジャミング転移
ジャミング転移は,近年統計物理学で注目されるようになった相転移現象の一つです.これは,粒子を空間に詰め込んだときに起こる相転移です.粒子の密度が小さいときは粒子が自由に動けるので系は流体のように振る舞い,密度が大きいときは粒子が動けなくなり固体のように振る舞います.この流体から固体への変化は急激に起こります.
例えば砂時計では,砂山の表面では砂が動けるので落ちてきた砂が流れるように動きますが,砂山の内部では密度が高く砂の位置は固定されており,固体のように振る舞います.
ジャミング転移を研究するモデルとして用いられているのが,球のパッキング問題です.これは,球状の粒子を箱に密度を変えながらランダムに詰め込んだときの系の振る舞いを調べる問題であり,相転移点や臨界現象が特定されています.
背景のまとめ
統計物理学の様々な概念を紹介したところで,再び本研究の問題設定と貢献について説明します.
まず,相転移現象は普遍性クラスに分類できることを説明しましたが,球のパッキング問題の臨界現象がどれだけ普遍的なのかは明らかになっていません.そこで,他にもジャミング現象を示す問題のクラスはあるのかということが興味の対象となります.また,球のパッキングと同じ普遍性クラスに属するが,球のパッキングよりも単純で扱いやすい系が見つかれば,その単純な系を詳しく調べることでジャミング現象についての理解が深まることが期待されます.
次に,離散変数 CSP が相転移現象を示すことを説明しました.一方で,連続変数 CSP についてはあまり研究がなされていないのが現状です.連続変数 CSP は離散変数 CSP と同様に相転移現象を示すのか,示すならば,どのような普遍性クラスに属するのか,という点の解明が求められます.
本研究は,以上2つの問題について考えます.具体的には,パーセプトロンというシンプルな連続変数の CSP の SAT-UNSAT 転移を解析し,これが球のパッキングのジャミング転移と同じ普遍性クラスに属することを示します.
手法と結果
パーセプトロンの定式化
パーセプトロンは,以下のような問題です.
- パラメータ $\vec{X} \in \mathbb{R}^N$ と,与えられた $M$ 個のパターン $\vec{\xi^\mu} \in \mathbb{R}^N , (\mu=1,\dots,M)$ との内積を定数 $\kappa$ 以上にできるか?
この問題を, $N$ 変数 $M$ 制約のCSPとして以下のように定式化できます.
- 次の制約を満たす $\vec{X} \in \mathbb{R}^N$ を求めよ
- 制約:
$$\vec{X} \cdot \vec{X}=N \ r_\mu\equiv\frac{1}{\sqrt{N}} \vec{X} \cdot \vec{\xi^\mu} – \kappa \geq 0,,(\mu=1,2,\dots,M)$$
$r_\mu$ をギャップと呼びます.
この問題は, $\kappa$ の符号によって性質が大きく異なります.
($\kappa \geq 0$ のとき)
パーセプトロンは2値分類問題と見なせます.2値分類問題とは, $M$ 個のデータからなるデータセット ${(\vec{x^\mu}, y^\mu) \mid \mu=1,2,\dots,M} , (\vec{x^\mu} \in \mathbb{R}^N, y^\mu \in {+1, -1})$ が与えられたときに, $y^\mu=+1$ なら $\vec{w} \cdot \vec{x^\mu} \gt 0$, $y^\mu=-1$ なら $\vec{w} \cdot \vec{x^\mu} \lt 0$ となるようなパラメータ $\vec{w} \in \mathbb{R}^N$ を求める問題です. $\vec{\xi^\mu}=y^\mu \vec{x^\mu}$ としてパーセプトロン問題を解いたときの解 $\vec{X}$ は2値分類問題の解 $\vec{w}$ になっています.
また, $\kappa \geq 0$ のときパーセプトロン問題は凸になっています.つまり,2つの解を取ったときに,それらの中間もまた解になっています.凸最適化問題は簡単なアルゴリズムで解くことができます.
($\kappa < 0$ のとき)
この問題は非凸になっています.つまり,2つの解の中間が解になっているとは限りません.一般に,非凸な問題の最適解を求めることは困難です.
統計力学模型への変換
次に,パーセプトロン問題を統計力学模型のエネルギーの最小値を求める問題に帰着させます.制約がすべて充足されていればエネルギーが $0$,充足されていない制約が存在すればエネルギーが正となるようなハミルトニアンを設計すればよいです.
制約1つのエネルギーを
$$v(r) = \frac{1}{2}r^2 \theta(-r)$$
とします.ここで, $\theta(x)$ はステップ関数 ($x\geq 0$ で $1$, $x<0$ で $0$) です. $v(r)$ のグラフは以下のようになります.

図2: エネルギーのグラフ
全体のエネルギーは,各制約のエネルギーの総和とします $$H[\vec{X}]=\displaystyle \sum_{\mu=1}^M v(r_\mu)$$
$H[\vec{X}]=0$ であることと, $\vec{X}$ がパーセプトロン問題の解であることは同値です.これにより,パーセプトロンの充足可能性を調べることは, $H[\vec{X}]$ の基底エネルギーを調べることに帰着します.
調べる物理量
基底エネルギー
前節で説明したように,基底エネルギーを調べることはパーセプトロンの充足可能性を調べることに対応します.また,パラメータ数とパターン数の比 $\alpha := M/N$ や $\kappa$ の値を固定し,ランダムなパターンに対する基底エネルギーの平均値を求めることで,SAT-UNSAT 転移を捉えることができます.基底エネルギーの平均値が $0$ であれば,その $(\alpha,\kappa)$ の組はSAT相にあり,基底エネルギーの平均値が $0$ より大きければ,その $(\alpha,\kappa)$ の組はUNSAT相にあるということになります.
ギャップの分布 $g(r)$
基底エネルギーの他にも,SAT-UNSAT転移点付近での系の振る舞い,すなわち臨界現象に興味があります.それらを特徴づける物理量をいくつか調べます.
一つはギャップの分布です. $r_\mu\geq 0$ のとき, $r_\mu$ の値は制約 $\mu$ がどれだけ余裕を持って充足されているかを表します.ギャップの分布 $g(r)$ とは, $M$ 個の制約のうち,ギャップが $r$ となるものの割合を表します.
球のパッキング問題では, $r$ が小さい領域では $g(r)$ がべき乗則 $g(r) \propto r^{-\gamma}$ に従うことが知られており,臨界指数 $\gamma \approx 0.413$ が報告されています.パーセプトロンの場合も $g(r)$ はべき乗則に従うのか調べ,そうならば臨界指数の値を特定することが目標です.
力の分布 $P(F)$
ギャップの分布が,充足されている制約に関する量であるのに対し,力の分布は,充足されていない制約に関する量です.
充足されていない,すなわち $r_\mu \lt 0$ である各制約は,その制約を満たす方向にパラメータ $\vec{X}$ を動かそうとする力を及ぼします.ハミルトニアン $H$ が $r_\mu$ の2次式になっていることから,制約 $\mu$ が $\vec{X}$ に及ぼす力 $F_\mu$ は $\vert r_\mu \vert$ に比例します.よって,力の強さは,制約がどれくらいの強さで違反されているかを表します.力の分布 $P(F)$ は, $M$ 個の制約のうち,力の大きさが $F$ となるものの割合を表します.
球のパッキング問題における力の分布は,ギャップの分布と同様に, $F$ が小さい領域でべき乗則 $P(F) \propto F^\theta$ に従い,臨界指数 $\theta \approx 0.423$ が報告されています.そこで,パーセプトロンの力の分布はどのように振る舞うのかを本論文では解析します.
計算方法
$\alpha = M/N$ と $\kappa$ の値を固定して, パターン ${\vec{\xi}^\mu}_{\mu=1,2,\dots,M}$ を Gauss 分布に従ってランダムに生成したときの,パーセプトロンの各物理量の平均値を調べます.
計算にはレプリカ法を用います. $\kappa \geq 0$ については先行研究 [2] がありますが,本論文では $\kappa < 0$ の領域も解析します.
計算の流れは以下のとおりです.
- RS 仮定 (レプリカ対称性が破れていない,すなわち解空間で状態は一つしかないと仮定) で計算する
- RS 解が不安定になる領域を求める
- RS 解が不安定になる領域で, RSB 仮定 (レプリカ対称性が破れている,すなわち解空間で状態は複数に分裂しているという仮定) で計算する
計算の詳細は論文を参照してください.
計算結果
以下のような相図が得られました.
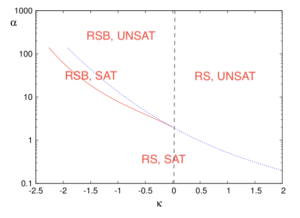
図3: パーセプトロンの相図 (https://iopscience.iop.org/article/10.1088/1751-8113/49/14/145001)

青線は SAT-UNSAT 転移点を表しており,青線の下側では SAT, 上側では UNSAT となります.
赤線は,RS 解が不安定になる dAT (de Almeida-Thouless) 線を表しています.赤線の下側では RS 解は安定であり,パーセプトロンの解の存在領域は連結です.赤線の上側では RS 解は不安定であり,解の存在領域は細かく分裂します.なお,レプリカ対称性の破れが起こるのは $\kappa \lt 0$ の領域のみであり, $\kappa \geq 0$ ではすべての $\alpha$ でRS解が安定です.これは, $\kappa \geq 0$ ではパーセプトロンの解が凸であることからもわかります.
次に, SAT-UNSAT 転移点における臨界現象を調べました. $\kappa \geq 0$ の領域では,臨界現象は起こりませんでした.すなわち,ギャップの分布 $g(r)$ や力の分布 $P(F)$ はべき乗則に従いませんでした.一方で, $\kappa \lt 0$ の領域では臨界現象が起こり, $r$ が小さい領域で $g(r) \propto r^{-\gamma}, , \gamma \approx 0.413, , P(F) \propto F^{\theta}, , \theta \approx 0.423$ がわかりました.これらの値は,球のパッキングのジャミング転移における臨界指数と一致します.この発見より,パーセプトロンは $\kappa \lt 0$ で球のパッキングと同じ普遍性クラスに属することがわかりました.
結論
本研究では,連続変数 CSP の最も単純な例の一つであるパーセプトロンを解析しました.その結果, $\kappa \lt 0$ の非凸領域では,臨界現象が見られ,球のパッキングと同じ普遍性クラスに属することがわかりました.
球のパッキングよりもシンプルで解析しやすい模型であるパーセプトロンがジャミング転移と同じような相転移を示すことが明らかになったことにより,パーセプトロンの性質を更に調べることでジャミング転移に対するさらなる知見が得られることが期待されます.
また,この結果より,他の多くの非凸な連続変数 CSP も同じ普遍性クラスに属することが予想されます.他の連続変数 CSP に対しても,本研究のような解析を行うことで,この予想を検証することが求められます.
あとがき
レプリカ法の計算を追うのが大変でした (まだ一部追い切れていません).
この研究では,パーセプトロンの解を求めるアルゴリズムについては触れられていません.特に,解の凸性が失われ,レプリカ対称性が破れる領域では,既存のアルゴリズムでは解くことが難しくなることが予想されます.K-SAT の場合は,スピングラス理論の手法を転用して,RSB 領域でも効率的なアルゴリズムが構成できましたが,パーセプトロンに対しても同様のアプローチができるのかは気になるところです.
また,多層パーセプトロンの場合で解析することも面白そうだと思います.多層パーセプトロンの解空間の構造に対する知見が得られれば,現代の深層学習の成功を説明する手がかりになるかもしれません.
参考文献
[1] Mezard, M., & Zecchina, R. (2002). The random K-satisfiability problem: from an analytic solution to an efficient algorithm. https://doi.org/10.1103/PhysRevE.66.056126
[2] Gardner, E., & Derrida, B. (1988). Optimal storage properties of neural network models. Journal of Physics A: Mathematical and General, 21(1), 271–284. https://doi.org/10.1088/0305-4470/21/1/031