文献情報

• タイトル：Exploration of new chemical materials using black-box optimization with the D-wave quantum annealer
• 著者：Mikiya Doi et al.
• 書誌情報：10.3389/fcomp.2023.1286226

概要

マテリアルズ・インフォマティクスにおいて、所望の物性値を持つ材料の組合せを高速に探索することが求められています。しかし、材料の組合せ数は膨大であり、物性値の計算(評価)にも時間的・金銭的コストが掛かることが一般的です。ブラックボックス最適化では、出来るだけ少ない評価数で所望の組合せを得ることを目指します。一方で、物性値が高いほど良い訳でもなく、合成のしやすさも重要な指標になっています。そこで本研究では、モデルのパラメータをサンプリングする際に分散を調整することで、多様な材料の組合せを得る手法を提案しています。それにより、物性値の高い様々な材料の組合せを得られることが示されました。

問題設定

本論文では、物性値の高い「置換基」の組合せを求めることを目的としています。置換基とは、有機化合物の水素原子を他の原子(団)に置き換えた化合物における、水素に置き換わった原子(団)のことです。置換基の例を図1に示します。

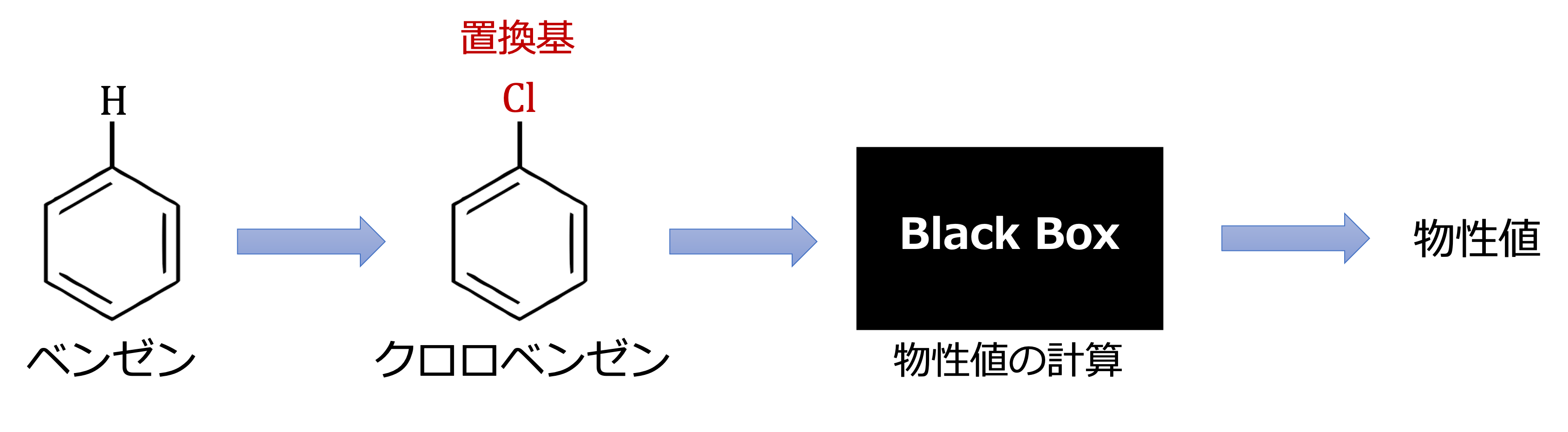
図1: 置換基と物性値計算(ブラックボックス)の例

ベンゼンの水素原子が塩素原子に置き換わった結果、クロロベンゼンに変化しています。この塩素原子のことを置換基と呼びます。本研究では置換基の結合部位の数を4つとし、R1, R2, R3, R4と呼ぶことにします。各部位に結合できる置換基の種類はそれぞれ、R1: 6個, R2: 29個, R3: 64個, R4: 64個あります。従って、置換基の組合せ総数は、6×29×64×64=712,704となります。ここで、R1は6種類ありますが、置換基を0からナンバリングすると0番目~5番目となります。D-Waveマシンはバイナリ変数しか扱えないため、このナンバリングを2進数に変換する必要があります。つまり、R1の5番目の置換基は２進数で(1, 0, 1)と表されます。R2 ~ R4に関しても同様に表記し、それらを連結したベクトルが解になります。
例えば、R1: 0番目, R2: 2番目, R3: 10番目, R4: 63番目 という組合せの場合、

$$
\vec{x} = (0, 0, 0,| 0, 0, 0, 1, 0,| 0, 0, 1, 0, 1, 0,| 1, 1, 1, 1, 1, 1)
$$

と表記します。ここで、各置換基の数を表すのに必要なビット数は、R1: 3個, R2: 5個, R3: 6個, R4: 6個です。この置換基の組合せ$\vec{x}$を評価した時の物性値$y$が出来るだけ高くなるような組合せを発見することが本研究の目的です。しかし、実際に化合物を生成したり、それを評価するための計算には時間的にも金銭的にもコストが掛かります。そのため、何度もトライアンドエラーを繰り返すことは出来ません。そこで、ブラックボックス最適化を使用し、少ない試行回数で高い物性値を持つ組合せを得ることを目指します。

手法

D-Waveマシンを利用したブラックボックス最適化の詳細については、こちらをご覧ください。本記事では式の導出は省略し、具体的なアルゴリズムのみを紹介します。まず、代理関数を以下のように定義します。

$$
\begin{equation}
\begin{split}
f_{surrogate}(\vec{x}) &= \alpha_{0} + \sum_{i}\alpha_{i} x_{i} + \sum_{i<j}\alpha_{ij}x_{i}x_{j} \\
&=\vec{\alpha}^\mathsf{T}\vec{X}
\end{split}
\end{equation}
$$

ここで、

$$
\vec{X}:=\left(1, x_{1}, x_{2}, \ldots, x_{N}, x_{1} x_{2}, x_{1} x_{3}, \ldots, x_{N-1} x_{N}\right)^\mathsf{T}
$$

と定義しています。ここからは、$\min f_{surrogate}(\vec{x})$の解の物性値が高くなるような$\vec{\alpha}$を推定していきます。MAP推定を利用すると、以下の式が得られます。

$$
\vec{\alpha} = \underset{\vec{\alpha}}{\arg \max } \{ \log{P(\vec{y}|\vec{\alpha}, X)} + P(\vec{\alpha}) \}
$$

ここで、事前確率と事後確率は多次元ガウス分布を用いて以下のように定義します。
$$
\begin{equation}
\begin{split}
P(\vec{\alpha}) = \mathcal{N} (\vec{0}, \sigma_{\alpha}^2I)\\
P(\vec{y}|\vec{\alpha}, X) = \mathcal{N} (X\vec{\alpha}, \sigma_{y}^2I)
\end{split}
\end{equation}
$$

これらをMAP推定の式に代入し、$\vec{\alpha}$で微分すると、事後確率が最大となる$\vec{\alpha}$は次のように計算出来ます。

$$
\vec{\hat{{\alpha}}} = (X^{T}X + \lambda I)^{-1} X^{T} \vec{y}
$$

この$\vec{\hat{{\alpha}}}$は、損失関数の傾きが0となる点です。単純に物性値が最も高くなるような組合せを求めたいのであれば、$\vec{\hat{{\alpha}}}$を採用するのが好ましいと考えられます。しかし、実際には物性値は高いものの生成するのが難しい組合せも存在します。そこで、本研究では、$\vec{\hat{{\alpha}}}$から少しズレた値を採用します。そのズレ具合を制御するパラメータが分散$\sigma^2$です。つまり、$\vec{\alpha}$は以下の分布からサンプリングされると考えます。

$$
\begin{equation}
\begin{split}\vec{\alpha}|\vec{y}, X {\sim} \mathcal{N} (\vec{\mu}, \Sigma)\\
\vec{\mu} = (X^{T}X + \lambda I)^{-1} X^{T} \vec{y}\\
\Sigma = \sigma^2(X^{T}X + \lambda I)^{-1}\\
s.t \quad \sigma^2 = \sigma_{y}^{2}, \lambda = \sigma_{y}^{2} / \sigma_{\alpha}^{2}
\end{split}
\end{equation}
$$

これより、ブラックボックス最適化は以下の手順で行われます。

1. $\vec{\alpha}$をサンプリングする。
2. $\vec{\alpha}$をQUBO行列に変換し、D-Waveマシンでサンプリングする。
3. サンプリングされた解候補の中で、エネルギーの低い上位10個の解を取り出す。その際、既にデータセットに存在する解は除外する。
4. 取り出した解の物性値を計算する。
5. 解とその物性値をデータセットに加え、step1に戻る。

上記のサイクルを、ここからはループと呼ぶことにします。

結果

まずは、$\sigma^2$を変化させた時の置換基のヒストグラムを図2に示します。$\sigma^2=0$の時は、R4の15番目の置換基が頻繁に現れるといった、ヒストグラムの偏りが生じています。一方で、$\sigma^2=12 \times 10^{-3}$のように分散を大きくすると、様々な置換基の組合せが得られていることが分かります。

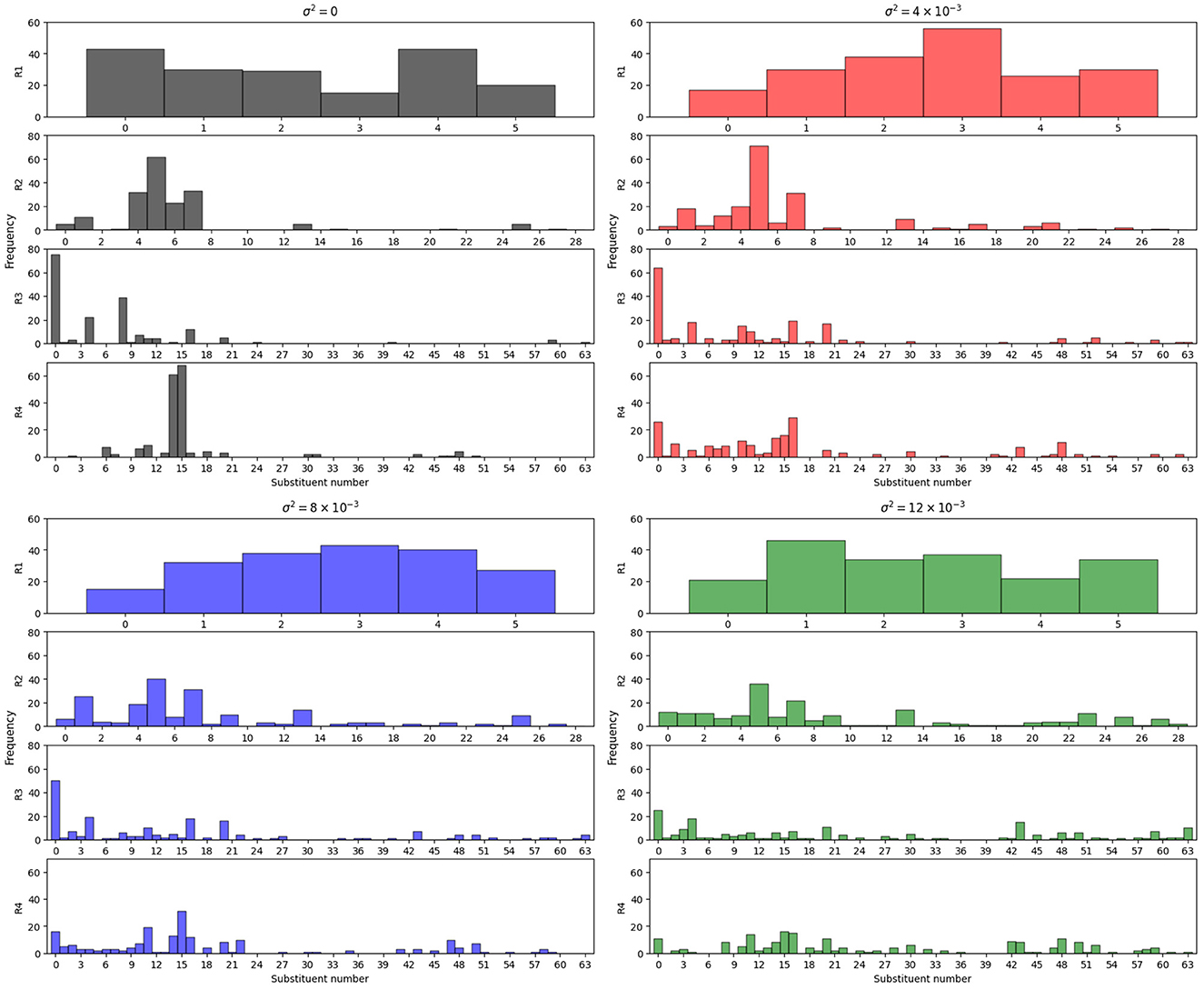
図2: $\sigma^2$を変化させた時の置換基のヒストグラム

次に、ループ数と代理モデルの決定係数$R^2$の関係を表しています。決定係数は、モデルの予測がどの程度実際のデータを正確に説明しているかを示す指標で、1に近いほどモデルがデータに良くフィットしていることを意味します。$R^2$は初期データセットの992点と、各ループで追加されるサンプル点を考慮して計算されています。図3では、$\sigma^2$が大きくなるにつれて$R^2$が小さくなる傾向が見られます。これは、多様な入力ベクトルやその評価値を適合させる必要があるからだと考えられます。

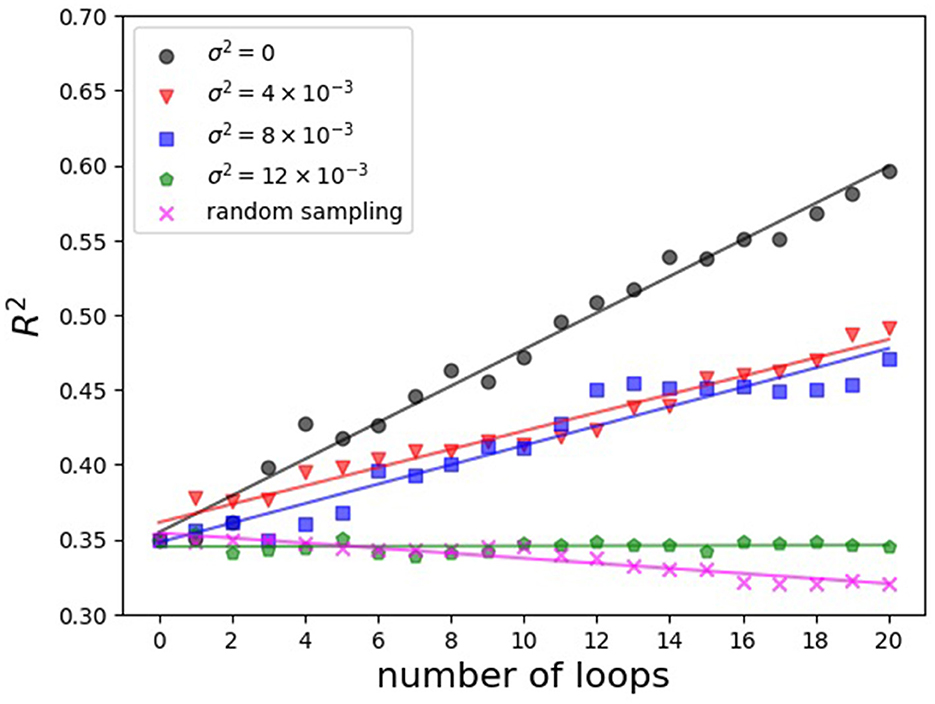
図3: ループ数と決定係数$R^2$の関係

図4では、ループ数と物性値の最高値の関係をプロットしています。$\sigma^2=0$の場合、少ない試行回数で物性値の高い組合せが得られていることが分かります。一方で、$\sigma^2$が大きくなるにつれ、物性値の高い組合せは見つかりにくくなっていることが分かります。

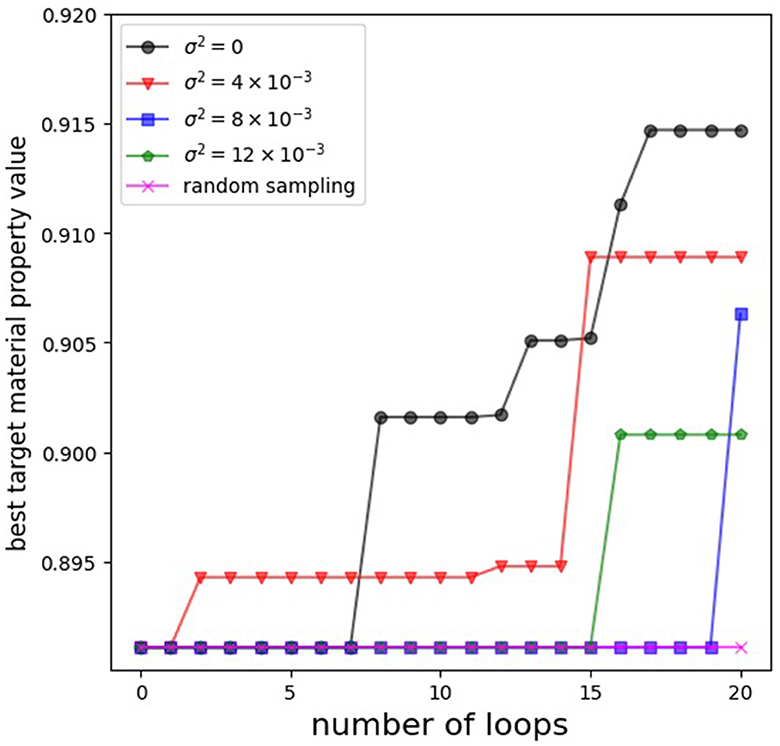
図4: ループ数と物性値の最高値の関係

続いて、初期データセットに含まれる置換基の組み合わせと、各実験の終了までにデータセットに追加された置換基の組み合わせに対する物性値のヒストグラムを図5に示します。赤い点線は、望ましい物性値として定義したカットオフ値（0.880）です。$\sigma^2=0$の場合、カットオフ値を超える組合せが多く得られていることが分かります。一方で、$\sigma^2$が大きい場合、物性値の高い組合せは得られにくくなっていることが分かります。

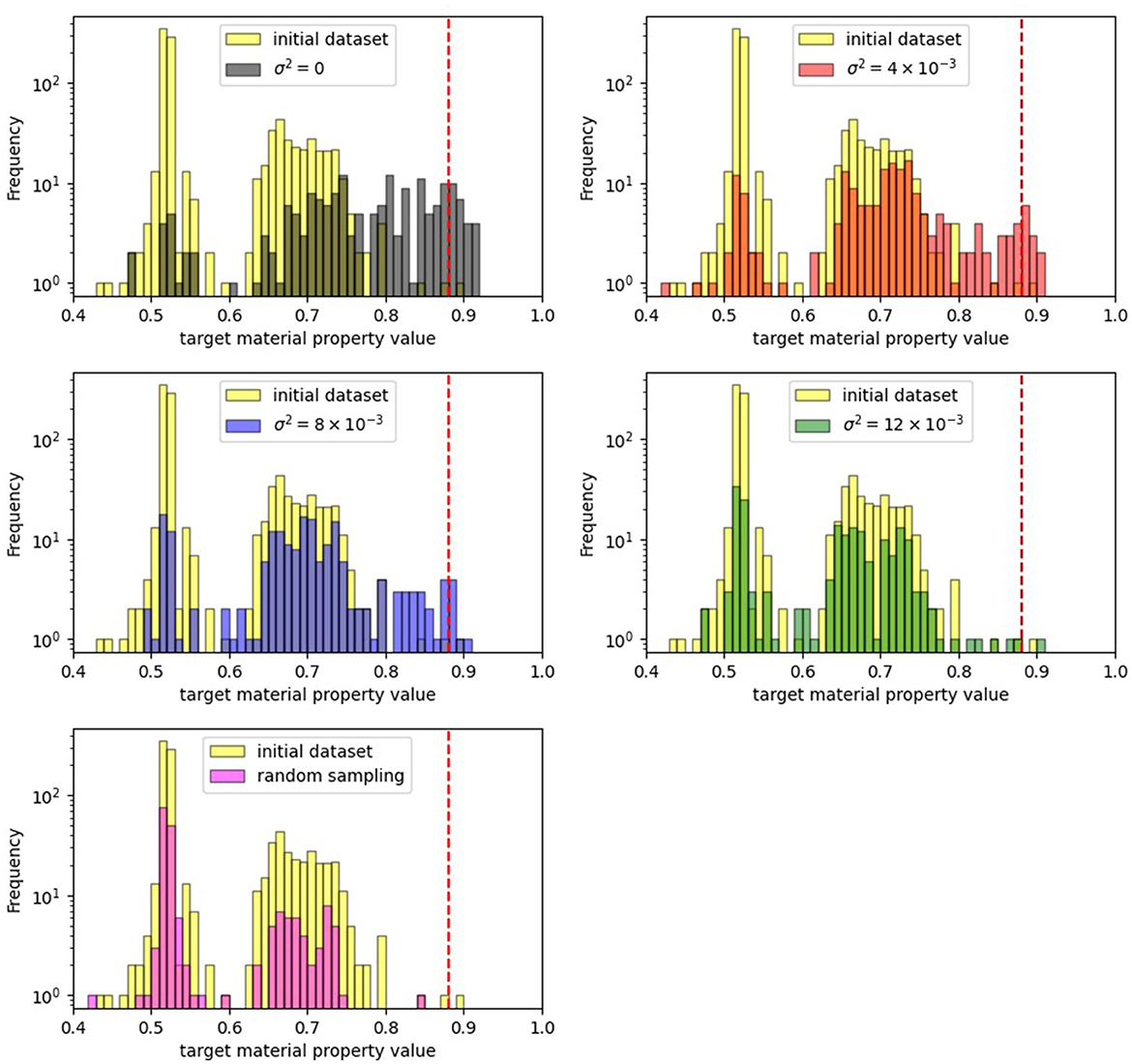
図5: 物性値のヒストグラム

最後に、目標物性値（0.880）を超えた置換基の組合せを表1・2に示します。$\sigma^2 = 0$の場合は、目標値を超えた組合せが25組あり最多となっています。一方で、R4において14番目や15番目の置換基ばかりが選ばれていることが分かります。$\sigma^2 = 4 \times 10^{-3}$の場合は、得られる組合せ数は減少するものの、R4に0番目の置換基を含む組合せが得られるといった組合せの多様性が確認出来ます。

表1: $\sigma^2 = 0$における、目標物性値を超えた置換基の組合せ

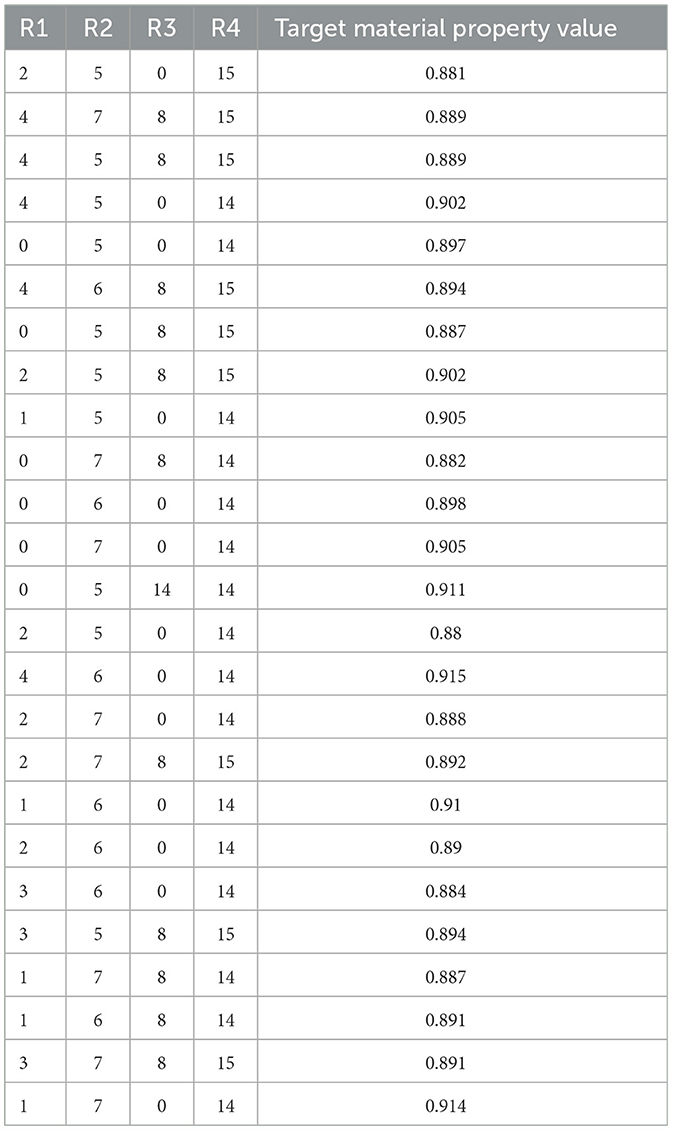
表2: $\sigma^2 = 4 \times 10^{-3}$における、目標物性値を超えた置換基の組合せ

考察

本実験は1インスタンスのみで行われているため、妥当性に議論の余地があります。しかし、量子アニーリングの利用により、望ましい物性値を持つ多様な組合せを効率的に発見出来ることを示しています。別のアプローチとして、シミュレーテッドアニーリングを使用して獲得関数を計算することを検討しています。今後の課題としては、シミュレーテッドアニーリングを使用した場合の性能や、量子アニーリングを用いた場合の計算時間の優位性を調査すると述べられています。

あとがき

本研究では、D-Waveマシンから得られた解の上位10個を新しいデータセットに追加していました。しかし、それらの解がどれだけバラついているのか、その中に最適解が含まれているのかどうかは不明でした。D-Waveマシンが最適解ではないものの、それに近い多様な解を出力することで探索の効率が高まっている、ということが示せると、D-Waveマシンの優位性が明らかになるのではないかと考えます。

本記事の作成者

鹿内怜央