量子アニーリングで人工素材を設計する “FMQA”

文献情報

タイトル：Designing metamaterials with quantum annealing and factorization machines
著者：Koki Kitai, Jiang Guo, Shenghong Ju, Shu Tanaka, Koji Tsuda, Junichiro Shiomi, Ryo Tamura
書誌情報：https://doi.org/10.1103/PhysRevResearch.2.013319

概要

$\def\argmin#1{\mathop{\rm arg~min}\nolimits #1}\def\R{\mathbb R}\def\N{\mathbb N}$近年、光の波長よりも細かなスケールで素材の構造を制御する技術が発展したことで、これまでの素材にはない特殊な性質を持った人工素材が設計できるようになってきました。これらの素材は「メタマテリアル」と呼ばれ、持続可能な社会を実現するためのエネルギー変換や環境浄化、医療などの分野での応用が期待されています。

メタマテリアルの設計においては、次の3つの要素が大きな役割を果たします。

光の波長よりも細かな構造を制御する技術
細かな構造を3次元的に積み重ねる技術
目的の性質を持つ素材の設計図を探す技術（自動材料発見技術）

本研究は3番目の要素に注目します。ここで問題となるのが、「目的の性質」をもつことが期待できる設計図の候補があまりにも多すぎることです。設計図の候補を一つ一つ虱潰しに調べ上げるのは現実的ではありません。そこで、本論文ではメタマテリアルの設計図を効率的に探すための手法として「ブラックボックス最適化」技術を用います。ブラックボックス最適化では、すでに性能がわかっている素材の設計図をもとに、より「優れた」設計図を探すための最適化問題を作成し、それを解くことで最適な設計図を探します。本研究では、この最適化問題を量子アニーリングを用いて解く試みを行います。

本論文では、量子アニーリングが自動材料発見技術に応用できることを示すために、特定の波長で熱の放射・吸収が行われる（波長選択型）ラジエーターに適した素材の設計図を探索します。数値実験の結果、人間が設計した従来の素材に比べて、量子アニーリングを用いた自動材料発見で作成した素材の方が、より高い性能を示すことがわかりました。このことから、量子アニーリングは自動材料発見技術に応用できる (かもしれない) ことが示されました。

背景と課題

次のように、制約条件 $g(\bm x) \leq 0$ の下で、コスト関数 $f(\bm x)$ を最も小さくするような組合せ $\bm x$ を求める問題を「組合せ最適化問題」といいます。

$$
\begin{aligned}
&\mathop{\rm minimize}\limits_{\bm x \in \{0, 1\}^N} && f(\bm x) \\
&\mathop{\rm subject\ to} && g(\bm x) \leq 0 \\
\end{aligned}
$$

組合せ最適化問題は、コスト関数 $f(\bm x)$ の評価（$f$ に具体的な値 $\bm x$ を入力して出力を計算する操作）に時間がかからない問題と、$f(\bm x)$ の評価に時間がかかる問題に大別することができます。これらはまったく異なるアプローチを取る必要があります。

評価に時間がかからない問題の場合、まずはその問題が、最大独立集合問題、巡回セールスマン問題、ナップサック問題などの有名な問題の形で定式化できるかを考えます。これらの有名な問題は研究の歴史が長く、厳密解法（時間はかかるが厳密な解を得る保証のある解法）や近似解法（比較的高速かつ、得られた解が厳密解からどれほど“離れている”かが保証されている解法）が知られています。

また、これらに対するメタヒューリスティクス（厳密な解を得る保証はないが、経験的に良い解を得られると知られている手法の総称）も研究されており、その一環として以下に示すQUBO (Quadratic Unconstrained Binary Optimization) の形式での定式化も考案されています [Lucas 2014; Glover et al. 2018]。

$$
\mathop{\rm minimize}\limits_{\bm x \in \{0, 1\}^N}
\quad
\bm x^\top \bm Q \bm x
$$

有名な解法に帰着できない場合には、遺伝的アルゴリズムやシミュレーテッドアニーリングなどといった古典的な「メタヒューリスティクス」を用いるか、その問題に適した新たな解法を作成することを考えます。

メタヒューリスティクスは通常、何度も $f(\bm x)$ を計算することで最適解を探索するため、コスト関数の評価に時間がかからない（$f(\bm x)$ の計算が一瞬で終わる）場合に有効です。ところが、現実世界での実験の結果得られる値をコスト関数の値とするもの や、シミュレーションの結果得られる値をコスト関数の値とするもの など、$f(\bm x)$ を評価するのに時間がかかる問題も世の中には存在します。

このように評価に時間がかかる（1分も2分もかかる）問題に対して古典的なメタヒューリスティクスを用いるのは現実的ではありません。そこで、別の角度での戦略が必要になります。

モデルベース戦略

本記事では、$f(\bm x)$ を計算するのに時間がかかる問題を「ブラックボックス最適化問題」と呼ぶことにします。ブラックボックス最適化問題に対しては「コスト関数の値の計算回数を減らす」ことが基本的な方針となります。そこでよく用いられるのが「モデルベース」なヒューリスティクス戦略です。

モデルベースな手法では、コスト関数 $f(\bm x)$ を直接最適化するのを諦め、代わりに「代理モデル」と呼ばれるモデルで近似しながら、以下の手順で間接的に最適化を行います。

Model-based Optimization
1. $t = b, b+1, \dots, B$ のあいだ繰り返す:
2. $\quad$ データ $\mathcal D=\{\bm x^{(i)}, y^{(i)}\}_{i=1}^t$ に代理モデル $\hat f$ をフィットさせる
3. $\quad$ 代理モデル $\hat f$ を用いて獲得関数 $\alpha(\bm x)$を作成
4. $\quad$ 獲得関数 $\alpha(\bm x)$ を最小化する入力値 $\bm x^{(t+1)} = \argmin_{\bm x} \alpha(\bm x)$ を探索
5. $\quad$ コスト関数の値 $y^{(t+1)} = f(\bm x^{(t+1)})$ を評価 (この計算は時間がかかると想定)
6. $\quad$ データセット $\mathcal D$ に $(\bm x^{(t+1)}, y^{(t+1)})$ を追加
7. 得られた最適な入力値 $\bm x^\ast = \argmin_{\bm x, y \in \mathcal D} y$ を出力

ここで、$b$ は初期データセット $\mathcal D=\{\bm x^{(i)}, y^{(i)}\}_{i=1}^b$ のデータ数、$B$ は終期データセット $\mathcal D=\{\bm x^{(i)}, y^{(i)}\}_{i=1}^B$ のデータ数です。$B$ は「予算 (budget)」とも呼ばれます。

組合せ構造をもつブラックボックス最適化問題にこのような戦略を用いる際に問題となるのが、獲得関数の最適化問題

$$
\mathop{\rm minimize}\limits_{\bm x \in \{0, 1\}^N} \quad \alpha(\bm x)
$$

に厳密解法を用いるのが現実的ではなくなることです。この場合、適切な近似解法やメタヒューリスティクスで解のサンプリングを行うことになります。本論文では、メタヒューリスティクスの1種である量子アニーリング (Quantum Annealing; QA) によって解をサンプリングする方法が提案されています。

手法: 量子アニーリングを用いたブラックボックス最適化 (FMQA)

本論文では、獲得関数 $\alpha(\bm x)$ を以下の QUBO の形で記述し、D-Wave社 (2020年当時) の量子アニーリングマシンである D-Wave 2000Q を用いて解をサンプリングします。

$$
\begin{aligned}
&\mathop{\rm minimize}\limits_{\bm x \in \{0, 1\}^N}
&& \alpha(\bm x) = \sum_{i, j = 1}^N Q_{ij} x_i x_j
\end{aligned}
$$

ここで $\bm x \in \{0, 1\}^N$ は $N$ 次元のベクトルで、各要素は $0$ または $1$ の値をとります。$\bm Q = [Q_{ij}] \in \R^{N \times N}$ は $N$ 行 $N$ 列の行列で、各要素は実数値をとります。

代理モデル

本論文では、代理モデルの学習に使用できるデータ数を増やすためには、評価に時間のかかる目的関数 $f$ をある $\bm x$ で評価して、$(\bm x, y=f(\bm x))$ のペアをデータセットに追加する必要があります。このような設定では、できるだけ少数のデータ数を元に、目的関数をうまく近似できるような代理モデルが望ましいです。

Factorization Machines (FM): 以上のような要望を満たすモデルとして、本論文では「Factorization Machines (FM)」[Rendle 2010] というモデルに着目します。FM は以下の形式で書かれる回帰モデルです。

$$
\begin{aligned}
f_\mathrm{FM}(\bm x ; b, \bm w, \bm V)
&= b + \sum_{i=1}^N w_i x_i + \sum_{i,j: i \lt j} \bm v_i^\top \bm v_j x_i x_j \\
&= b + \sum_{i=1}^N w_i x_i + \sum_{i=1}^{N-1} \sum_{j=i+1}^N \sum_{k=1}^K v_{ik} v_{jk} x_i x_j
\end{aligned}
$$

$b \in \R, \bm w \in \R^N, \bm V \in \R^{N \times K}$ はパラメータで、$K \in \N$ はハイパーパラメータです。

FM は、相互作用項 $x_i x_j$ の係数が「隠れベクトル」と呼ばれるベクトル $\bm v_i$ と $\bm v_j$ の内積 $\bm v_i^\top \bm v_j$ で書かれているのが特徴です。これにより、モデルパラメータの個数は

$$
p = \underbrace{1}_{b} + \underbrace{N}_{w} + \underbrace{ KN }_{\bm v} =\mathcal{O}(KN)
$$

に抑えることができます。このように、FMはパラメータ数の増大が線形オーダーであるという強みを持っているのが特徴です。

一方、比較のために、例えば次式で与えられる2次多項式

$$
\begin{aligned}
f_{\mathrm{poly}2}(\bm x ; b, \bm w, \bm W)
&= b + \sum_{i=1}^N w_i x_i + \sum_{i,j: i \lt j} w_{ij} x_i x_j
\end{aligned}
$$

を見てみると、モデルパラメータの個数は

$$
p = \underbrace{1}_{b} + \underbrace{N}_{w} + \underbrace{ \frac{1}{2} N (N-1) }_{\bm v} =\mathcal{O}(N^2)
$$

となり、変数の個数 $N$ の平方のオーダーで増加することがわかります。

本論文でのFM: 本論文では定数項 $b$ は無視し、さらに相互作用項において $i \lt j$ で和を取る部分を、すべての $i$ と $j$ で和を取るように変更していますが、この変更によってモデルの性質が根本的に変わることはありません。

$$ \begin{aligned} \hat f_\mathrm{FM}(\bm x ; \bm w, \bm V) &= \sum_{i=1}^N w_i x_i + \sum_{i=1}^{N} \sum_{j=1}^N \sum_{k=1}^K v_{ik} v_{jk} x_i x_j \end{aligned} $$

このFMの1回の計算量は、数式通りに計算した場合には $\mathcal O(KN^2)$ ですが、相互作用項に対し次のような変形を行うことで $\mathcal O(KN)$ に削減することができます。

$$
\begin{aligned}
\sum_{i=1}^{N} \sum_{j=1}^N \sum_{k=1}^K v_{ik} v_{jk} x_i x_j
&= \sum_{k=1}^K \left( \sum_{i=1}^{N} \sum_{j=1}^N v_{ik} v_{jk} x_i x_j \right) \\
&= \sum_{k=1}^K \left( \sum_{i=1}^{N} v_{ik} x_i \sum_{j=1}^N v_{jk} x_j \right) \\
&= \sum_{k=1}^K \left( \sum_{i=1}^{N} v_{ik} x_i \right)^2
\end{aligned}
$$

また、各 $x_i$ が $0$ または $1$ の値を取ると指定した場合、$x_i^2 = x_i$ が常に成り立つので、このモデルは次のように書き直すこともできます。

$$
\begin{aligned}
\hat f_\mathrm{FM}(\bm x ; \bm w, \bm V)
&= \bm x^\top \left( \mathop{\rm diag}[\bm w] + \bm V^\top \bm V \right) \bm x
\end{aligned}
$$

ただし

$$
\bm V
= [\bm v_1, \bm v_2, \dots, \bm v_N]
=\begin{bmatrix}
v_{11} & v_{21} & \cdots & v_{N1} \\
v_{12} & v_{22} & \cdots & v_{N2} \\
\vdots & \vdots & \ddots & \vdots \\
v_{1K} & v_{2K} & \cdots & v_{NK}
\end{bmatrix}
\in \R^{K \times N}
$$

です。したがってこのモデルは、QUBO形式の目的関数

$$ f(\bm x) = \bm x^\top \bm Q \bm x $$

における行列 $\bm Q$ をランク $K$ で低ランク近似しているとみなすことができます。

本論文ではこのモデルを、各ステップでデータセット $\mathcal D$ を用いて勾配法で訓練します。以上のような FM を代理モデルに使用し、QA で解のサンプリングを行うことから、本手法は FMQA と名付けられています。

獲得関数

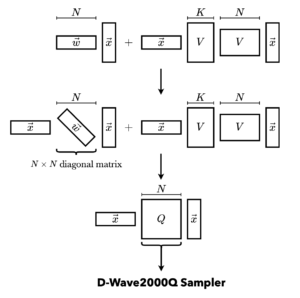
FMQAの獲得関数の模式図。論文を元に記事作成者が作成。

FMQA で用いる獲得関数は代理モデルと同一のものです。ただし、D-Wave 2000Q で解をサンプリングするために、FM を QUBO の形に書き直します。

$$ \begin{aligned} f_\mathrm{FM}(\bm x ; \bm w, \bm V) &= \sum_{i=1}^N w_i x_i + \sum_{i=1}^{N} \sum_{j=1}^N \sum_{k=1}^K v_{ik} v_{jk} x_i x_j \\ &= \sum_{i=1}^{N} \sum_{j=1}^N Q_{ij} x_i x_j \\ &= \alpha(\bm x) \end{aligned} $$

ただし

$$ \begin{aligned} Q_{ij} &= \left\{\begin{aligned} & \sum_{k=1}^K (v_{ik})^2 + w_i && (i=j) \\ & \sum_{k=1}^K v_{ik} v_{jk} && (i \ne j) \end{aligned}\right. \end{aligned} $$

このようにして作成された QUBO を dwave.embedding.chimera.find_clique_embedding メソッド [document] を用いてキメラグラフ上に埋め込み、D-Wave 2000Q に送信します。D-Wave 2000Q の制約上、この方式で埋め込むことができる全結合グラフの頂点数は63頂点に限定されるため、最大問題サイズも $N=63$ に限定されることになります。

FMQAのまとめ

以上をまとめると、FMQAは以下のようなアルゴリズムになります。

FMQA: Black-box optimization using FM and QA
1. $t = b, b+1, \dots, B$ のあいだ繰り返す:
2. FMのパラメータを、データ $\mathcal D=\{\bm x^{(i)}, y^{(i)}\}_{i=1}^t$ を用いて勾配法で訓練する
3. FM を最小化する入力値 $\bm x^{(t+1)} = \argmin_{\bm x} \hat f_{\mathrm{FM}}(\bm x)$ を探索
4. コスト関数の値 $y^{(t+1)} = f(\bm x^{(t+1)})$ を評価 (この計算は時間がかかると想定)
5. データセット $\mathcal D$ に $(\bm x^{(t+1)}, y^{(t+1)})$ を追加
6. 得られた最適な入力値 $\bm x^\ast = \argmin_{\bm x, y \in \mathcal D} y$ を出力

実験1: 予備実験

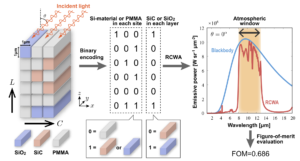
本実験の全体図。元論文より引用。

ここからは論文内の実験結果を説明します。実験設定や変数の設定方法などは別の記事で説明する予定です。ここでの結果を見るために押さえておくべき点は以下の4点です。

FOM (Figure of Merit) と呼ばれる材料の “よさ” の最大化を目的とする
FOMは設計された素材と、特定の波長領域での黒体との “近さ” と “遠さ” を測るもので、理論上の最小値は $-1$、最大値は $1$ である (ただし $\mathrm{FOM} = 1$ が実現できるとは限らない)
より具体的には、放射強度 (電磁放射の強さ、黒体のときに最大となる) が、波長域 $8-13~\mathrm{\mu m}$ 領域で黒体に近く、それ以外の領域でほぼ $0$ になるように設計
変数の個数 $N$ は、材料の “横向き” のグリッド数 $C$ と、“縦向き” のグリッド数 $L$ を用いて $N = L\times(C+1)$ で表される
材料は “横向き” に繰り返される・・・つまり、$C=8$ では $C=4$ のものと同一の構造を作成することも可能

FMが材料探索に利用できることの確認

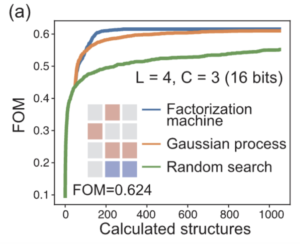
FM、ガウス過程、ランダムサーチの3手法の比較。元論文より引用。初期データの個数は50個。初期データを変化させながら16インスタンス実行した平均のみを記載。元論文より引用。

まず、本論文で用いた代理モデルである FM が自動材料探索のためのモデルとして有用であることを実証するために、初期データとして 50 点をランダムに与えたあと、FM、ガウス過程 (Gaussian process)、およびランダムサーチ (random search) でブラックボックス最適化を行い、結果を比較します。

この実験では問題の変数を $16$ としているため、理論上存在する設計図は $2^{16} = 65,536$ 通りです。この程度の個数であれば、代理モデル $\hat f$ に対して全探索を行っても、現在のコンピュータでも現実的な時間で解を求めることができます。そのため、今回の実験では、フィッティングした回帰モデルを最大化 (あるいは最小化) する入力 $\bm x$ を全探索により発見してデータセットに加えています。

結果、繰り返し回数の上限に達した時点で、FOMの大きい順にFM、ガウス過程、ランダムサーチと並びました。中でも FM を用いた場合には、300ステップ以内に実際に最も良い設計図を見つけることができています。このことは、FM が材料探索の問題において有用であることを示唆しています。

QAがブラックボックス最適化の内部ソルバに使えることの実証

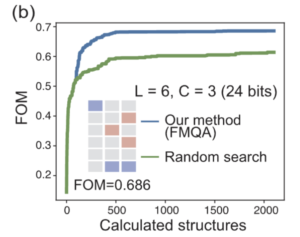
FMQAとランダムサーチの比較。元論文より引用。初期データの個数は50個。初期データを変化させながら16インスタンス実行した平均のみを記載。

FMが材料探索に有効であることは分かりました。続いて、より高次元の設定の場合に、QAを用いても良い性能を出せるか確認する必要があります。FMQAがランダムサーチを上回る結果を出すことを確認することで、少なくとも無情報でのランダムウォークを行うようなアルゴリズムではないと言えるはずです。そこで、ここでは全探索による最適化は非現実的となるような、理論上存在する設計図が $2^{24} = 16,777,216$ 通りの設定を用いて、FMQAを用いたものと、ランダムサーチを用いたもので比較を行っています。

結果、この問題設定では FMQA がランダムサーチを上回っているため、FMQA は完全にランダムに探索するよりも賢い手法であることがわかります。少なくとも QA が原因でランダムサーチよりも性能が低下するというような事態にはなっていないことが分かります。

最適な構造の探索

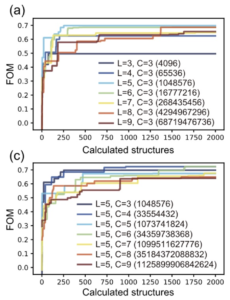
最大FOMを、シミュレーションした設計図の個数の関数として表示。元論文より引用。(a) $C=3$ に固定し、$L$ を変化させて材料探索を行った結果、(b) $L=5$ に固定し、$C$ を変化させて材料探索を行った結果。

最大FOMを、シミュレーションした設計図の個数の関数として表示。元論文より引用。(a) $C=3$ に固定し、$L$ を変化させて材料探索を行った結果、(c) $L=5$ に固定し、$C$ を変化させて材料探索を行った結果。

ここまでで FMQA が材料探索において有用な手法であることがわかったので、D-Wave 2000Q が取り扱い可能な範囲で $L$ と $C$ を変化させながら材料探索を実行することで、小規模な範囲での最適FOMの探索を行います。図 (a) では $L$、すなわち層の数を変化させながら実験を行っています。また図 (c) では $C$ すなわち設計図の周期を変化させています。

ここで、$(L,C) = (5,4)$ の場合と $(L,C) = (5,8)$ の場合を比較すると、$(L,C) = (5,4)$ のほうがFOMが大きくなっています。もしも両方の実験において厳密に最も良い構造が得られていると仮定するならば、これは不自然です。なぜなら、設計された素材の構造は $x$ 方向に繰り返すと仮定しているため、$(L,C) = (5,4)$ で良い構造が得られているならば、それを単に $x$ 方向に2回繰り返して得られる $(L,C) = (5,8)$ の構造は、同じくらい良い構造と評価されるはずだからです。

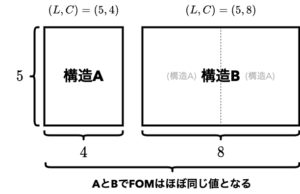
にも関わらず、同じくらい良い解が得られていないということは、単に $x$ 方向に2回繰り返しただけの構造が発見できていないことを示唆しています。したがって、実際には、現在の条件 (最大で2000ステップ) においては、最も良い構造は発見できていないということになります。

実際、グラフ (c) で $(L,C) = (5,4)$ (青) と $(L,C) = (5,8)$ (オレンジ) の曲線をよく見てみると、前者の場合は 1000 ステップ程度でFOMがある程度収束しているように見えますが、後者の場合は2000ステップ時点では若干右肩上がりであるように見えます。確かに、2000ステップ程度では最も良い構造を発見できていないという主張は成立しそうです。

以上のことは、より大規模な設定で最適構造を探索するには、より探索ステップ数を増やしたり、より効果的なFMの訓練アルゴリズムを使用しなければならないことを意味しています。

本実験: 最適構造の探索

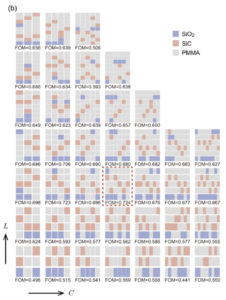
各 $(L,C)$ の組に対し、材料探索により発見された設計図を可視化。元論文より引用。各行は $L$ を、各列は $C$ を表す。

この図は、様々な $(L, C)$ の組に対し、FMQAで探索を行って得られた最適構造を示しています。この内、赤の破線で囲まれた $(L,C) = (5,6)$ は、FOMが最も大きくなったものです。このとき $\mathrm{FOM} = 0.724$ で、本論文によれば、この値は従来の人間が手探りで設計して得られたFOMよりも大きな値です。このことから、FMQAは人間よりも優れた性能をもつ材料探索機であるといえます。

ところで、上図において灰色の部分は、“PMMA” (ポリメタクリル酸メチル、アクリルガラスと呼ばれる透明なプラスチックで、アクリル板や眼鏡のレンズなど幅広く用いられる) が使用されていることを意味しています。$L=5$ を超える多層構造において実験の範囲内で得られた最適構造を見ると、PMMAだけで構成された層が多くあることが分かります。大規模なメタマテリアルの設計においては、電磁波をほとんど透過する箇所が存在することが何らかの重要な役割を担っているのかもしれません。

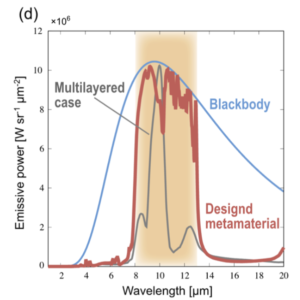
$L=5$、$C=6$ で最もFOMが高い設計構造について、RCWAによって計算された放射強度（赤線）、黒体放射強度（青線）、および $C=1$ として同様の探索を行った場合（灰色の線）の放射強度を波長の関数としてプロット。元論文より引用。

$L=5$、$C=6$ で最もFOMが高い設計構造について、RCWA (厳密結合波解析、周期的な構造を扱うためにフーリエ変換を用いてマクスウェル方程式の解を求める手法) によって計算された放射強度（赤線）、黒体放射強度（青線）、および $C=1$ として同様の探索を行った場合（灰色の線）の放射強度を波長の関数としてプロット。元論文より引用。

この図は、FOMが最大となった $(L, C) = (5, 6)$ における最適構造の放射強度を図示したものです。波長域 $8-13~\mathrm{\mu m}$ 領域では黒体に近く、それ以外の領域では放射強度がほぼ $0$ になるように設計できていることがわかります。

まとめ

この論文では、極めて多くの候補の中からシミュレーションによって最適な設計図を探索する「材料探索」に、Factorization Machines という回帰モデルと量子アニーリングマシンを組み合わせる新たなブラックボックス最適化手法、「FMQA」が提案されました。FMQAを熱波長選択型メタマテリアルの設計に用いたところ、最大FOMとして 0.724 という値を得ることができました。これは、従来人間が手探りで調査してきたFOMよりも大きな値です。以上のことから、FMQAは材料探索における新たな有用な手法の1つといえます。

また本論文は、イジングマシンをブラックボックス最適化に応用する初めての試みです。これまで量子アニーリングマシンは目的関数がQUBOで明確に定式化できる場合にのみ適用可能でした。本論文の結果は、QUBOの形式で表現できる代理モデルを導入することで、定式化が難しい問題にもイジングマシンを適用できる可能性を示しています。

あとがき

材料科学に関する論文のためか、専門用語が説明無しに登場するので読むのに大変苦労しましたが、ブラックボックス最適化の手法としてかなり興味をもって読むことができました。FMは勾配法による訓練が可能であり、大規模な問題に対しても並列処理などを駆使して代理モデルの訓練ができるのが1つのメリットではないかと思います。

しかし、量子アニーリングではなくシミュレーテッド・アニーリングやその他のメタヒューリスティクスを用いた場合についての性能評価はあまりしっかりと行われていなかったり、比較対象の「ガウス過程」という時にカーネル関数として何を用いたのか、ハイパーパラメータはどうしたのかなどの情報が欠落しているなど、最適化手法としては調べられる点が多くあるように思います。他のブラックボックス最適化の手法との比較も視野に入れながら調査を行っていくと、FMQAの特性についてもっとわかることがあるかもしれません。

今後はさらに、この手法がどのようなブラックボックス最適化手法に対して優れた性能を発揮するのか、また量子アニーラ以外のヒューリスティクスを応用できるかどうかなどについて調べると、より可能性が広がっていくのではないでしょうか。

本記事の作成者

森田圭祐

Post Views: 351