T-Wave開設以来、いくつかの先行研究や導入事例に関する記事が出ている中で、どのように具体的な問題をD-Waveマシンで解くのかということは皆さん気になっていると思います。本記事では グラフ分割問題 を例に、サポートツールであるqbsolvを用いてD-Waveマシンに解かせる過程を示します。
問題を解く過程の概略
一般的にqbsolvを用いてD-Waveマシンで、組合せ最適化を行う際に必要となるステップは以下の通りです。
Step 1. 問題のQUBO表現の確認(二値変数の意味、ハミルトニアンなど)
Step 2. QUBO行列$Q_{ij}$の要素の計算
Step 3. quboファイルの生成
Step 4. qbsolvコマンドの実行と結果の解釈
Step 1. グラフ分割問題のハミルトニアンの確認
グラフ中のノードを2つのグループに分割(最小カット)する場合には、あるノードが所属するグループを表す2値変数$s_i \in \{ -1, 1 \}$を考え、最小化すべきハミルトニアン(目的関数)は、
$$ \mathrm{Obj}(\mathbf{s}) = \sum_{(i, j) \in E} (s_i – s_j)^2 + \alpha \left( \sum_i s_i \right)^2 $$です。ここで、$E$はエッジの集合を表しており、$\sum_{(i, j) \in E}$はノード$i$とノード$j$がエッジ$(i, j)$で結ばれているような$i, j$の組について和を取るという意味です。
Step 2. QUBO行列の要素の計算
一般にQUBO形式の問題の目的関数は、
$$ \mathrm{Obj}(\mathbf{x}) = \sum_{i, j} Q_{ij} x_i x_j $$で与えられます。D-Waveマシンにおけるプログラミングとは、行列$Q_{ij}$の要素を問題に応じて与えることに他なりません。では、先ほどのグラフ分割に関する目的関数を元に行列$Q_{ij}$の要素を計算してみましょう。
最初に注意しなければならないのは、qbsolvコマンドを用いる際にはIsing表現 ($s_i \in \{-1, 1 \}$)ではなく、QUBO表現($x_i \in \{0, 1 \}$)で目的関数を記述しておく必要があり、従って、Step 1.で記述した目的関数を変数変換
$$ s_{i} = 2x_{i}-1 $$で変換して、式を展開していく必要があります。以後、順々に式変形のステップをご覧に入れます。
$$ \begin{aligned} \mathrm{Obj}(\mathbf{x}) &= \sum_{(i, j) \in E} ((2x_i – 1) – (2x_j-1))^2 + \alpha \left( \sum_i (2 x_i – 1) \right)^2 \\ &= \sum_{(i, j) \in E} 4(x_i – x_j)^2 + \alpha \left( \sum_i x_i – N \right) \left( \sum_j 2x_j – N\right) \\ &= \sum_{(i, j) \in E} 4 (x_i^2 + x_j^2 – 2x_i x_j) + \alpha \left[ \sum_i \sum_j 4 x_i x_j – 4N \sum_i x_i + N^2 \right] \end{aligned} $$となりますが、変数によらない定数和、および定数倍の部分は目的関数から除くことができます。また、0, 1の二値変数の場合、常に$x_i = x_i^2$が成り立ちますから、上の式の一次の項は$x_i = x_i^2$で書き直して、
$$ \mathrm{Obj}(\mathbf{x}) = \sum_{(i, j) \in E} (x_i^2 + x_j^2 – 2x_i x_j) + \alpha \left[ \sum_i \sum_j x_i x_j – N \sum_i x_i^2 \right] $$と書けます。
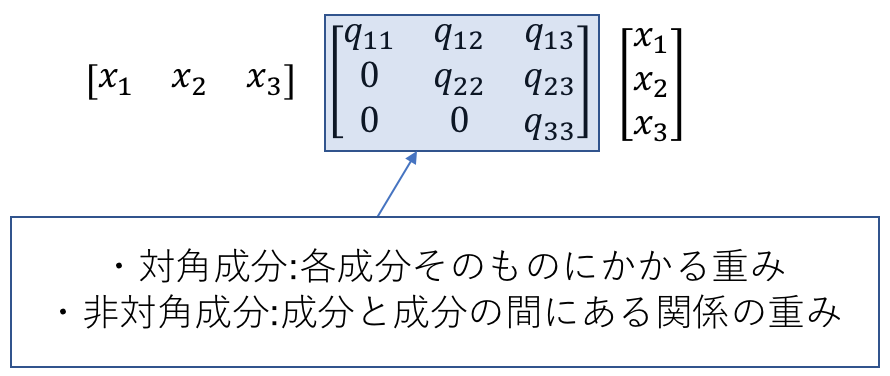
行列$Q$の要素は各二次式$x_i x_j$に付く係数でしたから、それぞれの$i, j$の組について、上の式を元に場合分けをして計算することになります。$Q_{ij}$を上式の第1項からなる成分$f_{ij}$と第2項からなる成分$g_{ij}$にわけて、それぞれ具体的に計算してみましょう。
$$ f_{ij} = \left\{ \begin{aligned} & d_i && \text{if $i = j$,} \\ & -2 && \text{if $i < j, (i,j) \in E$,} \\ & 0 && \text{otherwise} \end{aligned} \right. $$ここで$d_i$は頂点$i$から伸びる辺の数(次数)を表しています。この要素は目的関数の第1項の和に現れる$x_i^2$に起因します。$d_i = \sum_{(i, j) \in E} 1$であることからわかります。
$$ g_{ij} = \left\{ \begin{aligned} & \alpha (1 – N) && \text{if $i = j$,} \\ & 2 \alpha && \text{if $i < j$,} \\ & 0 && \text{otherwise} \end{aligned} \right. $$ここで、$f_{ij}, g_{ij}$が上三角行列になるように計算していますがこれは後述のQUBOファイルを作成するためのソフトウェア上の仕様と考えてください。
出来上がった行列は下図のような形となっているでしょう。
Step 3. QUBOファイルの作成
qbsolvコマンドを実行する際のQUBOファイルは以下の形式を取ります。
p qubo 0 [変数の数N] [非ゼロ対角成分数] [非ゼロ非対角成分数]
c コメント行は行頭にcとだけ記述
c 対角成分を先に書く
c [i] [i] [Qii]
0 0 -1
1 1 -2
c などのように
c 続いて非対角成分を記述
c [i] [j] [Qij]
c ここで必ずi < jでなくてはならない
0 1 100
3 6 49
c などのようにさて,ここからはPythonスクリプトを使ってQUBOファイルを作っていきます.まず,第一項のEを表現するためにどの点とどの点が繋がっているかを入力します.加えて,行列のサイズとnを調べるために点の数も入力します.ここでは点の数をnode,線の情報を始点と終点の情報を持ったm×2行列として表現しています.
行列要素の計算に関するPythonスクリプトを以下に示します。
N = 10 # ノード数
alpha = 100 # αの値を設定
edges = [[0, 1], [0, 4], [0, 5], [0, 7], [1, 2], [1, 5], [1, 7],
[2, 3], [2, 6], [2, 9], [3, 6], [3, 8], [3, 9],
[4, 5], [4, 7], [5, 6], [5, 7], [6, 8], [8, 9]] # エッジのリスト例
#行列の初期化
Q = [[0] * N] * N
# コスト項gij
for i in range(len(edges)):
x = edges[i][0]
y = edges[i][1]
Q[x][y] -= 2
Q[x][x] += 1
Q[y][y] += 1
# ペナルティ項
for i in range(len(edges)):
Q[i][i] += alpha * (1 - N)
for j in range(i + 1, len(edges)):
Q[i][j] += 2 * alpha今回はこのように表現しました.あとは,この行列をquboファイルに書き出すだけです.出来上がったファイルは以下の通りです。
p qubo 0 10 10 45
c diagonal (elements)
0 0 -896
1 1 -896
2 2 -896
3 3 -896
4 4 -897
5 5 -895
6 6 -896
7 7 -896
8 8 -897
9 9 -897
c off-diagonal (couplers)
0 1 198
0 2 200
0 3 200
0 4 198
0 5 198
: : :Step 4. qbsolvコマンドの実行と結果
QUBOファイルは前述のような書式でテキストファイルの形で保存し、qbsolvコマンドを
$ qbsolv -i [QUBOファイル名]の形で実行します。実際的にはqbsolvコマンドを用いてD-Waveマシンに接続するためには関連ツールであるdwコマンドなどを必要としますが、本記事では具体的なコマンドの使い方については触れません。
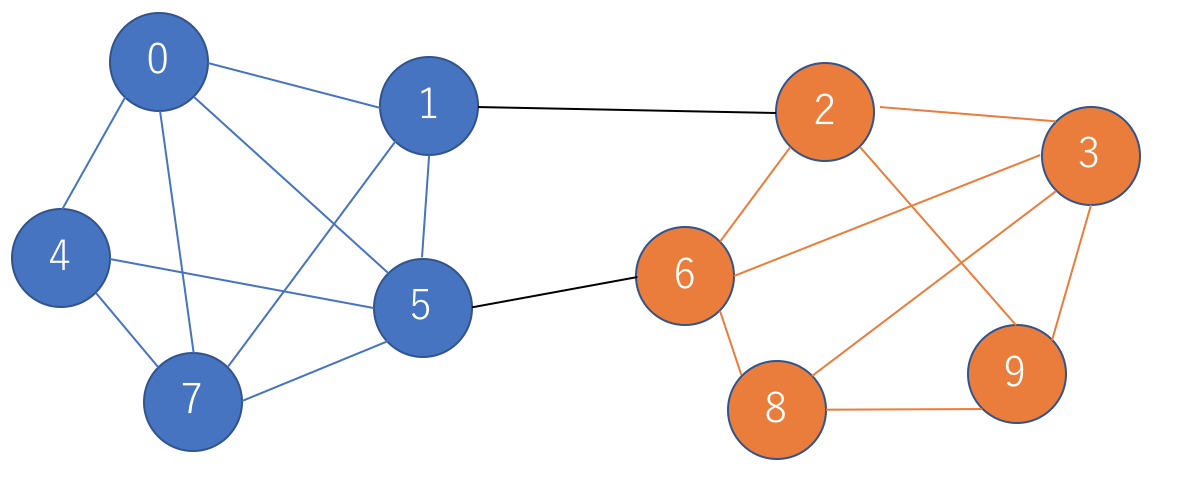
今回はこのグラフに対してグラフ分割を行います.
この場合では青のグループと赤のグループのつながりが強く,それを結ぶ2本の線を切って二分割することが正解です。
実際に先ほどのプログラムにグラフのデータを入力して、qbsolvを実行した結果、以下のような結果がターミナルプロンプトに出力されました。
$ qbsolv -i test.qubo
10 bits, Quantum solver, find Min, SubMatrix= 64, -a o, timeout=2592000.0 sec
1100110100
-2498.00000 Energy of solution
0 Number of Partitioned calls, 1 output sample
0.00044 seconds of classic cpu time3行目が結果の変数列で、左から,点0,1,2…に対応しており,0と1がどちらのグループに属するかを示しています。1で表されるグループは0,1,4,5,7であり図の青のグループに相当し、0で表されるグループは2.3,6,8,9で赤のグループに相当するので、正しく最小カットを選ぶようにグループ分けがされたことがわかります。
0.00045秒の部分は、qbsolvコマンドの内部処理にかかった時間であり、ターミナル上の実行時間は2.2秒程度でした。
まとめ
D-Waveマシンで問題を解くためには行列の要素の計算が難しいと感じました。行列の計算には二値関数の計算、和の展開、式の解釈など慣れないことが多く、途中何回も計算が合わずに間違った結果が返ってきました。D-Waveマシンを動かすことは大変でしたが正しい結果が返ってきたときの感動は言葉で表せないほど大きなものでした。そして、1度動かしてみて慣れてきたので2回目以降はそれほど苦労しないかなという印象です。これからは、qbsolv以外の方法でD-Waveマシンを動かす方法を学んだり、この問題以外の問題をD-Waveマシンで解いていこうと思います。
本記事の担当者
金垣 葵(編集:みやままさみち)