非負値行列分解 “Nonnegative/binary matrix factorization with a D-Wave quantum annealer” by Daniel O’Malley, et al. (2017)
本記事で紹介する論文では、D-Waveマシンを用いた量子アニーリングにより二値変数制約のついた 非負値行列分解 の手法と顔画像認識に応用した結果を示している。速度性能評価のために、古典的アルゴリズムを用いるGurobiとqbsolv(タブーサーチ)を用いた場合とD-Wave 2Xで得られた最適解に逹する累積TTT (time-to-target)を測り、そのアニーリング回数依存性を比較・検討している。 文献情報 Daniel O’Malley, Velimir V. Vesselinov, Boian S. Alexandrov, Ludmil B. Alexandrov, “Nonnegative/binary matrix factorization with a D-Wave quantum annealer”, arXiv:1704.01605. 非負値行列分解 (NMF)とは 非負値行列分解 (Nonnegative Matrix Factorization; NMF) は、$n \times m$行列$V$を全て非負値の要素からなる$n \times…
量子アニーリングで 迷路 から脱出する “Navigating a Maze using a Quantum Annealer” by Scott Pakin
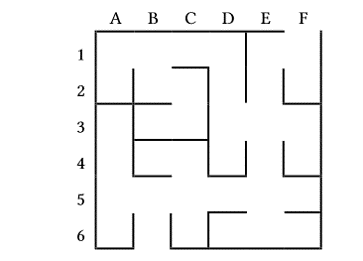
本記事で取り上げる論文では 迷路 における最短経路を求める問題をイジングスピングラスとして定式化し、D-Wave 2Xを用いて解いた結果を示している。補助ツールとして、問題を小問題に分割し、D-WaveマシンのキメラグラフにマップするQMASM(quantum macro assembler)を用いている。入出力やイジング模型へのマッピング、さらには 量子アニーリング にかかる時間のベンチマークや、そしてアニーリング時間による解の時間対精度などについても考察をしている。 文献情報 Scott Pakin, “Navigating a Maze using a Quantum Annealer”, Proceeding of PMES’17 Proceedings of the Second International Workshop on Post Moores Era Supercomputing, 30-36 (2017). 迷路の組合せ最適化問題としての定式化 迷路の定義と解の経路が満たすべき条件 本論文では、以下のような6×6のマスから構成…
グラフ分割問題 への応用 “Graph Partitioning using Quantum Annealing on the D-Wave System” by H. Ushijima-Mwesigawa, et al. (2017).
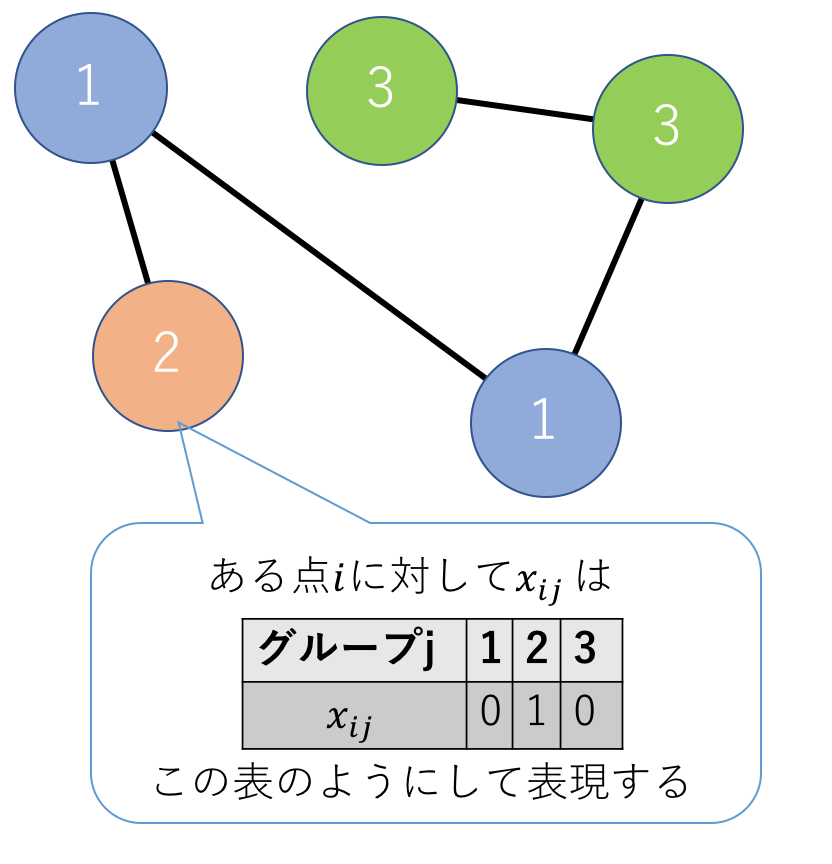
与えられたグラフを, 切断する辺の数を最小にしていくつかの部分グラフに分割する(最小カット問題) グラフ分割問題 をイジングスピングラス表現で定式化し, D-Wave 2Xにより解いた。グラフ分割問題 はKarpの21の組合せ最適化問題の1つとなっている。分割数が2の場合とそれ以上の数の場合では表現形式が異なることが興味深い。 文献情報 Hayato Ushijima-Mwesigwa, Christian F. A. Negre, Susan M. Mniszewski, “Graph Partitioning using Quantum Annealing on the D-Wave System”, arXiv:1705.03082 [quant-ph]. グラフ分割問題 本論文で扱う問題の定式化は, 分割数が2の場合とそれより大きい一般のKの場合でイジングスピングラス表現が少々異なる. 分割数が2の場合 最適化問題の定式化 分割数が2の場合, イジング表現(二値変数として+1か-1)で表現するのが自然である. 変数 $$s_i = \{ -1, 1 \}…
衝突回避のための最適な 航空経路選択 への応用 “Quantum Annealing Applied to De-Conflicting Optimal Trajectories for Air Traffic Management” by Tobias Stollenwerk et al. (2017).
文献情報 タイトル Quantum Annealing Applied to De-Conflicting Optimal Trajectories for Air Traffic Management 著者 Tobias Stollenwerk, Bryan O’Gorman, Davide Venturelli, Salvatore Mandra, Olga Rodionova, Hok K. Ng, Banavar Sridhar, Eleanor G. Rieffel, and Rupak BiswasarXiv:1711.04889 [quant-ph] 概要 大西洋横断飛行において、風に対する最適な軌道を採用することで生じるフライト間の衝突を、フライトの遅延によって回避するという問題がある。これをD-Wave 2XおよびD-Wave 2000Qを用いて解いた。 問題 航空における交通量は年々増加しており、使用可能な空域が限られてきている。大西洋に存在するジェット気流の影響を受ける大西洋横断飛行(NAT)において風に対する最適な軌道が採用されると、潜在的な衝突が発…
ジョブショップスケジューリング問題への応用 “Job Shop Scheduling Solver based on Quantum Annealing” by D. Venturelli, et al. (2015).
文献情報 概要 組合せ最適化問題の一つであるジョブショップスケジューリング問題を定式化し、これをD-Wave Twoにより解いた。 問題 ジョブショップスケジューリング問題(JSP:Job Shop Scheduling Problem)とは、機械を用いて複数のジョブを処理する場合に、全体の稼働時間やコストを最小にする問題である。各ジョブには複数のオペレーションが含まれ、各オペレーションには実行する機械に対して所要時間が決まっている。今回は以下の制約のもとで、オペレーションを機械に割り当てて、全てのジョブが完了するまでにかかる時間を最小化する。 最適化問題の定式化 組合せ最適化問題の種類: ジョブショップ・スケジューリング問題変数: $x_{i,t} \in \{0,1\}$ (オペレーション$O_i$が時刻$t$に始まるとき$1$, そうでなければ$0$)目的関数: $$ H_T(\bar{x}) = \eta h_1(\bar{x}) + \alpha h_2(\bar{x}) + \beta h_3(\bar{x}) $$ ただし、$\eta, \alpha, \beta >…
組合せ最適化問題のイジングモデル表現 “Ising formulations of many NP problems” by Andrew Lucas (2014)
文献情報 タイトル: Ising formulations of many NP problems 著者: Andrew Lucas (Google Scholar) 書誌情報: Frontiers in Physics 2, 5 (2014). (doi: 10.3389/fphy.2014.00005) 概要 近年、NP完全、あるいはNP困難な組合せ最適化問題の断熱量子最適化(AQO, Adiabatic Quantum Optimization)を用いた解法が注目されている。全ての組合せ最適化問題はIsingスピングラスの基底状態探索へと定式化することが可能であり、そのための手法としてAQOを用いる。 本論文では、組合せ最適化問題の累計パターンを集めたKarpの21のNP完全問題 (Karp’s 21 NP-complete problems)を含む組合せ最適化問題のIsingスピングラスによる定式化のハミルトニアンを網羅している。 取り扱われている組合せ最適化問題 分割問題 (Partitioning Problems) 数分割 (Number Parti…
最大クリーク問題への応用 “Finding Maximum Cliques on the D-Wave Quantum Annealer” by Guillaume Chapuis et al. (2018)
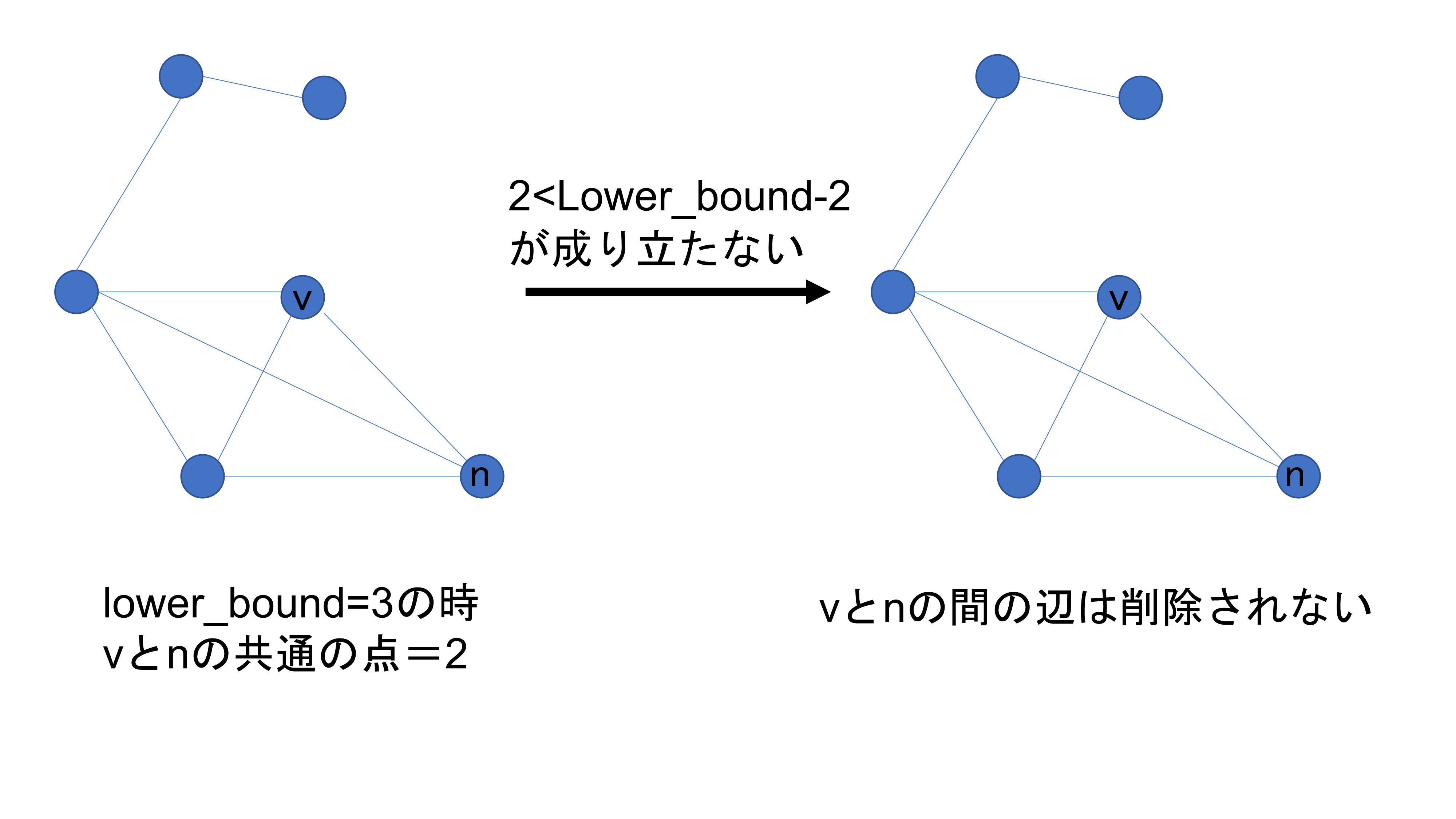
文献 概要 あるグラフの部分グラフのうち、それに含まれる任意の二点間に辺があるような部分グラフで最大のものを最大クリークと呼ぶ。与えられたグラフから最大クリークを発見する問題は最大クリーク問題と呼ばれており、これはNP困難であると知られている。本論文はこの最大クリーク問題のD-Wave 2Xを用いた解法について述べている。 解き方 グラフをG=(V, E)と表し、Vは点の集合、Eは辺の集合とする。グラフGに対して、辺のある二点間の辺をなくし、辺のない二点間に辺を張った(辺の集合Eに対して補集合$\overline{E}$を考える)グラフH=(V, $\overline{E}$)を考える。このとき、グラフHの独立集合S (どの二点間も辺で継がられてない点の集合)はグラフGではクリークに他ならない。つまり、最大クリーク問題と最大独立集合は表裏一体の関係となっており、このことを利用してグラフG最大クリークを求めるために、グラフHの最大独立集合問題を見つけることを試みる。この問題の読み替えは、のちで用いる変数の数や目的関数の表現をより簡便にする意味がある。 最適化問題の定式…
整数ナップサック問題のIsing表現ハミルトニアン:Knapsack with Integer Weights
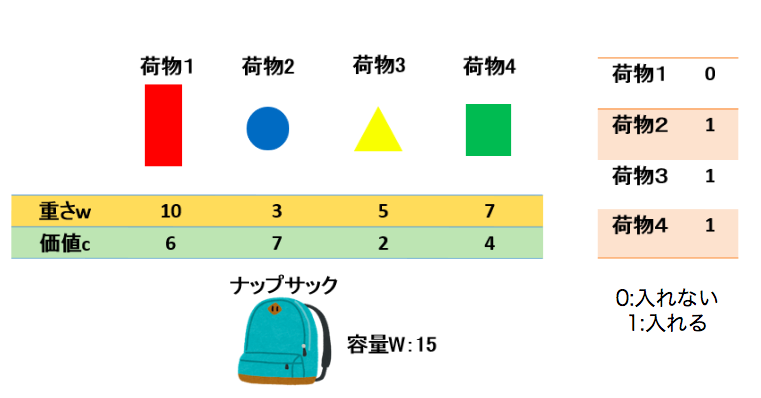
文献情報 概要 組合せ最適化問題の類型のひとつにナップサック問題がある。これをIsing模型(変数が1 or -1)と等価な形式であるQUBO形式(変数が1 or 0)によって表現した。 ナップサック問題とは 導入 ナップサック問題にはいくつかの種類があるが、今回扱うのは以下のような形式の問題である。 いま、N個の荷物(荷物1、荷物2、・・・荷物N)をがあり、それぞれの荷物についてその荷物の「重さ」と「価値」が分かっているとする。これらの荷物をナップサックに詰め込んで運びたいが、ナップサックには容量があるので持っていく荷物の重さの合計はこの容量を越えてはならない。この条件の下、持っていく荷物の価値の合計を可能な限り大きくするにはどの荷物を持っていくのが良いか? QUBO表現による定式化 適化変数: $x_{\alpha} \in \{0,1\}$ (荷物$\alpha$をナップサックに入れれば$1$,入れなければ$0$)補助変数: $y_n$ (自然数$m$を表すとき左から$m$番目の$y_m$が$1$,それ以外の全ての$y_{n (n\neq m)}$は$0$)目的関数: $$ \m…
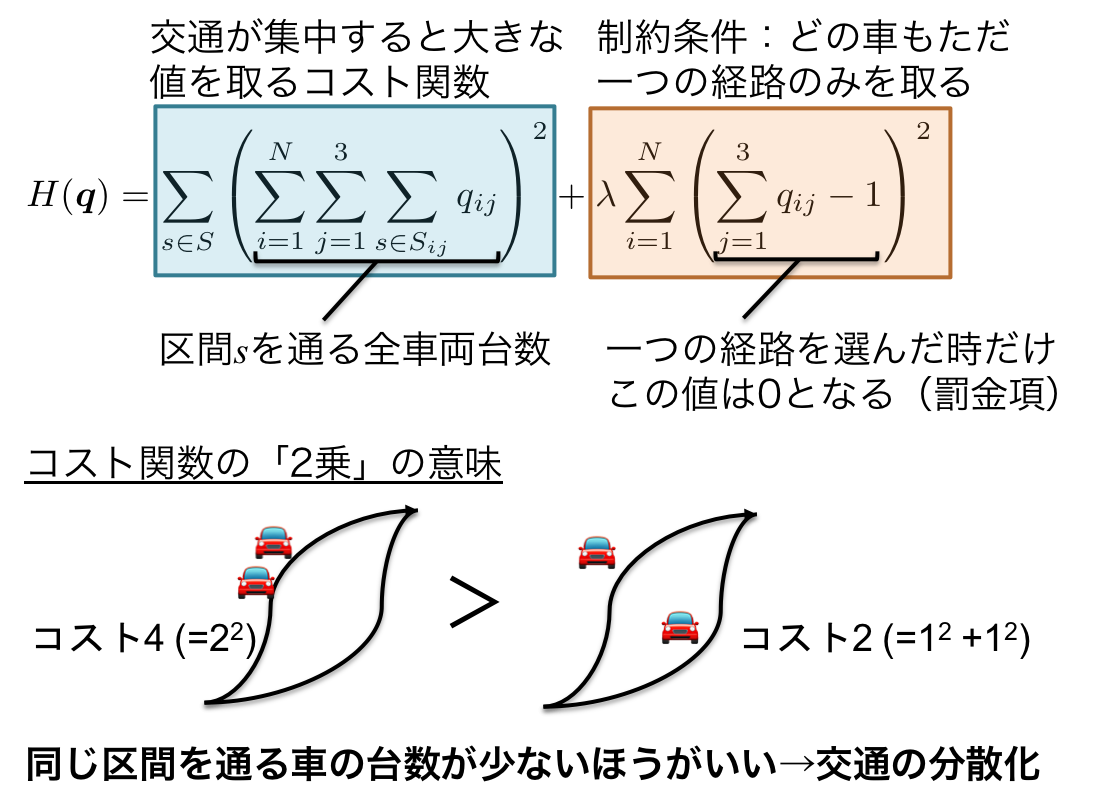
交通渋滞緩和のための経路選択への応用 “Traffic Flow Optimization Using a Quantum Annealer” by Florian Neukart, et al. (2017).
文献情報 概要 交通渋滞を緩和するために複数台の車の経路選択を組合せ最適化問題として定式化し、これをD-Wave 2Xにより解いた。 方法 方針 古典: 現時点の位置から目的地までの経路を各車両ごとに3つ用意する量子: 各車両の取る経路を目的関数を最小化するように選択する 最適化問題の定式化 組合せ最適化問題の種類: 二値整数線型計画問題変数: $q_{ij} \in \{0, 1\}$ (車$i$が経路 $j \in {1, 2, 3}$を取れば$1$, そうでなければ$0$)目的関数: $$ \mathrm{Obj} = \sum_{s\in S} \left( \sum_i \sum_j \sum_{s \in S_{ij}} q_{ij} \right)^2 + \lambda \sum_i \left( \sum_j q_{ij} – 1 \right)^2 $$ 用いたデータセット 公開データセットのT-Drive trajectory datasetの中から、北京の街の中心と北京空港の間を行き来する418台の車のGPSデータを今回の問題の対象として抽出した。ま…