量子アニーリングで車のCO2排出量を削減しよう!
渋滞を解消するような交通信号機の最適化は、ドライバーのストレス軽減やCO2削減量の削減という点において重要です。現在の日本では、定周期制御と交通感応制御という2つの方法を併用しています。交通感応制御ではリアルタイムに交通情報を取得し信号の状態を決定するため、高速な計算が求められており、量子アニーリングの活用が期待されています。量子アニーリングを活用したR. Shikanai らの先行研究では、曖昧なパラメタが存在し、モデル予測制御も導入されていません。本研究ではそのような曖昧なパラメータを除去し、モデル予測制御を組み込んだイジングモデルを提案します。
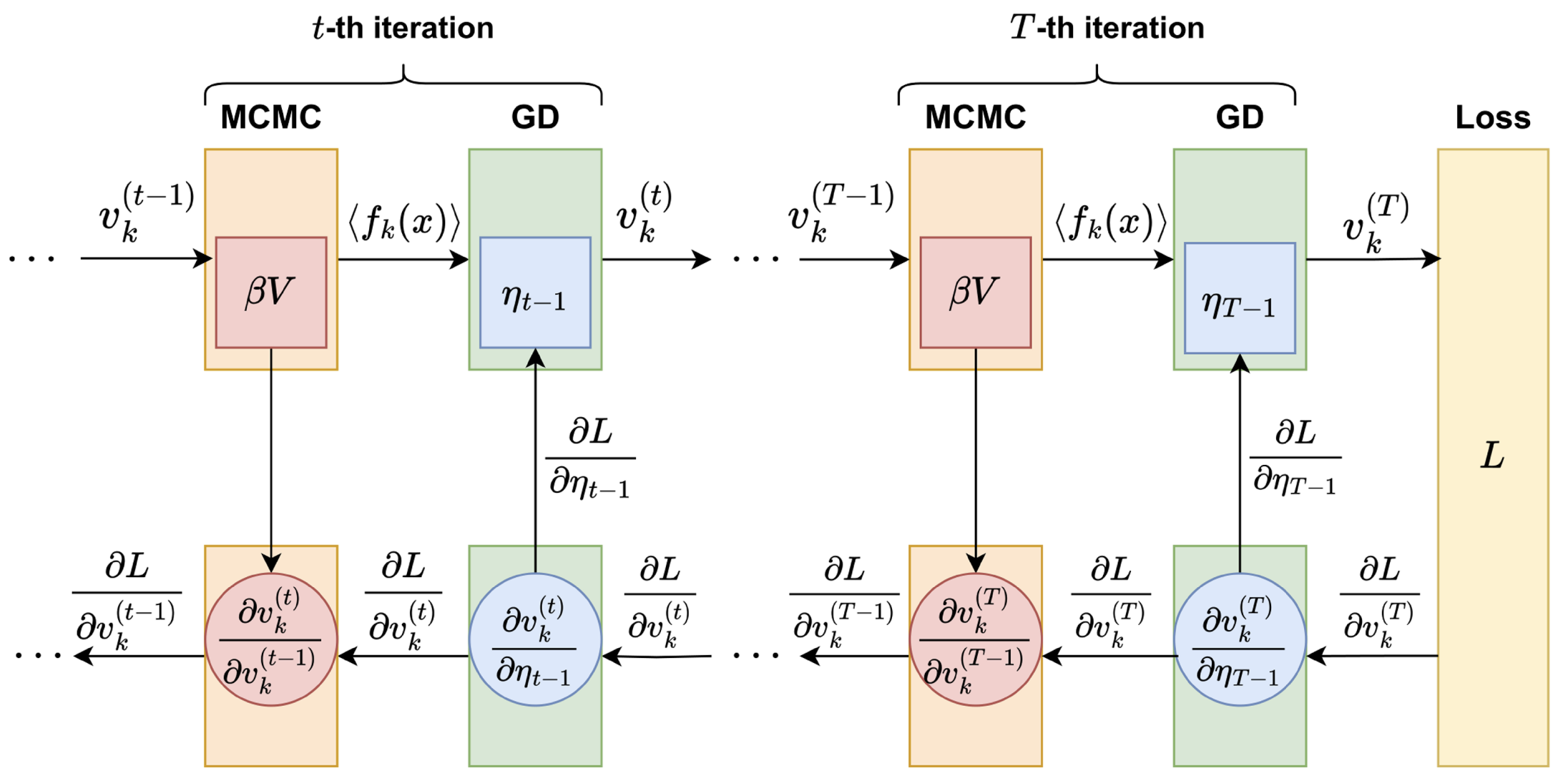
大関法に対する深層展開の適用
組合せ最適化問題の中には制約を持つ組合せ最適化問題が多く存在します。そのような制約付き最適化問題の解法として大関法と呼ばれる手法が知られています。大関法は、量子アニーリングやマルコフ連鎖モンテカルロ法のようなボルツマン分布からのサンプラーと勾配法を組み合わせた手法であり、サンプリングと勾配法によるボルツマン分布の更新を反復的に繰り返すアルゴリズムです。大関法によって得られる解の精度は、分布の更新の際に用いられるステップサイズと呼ばれるパラメータに大きく依存する一方、反復ごとのステップサイズの適切な調整は困難です。その問題に対処するために、本論文では深層展開と呼ばれる深層学習技術を大関法に適用しています。
量子アニーリングで電力ネットワークを最適化する
電力ネットワーク全体で電力を効率的に使用するためには電力の余剰の最適化が重要な要素です。本論文では、量子アニーリングを用いて電力余剰を最適に活用できるようなネットワークを探索する方法を示しました。そして、ドイツの送電ネットワークでの電力余剰を最適化するという問題に対して、量子と古典のハイブリッドソルバーと古典ソルバーのそれぞれで結果を出して、古典ソルバーに対して量子と古典のハイブリッドソルバーがコスト関数の値がより低い解を出すことを示しました。
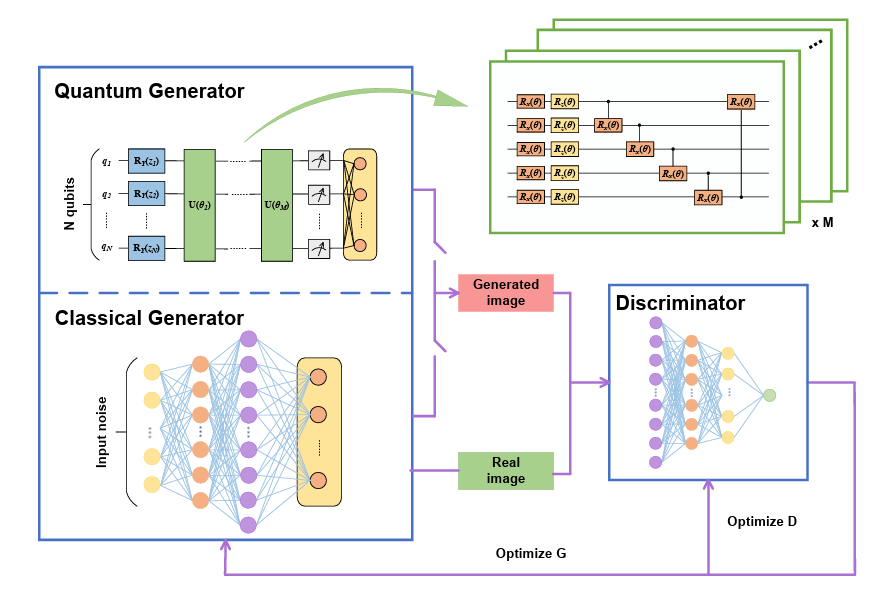
敵対的生成ネットワークの性能を高める変分量子回路
敵対的生成ネットワーク(GAN:Generative Adversarial Network)は、画像を生成する深層学習であり、パラメータが多くなるほど、計算コストが一層高くなるという問題があります。そこで、本論文ではGANの生成器を量子回路とニューラルネットワークのハイブリットで構成し、その結果、手書き画像の生成において、計算コストを削減することに成功しました。
制約付き量子アニーリング:罰金項を使わずにグラフ彩色問題を解く
量子アニーリングでは、組合せ最適化問題の制約は罰金項として表現することが一般的です。しかしこの手法は量子アニーリング (QA) の性能を落としてしまうことが知られています。本論文では 制約付き量子アニーリング (Constrained Quantum Annealing, CQA) と呼ばれる手法を用いて組合せ最適化問題を解きます。この手法は制約を罰金項として表現するのではなく、量子効果を表す driver Hamiltonian を適切に用いることで制約を満たした解のみに限定して探索を行うことができる手法です。本論文では組合せ最適化問題の一例としてグラフ彩色問題に注目して、グラフ彩色問題を CQA を用いて解きます。実験の結果では CQA により最適解に近い解を得ることができました。一方で予想と違う結果も得られ、この考察も行います。
無限幅ニューラルネットワークの統計力学 ― 活性化関数の観点から
ニューラルネットワーク(NN)の性能と活性化関数の関係にまつわる2つの研究の流れがあります.1つは,記憶容量の問題の統計力学的解析です.記憶容量とは,二値分類モデルが記憶できるランダムなデータの最大数(パラメータあたり)で,モデルの表現能力の指標の一つです.もう1つは,無限幅NNとGauss過程の関連に関するものです.この研究の流れは,NNの高い性能に対してより深い洞察を与える理論として注目されています.これらの研究は独立に発展してきましたが,両者には深いつながりがあることを指摘します.
量子アニーリングで人工素材を設計する “FMQA”
持続可能な社会を実現するためのエネルギー変換や環境浄化、医療などの分野での応用が期待されている「メタマテリアル」の設計図を効率的に探すための手法として「ブラックボックス最適化」技術を用いることが提案されています。ブラックボックス最適化では、すでに性能がわかっている素材の設計図をもとに、より「優れた」設計図を探すための最適化問題を作成し、それを解くことで最適な設計図を探します。本論文では、この最適化問題を量子アニーリングを用いて解く試みを行います。
D-Waveマシンを利用した材料探索
マテリアルズ・インフォマティクスにおいて、所望の物性値を持つ材料の組合せを高速に探索することが求められています。しかし、材料の組合せ数は膨大であり、物性値の計算(評価)にも時間的・金銭的コストが掛かることが一般的です。ブラックボックス最適化では、出来るだけ少ない評価数で所望の組合せを得ることを目指します。一方で、物性値が高いほど良い訳でもなく、合成のしやすさも重要な指標になっています。そこで本研究では、モデルのパラメータをサンプリングする際に分散を調整することで、多様な材料の組合せを得る手法を提案しています。それにより、物性値の高い様々な組合せを得られることが示されました。
パーセプトロンのジャミング転移
統計力学と組合せ最適化の関連は長らく指摘されています.特に,充足可能性問題 (SAT) やグラフ彩色問題などの,離散変数の 制約充足問題 (Constraint Satisfaction Problem, 以下 CSP) に対しては,統計物理学の観点からの研究が進んでいます.一方で,連続変数 CSP に対する統計力学的な研究はあまりなされていません.本論文では,ガラスのモデルとして統計物理学で研究されている「球のパッキング」問題が,連続変数 CSP として捉えられることに着目します.球のパッキングは「ジャミング転移」と呼ばれる相転移現象を示すことが知られています.本論文では,連続変数 CSP の単純な例であるパーセプトロンの挙動を統計力学の手法を用いて解析し,球のパッキングと同様のジャミング転移が起こることを示します.
D-Waveマシンの3世代間比較
2023年5月31日をもって、約5年間利用されてきたD-Wave 2000Qが廃止となりました。現在はD-Wave Advantage、そして2023-2024年に発売予定のD-Wave Advantage2のプロトタイプが利用可能です。本論文では、最大クリーク問題、最大カット問題を解くことにより、これら3世代のマシンの性能比較を行っています。その結果、最新のAdvantage2が、最適解に近い解を得られる確率において最も優れていることが分かりました。これはハードウェアグラフが密になり、マイナー埋め込みに必要なチェーンが少なくなったことが一因と考えられます。また、Advantage2では、比較的フェアサンプリングしていないことも分かりました。