本論文では量子アニーリングを用いた新たな作曲手法を提案します。音楽を構成する要素をメロディ・リズム・ハーモニーの３つに分け、それぞれに対して D-Wave マシンを用いた生成方法を示します。本記事では ｢ メロディ ｣ の生成に関する説明を行います。

本論文では、ボルツマンマシンの学習内のサンプリングにD-Waveマシンを用いることで、その画像生成の品質向上を目的としています。
分類器としてニューラルネットワークを予め学習しておき、特定の数字の画像を生成したときに、その画像の分類結果を測ることで直接的な評価を行います。

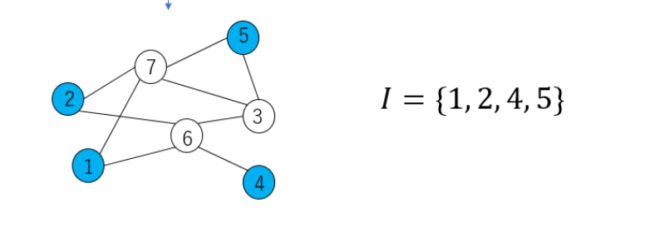
本記事では独立点集合を求める3つの近似的なアルゴリズムRamsey、CliqueRemoval、SampleISを説明します。

グラフ彩色とは隣接した頂点対を異なる色になるように彩色することです。3色以上のグラフ彩色はNP困難であり、高速に計算することが困難な問題の一つです。したがって、厳密性を犠牲にした近似的な解を求めるのが妥当であると考えられています。近似解を求める方法の一つにグラフから独立点集合(どの頂点も隣接していない頂点の集合)を求め、一つの独立点集合ごとに1色ずつ割り当てる貪欲法があります。本論文では、このアルゴリズムでグラフ彩色を行うときに独立点集合を量子アニーリングを用いて求めます。この提案手法を古典コンピュータで独立点集合を求めたときの結果を比較します。

ボルツマン機械学習では対数尤度関数を最大化するために、ギブス・ボルツマン分布からのサンプリングによる平均値を計算する必要があります。その方法の一つとして、マルコフ連鎖モンテカルロ法 (MCMC) が使われています。しかし、MCMCは初期状態から平衡状態への緩和に長時間の計算を要する場合があります。また、緩和した後も平均値を精度良く求めるための十分なサンプリング数の確保に時間がかかるといった課題もあります[1]。そこで本論文では、D-Waveマシンから得られる出力の分布がギブス・ボルツマン分布に近いことを利用して、平均値の計算にD-Waveマシンを用います。本手法により、手書き数字画像の生成・復元が可能であることに加え、ランダムなイジング模型も学習可能であることを示します。

本論文では、グラフ分割問題を取り扱う。グラフ分割問題とはグラフのノードを複数のグループに分割することであり、以下の二つの条件を満たすことを考える。

医療現場では人の命に関わる業務を行っているため、看護師の勤務の質が厳しく求められています。しかし、看護師の生活の質も守らなければいけないため、勤務表の作成が困難になっています。ナーススケジューリング問題 (Nurse scheduling Problem, NSP)とは、複数の制約の下で看護師に最適なシフトを割り当てる問題です。NSPは1969年以前より研究されており、NP困難であることが知られています。

CVRP (容量制約有りの配送計画問題)は、積載容量に制約のある車両で効率よく荷物を配送することを目的とした問題です。CVRPは、NP困難な問題であり、顧客の数が増えると組合せも爆発的に増加するため、全探索を用いて最適解を求めるには限界があります。そのため、古典的な手法では近似解を求めるのが主流です。この論文では、CVRPを小さな問題に分割し、量子アニーリングマシンと古典コンピュータの両方を用いたハイブリッドな手法を用いて解きます。そして、解の質や計算時間について古典的な手法との比較、および量子アニーリングマシン(D-Wave 2000Q)の性能の評価を行っています。

D-Wave Systemsによって開発が行われている量子アニーリングマシンは、組合せ最適化を高速に解くソルバーとして活発な分析が行われています。本論文では、渋滞解消を目的とした自動車の移動経路割当を組合せ最適化問題として定式化します。連続的な経路割当を実現するには最適化の高速性が求められるが、北京首都国際空港近辺における過去のドライブデータを用いてシミュレーションを行った結果、量子アニーリングは有効的な手法の一つであることを示しています。

本記事で紹介する論文では、D-Waveマシンを用いた量子アニーリングにより二値変数制約のついた 非負値行列分解 の手法と顔画像認識に応用した結果を示している。速度性能評価のために、古典的アルゴリズムを用いるGurobiと […]